同时确定钢纤维高强混凝土的断裂韧度及拉伸强度

管俊峰，鲁 猛，王 昊，姚贤华，李列列，张 敏

(华北水利水电大学土木与交通学院，河南，郑州 450045)

钢纤维在混凝土构件和结构中起抑制微裂缝扩展和阻滞宏观裂缝发展的关键作用[1-2]。钢纤维混凝土自身的宏观断裂参数，为衡量其抵抗裂缝起裂失稳的关键性能指标，与强度一样，为其重要的材料参数。而目前，对于断裂参数的确定，水工混凝土断裂试验规程(DL/T 5332-2005)[3]和美国材料与试验协会ASTM规范(E399-09)[4]，推荐测定钢纤维混凝土断裂韧度采用楔入劈拉法和三点弯曲法；而对于强度参数的测定，水工混凝土试验规程(SL 352-2006)[5]和澳大利亚国家标准(AS 1012.10-2000)[6]，推荐测定钢纤维混凝土拉伸强度分别采用棱柱状试件和圆柱状试件。可见，现有测试方法，对于钢纤维混凝土断裂韧度与拉伸强度的确定，须采用不同试件型式及试验方法。

大量试验研究表明[7-11]：实验室条件下小尺寸试件测试得到的钢纤维高强混凝土材料特性存在明显的尺寸效应。1)断裂韧度的尺寸效应。胡若邻等[7]对试件高度W=200mm、初始裂缝长度a0=60mm～100mm、韧带高度W-a0=100mm～140mm、最大骨料粒径dmax=25mm、钢纤维长度lf=30mm 的钢纤维高强混凝土试件进行断裂试验表明：直接由P-CMOD曲线确定的断裂韧性均随W-a0的变化而变化，具有明显的尺寸效应。徐平等[8 -9]对W=100 mm～300 mm、a0=5mm～150 mm、W-a0=30mm～200mm、dmax=20mm、lf=20mm 的钢纤维高强混凝土试件进行断裂试验表明：钢纤维混凝土的断裂参数随韧带高度W-a0的增加呈线性递减，随试件高度W的增加呈线性递增，表现出明显的尺寸效应。2)强度的尺寸效应。苏捷等[10]对W=70mm～150mm、dmax=20 mm、lf=25mm 的钢纤维高强混凝土试件，进行抗折强度试验，结果表明：抗折强度存在尺寸效应。江晨晖等[11]对试件高度W=50 mm～100 mm、直径Φ=50 mm～100mm、lf=12mm 的钢纤维高强混凝土试件进行抗压强度试验表明：随着试块尺寸增大，立方体抗压强度逐渐减小；随着试块直径增大，圆柱体抗压强度亦逐渐减小。

实验室条件下的钢纤维高强混凝土试件的韧带高度W-a0与钢纤维长度lf的比值约为(W-a0)/lf=1～10，试件高度W与骨料最大粒径dmax的比值约为W/dmax=5～20,从细观角度考虑，试件的相对尺寸(W-a0)/lf、W/dmax较小，试件的细观非均质性明显，钢纤维自身特性对钢纤维混凝土复合材料的宏观断裂的影响不能忽略。目前，对于确定钢纤维混凝土的断裂模型[12-15]，仍停留在宏观层面而未能从细观角度阐释钢纤维和骨料及其耦合对钢纤维混凝土断裂特性的定量影响机制，钢纤维特征参数也未体现在模型设计表达式中。更为重要的是，现有断裂韧度和拉伸强度仍需基于不同试验系统而需分别确定，而采用一种试件型式即可同时确定钢纤维混凝土断裂韧度和拉伸强度的应用模型还未见详细报道。

由此，本文考虑钢纤维高强混凝土类的复合材料的自身特性，将钢纤维掺量Vf、钢纤维长度lf、钢纤维直径df、钢纤维抗拉强度ff等纤维特征参数，引入到宏观断裂模型中，具体地将峰值荷载对应的虚拟裂缝扩展量Δafic与钢纤维的Vf、lf、df、ff、混凝土特征骨料di相联系，发展了由实验室条件下三点弯曲试件同时确定钢纤维高强混凝土无尺寸效应的断裂韧度KIC与拉伸强度ft、基于确定材料参数(KIC与ft)预测其结构个性化破坏的模型及其应用方法。

1 钢纤维高强混凝土的细观断裂模型

1.1 钢纤维高强混凝土断裂的细观影响机制

实验室条件下钢纤维高强混凝土相对尺寸(W-a0)/lf=1～10、W/dmax=5～20较小而非均质性明显。如图1所示，即使对相同尺寸试件(W和a0不变)，其细观层面上的钢纤维特性(Vf、lf、df、ff)、骨料颗粒(dmax、di)、试件边界(a0、W-a0)等互相影响，使得有限尺寸试件在宏观层面上表现出不同的结构特性。

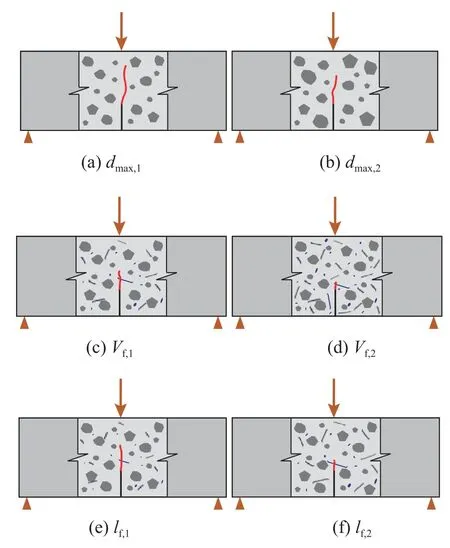
图1 钢纤维特性、骨料颗粒、试件边界的相互影响Fig.1 Interaction among steel fiber characteristics,aggregate particles and specimen boundary

对于普通混凝土，考虑骨料级配、试件前后边界等对断裂破坏的重要影响，课题组提出了考虑骨料级配的离散颗粒断裂模型[16-17]，基于小尺寸试件，即可同时确定普通混凝土的KIC和ft。而对于钢纤维高强混凝土复合材料，细观层面上，裂缝的扩展受钢纤维与混凝土骨料的耦合影响，两种作用不能忽略。由此，将钢纤维和骨料的耦合作用，体现到峰值荷载Pmax对应的虚拟裂缝扩展量Δafic的计算上，并将钢纤维特性(Vf、lf、df、ff)、骨料级配特性(di)与Δafic相联系，可得：

式中：Δafic虚拟裂缝扩展量，代表峰值荷载Pmax对应的初始裂缝尖端的裂缝扩展量；di骨料特征尺寸，代表起控制作用的骨料颗粒大小[16-17]，基于实际的粗骨料不同粒径分布、筛分曲线、试验筛孔等，可取为di=dmax、dav1、dav2、dmin等，dmax为粗骨料的骨料最大粒径，dmin为粗骨料的骨料最小粒径，dav1和dav2为dmax和dmin间的粒径大小，其具体数值的选取依赖于试验筛分曲线，其可视为不同骨料的平均粒径；n的取值依据如下，当试件韧带高度(W-a0)较大，若di取骨料最大粒径dmax时，仍不能满足相对尺寸(W-a0)/dmax≈10，则可取n=1,1.5,2,3,4,···，使得试件相对尺寸(W-a0)/ndmax≈10；a为试验系数，可通过大量试验的统计分析得出，本文基于试验结果的回归分析，a=3.5/10 000；Vf、lf、df、ff依次为钢纤维掺量、钢纤维长度、钢纤维直径、钢纤维抗拉强度等纤维特征参数。

图2阐述了钢纤维高强混凝土有限尺寸试件的裂缝细观断裂特性：为方便设计应用，真实Pmax时的虚拟裂缝扩展量Δafic如图2(a)，可简化为图2(b)所示的简化模型。其考虑了裂缝绕骨料或穿越骨料的跳跃性及不连续性扩展的特性，以及钢纤维存在对裂缝扩展的抑制作用，当相对尺寸(W-a0)/ndi≈10，(W-a0)/lf=1～10时，混凝土扩展的贡献为ndi，钢纤维阻裂的贡献为3.5/10 000Vflfffdf。本文通过试验分析，证明所发展模型计算方法的适用性与合理性。

图2 钢纤维高强混凝土虚拟裂缝扩展量Fig.2 Fictitiouscrack grow th length of steel fiber high-strength concrete

1.2 钢 纤 维高强 混 凝 土 材料 参 数与结 构 特性的联系

实验室条件下相对尺寸(W-a0)/lf、W/dmax较小的钢纤维高强混凝土试件应力分布如图3所示。

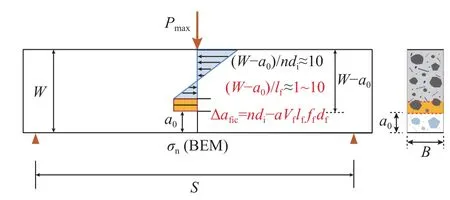
图3 考虑钢纤维作用的三点弯曲试件P max 时的应力分布Fig.3 Stress distribution at P max considering steel fiber for 3-p-b specimen

基于图3同时考虑钢纤维和骨料共同作用的虚拟裂缝扩展量Δafic的应力分布，可建立钢纤维高强混凝土相应的平衡方程，得出σn(Pmax,Δafic=ndiaVflfffdf)在Pmax时的解析表达式[18-25]：

式中，S为试件有效跨度。则基于边界效应理论，考虑钢纤维和骨料耦合作用的离散颗粒断裂模型的解析表达式为：

式中：a*∞为特征裂缝长度，为边界效应模型中的材料参数，其值由KIC和ft的交点得到[26-30]，；ae为考虑试件前后边界影响的等效裂缝长度，为几何参数，与试件尺寸与型式相关[18-25]，，其中，a0为初始裂缝长度，是指试件在浇筑时预留或对试件切割形成的裂缝长度，α 为试件缝高比α=a0/W，Y(α)为几何结构参数，对三点弯曲试件

变换式(3)形式可得：

如图4，基于发展的钢纤维高强混凝土离散颗粒断裂模型，可搭建起材料参数和结构特性的纽带桥梁：可由结构个性化特性来确定真实材料参数；可基于确定的材料参数来预测结构个性化破坏。

图4 钢纤维高强混凝土离散颗粒细观断裂模型Fig.4 Discrete particle meso fracture model of steel fiber high-strength concrete

1)确定材料参数。由式(2)确定σn(Pmax,Δafic=ndi-aVflfffdf)，计算确定ae，基于式(4)，通过数据拟合，即可外推同时确定出钢纤维高强混凝土的材料参数—断裂韧度KIC和拉伸强度ft。

2)预测结构破坏。若KIC与ft已确定，取不同的等效裂缝长度ae，则可基于式(2)，确定对应的σn(Pmax,Δafic=ndi-aVflfffdf)。进而建立钢纤维高强混凝土复合材料的完整破坏曲线。由图4可见，ae/＜0.1的区域，试件处于塑性状态，由拉伸强度控制；ae/＞10的区域，试件处于线弹性状态，由断裂韧度控制；0.1＜ae/＜10的区域，试件处于准脆性断裂状态，由拉伸强度和断裂韧度共同控制。在实验室条件下成型的试件一般处于准脆性断裂状态，试件的等效裂缝长度与特征裂缝长度的比值越接近10，则断裂韧度控制占比越高；ae/越接近0.1，拉伸强度控制占比越高。

2 试验验证

本文基于不同钢纤维特性、不同混凝土特性的试验，验证了所提模型和方法的合理性和适用性。

本文分析所用的具体钢纤维高强混凝土试件详见表1，均选用端钩形冷拉型钢纤维。所用MOUSAVI等[31]试验共计8种不同配合比，即水灰比w/c=0.24、0.35，每种w/c对应4种钢纤维掺量变化Vf=0%、0.2%、0.4%、0.6%，骨料最大粒径统一为dmax=12.5mm，每种配合比对应4 组试件，其试件高度W=40mm、80mm、160 mm、320mm。所用KAZEM I等[32]试验共4种不同配合比，w/c=0.4，每种w/c对应4种Vf=0%、0.2%、0.3%、0.4%，dmax=12.7 mm，每种配合比对应3组试件W=76.2 mm、152.4 mm、304.8 mm。MOUSAVI等[31]和KAZEM I等[32]均在万能试验机上进行三点弯曲试验，并按照RILEM FMT-89[33]的要求，以0.1mm/m in的恒定速率进行加载，试验中记录各试件的峰值荷载Pmax。此外，根据BSEN 12390[34]，对每个配合比进行立方体抗压强度试验，分别测得对应的fc，根据ASTM C496[35]，对每个配合比进行圆柱体劈裂抗拉强度试验，分别测得对应的fts。三点弯曲试件加载方式如图5所示。

图5 试件加载示意图[32]Fig.5 Schematic diagram of specimen loading

基于边长为100mm 的立方体抗压强度实测值fc，考虑混凝土抗拉强度约为其抗压强度的1/8～1/12[36]，同时考虑关系式ft=0.3，则拉伸强度预测值ft,p可确定出并列入表1。由尺寸效应模型(SEM)确定的断裂韧度见表1。

表1 钢纤维高强混凝土试件信息及材料特性Table 1 Details of steel fiber high-strength concrete specimensand material characteristics

2.1 确定w/c=0.24的钢纤维高强混凝土的K IC与f t

以MOUSAVI等[31]的w/c=0.24的钢纤维高强混凝土试件为分析对象。其试件的钢纤维特征参数lf=28 mm、df=0.4 mm、ff=1994 MPa，变化参数Vf取值分别为Vf=0.2%、0.4%、0.6%。所用混凝土粗骨料级配为4.75mm～9.5 mm、9.5mm～12.5mm[31]，则 分 析 确 定dmax=12.5 mm，dav=9.5 mm，dmin=4.75 mm。具体试件尺寸及实测试件峰值荷载Pmax见表2。

表2 w/c=0.24试件尺寸与实测P maxTable2 Detailed dimensionsof specimensw ith w/c=0.24 and experimental P max

基于本文所提模型，确定的w/c=0.24钢纤维高强混凝土的KIC与ft见图6及表3。由图6及表3可见：对于钢纤维高强混凝土，控制其相对尺寸(W-a0)/ndi≈10，采用本文所提公式Δafic=ndi-3.5/10 000Vflfffdf，确定KIC和ft的拟合曲线(式(4))具有较高的相关系数R2。

表3 w/c=0.24试件的Δa fic及确定曲线相关系数R2Table3 Δa fic of specimensand R2 of determination curve-fitting for w/c=0.24

图6 确定w/c=0.24的钢纤维高强混凝土的K IC 与f tFig.6 Determ ination of K IC and f t of steel fiber high-strength concrete w ith w/c=0.24

确定的w/c=0.24的钢纤维高强混凝土的KIC和ft，与拉伸强度预测值ft,p和SEM 确定值KIC,SEM(表1)吻合良好。

2.2 确定w/c=0.35的钢纤维高强混凝土的K IC与f t

以MOUSAVI等[31]的w/c=0.35的钢纤维高强混凝土试件为分析对象，钢纤维特征参数lf=28 mm、df=0.4mm、ff=1994MPa，Vf=0.2%、0.4%、0.6%。具体试件尺寸及实测Pmax可见表4。

表4 w/c=0.35的试件尺寸与实测P maxTable4 Detailed dimensionsof specimensw ith w/c=0.35 and experimental P max

基于本文所提模型与方法，确定的w/c=0.35钢纤维高强混凝土的KIC与ft如图7 及表5所示。

由图7及表5可见：对于w/c=0.35的钢纤维高强混凝土，采用所提模型，确定KIC和ft的拟合曲线(式(4))具有较高的相关系数R2。所确定w/c=0.35的KIC和ft，与拉伸强度预测值ft,p和SEM 确定值KIC,SEM(见表1)吻合良好。

表5 w/c=0.35试件的Δa fic及R2Table5 Δa fic of specimensand R2 for w/c=0.35

图7 确定w/c=0.35的钢纤维高强混凝土的K IC 与f tFig.7 Determ ination of K IC and f t of steel fiber high-strength concrete specimensw ith w/c=0.35

2.3 确定w/c=0.4的钢纤维高强混凝土的K IC 与f t

以KAZEM I等[32]的w/c=0.4的钢纤维高强混凝土试件为分析对象，其试件的钢纤维特征参数lf=36 mm、df=0.7 mm、ff=2100 MPa，变化参数Vf分别为Vf=0.2%、0.3%、0.4%。所用混凝土粗骨料级配为4.75 mm～9.5 mm～12.7mm[32]，则分析确定dmax=12.7 mm，dav=9.5 mm，dmin=4.75 mm。具体试件尺寸及实测试件峰值荷载Pmax见表6。

表6 w/c=0.4的试件尺寸与实测P maxTable6 Detailed dimensionsof specimens w ith w/c=0.4 and experimental P max

基于本文所提模型，确定的w/c=0.4钢纤维高强混凝土的KIC与ft如图8及表7所示。可见：确定KIC和ft的拟合曲线(式(4))具有较高的相关系数R2。所确定的w/c=0.4的钢纤维高强混凝土的KIC和ft，与拉伸强度预测值ft,p和SEM确定值KIC,SEM(见表1)吻合良好。

表7 w/c=0.4试件的Δa fic 及R2Table7 Δa fic of specimensand R2 for w/c=0.4

由图6～图8可知，对于钢纤维高强混凝土，控制相对尺寸(W-a0)/ndi≈10，采用所提虚拟裂缝扩展量的计算方法Δafic=ndi-3.5/10 000Vflfffdf，确定的不同钢纤维特性、不同混凝土特性的钢纤维高强混凝土断裂韧度KIC与拉伸强度ft均与拉伸强度预测值ft,p和SEM 确定值KIC,SEM(见表1)吻合良好。证明所发展模型计算方法的适用性与合理性。

图8 确定w/c=0.4钢纤维高强混凝土的K IC 与f tFig.8 Determ ination of K IC and f t of steel fiber high-strength concrete specimens w ith w/c=0.4

2.4 模型特例验证

以未掺纤维的高强混凝土为研究对象，即Vf=0%，则虚拟裂缝扩展量的计算公式Δafic=ndi-3.5/10 000Vflfffdf蜕化为：Δafic=ndi。

基于MOUSAVI 等[31]的w/c分别为0.24、0.35和KAZEM I等[32]的w/c=0.4，Vf=0%的高强混凝土的试验结果，采用本文所提模型，确定Vf=0%高强混凝土的KIC与ft如图9所示。

由图9可见：对于Vf=0%的高强混凝土，控制(W-a0)/ndi≈10，Δafic=ndi，确定KIC和ft具有较高的相关系数R2。所确定的高强混凝土的KIC和ft，与拉伸强度预测值ft,p和SEM确定值KIC,SEM(表1)亦吻合良好。

3 材料参数与结构特性的关系曲线

若材料断裂韧度KIC与拉伸强度ft已确定，则可基于式(1)～式(4)构建出钢纤维高强混凝土材料参数(KIC和ft)与结构特性(σn或Pmax)的关系全曲线。

图10～图13为基于确定的KIC和ft，分别建立的不同钢纤维特性和混凝土特性的混凝土断裂设计曲线。当给出任意构件或结构的几何参数ae，即可由破坏设计曲线确定出其相应的结构特性Pmax(Pmax由σn反解出)。

图10 构建w/c=0.24的钢纤维高强混凝土断裂破坏曲线Fig.10 Fracture curvesof steel fiber high-strength concrete w ith w/c=0.24

图11 构建w/c=0.35的钢纤维高强混凝土断裂破坏曲线Fig.11 Fracture curvesof steel fiber high-strength concrete w ith w/c=0.35

图12 构建w/c=0.4的钢纤维高强混凝土断裂破坏曲线Fig.12 Fracture curvesof steel fiber high-strength concrete w ith w/c=0.4

图13 构建V f=0%的高强混凝土断裂破坏全曲线Fig.13 Fracture curvesof steel fiber high-strength concrete w ith V f=0%

试样浇筑与养护条件，钢纤维与骨料分布的随机性等，都会对试验结果产生影响；混凝土裂缝随机性、离散性及个性差异特征是其固有属性。如图10～图12所示，考虑裂缝扩展的随机性，引起试验数据的离散性，引入破坏曲线的上下限。试验结果表明：断裂破坏全曲线的±20%即可涵盖全部试验数据(图10～图12)。设计曲线上下线与混凝土自身的材料特性密切相关，受其细观层面骨料与纤维性能、分布等的具体影响，因此是其材料个性化特性的真实定量反映。

由已知的材料参数KIC和ft可确定另一个描述材料所属破坏状态的材料参数。由ae≥10得出相应的ae理论值，即可确定出不同缝高比α 对应的满足线弹性断裂的最小试件尺寸Wmin。由图10～图12可见，具有不同钢纤维特性和混凝土特性的钢纤维高强混凝土，都处于准脆性断裂状态，即使最大尺寸试件W=320mm、W=304.8mm，也未达到线弹性状态。基于全曲线确定的满足线弹性状态的钢纤维高强混凝土的理论最小尺寸Wmin如表8所示。

由确定的材料参数KIC和ft，建立Vf=0时高强混凝土的断裂全曲线见图13。

如图13所示：所建立的模型特例Vf=0时的断裂破坏全曲线，其±20%可涵盖全部试验数据。分析所用的高强混凝土试件处于准脆性断裂状态；即使最大尺寸试件W=320mm、W=304.8mm 也未达到线弹性状态。基于全曲线确定的满足线弹性状态的钢纤维高强混凝土的理论最小尺寸Wmin如表8所示。

表8 不同类型混凝土满足线弹性状态的理论最小尺寸W minTable8 Theoretical m inimum size W min of different typesof concrete satisfying linear elastic state

4 结论

本文考虑钢纤维特性和骨料性能对断裂破坏的耦合影响，发展了同时确定钢纤维高强混凝土的断裂参数与拉伸强度的细观断裂模型及应用方法。通过钢纤维掺量、水灰比等变化的12种配合比的钢纤维高强混凝土试验，验证了所发展模型和方法的合理性与适用性。基于本文所提模型确定的材料参数KIC和ft，进一步建立起钢纤维高强混凝土材料参数与结构特性的关系曲线，从而为钢纤维混凝土断裂性能的设计提供了科研依据。研究得到具体结论如下：

(1)将钢纤维特性参数：钢纤维掺量Vf、钢纤维长度lf、钢纤维直径df及钢纤维抗拉强度ff，和混凝土骨料特征参数di,引入钢纤维高强混凝土有限尺寸试件峰值荷载Pmax时虚拟裂缝扩展量Δafic的具体计算公式。

通过本文详细分析，对于钢纤维高强混凝土，控制其相对尺寸(W-a0)/ndi≈10，虚拟裂缝扩展量可由Δafic=ndi-3.5/10 000Vflfffdf计算，则分别确定出12种配合比的钢纤维高强混凝土的断裂韧度KIC与拉伸强度ft，都与拉伸强度预测值ft,p和SEM 确定值KIC,SEM吻合良好。

(2)基于确定的KIC和ft，可分别建立起描述钢纤维高强混凝土材料的强度—准脆性断裂—断裂韧度控制的断裂破坏设计全曲线。考虑混凝土试验的离散性为其固有属性的事实，所建立设计曲线的±20%，可解释钢纤维高强混凝土试验数据的随机性，即曲线可涵盖高强钢纤维混凝土的全部试验数据。

(3)对于模型特例Vf=0%的高强混凝土，虚拟裂缝扩展量的计算方法统一公式可蜕化为特例型式：Δafic=ndi，采用其确定的KIC和ft，亦与ft,p和KIC,SEM吻合良好。建立全曲线的±20%可涵盖全部试验数据。

本文研究为由细观层面的钢纤维特性和骨料特性的改变，来控制宏观层面的材料性能设计等方面，提供了新思路。本文研究针对配置端钩形冷拉型钢纤维的钢纤维高强混凝土。今后，将进行确定配置其他类型钢纤维的钢纤维混凝土断裂韧度与拉伸强度的研究。