微小荧光测温探头热响应过程非稳态传热特性分析

陈 伟， 白万栋， 牛家宏， 吴 锋， 张 雁

(1. 四川大学空天科学与工程学院，四川 成都 610065; 2. 中国航发四川燃气涡轮研究院，四川 绵阳 621703)

0 引 言

在航空发动机非稳态试验过程中，流场介质温度变化的测量是评判发动机性能状态，分析发动机子系统、零部件非稳态工作特性的重要依据[1-2]。但与此同时，精确测量流体介质温度动态变化过程，一直也是发动机非稳态试验测试中的难点之一[3-4]。在常规接触式温度传感器测温过程中，由于自身热容，以及流体和固体传热速率的差异，传感器需要一定的时间才能与被测介质达到热平衡，即响应时间[5-6]。其动态响应特性既与传感器自身结构设计有关，也与所测介质及周围环境有关[7-8]。

荧光测温是近年来科研人员广泛关注的一种非接触式光学测温技术[9-11]，具有分辨率高、响应时间快的特点，在非稳态温度测量中具有良好应用前景。其基本原理是，荧光材料受到一定能量的光激发将发出荧光，当激励光停止时，荧光的发光持续时间取决于激发态寿命。同时，在特定温度范围内，荧光衰减时间和荧光强度会表现出一定的温度相关性[12]。通过建立某个受温度影响的荧光参数（如荧光强度）与温度的对应关系，即可实现温度测量[13]。

根据测温范围，可选择不同的荧光材料。现有成熟荧光材料主要有：Y2O3、Al2O3、YSZ、YAG 等。在使用过程中，需采用物理气相沉积(PVD)、化学气相沉积(CVD)或溶胶-凝胶法(Solegel)等工艺将荧光材料呈膜状制备于物体表面上[14]。由于荧光材料的导热系数相对金属材料普遍较低，其产生的热阻效应，将会改变荧光材料涂层及其所依附基体表面的热惯性，进而影响荧光测温的动态响应特性[15]。

基于以上背景，本文针对某微小型荧光测温探头的非稳态传热问题，采用理论分析与数值计算相结合的方法，研究了该荧光测温探头随主流温度变化的热响应过程，探讨了基座结构及材料、荧光材料涂层厚度等因素对荧光测温探头非稳态传热特性的影响规律，为荧光测温技术在航空发动机非稳态试验中的应用提供参考。

1 数值计算方法

1.1 物理模型

本文所研究的微小荧光测温探头结构如图1所示，其主要由基座和荧光涂层所组成。基座的球头部分直径为 φ=0.5～2 mm，支杆部分直径为d=0.3 mm，长度为L=10 mm；荧光材料涂层仅喷涂在球头区域，厚度 δ=0.01～0.1 mm，其主要成分为Al2O3，导热系数 λAl2O3=35 W/(m·K)，比热容CpAl2O3=750 J/(kg·K)，探讨了两种基座材料的传热特性，分别为：金属铜，导热系数 λCu=401 W/(m·K)，比热容CpCu=385 J/(kg·K)；陶瓷材料，导热系数 λcer=0.65 W/(m·K)，比热容Cpcer=800 J/(kg·K)。

图1 微小荧光测温探头在流道中的物理模型示意图

微小荧光测温探头处于直径D=100 mm的流道中心，通过支杆固定于流道壁面。流体介质为空气，进口流速V=200 m/s，出口背压为P=300 kPa。为研究探头的热响应过程，进口主流温度发生突变，温度变化速率为1 000 K/s，在时刻0～0.2 s内，进口温度由300 K线性上升到500 K，之后保持500 K不变。

1.2 数值计算方法及网格

考虑到微小荧光测温探头在流道中的流动传热分布具有很强的对称性，本文将其简化为二维流动传热问题，并采用非定常流热耦合数值计算方法，研究探头在热响应过程中的非稳态传热特性。计算中，为减小流道壁面及其边界层流动对测温探头非稳态传热的影响，探头支杆与流道壁面未接触，且流道壁面设置为绝热条件。非定常流热耦合数值计算基于ANSYS CFX程序进行，流体区域求解三维非定常粘性的雷诺平均N-S方程。数值方法采用时间追赶的有限体积法，空间离散采用中心差分，时间离散应用四阶龙格-库塔方法。湍流模型采用SST模型，近壁面处理方法采用自动壁面函数法。

计算域采用结构化网格进行划分，计算网格如图2所示。为开展非定常流热耦合数值计算，在垂直纸面的高度方向拉伸了5层网格。为更精细地得到涂层内的温度分布，涂层内部（固体）也划分了网格进行耦合求解。在进行数值计算前，针对球头部分直径为φ=2 mm，涂层厚度为δ=0.1 mm探头的热响应过程，采用了5种尺度的计算网格进行网格无关解验证，5种网格总数分别为1.2万、4.5万、8.8万、12.5万、25万。球头部分中心点的温度变化曲线对比如图3所示，可以看出，不同网格尺度的计算结果相差并不大，主要的差别体现在温度迅速升高的非稳定阶段。当球头温度稳定后，不同网格计算出的温度基本一致。

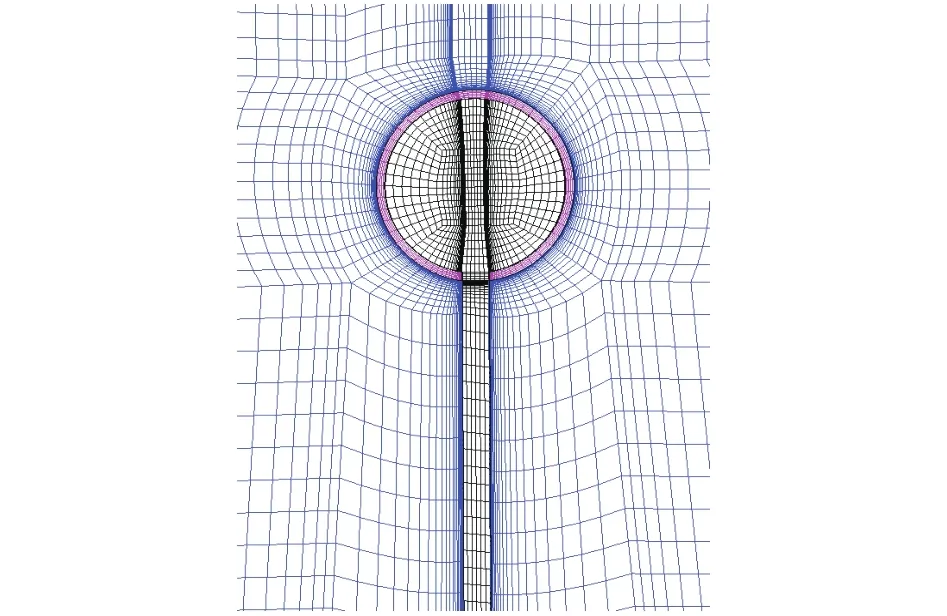
图2 探头附近数值计算网格局部视图

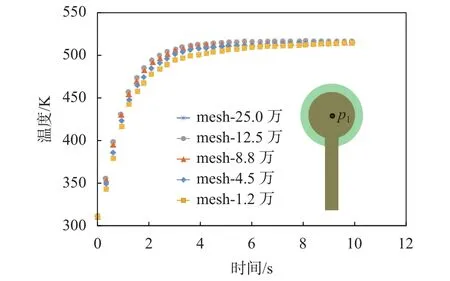
图3 不同网格尺度的探头中心点温度变化

为了便于比较不同网格计算结果的差异性，定义不同数值结果之间的相差系数ψ：

式中：Tend——流场进口最终静温500 K；

Tstr——流场进口初始静温300 K；

ΔT——两种结果特征点在同一时刻的温度差。

以8.8万网格的计算结果为参考，其与12.5万、25万网格的最大相差系数分别为0.5%、0.8%，该计算精度满足本文分析要求。因此，后续计算中均采用8.8万的网格进行计算。

2 计算结果分析

2.1 探头温度分布随时间的变化

图4给出的是球头直径d=2 mm，涂层厚度δ=0.1 mm，基座材料为铜的探头，在热响应过程中不同时刻的内部温度分布云图。可以看到，当主流温度在0.2 s内由300 K变化到500 K的过程中，探头温度仅由314 K上升到332 K ～358.5 K，其中球头部分的温度均低于340 K。探头温度变化明显滞后于主流温度变化，直到第5.0 s时，探头基座温度才基本达到稳定状态。需要说明的是，进入稳定状态后，探头温度比主流温度高，这是由于探头感受的是介于主流总温与静温之间的温度。另一方面，支杆部分的温升明显快于球头部分。这是由于，相比材料铜而言，球头区域的荧光涂层导热系数低，热阻大，温升速率低。当主流温度升高时，支杆温度首先变化，并在温差作用下，有部分热量从支杆向球头区域传递。

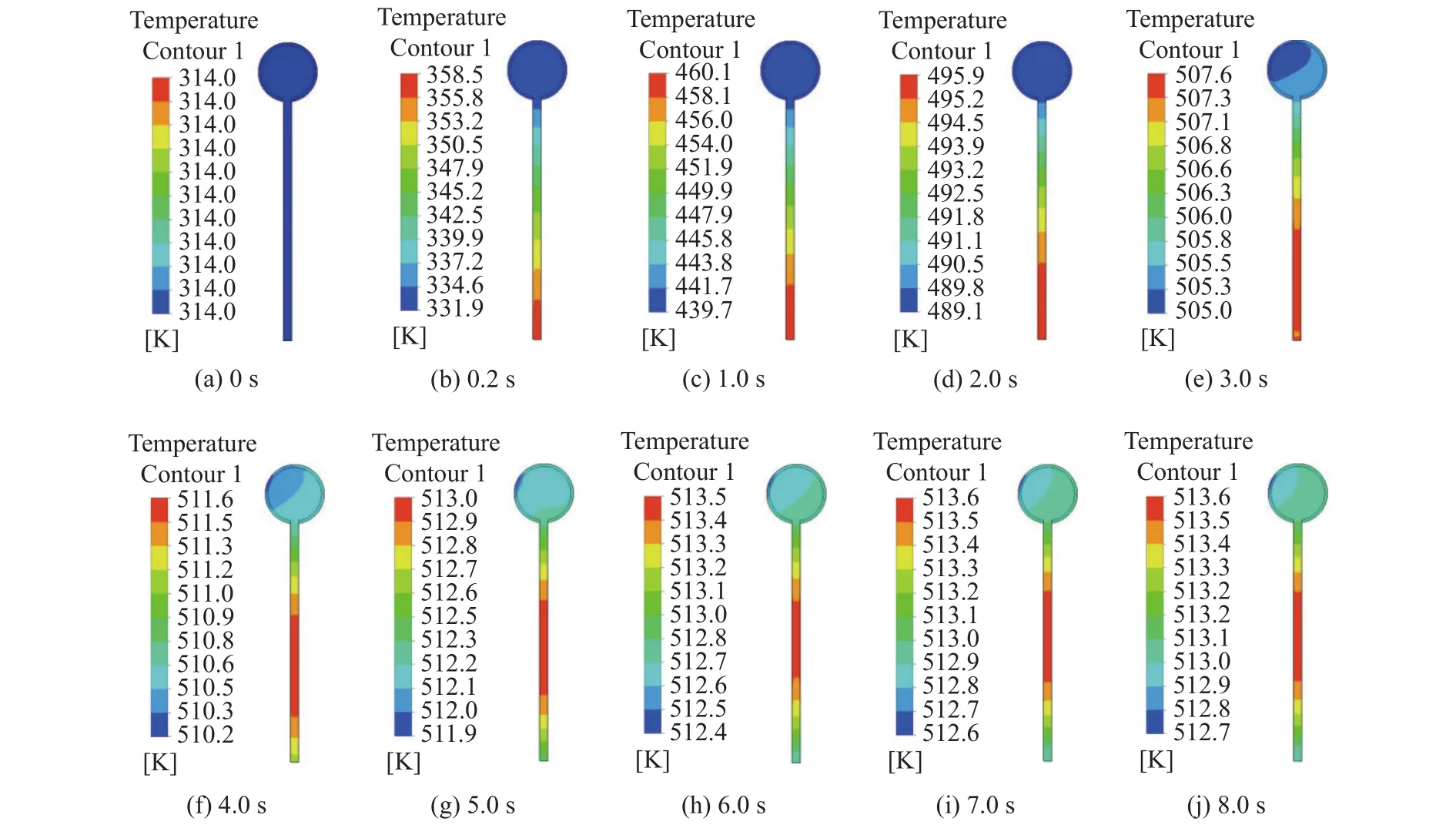
图4 探头在热响应过程中不同时刻的温度分布(d=2 mm, δ=0.1 mm, 基座材料:铜)

为更清晰地观测探头各处的温度变化趋势，选取了探头5个特征位置，来表达其温度随时间的变化规律。5个特征位置如图5和表1所示。

表1 探头5个特征位置说明

图5 所选取的探头5个特征位置示意图

当主流温度突变时，探头各特征位置处的温度随时间的变化关系如图6所示。对比可见，除了探头支杆区域的p5点温升速度略快外，探头球头区域的各点温度变化差异极小，反映出探头球头区域的温度变化整体是均匀的。

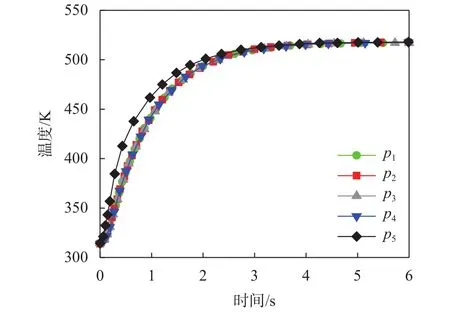
图6 探头各特征位置处温度随时间的典型变化

2.2 探头直径和荧光涂层厚度的影响

本节对比分析了探头直径和荧光涂层厚度对探头非稳态传热特性的影响。探头直径的变化范围为0.5～2.0 mm，荧光涂层的厚度范围为0～0.1 mm，基座材料为铜。计算方法均采用非定常流热耦合数值计算。在分析探头直径的影响时，保持荧光涂层厚度不变。以“探头直径-涂层厚度”的方式区分，如“2.0 mm-0.1 mm”表示直径为2.0 mm、荧光涂层厚度为0.1 mm的探头。

图7 比较了“2.0 mm-0.1 mm”、“1.5 mm-0.1 mm” 、“1 mm-0.1 mm”、“0.5 mm-0.1 mm”四种直径探头结构的非稳态传热特性。以探头中心的p1点温度变化曲线为例，从图中可以看出，“2.0 mm-0.1 mm”探头p1点的温度上升速率最慢，随着探头直径的减小，p1点温度上升速率有所加快，这主要是由于探头直径越小，基座自身的导热热阻越小，热响应越快。p1点的温度变化是探头表面换热和内部导热共同作用的结果，这说明探头直径是影响特征点温度响应的重要因素。

图7 不同直径探头p1点的温度变化

探头表面的荧光涂层通常较薄（＜0.1 mm），但涂层的导热系数相对较小。为评估涂层的影响，分别计算了不同涂层厚度条件下，探头的非稳态传热特性，如图8所示。可以看到，本文所研究的荧光涂层热阻对探头温度变化的影响较小。随着涂层厚度的减小，探头中心的p1点的温度变化响应略有加速，但是幅度不大。同时可以看到，当涂层厚度从0.01 mm变化为无涂层时，典型特征点p1的温度曲线基本无变化。这是由于，在非稳态传热过程中，由于基座导热系数大，支杆对球头区域的导热起到了主要作用。随着荧光涂层厚度的减薄，球头区域的涂层热阻减小，但基座导热热阻依然存在，且与支杆到球头的导热热阻相当，因此荧光涂层厚度改变对球头中心处的温度变化过程影响不大。

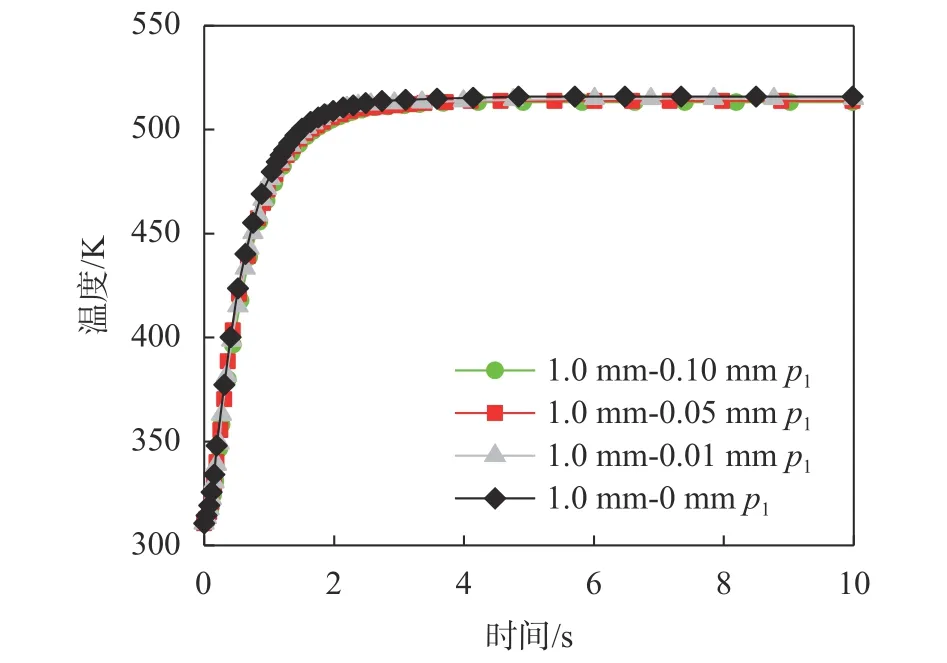
图8 不同荧光涂层厚度下探头p1点温度变化

2.3 探头基座材料对非稳态传热性能的影响

为研究基座材料对探头非稳态传热特性的影响，本节采用非定常流热耦合方法，对直径2 mm，涂层厚度0.1 mm的探头进行对比分析。

各特征位置处的温度变化曲线如图9所示，其中（a）探头基座材料为铜，（b）探头基座材料为陶瓷。从图中可以看到，采用陶瓷基座后，各特征位置的温度响应要比采用铜基座的温度响应缓慢得多。陶瓷基座的探头大概在25 s后，各特征位置的温度分布才达到稳定状态。

图9 “2.0 mm-0.1 mm”探头特征位置的温度变化

表2给出的是在热响应过程中，探头各个特征位置点的温度达到480 K所用的时间对比。从表中可以看出，铜基座的探头p1、p2、p3、p4点达到480 K的时间是相同的，反映出探头内部温度分布非常均匀。这是因为铜基座的导热系数高，内部热阻小，探头感受外流体的温度变化主要受表面对流换热热阻的作用。而陶瓷基座的探头各特征位置点达到480 K的时间比铜基座探头要缓慢得多，这是由于陶瓷基座的导热系数很低、内部热阻大，导热热阻已经与对流换热的热阻相当，所以探头各特征点达到480 K的时间均不相同。p1点到达时间比p2、p3、p4点延迟3 s左右，这是由于热量从p2、p3、p4点传导到p1点需要经过探头内部的导热过程，这个时间差说明探头内部的导热热阻已经十分显著，是影响探头内部温度分布的一个重要因素。另一方面，p2、p3、p4点到达480 K的时间也略有不同，这主要是由于这三点外侧的流场和对流换热系数不同所造成的。

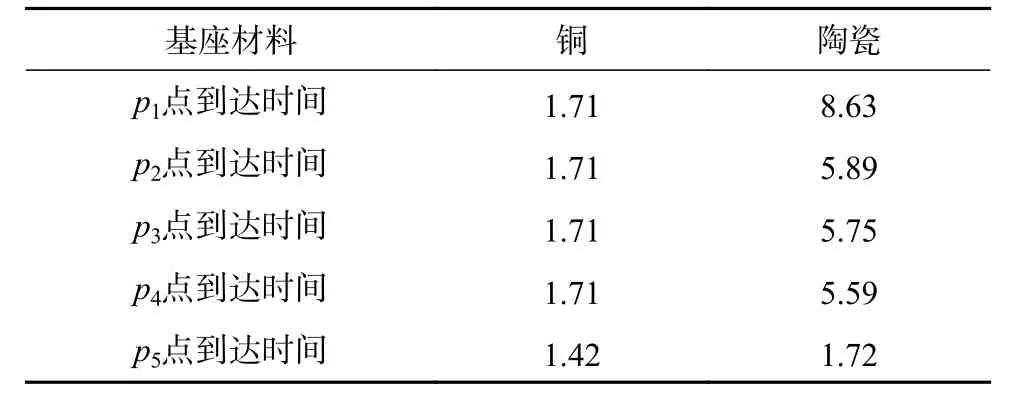
表2 探头各特征位置点达到480 K的时间对比s

2.4 探头的一维传热分析

图10为探头传热的一维热阻分析图。热量从外部流场进入探头中心需要经过三段热阻，其中R1为表面的对流换热热阻，R2为荧光涂层材料的导热热阻，R3为基座材料的导热热阻。从流热耦合数值计算结果中，可以得到探头表面的平均换热系数约为1 000 W/(m·K)，取荧光涂层最大厚度为0.1 mm，涂层导热系数为35 W/(m·K)。基座材料为铜时，导热系数为401 W/(m·K)，厚度取最大厚度1 mm。基座材料为陶瓷时，导热系数为0.65 W/(m·K)，厚度取最大厚度1 mm，分别计算四种热阻。

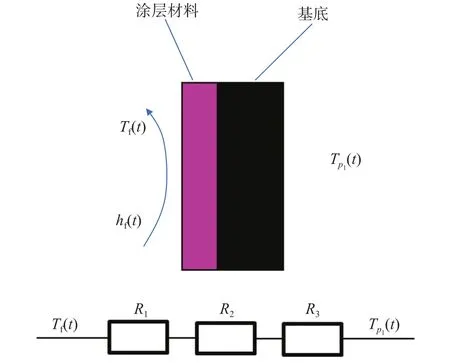
图10 探头传热的一维热阻分析

从以上计算可以看出，R2与R3铜远远小于R1，约小3个数量级。因此，铜基座材料探头的传热过程，主要热阻为表面对流换热热阻，而R2与R3铜可以忽略不计。也就是说，在铜基座材料的探头结构中，可以认为荧光涂层和基座为超导热体。但是，陶瓷材料基座的导热热阻R3陶瓷与R1相当，因此，陶瓷基座的探头表面对流换热热阻与内部导热热阻都是不可忽略的，探头内部的温度分布受表面对流换热热阻和导热热阻的共同作用。

从一维传热分析可以看出，对于铜基座的探头，在探头直径不变的情况下，荧光涂层厚度对探头温度响应的影响很小，而陶瓷基座的探头内部温度分布除受到表面对流换热影响外，内部导热热阻不可忽略，这与非定常流热耦合数值分析的结论是一致的。

3 结束语

针对荧光测温技术在航空发动机非稳态试验测量中的应用，本文采用理论分析和非定常流热耦合数值计算相结合的方法，研究了某微小型荧光测温探头在热响应过程中的非稳态传热特性。主要结论如下：

1）采用陶瓷材料的探头温度响应速率明显低于铜基座材料。同时，荧光涂层温度达到稳定状态需要基座也达到稳定状态。

2）探头内部的温度响应速率随探头直径的减小而加快，直径越小，导热热阻越小。探头直径是影响探头温度响应时间的重要因素。

3）铜基座探头内部的温度响应速率随荧光涂层厚度的变化不明显。

4）铜基座探头内部温度主要受表面对流换热热阻的影响，而内部导热热阻的影响很小；陶瓷基座材料的探头内部温度受到表面对流换热热阻和内部导热热阻的共同作用，且两者的热阻相当，都不可忽略。