基于结构性能的大型贮液箱最优维护时机确定

陈 媛， 周志杰， 明志超， 王 杰， 张 亮

(1. 火箭军工程大学导弹工程学院，陕西 西安 710025; 2. 战略支援部队航天系统部装备部装备保障队，北京 100094)

0 引 言

近年来，液体贮箱的体积持续增大，建设大型贮液箱已成为必然趋势[1]。大型贮液箱（large liquid tanks, LLT）作为重要贮藏载体，通常用来存放大量有毒的易燃易爆液体。同时，LLT长期在严峻的生产环境中运行，会加速LLT的结构性能的劣化，导致罐体变形，进而增大了罐体泄漏、火灾、爆炸等事故发生的风险[2-3]。为确保LLT能够安全可靠地储液，当LLT运行到一定时间后需要对其结构进行预防性维修。然而，若维修周期过短，则会增加LLT系统维修停机时间和维修费用，降低设备利用率；若维修周期过长，则无法及时发现LLT系统的安全隐患，增加故障发生次数[4]。因此，如何为LLT系统确定最优维护时机，是目前亟待解决的问题。

目前，常用确定最优维护时机的方法可分为基于统计或可靠性分析的方法和基于RBI（rist based inspection）方法。一方面，基于统计或可靠性的方法，是通过分析失效机理确定系统剩余寿命，或是利用概率理论求出系统可靠度，来确定维修时机。例如，文献[5]在分析储油罐失效机理基础上建立系统可靠性模型，并以单位时间最小费用为目标，确定了储油罐的最佳维修时机。文献[6]基于Gumbel极值分布建立剩余寿命预测模型，并预测当可靠度为0.999 9时某油库储罐的剩余寿命为17年，以此确定下一次开罐检修时机应大于10年。另一方面，基于RBI方法，主要通过准确的风险评估与风险可接受值相比较来确定维修时机，使得在保证系统安全运行下也能降低检测费用。例如，文献[7]提出了基于RBI的检修周期确定方法，并认为当某油库储油罐可接受的风险值为3.54×104时，其检修周期应大于8年。文献[8]基于RBI方法，将苯乙烯、乙苯等3套装置的承压类特种设备首次维修时机从2018年延期至2020年，大幅提高企业经济效益。

对于典型的长寿命、高可靠的复杂系统，LLT具有如下特性：1）LLT系统所能获取的有价值先验信息较少，即系统失效时的故障数据以及专家经验匮乏；2）由于LLT的工作环境复杂多变，导致监测数据不完全可靠；3）在确定LLT最优维护时机时需要处理包括定性资料和定量故障数据等半定量信息。综上所述，上述所提两种维修周期确定方法在面临先验信息缺乏时，往往难以建立准确的维修时机决策模型。而LLT的结构性能状态通常会受到贮箱的贮液量、不均匀沉降等多个指标影响，因此如果能够有效预判LLT系统未来时刻的多个指标状态，并对未来时刻的LLT系统结构性能状态进行评估。依据评估结果，在保证系统稳定的前提下，进而确定LLT的最优维护时机。这样不仅能够减少维护成本提高系统经济性，也能预防系统故障的发生从而提高系统可用性。

维纳过程[4]作为一种经典的预测方法，能够依据现有指标监测数据获取设备未来时地刻的状态信息，为最优维护时机的确定提供数据支撑。此外，置信规则库[9]（belief rule base, BRB）模型，不仅能够提供一种灵活方式描述半定量信息，也能借助证据推理（evidential reasoning, ER）算法有效处理半定量信息从而得出准确可靠的评估结果。目前，BRB在复杂系统安全性评估领域表现良好[10-11]。然而，由于LLT系统存在先验信息匮乏且监测数据不完全可靠问题，导致BRB模型参数的准确估计成为了困难。

鉴于此，本文提出一种基于结构性能状态的大型贮液箱最优维护时机确定方法。首先，借助维纳过程预测方法，获取LLT系统监测指标在未来时刻的状态。其次，对BRB模型进行改进，构建了一种基于有限元法并考虑属性可靠度的置信规则库（the finite element method and belief rule base with attribute reliability, FEM-BRB-r）评估模型，实现在先验信息不足且监测数据受到扰动情况下LLT未来时刻的结构性能状态评估。最后，依据单位时间的最小维护成本与最低工作结构性能状态确定最优维护周期，并进行实验验证。

1 基于结构性能的大型贮液箱最优维护时机确定方法

1.1 基于维纳过程的指标预测方法

在LLT系统的最优维护时机确定中，需要通过函数预测LLT系统未来时刻的指标状态情况，为最优维护时机的确定提供数据支撑。本文基于维纳过程构建LLT系统的指标性能状态预测模型，维纳预测公式可以表示为[4]：

式中：xi(t+Δt)——第i个监测指标在 (t+Δt)时刻对应的状态；

xi(t)——第i个监测指标在t时刻的指标状态；

λ——退化系数；

ξ——扩散系数；

Δt——预测间隔长度，最大间隔为a；

B(Δt)——服从标准正态分布的布朗运动，即B(Δt)～ N(0,Δt)。

1.2 基于FEM-BRB-r模型的LLT结构性能状态评估

1.2.1 评估模型的构建

有限元法[12-13]（finite element method, FEM）作为结构力学中最广泛的计算分析方法，可以对建立的机理仿真模型实现在特定工况下的结构力学分析，从而得到结构变形规律。为弥补知识、数据有限情况下的规则库构建困难问题，可借助有限元方法实现LLT结构力学分析并获取不同工况下的结构变形规律，为置信规则库的构建提供支持。具体步骤如下：

1） 指标参考值及工况的确定

通过机理分析，选定ｍ个关键载荷指标，即X={x1,···,xm}，并将作用于LLT的各载荷指标形成的合力矢量记做f=(x1,···,xm)。各载荷指标对应的参考值A={Ai;i=1,···,m}可以根据行业标准确定。为实现评估模型参数的估计，基于指标参考值的数量，专家设计了与置信规则库对应的L种工况，其中。

2）基于有限元法的结构静力学分析

为分析Ｌ种工况下的LLT结构性能状态，通过施加不同的合力矢量fj(j=1,···,L)，借助有限元方法得到对应的种工况下的整体结构最大变形量w={wj,j=1,···,L}。其中，第j种工况下的整体结构最大变形量wj(j=1,···,L)，计算公式如下：

式中：Ｋ——整体刚度矩阵；

b——整体结构变形向量，且wj=max(b)；

f=(x1,···,xm)对应第j种工况下的载荷指标的合力矢量；最后，采用min-max标准化方法对最大变形量w={wj,j=1,···,L}进行线性变换，得到归一化后的最大变形量，以提高模型处理数据的能力，具体计算方法参考文献[14]。

3） 置信规则库的构建

首先，专家初始化规则权重 θk(k=1,···,L)和属性权重 δi(i=1,···,m)，并将结构性能状态作为评估模型的输出，用于衡量当前整体结构最大变形量对结构性能的影响，分别为好、中、差、极差四个等级即评估结果可以表示D={Dn;n=1,···,4}。其中，结构性能状态等级参考值 μ (Dn)以及在各个结构性能状态等级下结构变形量对应的参考值 μ (DSn)，如表1所示。

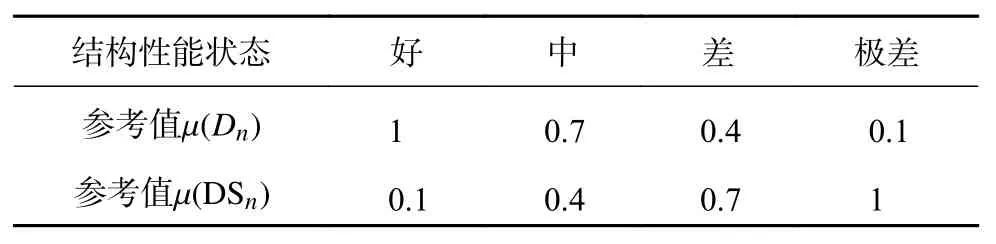
表1 石油储罐结构性能状态参考等级和参考值

式中： μ (DSn)——第n个 评估结果Dn下结构变形量对应的参考值；

N——评估结果个数；

然后，采用信息一致性的方法[15]，计算得到第i个载荷指标的属性可靠度：

式中：xi(t)——第i个载荷指标的第t个观测；

T——观测数据的个数；

最后，基于上述所获得的模型参数与计算得到载荷指标的属性可靠度相结合，根据规则确定初始置信规则库，完成FEM-BRB-r评估模型的构建。其中，第k条规则表示如下：

1.2.2 评估模型的推理

当FEM-BRB-r评估模型建立后，其所包含的知识库可用来对给定输入进行推理，具体如下：

1)当监测数据可用时，与初始置信度计算方法一样，采用基于效用的转化方法，求取输入指标xi相对于第j个参考值Ai的匹配程度。

2)不同的输入能够激活相对应的规则。激活权重zk可由下式计算得到：

参数hi(i=1,···,m)——融合因子，描述了属性权重和属性可靠度的共同影响；

当载荷指标完全可靠，此时ri=1，hi=δi，FEMBRB-r模型退化为BRB模型；当载荷指标不完全可靠时，ri＜1，则hi＜1。

3)为提高模型处理不确定性的能力，使用ER算法来聚合被激活的规则：

4)在融合L条规则后，模型最终的输出结果可以表示为：

式中：y——评估模型的输出，表示当前贮箱结构性能状态；

μ(Dj)——第j个评估结果对应的参考值。

1.3 大型贮液箱最优维护时机的确定策略

基于评估结果，本节详细描述最优维护时机确定策略[16]：

首先，结合机理知识，专家确定LLT系统的维护等级Ee(e=1,···,v)以及第e个维护等级下对应的参考值ye（y1≥ye≥yv） 、维护措施M(Ee)以及维护费用qe。

其次，在保证系统最低结构性能状态的前提下，达到单位时间内的平均维护成本最小。假设系统从t时刻运行至(t+Δt),Δt=1,···,a时刻，此时的系统结构性能状态为y(t+Δt)，则最优维护时机Tbest计 算如下：

式中：c(t)——单位时间的平均维护费用；

qe——进行第e种维护措施所对应的维护成本；

pe——进行第e种维护措施所发生的概率。

由公式（12）计算得到。当y(t+Δt)＞yε时，表示系统运行到 (t+Δt)时刻时，对应的系统结构性能状态要大于最低结构性能状态阈值yε。此时，依据公式（11），可以确定当前单位时间内维护费用最低时所对应的时刻，即为最优测试时刻；当y(t+Δt)≤yε，系统的结构性能状态达到甚至低于最低的结构性能状态阈值，此时时刻即为最优测试时刻，系统必须停止运行并进行检查与维修。

2 实例研究

石油储罐作为一种典型薄壁圆柱体，储罐的不均匀沉降以及液面高度因素最能反映石油储罐的结构性能状态，常被当作评估指标用于石油储罐的结构安全性评估[17]。

为验证所提方法的有效性，以体积为50 000 m3容量的大型石油储罐为例，选用不均匀沉降以及液面高度作为监测指标，进行最优维护时机确定的研究。实验采用静力水准仪以及液位传感器，收集了2012-2019年间，储罐从墙体浇筑阶段到正常贮存状态下的不均匀沉降和液面高度指标观测数据。其中，采样频率为一年两至三次，实验共获得19组样本。

2.1 基于维纳过程的指标预测方法

为了验证所提方法能够弥补先验信息缺失问题，基于19组和15组指标监测数据设计了两组实验，来模拟先验信息完全和缺失情况，分别记做Data_19，Data_15。基于上述两种情况，建立了如式（1）所示的两个维纳预测方程，并以半年为一个周期，预测了两个监测指标未来30个周期内的状态。结果如图1所示。

图1 不均匀沉降和液面高度预测数据

其中，使用极大似然估计对两个方程参数进行估计，可以得到Data_19和Data_15情况下的退化系数分别为，扩散系数分别为ξ1=0.568 6,ξ2=1.732 7。

根据图1，随着运行周期的不断递增，未来30个周期内的石油储罐不均匀沉降均呈现整体递增趋势，液面高度呈现无规律性变化，以模拟储罐的充放液过程。

2.2 基于FEM-BRB-r模型的结构性能状态评估

借助ANSYS软件建立石油储罐的机理仿真模型，图2(a)中给出网格划分的储罐有限元模型。其中，罐壁结构采用16MnR材料，壁厚可变。石油储罐有限元模型的弹性模量设置为2.0×105MPa、泊松比0.3，液体密度870 kg/m3。

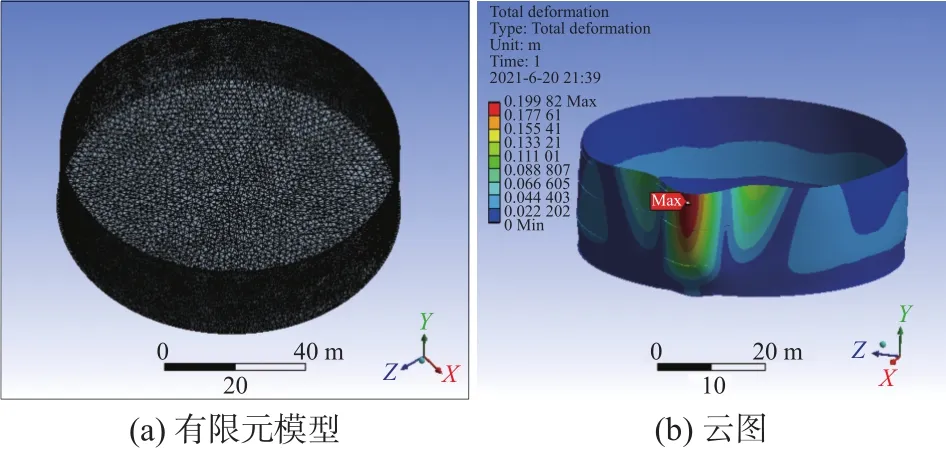
图2 石油储罐有限元模型和工况21下的结构变形云图

利用行业标准API 653—2009《储罐检验、维修、改造和重建》以及专家知识对2个输入指标参考值和参考等级进行设置，如表2和表3所示。

表2 不均匀沉降载荷的参考值mm

表3 液面高度载荷的参考值m

基于两个载荷指标参考值的数量，规则总数为L=7×3=21条。同时，可确定与置信规则库对应的21种工况F={f1,···,f21}，其中fk(k=1,···,21)表示第k种工况下载荷指标x1和载荷指标x2合力。

把不同工况下的fk(k=1,···,21)施加到机理仿真模型上，利用公式（2），可以得到最大结构变形量wk(k=1,···,21)以 及 归 一 化 后 的 最 大 变 形 量。图2(b)给出了工况21下的结构变形云图，图3给出了21种工况下的归一化变形量。

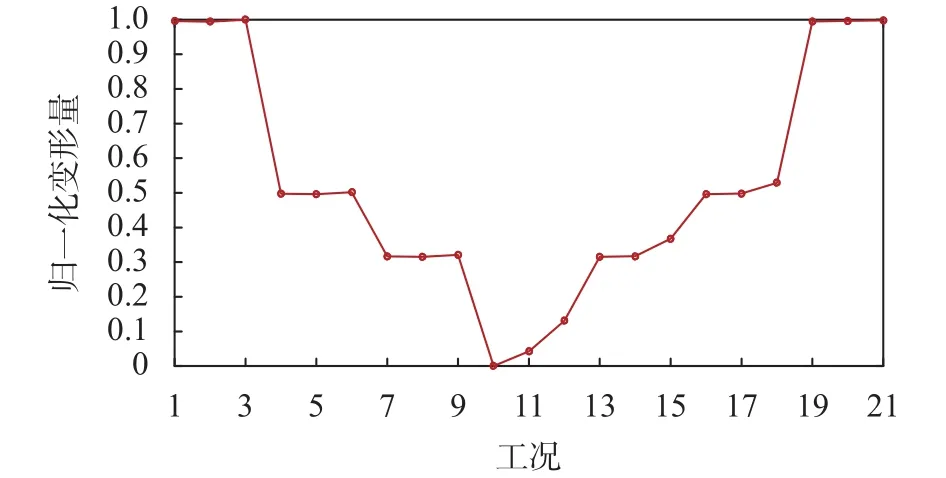
图3 21种工况对应的归一化变形量

如图3所示，在case 9-1和case 13-21下，在不固定液面高度的情况下，石油储罐的最大结构变形量随着不均匀沉降的增大而整体增大。根据case 1-3、case 4-6、case 7-9、case 13-15、case 16-18、case 19-21可知，当发生负方向的不均匀沉降时，随着液面高度增加，储罐的最大变形量基本保持不变；当发生正方向的不均匀沉降时，结构最大变形量随液面高度的增加而增大。究其原因，当储罐发生负方向的不均匀沉降时，储罐产生的一个水平方向的支反力抵消了贮液对罐壁内侧产生的水平向外的液体静压力，导致最大变形量随着液体静压力的增大而基本保持不变。

下面进行规则库的构建。首先，将规则权重θk(k=1,···,21)和 属 性 权 重 δi(i=1,···,2)设 置 为 1。其次，基于归一化的最大变形量以及表1中给出的参考值 μ (DSn)，利用公式（3）计算初始置信度 β ={βj,k;j=1,···,4,k=1,···,21}。然后，采用信息一致性的方法，计算得到载荷指标x1和载荷指标x2的属性可靠度分别为0.518 3和0.488 5。

基于上述所获得的模型参数，根据公式（6）确定置信规则库，如表4所示。最终完成FEM-BRB-r模型的构建。

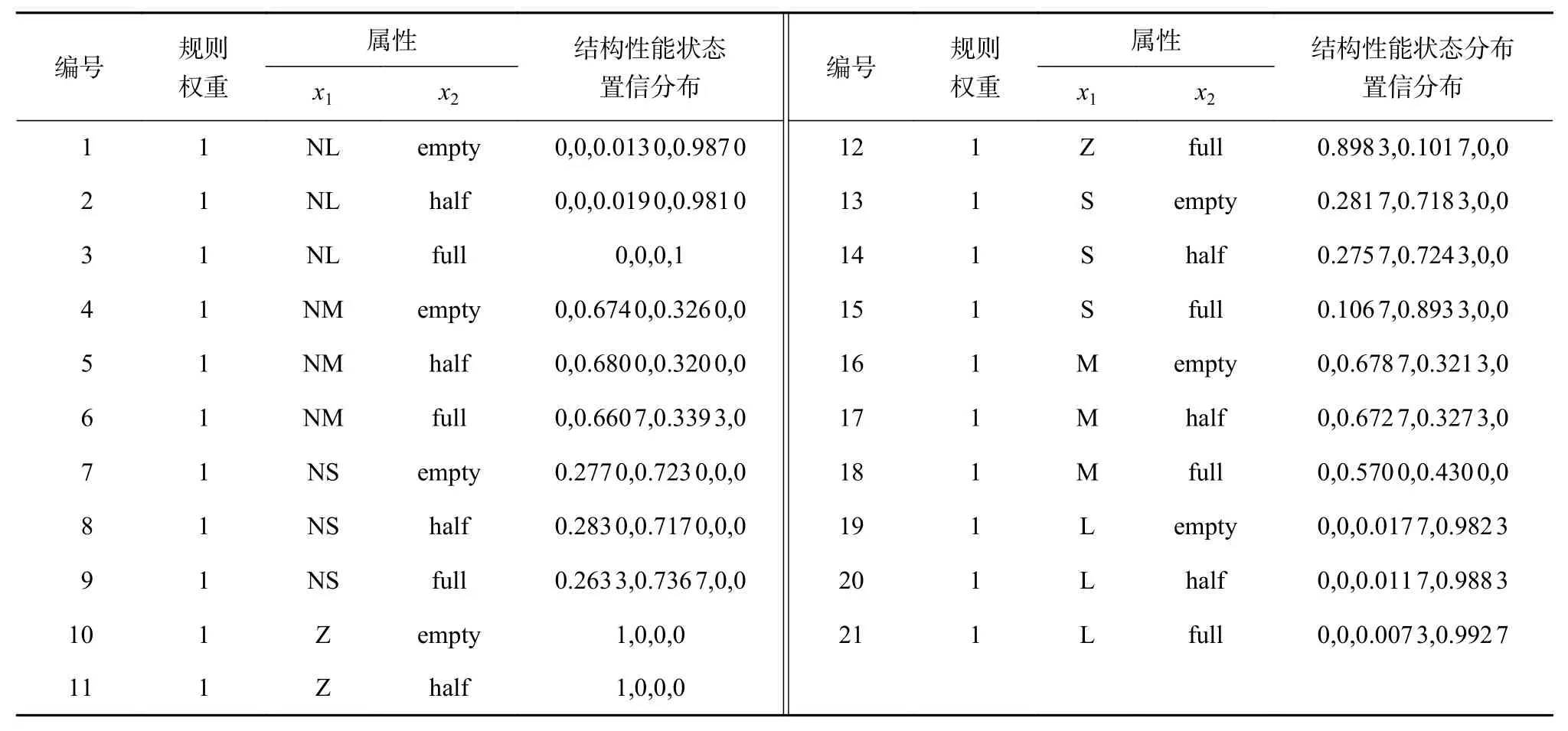
表4 初始置信规则库

最后，进行LLT的结构性能状态评估。利用公式（7）～（11），计算得到30个周期内的石油储罐结构性能状态，如图4所示。

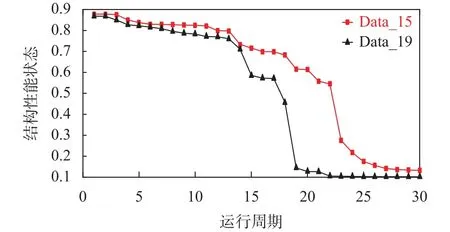
图4 融合的结构性能状态

根据图4可知，在初始阶段石油储罐系统的结构性能状态较好。随着运行周期的递增，石油储罐的结构性能在不断下降。这是因为在长时间贮存的条件下，系统受环境、贮液变化等因素的影响，石油储罐箱体会产生不同程度的变形，导致其结构性能状态有所下降，这表明基于FEM-BRB-r模型融合得到的石油储罐结构性能状态，是符合实际对设备退化轨迹的认知。

2.3 最优维护时机的确定

依据石油储罐的结构性能状态设置了4个不同的维护等级，且不同维护等级下对应着不同的维护措施以及维护成本，如表5所示。

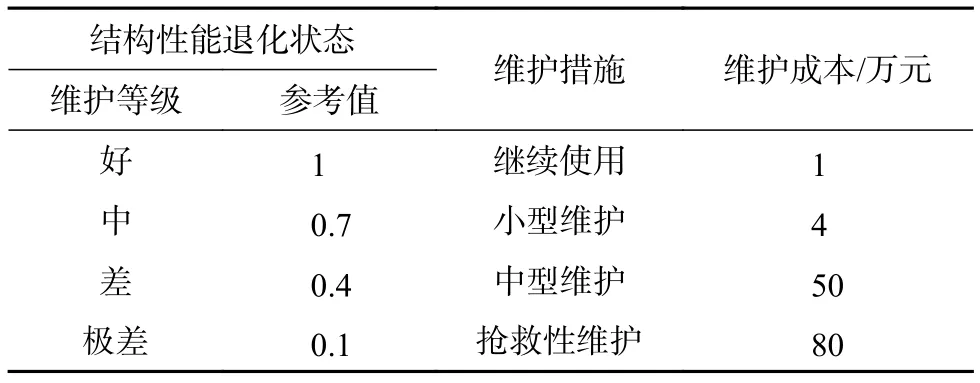
表5 石油储罐结构性能维护等级与维护成本

由公式（12）可知，石油储罐的平均维护费用由当前系统的结构性能状态与该状态下采取维护措施的概率以及对应的维护费用决定的。例如，假设Δt=1，则根据图4可知，在Data_19情况下对应的石油储罐的结构性能状态，则在该状态下各维护等级对应的维护概率可由公式（13）计算得到：p1=0.025 2,p2=0.967 0,p3=0.005 0,p4=0.002 8。

其对应的单位时间内的平均维护费用为4.364 9万元。按照此法，可以求得在Data_19和Data_15两种状况下，30个周期的石油储罐对应的单位时间内的平均维护费用如图5所示。

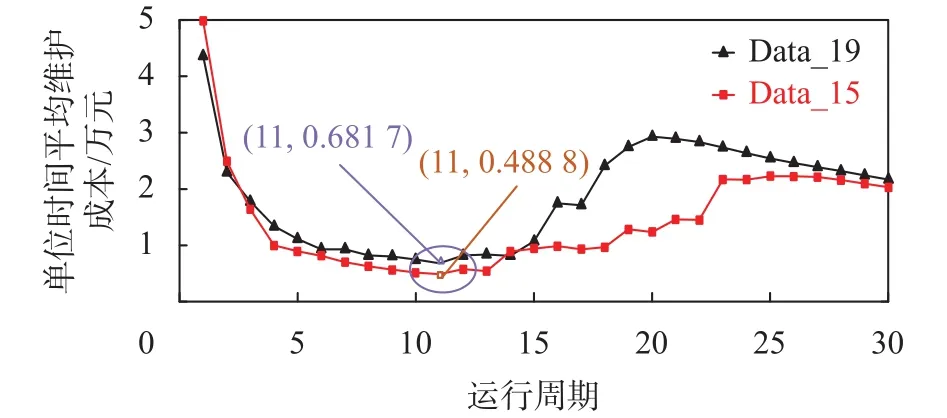
图5 结构性能退化与维护成本

从图5可以看出，随着运行周期的递增，在两种情况下的石油储罐的平均维修费用均呈现先下降后上升的趋势。其中，在Data_19的情况下，在第11个运行周期内对系统进行测试时，所需要花费的平均维护费用最低为0.681 7万元，此时对应的系统结构性能状态为0.791 9，系统处于中等状态，且并未超过最低结构性能状态阈值0.1。在Data_15的情况下，最低平均维护费用点（11，0.488 8）对应的依旧是第11个运行周期，且对应的系统结构性能状态为0.821 7。

造成这一现象的主要原因是，当维护间隔较短时，储罐结构性能处于较好状态，但系统平均维护成本较高。这表明若测试间隔较短，虽然可以保证系统结构性能状态处于良好，但会增加储罐设备的停机检测时间从而导致维护成本增大；当维护间隔较长时，系统结构性能下降明显，处于较差状态，但系统平均维护成本依旧保持较高状态。这表明若一味追求最低维护费用而增大维护间隔，虽然可以减少维护次数，但由于无法及时发现设备安全隐患，导致储罐发生故障需要采取中型或抢救型维护，维护成本被迫增大。

因此，在上次测试后的第11个周期内，对储罐可能发生的故障进行预防性维护，使得在保证储罐结构稳定性的前提下，也能降低维修费用。此外，图5所示的结构性能退化与维护成本关系图也说明了所提方法能够有效解决先验信息缺乏问题，在先验信息完整或先验信息缺失情况下均能根据既定策略确定系统的最佳测试时机。

3 结束语

本文从大型贮液箱的维护管理出发，提出了一种基于结构性能的大型贮液箱最优维护时机确定方法。首先，该方法在利用维纳过程预测未来时刻的监测指标状态的基础上，通过构建的FEM-BRB-r模型实现在先验信息不完全且监测数据受到干扰下对LLT结构性能的准确评估。其次，综合考虑LLT的结构稳定性与维护成本要求，以单位时间平均维护成本最小为目标，从而确定LLT的最优维护时机。所提方法能够在保证系统可用性的前提下减少系统维护成本，并根据最优维护时机及时地对系统进行预防性维护，一定程度上延长LLT的使用寿命。最后，通过对5万立方米的石油储罐开展实例研究，验证了该方法在贮液箱最优维护时机确定上的有效性，具有一定的工程参考价值。