Different roles of surfaces’interaction on lattice mismatched/matched surfaces in facilitating ice nucleation

Xuanhao Fu(傅宣豪) and Xin Zhou(周昕)

School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

Keywords: ice nucleation,molecular simulations,lattice match,hydrophilicity

1.Introduction

The freezing of supercooled water usually occurs on surfaces of foreign materials (impurities or substrates) through the heterogeneous ice nucleation.[1,2]One long-term pursued but still not completely achieved goal is to predict the ice nucleation ability directly from the microscopic character of surfaces.Lots of experimental works on well-characterize atomic surfaces,e.g.,graphene[3-7]and minerals[8-11]as well as molecular dynamics (MD) simulations on modeling surfaces with a series of controlled features have been employed to investigate the microscopic mechanism of ice nucleation on various material surfaces.Some plausible summaries about the nucleation effects of one (or a few) individual variable(s) of material surfaces in experience, such as the lattice templating,[12-17]the hydrophilicity-induced layering of interfacial water,[3,4,18]the hydroxyl hydrogen bonding,[19-22]as well as the nanometer carving[23-25]and micrometer stepping[10,26,27]were found to regulate the ice nucleation in some specific cases, but often with exception and deviation in others.For example, there is one common sense that an effective nucleating agent should provide a template for ice formation,thus the silver iodine(AgI),whose lattice constant is only 1.5% different from that of the ice Ih, is most effective in promoting the occurrence of ice nucleation for wide application in artificial rainfall.[28-30]However, the lattice template effect was found to be invalid in other materials,such as BaF2and CuBr,[31,32]although they also have the similar lattice to ice but are almost not effective to facilitate ice nucleation.Recent studies by Luet al.[33]and Shaoet al.[20]have shown that the dipole orientation of interfacial water has a vital effect in ice nucleation, which may be responsible for the occasional failure of lattice template effect.The absorption strength of surfaces to water molecules,i.e.,the hydrophilicity of surfaces, was also thought to be a key role in affecting the heterogeneous ice nucleation.For example,Pedevillaet al.[34]studied the freezing of water on the OH-patterned surfaces,and they found that the ice nucleation was less dependent on the detailed atomic arrangement of the hydrophilic surfaces,but dependent on the density of the OH groups, i.e., the average hydrophilicity of the surfaces.However, while the hydrophilicity of surfaces is non-uniform on the nanoscale,Lupiet al.[3]and Coxet al.[35]found that the average hydrophilicity of the whole surfaces did not well describe the ability of the surfaces in facilitating ice nucleation.Fitzneret al.[36]and Biet al.[37]found that the lattice structure of substrates can complicatedly couple with the hydrophilicity to regulate the water freezing on the substrates.Recently, Zhanget al.[25]verified that the sizes of hydrophobic and hydrophilic domains of the non-uniform surfaces dominate ice nucleation.So far,the central question about the mechanism of heterogeneous ice nucleation,what is the relationship between features of material surfaces and their ice nucleation ability,remains open.It hinders the wider applications in such as finding/designing anti-icing material surfaces for controlling ice formation.

In this paper,we investigate the ice nucleation on a series of substrate surfaces with different atomic arrangements, lattice parameters,hydrophilicity,and interaction function forms to water molecules, via MD simulations.We find, for the flat atomic surfaces whose lattice does not match that of ice,the detailed arrangement of the surface atoms has little effect on ice nucleation,the average interaction of surfaces to water molecules alone determines the nucleation ability of these surfaces.In contrast,for the surfaces whose lattices match that of ice,even different function form of the surfaces’interaction to water molecules could significantly change the ice nucleation capability of the lattice-matched surfaces.

2.Method

We simulate the ice nucleation of the single-site mW water model[38]on a series of flat atomic surfaces with various lattices and the interactions to water molecules.The simulated box is shown in Fig.1(a), and the water slab is placed on a substrate with horizontal dimensions of approximately 5 nm×5 nm(slightly adjusted to be appropriate to the perfect periodicity of the applied substrate surfaces).The thickness of the water slab is about 5 nm containing 4096 water molecules and a vacuum layer of 2 nm is left above it.The periodic boundary condition is employed in all three directions.

Two different interaction function forms between each atom of substrates and each mW water molecule are used to describe the substrate-water interaction, one is the two-body part of the Stillinger-Weber(SW)potential,which was widely used in previous studies[3,4,37,39]

and the other is the Lennard-Jones(LJ)potential

Hereris the distance between the surface’s atom and water molecule.A=7.05,B=0.60,a=1.8.The parameterσ=0.32 nm is chosen as that of carbon atoms of graphene with water molecules, and we varyεfrom 1ε0to 6ε0, whereε0=0.13 kcal/mol is that of carbon atoms of graphene with water molecules.As shown in Fig.1(b),the SW potential and LJ potential with the given parameters(ε=1ε0)have the same depth of the potential well but differ in the repulsion part.

Fig.1.MD simulation system settings.(a)Typical simulation box consisting of water molecules(red)and substrate(gray).(b)Two different potential energy functions describing substrate-water interactions.(c)Three kinds of atomic arrangements in the employed substrates.

We consider three different lattice structures to arrange the atoms of substrates, named as, hexagon, triangle, and square,see Fig.1(c),to mimic that of some real material surfaces.For example, the atoms on graphene and silver iodide are arranged in the hexagonal lattice; the hydroxyl groups on kaolinite, the atoms on the(111)and(100)faces of the facecenter-cubic(fcc)metal are arranged in the triangle, triangle,and square lattice,respectively.For each piece of the arrangement, we vary the nearest neighboring atom distanceabetween 0.7a0and 1.3a0, wherea0=0.142 nm is the nearest neighboring atomic spacing of graphene.

As a comparison, a series of structureless surfaces(smooth geometry walls without explicit atoms) with various interaction strengths to water are also considered, where the interaction function between the surfaces and water is the integrated Lennard-Jones potential.[40]with the distancezof atoms from the surfaces,

Ice nucleation is studied by MD simulations in the NVT ensemble,and the temperature decreases gradually by 1 K after passing each one nanosecond, from 280 K to 180 K, and then each simulation is run for 100 ns.During each 1 ns simulation segment, the temperature is controlled by the Nos´e-Hoover thermostat with a relaxation time of 0.5 ps.The velocity Verlet algorithm with a time step of 5 fs is applied to integrate the equation of motion of water molecules.The atoms of surfaces are fixed during simulations.We employ the CHILL+ algorithm to identify ice molecules.[41]The largest ice clusters are determined by clustering the ice molecules using a cut-off distance of 3.5 °A.The freezing temperature is defined as that the number of ice molecules(inside the largest ice cluster) starting to significantly increase during the cooling simulations.Since nucleation is a random event, we perform five independent simulations for each case to estimate the average nucleation temperature,Tn,and its statistical error.All MD simulations are performed by the LAMMPS program package.[42]

3.Results and discussion

The obtained average nucleation temperatures on different substrates(atomic arrangements,lattice constants,and interaction strengths)with the SW potential and the LJ potential interacting to water molecules are shown in Figs.2(a)and 2(b),respectively.We find, albeit existing small deviation, the average nucleation temperatureTncan be thought as a universal function of the parameterλfor most of our employed substrate surfaces.As shown in Fig.2(a), with increasing the average absorption strength of all SW surfaces to water moleculesλ,theTnfirst increases to reach the maximum value about 225 K atλ ≈1.5, then decreases and approaches to the range between 205 K and 210 K whileλ＆gt;5, as a comparison, the homogeneous nucleation temperature of the mW water model is about 202 K.

Fig.2.Variation of the ice nucleation temperature on the substrate with λ for the(a)SW potential and(b)LJ potential.Different colors are used to indicate the different atomic arrangements(red: hexagon,blue: square,green: triangle)and different types of symbols are used to distinguish various distances between nearest neighboring atoms(a=0.7-1.3,in units of a0=0.142 nm)in both(a)and(b).Thus,the red diamonds(with dashed line)in(b)are the results on the surfaces with the LJ potential, hexagonal lattice, and a=1.1(i.e., the lattice matches that of ice).The results on the surfaces with SW potential and the same lattice parameters are also shown in(a)but not easily distinguished from the others.The cyan area shows the occurred temperature of homogeneous ice nucleation,the magenta and yellow areas show the ranges of the ice nucleation on surfaces with the SW and LJ potentials, respectively.To make the results more readable, the data points of SW are shaded in(b)and only the magenta area is kept.

For the surfaces with the LJ potential,the results are similar, except the surfaces with the hexagonal lattice and the nearest neighboring atomic distancea=1.1 (in units ofa0),as shown by the red diamonds connected with dashed line in Fig.2(b).In the figure, the range of the ice nucleation temperature on the SW surfaces, (the magenta region, same as that shown in Fig.2(a)),is also plotted as a comparison.The nucleation temperature on most LJ surfaces is similar(or more exactly,slightly lower)to that of the SW with varyingλ.However,for the LJ surfaces with the hexagonal lattice anda=1.1,the average nucleation temperatureTnvery largely deviates from the results of the other surfaces,which quickly increases to about 245 K from the universal curve of the other surfaces whileλincreases from 0.5 to 1.27 and thenTnremains unchanged when 1.27＆lt;λ＆lt;2.54 after that, then it quickly decreases to coincide with the universal curve whenλslightly increases from 2.54 to about 3.37, see the red dashed line in Fig.2(b).Note that the results on the surfaces with the same lattice and constant but SW potential have been already presented in Fig.2(a), without showing any deviation from that of the other surfaces.

The above results indicate thatλgenerally characterizes the effects of surfaces’ interaction on the ice nucleation for most of these substrate surfaces.Sinceλportrays the average interaction strength of these surfaces to water molecules,it implies that the details of atomic arrangement on surfaces do not obviously affect the ice nucleation at least for most of our studied surfaces.We calculate the adsorption energy of various substrate surfaces to an individual water molecule,as functions of the interaction parameterεand the parameterλ.While the adsorption energy increases linearly withεbut with different slopes corresponding to different surface structures,as shown in Fig.3(a); the linear relation between the adsorption energy andλis universal for all surfaces with the same slopek=2.35 kcal/mol,as shown in Fig.3(b).This suggests that the adsorption energy of surface to an individual water molecule characterizes the ice nucleation capability of most surfaces.

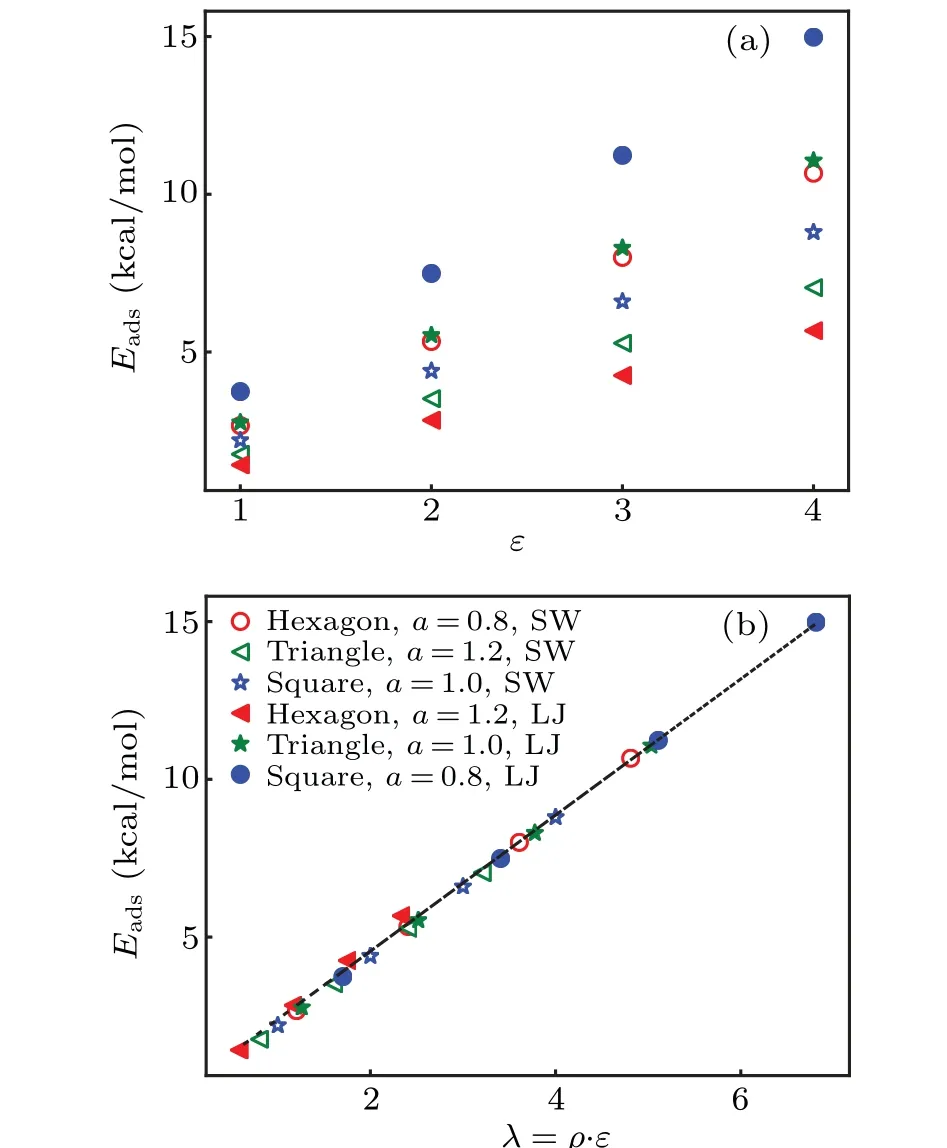
Fig.3.The adsorption energy of a single water molecule on a few kinds of different surfaces versus(a)the interaction strength parameter ε and(b) the parameter λ.The details of each surface are described in the legend in the order of atomic arrangement, nearest neighboring atom distance,and the interaction function form.

We further performed MD simulations for the structureless wall and compared the results with those at SW potential and LJ potential.For atomic surfaces, the horizontal coordinateλis converted to the adsorption energyEadsby the correspondenceEads=2.35λ.For structureless walls, the adsorption energy is calculated by 6/5πε(see Eq.(3)).As shown in Fig.4,the ice nucleation temperature on the structureless wall is very similar to that on the atomic surfaces with the LJ potential and slightly different from that on the atomic surfaces with the SW potential.This is because the structureless wall interaction, as Eq.(3), is indeed integrated from the atomic surfaces with the LJ interaction,which further verifies that the detailed atomic structure on the substrates plays fewer roles in affecting the heterogeneous ice nucleation.

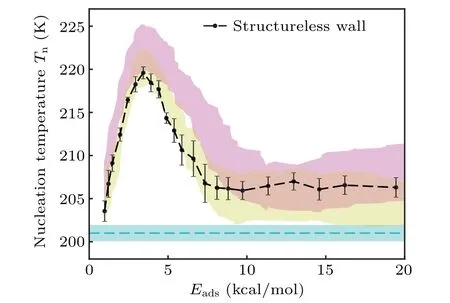
Fig.4.The ice nucleation temperature on the structureless wall versus Eads (the adsorption energy of the wall to water molecules).The results on atomic surfaces with LJ potential and SW potential to water molecules, the same as shown in Fig.2, are plotted as the yellow and magenta regions,respectively,for comparison.

Since the surfaces with the hexagonal atomic arrangement anda=1.1 have the same lattice structure of ice, the found high ice nucleation temperature on the surfaces with Lennard-Jones potential and the absorption strength parameter 1.27＆lt;λ＆lt; 2.54 can be explained as the known icetemplate effect.Anyway,it is interesting that the surfaces with the same ice-matched lattice but interacted to water molecules by the SW potential do not show the ice-template effect.In Figs.5(a)and 5(d),we show the density profiles of water(before freezing)and ice (after freezing), as well as the in-plane average of the adsorption energyEads(r) of a water molecule atrfrom the surface with the LJ and SW potentials (with the parametera= 1.1,ε= 2, corresponding toλ= 1.27),respectively, ¯Eads(z) =∫dxdyEads(r).On the two kinds of surfaces, the positions of the adsorption wells locate atz0=0.32 nm (LJ) andz0=0.28 nm (SW), corresponding to that of the first layer of interfacial water, respectively.Thus,we plot the in-plane distribution of the adsorption energy of a single water moleculeEads(x,y,z0) on the two surfaces in Figs.5(b)and 5(e),respectively.The absorption energy wells on the LJ surfaces locate atop the center of the hexagonal-atom ring,then form a perfect ice-matched lattice,and thus promote the ice nucleation at higher temperatures as an ice template,seeing Fig.5(b).The well depth is about 0.27 kcal/mol, as shown in Fig.5(c).It is helpful for the formation of the interfacial ice-like layers then facilitates the ice nucleation of the remained water atop.However,on the surfaces with SW potential,as shown in Fig.5(f),the ice-matched lattice corresponds to the peaks of interaction energy,the positions of absorption wells do not match that of the ice lattice,and the well depth of the adsorption energy is only 0.09 kcal/mol as shown in Fig.5(e), so that the lattice-matched surfaces do not have the ice-template effect.Note,for too smallλ,e.g.,λ＆lt;1.27,even on the LJ surface,the well depth of the adsorption energy is too weak to form the ice templates for aiding efficiently the ice nucleation; while at medium strength 1.27＆lt;λ＆lt; 2.54,templates are susceptible to formation, nucleation occurs relatively more easily on the templates, and the nucleation temperature is higher; and for largeλ, e.g.,λ＆gt;2.54, the surfaces’interaction is very strong,thus absorbs too many water molecules in the interfacial layer.Thus, the ice-template effect on the lattice-matched LJ surfaces is also depressed.

Fig.5.The average adsorption energy ¯Eads(z),and the density distribution of water(red)and ice(blue)at distance z from the lattice-matched surface with(a)LJ potential and(d)SW potential.The surfaces’parameters a=1.1,ε=2,corresponding to λ =1.27.The in-plane adsorption energy distribution of an individual water molecule on the two surfaces at the distance z0 =0.32 nm and 0.28 nm are shown in (b) and (e),corresponding to the maximal of the interfacial water density on the LJ and SW surfaces,respectively.The atoms of substrates are represented by brown sticks and the interfacial water molecules(after freezing)are shown as cyan spheres and sticks.The detailed potential energy surfaces on the two surfaces are shown in(c)and(f)within a unit cell of substrates,respectively.

Fig.6.Microscopic details of two different freezing processes.The surfaces’parameters a=1.1,ε =2,corresponding to λ =1.27.Variation of the average potential energy per water molecule(blue)and the number of ice molecules(red)during the ramp cooling simulations,on the lattice-matched surfaces(a)with LJ potential and(b)with SW potential.Some snapshots during the simulation are shown on the right with the corresponding capital letters,where A is the initial state of the system,E and C are the snapshots of ice nucleation occurring on the substrate surface and ice template surface,respectively.Here liquid waters are in cyan,ice in red,and the interfacial ice-like layers in blue.

Therefore, there are two different ice nucleation mechanisms on various surfaces.Figure 6 gives the average potential energy of surfaces to each water molecule and the number of ice molecules(in the largest ice cluster)as the function of the temperature (thus the time) during the cooling simulations.As shown in Fig.6(a), on the LJ-surface with icematched lattice (λ= 1.27), the freezing of system has two separate steps.It first forms a double-layer honeycomb icelike structure,then induces the ice nucleation of remained water on it.It is typical on the strong ice-template surfaces,and the freezing of water follows the process A→B→C→D,which occurrs at higher temperatures.As a comparison, the freezing of water on the other surfaces, involving the latticemismatched surfaces and on the lattice-matched surfaces but with SW potential, passes through the single-step nucleation process, A→E→F, as shown in Fig.6(b).These two different freezing processes occur on substrates with the same ice-matched lattice but different interaction potentials to water molecules.On the surfaces with LJ potential,the surfaces’interaction provides sufficient energy well at the ice lattice to induce the formation of interfacial ice-like layers;whereas on the surfaces with SW potential,it is the peaks of the potential energy surfaces and the well depth of the interaction to water molecules is too small so that it cannot induce the formation of interfacial ice.Therefore,the ice-template effect of substrates requires not only the ice-matched lattice but also suitable interactions to induce interfacial water molecules to form ice-like layers.

4.Conclusion

In summary, we systematically investigate how the lattice structure,and the detailed interactions of substrates affect the freezing of water.We found,for surfaces without the icematched lattice, their nucleation efficacy is dominated by the absorption strength of the surfaces to water molecules;but for the surfaces with the ice-matched lattice,the sufficient potential wells at the ice-like lattice positions in the interfacial layer of water are required to induce the formation of ice templates on the surfaces to facilitate the further nucleation of the remained water atop.It provides a detailed insight for understanding the relationship between a variety of features of surfaces and their capability in promoting the ice nucleation.

Acknowledgement

Project supported by the National Natural Science Foundation of China(Grant No.12174388).