Gyrokinetic simulation of low-n Alfv´enic modes in tokamak HL-2A plasmas

Wen-Hao Lin(林文浩) Ji-Quan Li(李继全) J Garcia and S Mazzi

1Southwestern Institute of Physics,Chengdu 610041,China

2CEA,IRFM,13108,Saint-Paul-lez-Durance,France

3EPFL,Swiss Plasma Center,Lausanne,Switzerland

Keywords: low-n Alfv´enic modes,fast ions,gyrokinetic simulation,tokamak

1.Introduction

Recently, various fast-ion-related experimental observations[1,2]in the Joint European Torus (JET) and related numerical studies[3-7]have highlighted the beneficial role of fast ions in reducing turbulent transport and improving confinement.There are many promising linear explanations for the beneficial impact of fast ions on overall plasma confinement,such as resonance interaction between fast ions and bulk plasma turbulence,[7]but these mechanisms are still incapable of explaining the substantial reduction in the ion profile‘stiffness’ parameter,[3]a quantity defined as the ratio of ion heat flux to the logarithmic ion temperature gradient and indicating the level of transport driven by plasma turbulence.Another competitive mechanism proposed for such transport reduction has been studied numerically with the GENE code,[8]highlighting the nonlinear interplay between marginally stable fast-ion-induced Alfv´enic activities and bulk plasma microturbulence, for example the ion temperature gradient (ITG)mode.The role of linearly marginally unstable low-nmodes,identified as the toroidicity-induced Alfv´en eigenmode(TAE)in JET plasmas,was emphasized.

Further experiments have shown that strong reduction of turbulent ion heat transport, reaching conditions for transport suppression, occurs with a TAE that is fully destabilized by MeV ions, as expected in ITER with alpha particles but generated by ion cyclotron resonant heating(ICRH)in the case of JET.[9-11]A strong interplay between TAE modes and zonal flows, highly dependent on electromagnetic effects, is found in non-linear gyrokinetic simulations in these conditions.[11]In turn, zonal flows reduce turbulent transport driven by the ITG,leading to improved thermal confinement.

The fact that ion heat transport may be suppressed by the interplay between high-frequency low-nmodes destabilized by fast ions and ITG turbulence,opens up the possibility that such a mechanism has played a role in experiments in which internal transport barriers (ITBs) are formed in the presence of a strong fast-ion-generated population.This could be the case for recent discharges of the HL-2A tokamak with highpower neutral beam injection(NBI),[12]in which the plasmas are characterized by a low electron density and a significantly larger portion of fast ions compared with JET plasma.In particular, ITB in the ion temperature profile is formed with weakly reversed magnetic shear in the core plasma.However,the possibility that fast ion effects play a role as an underlying physical mechanism for ITB triggering has never been clarified.To gain a better understanding of the impact of fast ions on HL-2A plasmas with ITB, linear gyrokinetic simulations based on a local version of the GENE code[8]are carried out in this work.Emphasis is given to mode characterization and GENE validation in such plasmas when fast ions are included in/excluded from the simulations.This is an important step,as plasmas analyzed in JET are not of the same nature as in HL-2A.Notably,the magnetic shear is higher and the ion temperature gradient lower for JET than for HL-2A,which might lead to significant differences in terms of turbulence characteristics.

The remainder of this paper is organized as follows.In Section 2,the physical model used in the GENE code is briefly described and the simulation setup and input parameters from HL-2A discharge #22453 are arranged.Section 3 is devoted to the linear GENE simulation and stability analysis in HL-2A plasmas with or without fast ions.Simulation results are comprehensively compared with the numerical solutions of the general fish-bone-like dispersion relation(GFLDR)derived by Zoncaet al.[13]Finally,the main results in this work are summarized in Section 4.

2.Physical model in the GENE code and numerical setup

Numerical simulations in this work are performed using a local version of the GENE code,which works in field-aligned coordinates with(x,y,z)corresponding to the radial,binormal and parallel directions, respectively.In GENE’s linear local version, the normalized gyrokinetic Vlasov equation for the perturbed distribution functionf1jof speciesjreads[22,23]

Here equilibrium quantities and perturbed quantities are denoted with the subscripts‘0’and‘1’,respectively.A bar above quantities represents gyro-average operation.The modified distribution function

is defined to unite the time derivatives off1jandA1‖in one quantity(which facilitates time discretization),while the modified potential

contains the gyro-averaged potentialφ1, parallel vector potentialA1‖and parallel magnetic fluctuationB1‖.The nonadiabatic part off1jis defined as

The normalized logarithmic gradient of a quantity(e.g.,Tethe electron temperature)is defined as

with the reference lengthLrefbeing the minor radiusain this work.For the sake of completeness, the parallel magnetic fluctuationB1‖is preserved and the linearized Landau-Boltzmann collision model[14]is employed for the collisional term〈Cj(f)〉in Eq.(1), but their effects are actually negligible for the presentation of the simulation results, as will be justified in Subsection 3.2 where we reproduce simulation results with acceptable error neglecting the effects ofB1‖and collision.The definitions of other quantities and the rules for normalization can be found in Refs.[22,23].Unless otherwise specified,EFIT equilibrium is employed and all the species are treated as fully kinetic.For simplicity,the equilibrium velocity distributionf0of all species(including fast ions)is chosen to be Maxwellian.

Fig.1.Profiles of plasma density(a),temperature(b)and safety factor and magnetic shear(c)in HL-2A discharge#22453.

The profiles shown in Fig.1 roughly describe the plasma state at time slice 650 ms in ITB discharge shot#22453.The black dashed lines indicate where the flux-tube simulation domain locates radially.These profiles were reconstructed using the kinetic-EFIT equilibrium code.The thermal and fast ions are both chosen to be hydrogen and are denoted with subscripts ‘i’ and ‘fi’, respectively.Note that the fast ion profiles have been multiplied by some number for readability.The shape of the electron density profile is assumed to be the same as that of the similar discharge #25733.[12]The electron and thermal ion temperature profiles are measured through electron cyclotron emission[15]and charge exchange recombination[16]diagnosis systems, respectively.Fast ion profiles are output from NUBEAM[17]calculation.The simulation box is chosen to be located at the ITB regionx0=0.25a.Corrugation of the profiles can be found nearρtor=0 and 1.0,which is caused by both the uncertainty of measurement and the error of interpolation.However, this problem is not severe at the simulation flux-tube domainρtor=0.25.The grid resolutions in the radial, parallel, parallel velocity and magnetic moment dimension are(nx,nz,nv‖,nw)=(48,32,32,16).Thirty-two binormal wave numberskys are used,with each of them corresponding to toroidal numbernfrom 1 to 32 under the relationky=nq0/x0.The safety factorq0=1.26 and magnetic shear ˆs=0.12 are calculated from the kinetic EFIT equilibrium reconstruction atρtor=0.25.Note that theqprofile is set as a proportional function of the magnetic shear in the local version of GENE, so theqprofile used in local simulations is expressed asq=q0[1+ˆs(x-x0)/x0],wherex=aρtoris the radial coordinate andx0is the radial location of the flux-tube.ˆs-αgeometry[18]is also employed in this work to facilitate comparisons with the analytical formula introduced below.The radial extension of the simulation box for each toroidal numbernislx=1/(kyˆs)≈260ρi/n.Other dimensionless parameters used in the simulations with and without fast ions can be found in Table 1.In the following, linear local GENE simulations will be performed for the case with and without fast ions, denoted by ‘WFI’ and ‘NFI’, respectively.Also,the GFLDR will be solved for the NFI case in Table 1.

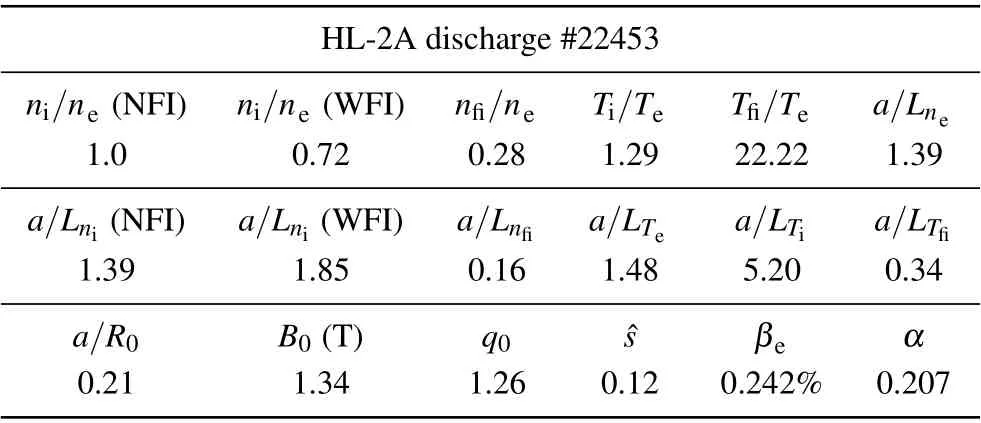
Table 1.Input local parameters for GENE simulations.The nomenclature is conventional.The electron density ne, temperature Te and minor radius a are used as reference quantities(ne =1.271×1019 m-3,Te =0.853 keV and a=0.358 m).The cases with fast ions and no fast ions are denoted by WFI and NFI,respectively.

3.Stability analysis in HL-2A plasma

GENE simulations of linear instability were carried for a NBI-heated HL-2A plasma with an ion ITB.The normalization rules follow the GENE convention with sound frequencyωref≈2π·127 kHz and gyro-radiusρref≈a/160,calculated from the sound velocity.Note that eachkypoint in this case corresponds to the toroidal numbernfrom 1 to 32.Results of linear simulations with fast ions excluded and included are shown in Fig.2.For convenience of illustration, the diamagnetic frequencyω∗pi=ω∗ni+ω∗Ti=kyTi(a/Lni+a/LTi)/(eB0a)and the kinetic thermal ion(KTI)gap frequency[19]ωKTI=ωtiq0(7/4+Te/Ti)1/2(whereωti=(2Ti/mi)1/2/(q0R0)is the ion transit frequency)are also plotted in Fig.2(b).

Fig.2.The growth rate(a)and frequency(b)for HL-2A cases with fast ions(WFI)and no fast ions(NFI).

3.1.The case without fast ions

It can be seen that for the range 0.2＆lt;ky＆lt;1, the spectrum is dominated by modes with frequencies in the ion diamagnetic drift direction.We claim that these modes are ITG modes since their frequencies and growth rates can be reproduced by the ITG dispersion relation shown in next subsection.The most noteworthy point here is that a high-frequency mode appears in the low-nrange,which also propagates along the direction of ion diamagnetic drift.Since these low-nhighfrequency modes are fully excited without fast ions(shown by the blue curve in Fig.2), these low-nmodes may also exist in the absence of NBI heating.As seen in Fig.2(b),frequencies of these modes are far below the TAE frequency(according to Eq.(30) in Ref.[19],ωTAE=2.42ωreffor our case)and comparable to both the diamagnetic frequencyω∗piand the transit frequencyωti, which may imply a strong coupling of the kinetic ballooning mode (KBM) and the beta-induced Alfv´en eigenmode(BAE).[13]Their mode structures of potentialφin ballooning coordinateχ,as shown in Fig.3(a)(taking then=4 mode as an example), display a two-scale dependence.One small-scale fluctuation varies onχ～O(1)while the whole potential varies on a large scale.Meanwhile,these low-nmodes are uniformly located in the poloidal direction without visible ballooning structure,as displayed in Fig.3(b).Besides, the effective magnetic potentialψis also shown in Fig.3(a), which is calculated from GENE’s direct output of the parallel vector potentialA‖and the JacobianJof the fieldaligned coordinate using the relation

It can be seen that this effective potentialψmatches well with the potentialφ, which indicates that the parallel electric field fluctuation

is nearly zero,characterizing the ideal magnetohydrodynamic(MHD)limit and a fully electromagnetic mode.

Fig.3.(a)Electrostatic potential φ and effective magnetic potential ψ in ballooning representation and (b) the real part of potential φ in poloidal cross section.

To further elaborate the linear stability features of the low-nmodes above and investigate their parametric dependence, the ratio of plasma pressure and magnetic pressureβ,the magnetic shear ˆsand logarithmic ion temperature gradienta/LTiare scanned.As shown in Figs.4(a1) and 4(a2), these low-nmodes are destabilized at lowβcombined with low ˆs.This may characterize the condition under which the low-n‘infernal modes’ emerge, as pointed out in Ref.[20].However,the phenomenon of frequency oscillations with increasingnis not observed here,implying that these low-nmodes should not share the same properties of the infernal modes described in Ref.[20].Besides, as seen in Fig.4(c), finite ion temperature gradienta/LTiis required to destabilize these low-nmodes.The critical stability thresholdsa/LTiof these modes are roughly proportional to 1/n.Note that the actual criticala/LTiof then=4 mode is obscure here because then=4 mode should disappear near the threshold.However,then=4 mode is unstable with a finite growth rate,indicating that this component is also characterized by the ITG mode.

Inspired by the linear properties of these low-nmodes and considering that their frequencies are located in the range ofω～ω∗pi～ωKTI, the GENE simulations are compared with the solutions of the GFLDR from Ref.[19].Including both ion compressibility and the ion diamagnetic drift effect on the left-hand side of the GFLDR while neglecting the kinetic contribution of fast ions on the right-hand side, the GFLDR is written as follows:[13]

In Eq.(11),all the frequencies are the same as defined above andF,G,N,Dare transcendental functions whose definition can be found in Ref.[13].Equation(10)is a unified dispersion relation describing two separate branches of the low-frequency surface acoustic wave (SAW) spectrum, i.e., the KBM and BAE branches,coupled with each other whena/LTi/=0.After a straightforward input of the frequency in the left-hand side, Eq.(10) is solved near the accumulation point so thatδWf→0, since the low-nmodes have ideal MHD properties, as mentioned above.Meanwhile, sinceq0=1.26 here the parallel wave numberk‖qR=nq-mis typically finite.This means that there is no unstable continuous spectrum near the accumulation point in HL-2A plasma and therefore thatδWfcould be arbitrarily assumed to be a small and negative value.This assumption is valid since nearδWf→0 the solutions of the GFLDR are unsusceptible to the change ofδWf,as is explained in Ref.[13] and shown in Fig.4.The solutions of the GFLDR assumingδWf=-0.01 and the results of GENE simulations using EFIT equilibrium and ˆs-αgeometry are plotted in Fig.5.Note that there are multiple solutions for the transcendental equation(10),so the solutions near(ωref/2,ωref/2)in the complex plane with a maximal growth rate are chosen to obtain the GFLDR spectrum.Comparison indicates that the GFLDR formula can qualitatively capture the spectral features of the low-nmodes.Furthermore, the GFLDR result is much better in agreement with the GENE simulation based on the ˆs-αgeometric model.This observation is reasonable since the GFLDR is also derived using the ˆs-αgeometry.

To further confirm the affinity between GFLDR solutions and the GENE simulation results,the simulations in Fig.4(c)were performed again using ˆs-αgeometry; the results are shown in Fig.6.The criticala/LTiin GENE simulations is compared with the analytical prediction of the stability threshold of the BAE branch(i.e.,Eq.(32)in Ref.[13]),

This critical value is shown in Fig.6(b) by a vertical dashed line of the same color as the corresponding mode number.As can be seen,for modes fromn=2 ton=4,the predicted criticala/LTivalues match very well with the GENE results.Their frequencies merge into the KTI gap frequencyωKTI,which is the accumulation frequency of the BAE branch as pointed out in Ref.[13].However, an extran=1 mode emerges before the growth rate of then=1 mode drops to zero with decreasinga/LTi.To get a closer look at this, the KBM and BAE branches plus the continua solutions of the GFLDR forn=1 are shown in Fig.7(a).It can be seen that the KBM branch is stabilized with increasinga/LTiand the BAE branch becomes unstable whena/LTisurpasses a certain threshold.Note that nearδWf→0,the solutions to Eq.(10)pile up near the accumulation point, which justifies the assumption above that the value ofδWfis arbitrary.Indeed, by solving Eq.(10) fixingδWf=-0.01 and varyinga/LTi,it can be seen in Fig.7(b)that results of GENE simulations match very well with solutions of the GFLDR in both small and largea/LTiregions.Although there are some small differences in the values of growth rates and frequencies, it is believed that these differences are acceptable because deviations of the same order can be found when we merely change the geometry,as can be seen by comparing the blue solid lines and dashed lines in Figs.7(b1)and 7(b2).Based on the above comparison with all these similarities in both mode structure and parameters dependences, we conclude that the low-nmode found in GENE simulations in HL-2A plasma is the BAE branch of the SAW spectrum described by the GFLDR(Eq.(10)).

Fig.4.The growth rate(upper panel)and corresponding frequency(lower panel)of linear GENE simulations for parametric scans of βe (effectively the total β), ˆs and a/LTi,respectively.The black dashed lines indicate the nominal values.

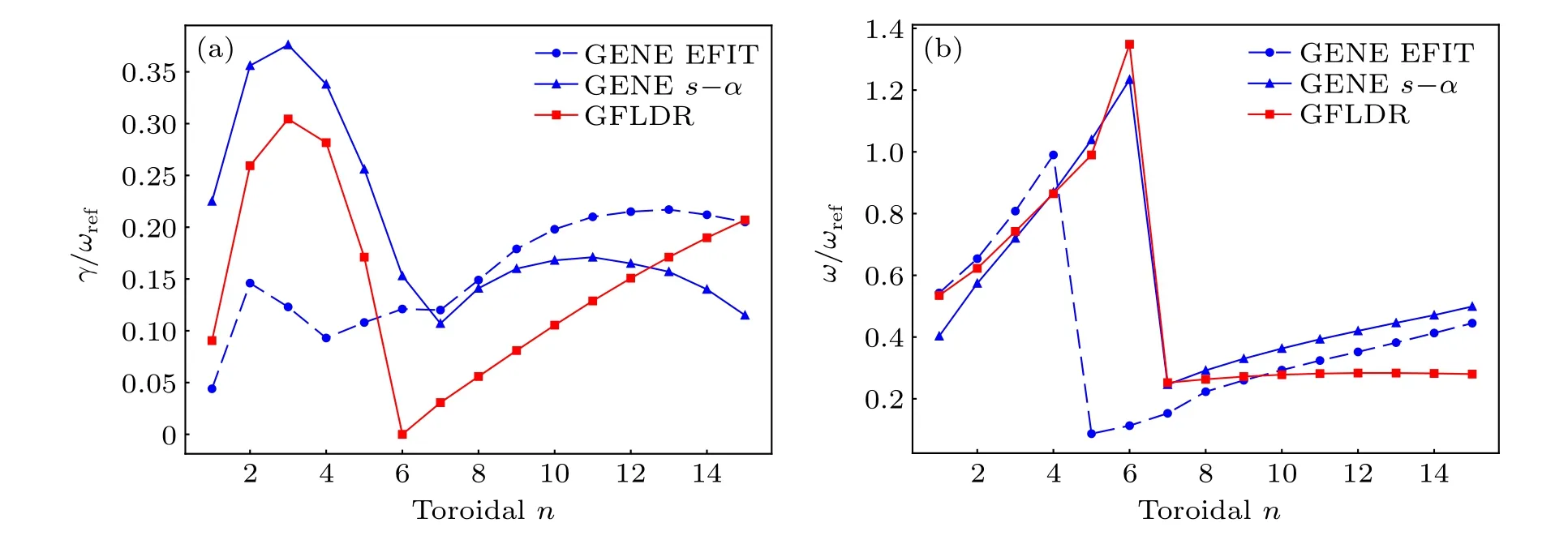
Fig.5.The results of NFI GENE simulations using EFIT equilibrium and ˆs-α geometry and GFLDR solutions: (a)growth rates and(b)frequencies.

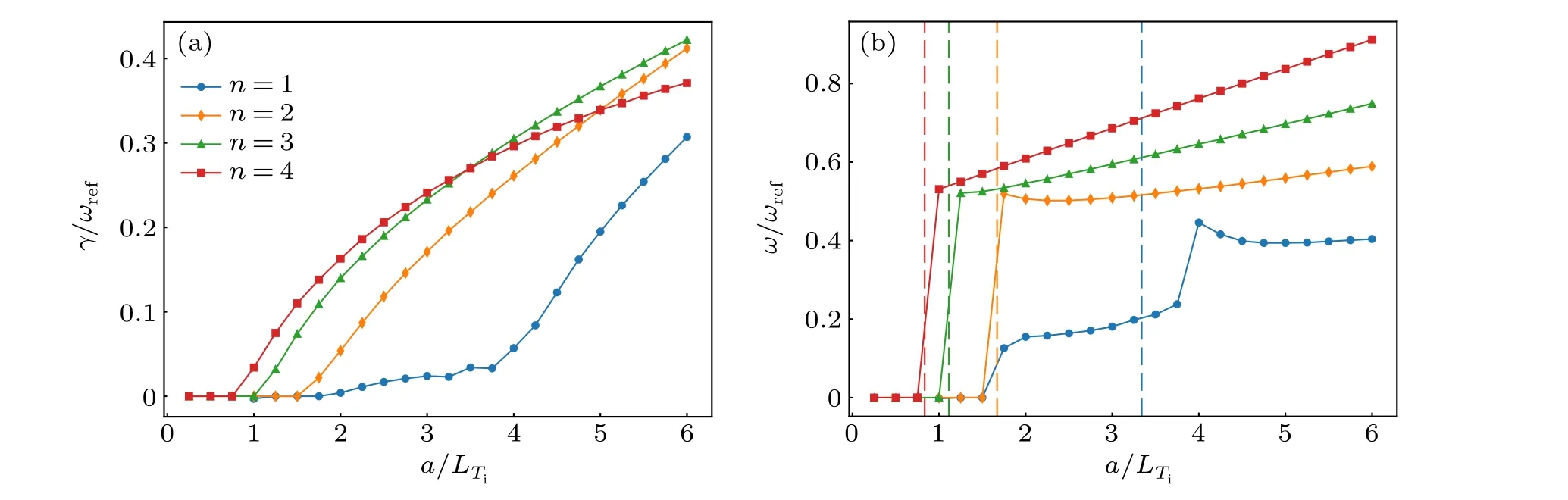
Fig.6.The growth rate(a)and frequency(b)of the GENE when a/LTi is scanned for modes from n=1 to n=4 using s-α geometry.The vertical dashed line indicates the critical value calculated using Eq.(12).The same color indicates the same mode number n.

Fig.7.(a) The KBM branches and BAE branches, i.e., lines marked by squares on the left and right, respectively, are shown connected to the continua solutions of the GFLDR marked by circles.To obtain the KBM and BAE branches,δWf is scanned from-0.1 to 0,a/LTi =1.0,3.5 and 5.0 are chosen and Eq.(10)is solved.To obtain the continua solutions,k‖qR is scanned from 0 to 0.1 and Λ =±k‖qR is solved.(b1)The growth rates of the GENE result and that of the BAE/KBM branch near accumulation points are shown when a/LTi is scanned.(b2)Same as(b1)but frequencies are shown.

3.2.The case with fast ions

When fast ions are included in the GENE simulations,the growth rates reduce over the wholekyspectrum as shown in Fig.2.It is clarified in the following that the reduction of the growth rate in the ITG region is ascribed to fast ion dilution effects through direct comparison with the dispersion relation derived from GENE equations.

In order to simplify the gyrokinetic Vlasov equation(Eq.(1)) and derive a dispersion relation suitable for the description of the fast ion dilution effect,the so-called‘local kinetic limit’,[21]i.e., the assumption that fluctuation fields are well localized nearz=0, is introduced.Hence, thezderivatives of fluctuation terms can be replaced by the parallel wave number

correspond to the diamagnetic frequency and the magnetic drift frequency respectively.Neglecting the collisional effect and parallel magnetic fluctuations for simplicity,equation(15)is combined with the quasi-neutrality condition

It can be easily shown that by settingβe=0,equation(21)is reduced to the dispersion relation of the ITG mode in the electrostatic limit derived Ref.[21].As will be shown below, the frequencies and growth rates of the high-nmodes(n=16 for example)in our case can be reproduced by this dispersion relation with a small relative error,so we confirm that the dominant modes in the range of 0.2＆lt;ky＆lt;1 in Fig.2 are typically ITG modes.Once the parallel wave numberk‖is chosen,the eigenvalueωcan be numerically solved by combining Eqs.(21) and (22).In order to determinek‖and make direct comparison with GENE simulations,the eigenmode structures here,i.e.,the shapes of normalizedφ1andA1‖,are assumed to be similar to those in the above case without fast ions.Then,k‖is determined by solving Eq.(15)without fast ions and kept unchanged afterwards.Under this assumption,the dispersion relation can be obtained by setting the determinant of the combination of Eqs.(21) and (22) to be zero.Focusing on the high-nmodes, for example takingn=16 (kyρref=0.5) for the HL-2A case, when the fast ion fraction is increased from 0 to 0.3, the growth rates solved from Eqs.(21) and (22) are shown in Fig.8 and compared with results of GENE simulations.In order to rule out the contribution of fast ions,Pmfiare forced to be zero and the results are shown by dashed lines in Fig.8.Two cases may be of interest.Case 1 keeps both the density gradienta/Lnfiand temperature gradienta/LTfiof fast ions at low values, i.e., the same gradients as in Table 1.Meanwhile, case 2 uses relatively high values for the fast ion gradients, i.e.,a/Lnfi=1.4 anda/LTfi=4.0.As can be seen in Fig.8, the results of GENE simulations and the solutions of dispersion relation match well with each other.The relative errors are under 10%, which may mainly result from the neglect of collision effects and parallel magnetic fluctuation in the derivation of the dispersion relation.The fast ion dilution effect can be explained by comparing the dashed lines with solid lines as well as case 1 with case 2 in Fig.8.It can be seen for the cases with low fast ion gradient that the contribution of fast ions is nearly negligible.The change in thermal ion density is responsible for the reduction in the growth rate with increasing fast ion density.The same dependence can be checked from Eqs.(21) and (22).Characterized by its high temperature and low density,the fast ion effect influences the dispersion relation via a small factornfi/Tfi.Hence,when the fast ion gradient as the driving force inPmfiis not large enough,Pmfi·nfi/Tfiare negligible and fast ions govern the dispersion relation mainly by changing the thermal ion parameters rather than by themselves.

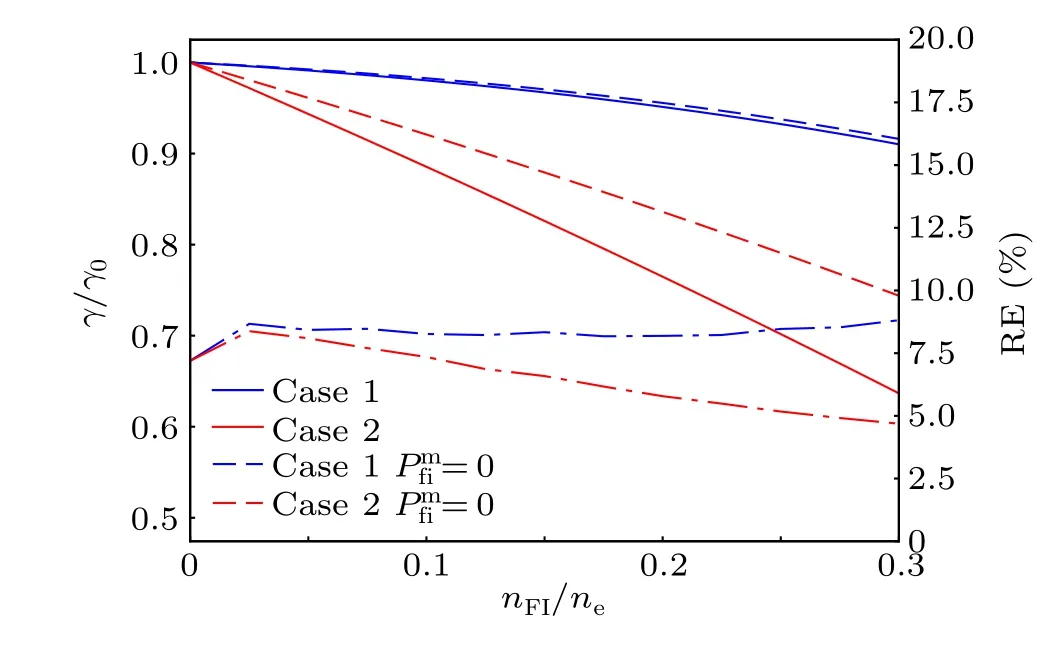
Fig.8.The growth rates solved by the determinant of Eqs.(21) and (22)for case 1 and case 2 are shown by blue and red solid lines respectively,and normalized to the growth rate of the case without fast ions.The dashed lines show the solutions when fast ion contributions are ruled out.The dotteddashed lines show the relative error(RE)between the complex solutions of our dispersion relation and the results of GENE simulations with the same parameters.

4.Summary

In this work,low-nAlfv´enic modes,which are frequently observed in fast-ion-relevant tokamak discharges,were investigated numerically in HL-2A NBI-heated plasma.The local version of the GENE code was employed to perform simulations on the linear stability of NBI-heated plasma.Highfrequency electromagnetic low-nmodes were observed in the simulations of HL-2A plasma excluding fast ions.By comparing comprehensive linear GENE simulation results with the solutions of the general fish-bone-like dispersion relation derived in Ref.[13],it was found that their linear stability properties match well with the BAE branch of the shear Alfv´enic spectrum.By investigating the mode structure and scanning numerical parameters, it has been shown that these low-nmodes are destabilized only by a large ion temperature gradient combined with relatively weak magnetic shear.In the case including fast ions, a finite reduction in the growth rate was observed over the wholekyspectrum.By solving a dispersion relation derived directly from simplified GENE equations, it was demonstrated that the linear stabilization role of fast ions on the ITG mode can be ascribed to the dilution mechanism.

Acknowledgments

The authors would like to thank D.L.Yu, K.R.Fang,X.X.He, Z.J.Li, and X.Zhang for their help in providing experimental data from the HL-2A tokamak.Project supported by the National Key Research and Development Program of China (Grant No.2017YFE0301201) and also partially by the National Natural Science Foundation of China(Grant Nos.U1967206 and 11775069).