Graphene metasurface-based switchable terahertz half-/quarter-wave plate with a broad bandwidth

Xiaoqing Luo(罗小青) Juan Luo(罗娟) Fangrong Hu(胡放荣) and Guangyuan Li(李光元)

1Shenzhen Institute of Advanced Technology,Chinese Academy of Sciences,Shenzhen 518055,China

2Guilin University of Electronic Technology,Guilin 541004,China

Keywords: terahertz metasurface,waveplate,graphene,reconfigurable

1.Introduction

Metamaterials and metasurfaces have recently emerged as promising platforms for manipulating the polarization state of electromagnetic waves because of their compactness,flexibility,and easy integration.[1-6]Half-wave plates(HWPs)and quarter-wave plates (QWPs) are two critical devices for realizing polarization conversion among two orthogonal polarization states, and the left- and right-handed circular polarization (LCP and RCP) states.In the terahertz regime,[7]metamaterial-or metasurface-based HWPs/QWPs are of particular interest because conventional approaches based on birefringence or total internal reflection effects are usually bulky,narrowband,and sometimes lossy.

Over the years, metamaterial-based terahertz polarization converters have evolved from narrow-band[8,9]to broadband.[10-15]However, the functionalities of these devices, which are made of metals or dielectrics, cannot be dynamically tuned.Recently, actively switchable HWPs/QWPs based on metamaterials or metasurfaces incorporating tunable materials, such as liquid crystals, vanadium dioxide (VO2),or graphene, have attracted increasing attention.Based on the metamaterials incorporating liquid crystals,Vasi´cet al.[16]and Jiet al.[17]respectively proposed electrically tunable terahertz polarization converters, of which the bandwidths are only 0.056 THz and 0.35 THz, respectively.Based on the VO2-metal metasurfaces,Wanget al.[18,19]demonstrated terahertz QWPs with switchable single or multiple operating frequencies.Nakataet al.[20]demonstrated a switchable QWP operating at the specific frequency of 0.617 THz by designing a VO2-based anisotropic checkerboard metasurface.Zhaoet al.[21]proposed a switchable terahertz metamaterial that can be switched between an HWP and a QWP in the spectral band of 2.09 THz-2.27 THz, corresponding to a relatively narrow bandwidth of 0.18 THz.Quite recently, some of the authors[22]proposed a metal-VO2metamaterial for achieving broadband switchable terahertz HWP/QWP,the bandwidth of which covers 0.66 THz-1.40 THz,corresponding to a relative bandwidth of 71.8%.We further proposed a novel design philosophy making use of the transition from the overdamped to the underdamped resonance,and designed a VO2metal hybrid metasurface for achieving broadband dynamically switchable HWP/QWP in the spectral band of 0.8 THz-1.2 THz.[23]

Compared with liquid crystals and VO2, graphene has many unique characteristics, including ultra-thin thickness(only 0.33 nm), low loss, and continuous and flexible tunability via electric biasing,[24]chemical doping,[25]or optical pumping.[26]Zhanget al.[27]and Tavakolet al.[28]respectively proposed switchable QWPs based on the graphene metamaterials,and showed that the polarization state of the output wave could be dynamically switched among linear, left- and right-handed polarization by changing the graphene chemical potential.Zhanget al.[29]proposed functional switch from a QWP to an HWP within 4.80 THz-5.10 THz based on a graphene metasurface.The corresponding bandwidth is only 0.3 THz and the relative bandwidth is only 6%.Guanet al.[30]proposed a hybrid graphene-dielectric metasurface for realizing switchable HWP/QWP operating at the single frequency of 1 THz.Qiet al.[31]also proposed a graphene-based highefficiency switchable HWP/QWP operating at the specific frequency of 15.96 THz.Quite recently,Zhanget al.[32]proposed a hybrid graphene-metal metasurface for achieving terahertz HWP/QWP in the frequency range of 1.38 THz-1.72 THz.However, the corresponding bandwidth is 0.34 THz and the relative bandwidth is only 22%.Therefore, it remains challenging to design broadband switchable QWPs/HWPs based on graphene metasurfaces,greatly hindering their practical applications.

In this work, we propose a graphene-metal hybrid metasurface for achieving broadband switchable terahertz HWPs/QWPs.The metasurface unit cell is composed of a gold stripe and a graphene stripe on a thick gold film sandwiched by a dielectric spacer.We will show that the function of the proposed metasurface can be switched from a broadband HWP with polarization conversion ratio (PCR) exceeding 97%in the band of 0.7 THz-1.3 THz,to a broadband QWP with ellipticity over 0.92 in the range of 0.78 THz-1.33 THz.Therefore,these two switchable functionalities share the same spectral band of 0.78 THz-1.3 THz,corresponding to a strikingly broad bandwidth of 0.52 THz and relative bandwidth of 50%,which is much larger than those of graphene-based metasurface HWPs/QWPs in the literature.[29-32]

2.Results and discussion

2.1.Simulation setup

Figure 1 illustrates the proposed metasurface acting as a broadband and dynamically switchable terahertz HWP/QWP.The metasurface unit cell consists of a gold short stripe and a graphene long stripe, which are perpendicular to each other and placed at a 45°tilt with respect to thex-axis.These graphene-gold hybrid stripes stand on a thick gold film sandwiched by a polyimide spacer, forming a metal-insulatormetal configuration.The metasurface can be fabricated using the state-of-the-art top-down microfabrication process.A thick gold film is first deposited onto a silicon substrate, followed by spin-coating of a polyimide film of the designed thickness.A monolayer graphene layer is then transferred on the top, and patterned into two-dimensional array of stripes using photolithography and reactive ion etching.Finally, the gold stripe array can be fabricated via photolithography,thermal evaporation,and liftoff processes.[33]

The operation principle of the proposed metasurface is as follows.When the Fermi level of grapheneEFis pinned at 0 eV, the graphene conductivity is as low as the dielectric material for the terahertz wave.In this scenario,the metasurface unit cell is effectively composed of the gold stripe, thus the metasurface works as an HWP which can convert the incident linear polarization state into the orthogonal linear polarization state.When the graphene Fermi level is tuned toEF=1 eV, which can be done via external stimulus, such as electric biasing[24]or optical pumping,[26]the graphene conductivity is as high as metal-like material.In this case, the metasurface acts as a QWP that converts the linearly polarized incident wave into a circularly polarized wave.

Fig.1.Schematics of the proposed graphene-metal hybrid metasurface.(a)3D view of the meta-surface,which can function as an HWP converting the incident linearly y-polarized terahertz wave into an x-polarized wave when the Fermi level of graphene EF is 0 eV,or as a QWP converting the incident y-polarized wave into a right-handed circularly polarized wave when EF =1 eV.(b) Top view of the unit cell with Λ =120 µm,WAu=30µm,WG=20µm,L=90µm,hPI=38µm,and hAu=200 nm.

The polarization-dependent reflection amplitude and phase spectra of the proposed metasurface were numerically simulated using the frequency-domain solver in CST Microwave Studio.The unit cell boundary conditions were applied in thexandydirections, and the open boundary condition was used in thezdirection.Tetrahedral meshes with adaptive refinement process were applied.In the all simulations, gold was modelled using the lossy metal model with conductivity of 4.56×107S/m, and the built-in material permittivity was adopted for polyimide.

The surface conductivity of grapheneσGcan be described by the Kubo equation with intraband and interband contributions,[33]that is

According to the Pauli exclusion principle, the interband contribution can be safely neglected compared with the intraband contribution for low terahertz frequencies at room temperature.[34,35]Thus the expression of the graphene conductivity can be simplified into[36]

whereeis the charge of an electron,kBis the Boltzmann constant,Tis the temperature,ωis the light frequency,τis the carrier relaxation time from the impurities in graphene,and ħ is the Planck constant.

2.2.HWP function

Figures 2(a)and 2(b)depict the simulated reflection amplitude and phase spectra of the proposed metasurface when the graphene Fermi level is set to 0 eV, and under the incidence ofu-v-polarized terahertz wave.Results show that|ruu|and|rvv| are almost equal to each other, and are close to 0.9 within the frequency range of 0.7 THz-1.3 THz.Meanwhile,their phase differences are approximately equal to-180°,i.e.,ΔΦ=Φvv-Φuu=-180°.Therefore,the graphene-metal hybrid metasurface withEF=0 eV can act as a broadband and efficient HWP.

Fig.2.Simulated reflection (a) amplitude |r| and (b) phase Φ spectra of the proposed hybrid metasurface with EF = 0 eV under u- and v-polarized incidences.(c) Calculated reflection amplitude spectra for the co-polarization|ryy|and cross-polarization|rxy|.(d)Calculated PCR spectra under y-polarized incidence.Blue regions in panels(b)-(d)indicate the broad operation band of the obtained HWP.

In order to evaluate the performance of the obtained HWP under they-polarized incidence,we calculate the co-polarized and cross-polarized reflection amplitude spectra,|ryy|and|rxy|,and the spectra of the polarization conversion ratio (PCR),which can be calculated by

Figure 2(c) shows that the cross-polarized reflection amplitude|rxy|is larger than 0.9,whereas the co-polarized reflection amplitude|ryy| is smaller than 0.1 in the range of 0.7 THz-1.3 THz.For|ryy|,there exist three dips located at 0.74 THz,0.99 THz,and 1.23 THz.As a result,the calculated PCRs are larger than 0.97 within the broad spectral band of 0.7 THz-1.3 THz.This corresponds to a relative bandwidth of Δf/f0=60%with the central frequency located atf0=1 THz.These results suggest that the incidenty-polarized terahertz wave can be efficiently converted to thex-polarized wave by the reflective metasurface with a broad operation bandwidth and high polarization conversion ratios.In other words, the proposed metasurface can work as a broadband and efficient HWP if the graphene Fermi level is 0 eV.

The broadband performance of the obtained HWP can be understood from the surface current distributions on the gold and graphene stripes and on the bottom gold film.Figure 3 depicts the surface current distributions under theuandv-polarized incidences at the three resonant frequencies off= 0.74 THz, 0.99 THz, and 1.23 THz, for which|ryy|shows dips,as shown in Fig.2(c).Figures 3(a)and 3(b)show that at 0.74 THz, the surface currents on the gold stripe are weak under theu-polarized incidence,but strong under thevpolarized incidence.These strong surface currents have opposite directions compared to those on the bottom gold film,producing a magnetic resonance under thev-polarized incidence.Similarly, at 0.99 THz and 1.23 THz, Figs.3(c) and 3(e) show that magnetic resonances are also generated under theu-polarized incidence,because the surface currents on the gold stripe have opposite directions to those on the gold film.Figure 3(d) shows that for thev-polarized incidence at 0.99 THz,the surface currents on the gold stripe are strong and have clear flow direction,whereas those on the gold film have counter-propagating directions and almost cancel each other.At 1.23 THz,the surface currents on the gold stripe and on the gold film are parallel to each other, resulting in an equivalent electric resonance,as shown in Fig.3(f).Therefore,the broadband performance of the obtained HWP should originate from the superposition of these multiple resonances.

Fig.3.Surface current distributions(arrows for directions and colors for strengths)on the gold and graphene stripes(1st and 3rd columns)and on the gold film(2nd and 4th columns)for three resonant frequencies of(a)and (b) 0.74 THz, (c) and (d) 0.99 THz, (e) and (f) 1.23 THz when the graphene Fermi level is EF =0 eV.The 1st and 2nd columns are for the u-polarized incidence,and the 3rd and 4th columns are for the v-polarized incidence.The black arrows indicate the dominant current directions.

2.3.QWP function

We now tune the graphene Fermi level toEF=1 eV.Figure 4(a) shows that the reflection amplitudesruuandrvvare close to 0.9 for frequencies above 0.80 THz.Therefore,ryyandrxyare also close to each other,and their phase differences are approximate to-270°within the broadband frequency range of 0.78 THz-1.33 THz,as shown in Figs.4(b)and 4(c).These results suggest that the proposed metasurface withEF=1 eV now acts as a terahertz QWP.

The performance of the obtained QWP can be quantified using the ellipticity defined asχ ≡S3/S0, where the Stokes parametersSandS3are expressed as[12]

where ΔΦ= ΔΦyy-ΔΦxymeans the phase difference between co-polarization and cross-polarization reflections.Whenχequals to 1 or-1, the polarization state of the reflective terahertz wave is LCP or RCP, respectively.Figure 4(d)shows thatχ＆gt;0.92 over the broad frequency range is 0.78 THz-1.33 THz.This result means that the graphenemetal hybrid metasurface withEF=1 eV now functions as a broadband and efficient QWP that converts the incident linearypolarization into the RCP.

Fig.4.Simulated reflection(a)and(b)amplitude|r|and(c)phase spectra of the proposed hybrid metasurface with EF=1 eV.(d)The calculated ellipticity under linearly y-polarized incidence.Blue regions in panels(b)-(d)indicate the broad operation band of the obtained QWP.

To understand the broadband performance of the obtained QWP,we also plot the surface current distributions on the gold and graphene stripes and on the bottom gold film.Here we use the three frequencies 0.7 THz, 1.23 THz, and 0.97 THz,which correspond to two peaks and a dip in the|rxy| spectra, respectively,as shown in Fig.4(b).Figures 5(a)and 5(b)show that at 0.7 THz, the surface currents on the gold and graphene stripes have the opposite direction compared with those on the gold film,forming magnetic resonances for both theu- andv-polarized incidences.For theu-polarized incidence at 0.97 THz, and for both theu- andv-polarized incidences at 1.23 THz, the surface currents on the gold and graphene stripes and on the gold film have the same directions, resulting in equivalent electric resonances, as shown in Figs.5(c), 5(e), and 5(f).For thev-polarized incidence at 0.97 THz, Fig.5(d) shows that the surface currents on the gold and graphene stripes are strong and have well defined directions, whereas those on the gold film are weak and have counter-propagating directions.Therefore,the broadband performance of the obtained QWP should also originate from the superposition of multiple resonances.

Fig.5.Similar to Fig.3 but for(a)and(b)0.7 THz,(c)and(d)0.97 THz,and(e)and(f)1.23 THz when EF=1 eV.

2.4.Effects of key parameters

Figure 6 shows the metasurface performances as the graphene Fermi levelEFvaries continuously from 0 eV to 1.2 eV.The reflection amplitude keeps nearly unity for the all graphene Fermi levels within 0.7 THz-1.2 THz,which guarantees high converting efficiency.Figure 6(c)shows the absolute phase difference|ΔΦ|depending onEF.We note that there is a relatively homogenous region with gradual and continuous phase revolution, lying between about 0.7 THz and 1.1 THz.In this spectral region, the|ΔΦ| evolves continuously from about 180°to 90°whenEFincreases from 0 eV to 1 eV.In addition, asEFfurther increases to 1.2 eV,|ΔΦ| approaches 80°.Thus, our numerical results show a robust tolerance of the proposed metasurface.

The influence of the PI thicknesshPIis shown in Fig.7.The reflection amplitude components|ruu|and|rvv|are almost unity for differenthPIfrom 34 µm to 42 µm and different graphene Fermi energies.In contrast, the absolute phase difference|ΔΦ|exhibits distinct dependency onhPIas shown in Figs.7(c)and 7(f).ForEF=0 eV,we note that the area of concerned frequency region(about 0.7 THz-1.3 THz)in Fig.7(c)could be divided into two subareas (about 0.7 THz-1 THz and 1 THz-1.3 THz),the former manifests that|ΔΦ|increases while the latter manifests that|ΔΦ| decreases ashPIchanges from 34 µm to 42 µm.WhenhPIequals 38 µm, the|ΔΦ| is about 180°in both subareas(i.e., working as an HWP within 0.7 THz-1.3 THz).ForEF=1 eV, the absolute phase difference|ΔΦ|changes gradually from about 76°to 97°ashPIchanges from 34µm to 42µm.WhenhPIequals 38µm, the|ΔΦ|is about 90°(i.e., working as a QWP within 0.78 THz-1.33 THz).

Fig.6.(a) Reflection amplitude |ruu|, (b) reflection amplitude |rvv| and (c) absolute phase difference |ΔΦ| as the graphene Fermi level varies continuously from 0 eV to 1.2 eV.

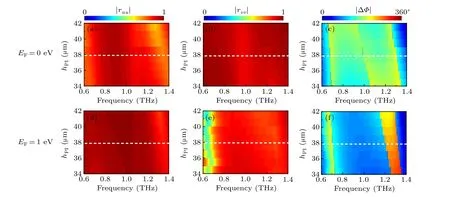
Fig.7.Device performances dependent on the thickness hPI.(a)-(c) Reflection amplitude |ruu|, |rvv|, and absolute phase difference |ΔΦ|when EF =0 eV.(d)-(f)Reflection amplitude|ruu|,|rvv|,and absolute phase difference|ΔΦ|when EF =1 eV.The dashed white line indicates hPI=38µm.

3.Conclusion

In conclusion,we have proposed a broadband switchable terahertz HWP/QWP based on a graphene-metal hybrid metasurface.Simulation results have shown that, by varying the Fermi energy of graphene from 0 eV to 1 eV, the function of the reflective metasurface can be switched from an HWP,which converts the incidenty-polarized terahertz wave into anx-polarized wave,to a QWP that converts they-polarized wave into a right-handed circularly polarized wave.The polarization conversion ratio of the obtained HWP exceeds 97%over a wide band ranging from 0.7 THz to 1.3 THz, and the ellipticity of the obtained QWP is larger than 0.92 over 0.78 THz-1.33 THz.Therefore,we have shown that the proposed metasurface can function either as an HWP or as a QWP in the spectral band of 0.78 THz-1.3 THz.This corresponds to a strikingly broad bandwidth of 0.52 THz and relative bandwidth of 50%,which is much larger than the literature on the graphene-based metasurface HWPs/QWPs.The broadband properties have been explained with the superposition of multiple resonances.We expect the designed broadband and dynamically switchable terahertz HWP/QWP will find applications in the terahertz polarization-dependent systems of sensing,imaging,and telecommunications.

Acknowledgment

Project supported by Shenzhen Research Foundation(Grant No.JCYJ20180507182444250).