基于融合特征与GA-SVM算法的脑疾病基因预测

谭卓昆，罗龙飞，王顺芳

云南大学 信息学院，昆明 650500

近年来，脑部疾病率逐年上升，给人类身心健康和社会带来了巨大影响及负担[1]。大脑疾病通常可能是由一个或一组基因的故障引发的，而识别脑部疾病基因不仅在实验上发现疾病基因具有重要的指导意义，并且对于理解脑部疾病机制和研发药物也至关重要[2]。

本文以此为契机，对脑部相关疾病基因的预测展开研究。在此之前，有不少的学者也进行了探究。Zhang和Gao等人[3-4]的综述文章中提到，不同数据构建的网络提供的特征信息是不一致的，多网络集成的方法可以融合多个数据网络的特征，把各网络的优势集中起来，克服单一网络特征种类不足的限制。秦小麟[5]使用多种基于脑功能超网络特征进行脑疾病基因的分类实验，将具有脑部信息的相关特征加入了进来，效果明显提升，但是文中却未曾考虑蛋白质相互网络（protein-protein interaction networks，PPI）与脑部基因预测之间的关联性。胡春荣等人[6]对脑源性神经营养因子作用的PPI功能进行分析，证明了PPI与大脑调控、发育是有密切关联的。Ye等人[7]基于Mashup中矩阵分解的不同数据源构建的多个网络中获取基因的特征表示，进而预测老年化疾病的相关基因，但是却未结合老年化疾病中与脑部信息相关联的特征信息。在上述学者的研究中，主要的不足之处是使用单一的分子相似性网络或结合相关的基因网络预测脑部相关的疾病基因，导致特征种类及信息受限，从而使最终的实验效果欠佳。因此，本文将PPI和大脑连接组信息结合，进一步丰富特征种类及信息。

随着技术的进步，融合多网络的方法不断迭代更新，Gligorijevic和Peng等人[8-9]使用深度神经网络的方式对不同PPI以及疾病特异性基因的相似性网络进行融合操作，对此两位学者分别提出了DeepNF和DeepMNE-CNN的方法。深度神经网络可以很好地挖掘生物网络的特征信息，但是普遍耗时长，构建的生物网络较小时，极易出现过拟合，并且两者使用的方法中未把已知的先验信息进行结合，对此本文使用半监督的自编码器解决上述方法的不足。此外，Wang等人[10]提出了一种名为brainMI的模型，利用堆叠半监督自编码器融合不同数据源的网络，预测脑部疾病基因，虽然考虑到了不同数据网络的互补关系，但是并不全面，没有将基于共表达数据的PPI相似性网络加入实验，并且未对预测模型超参数进行优化处理。对此，本文不仅在实验中加入了融合基于共表达数据的PPI，还增加消融实验对其必要性和有效性进行验证，并且在设置模型超参数时，提出使用遗传算法进行全局寻优，求解最优参数，进而得到最佳预测模型。

综上所述，在融合多网络特征方面，本文首先构建了基于大脑连接组数据的基因网络，以及基于共表达数据、基于实验数据、基于数据库数据的PPI共四种相似性网络，然后利用重启随机游走算法（random walk with restart，RWR）提取每一网络的特征信息，最后使用半监督自动编码器进行处理及融合。在模型优化方面，为了提高脑部相关疾病的预测效果，本文根据脑疾病基因的预测结果对不同的分类器进行筛选，得到最佳效果的分类器，即支持向量机（support vector machine，SVM）模型。并且在模型的优化上，提出了GA-SVM算法，利用遗传算法对SVM进行优化，进一步提升模型对脑部疾病基因的预测性能。

1 多网络特征融合策略

将来自不同数据源的多个网络的特征进行融合，可以结合每个网络的优势，克服单个网络的特征信息不足的基本限制，同时也为模型提供更为丰富的输入特征，提高脑疾病基因的预测效果[11]。本文的多网络融合策略以单个数据网络的特征提取为基底，使用半监督自编码器对不同网络的特征进行编码操作获取有效特征，然后根据设定的筛选规则选出约束特征，并结合经过解码操作的重建特征得到单个网络特征，最终将每个网络的特征融合成全局特征。

1.1 单个网络的特征提取

单个生物数据网络特征提取效果的优劣，往往影响着最后融合的全局特征，本文选择的是RWR算法，相比于传统的随机游走（random walk，RW）算法，多了一个回到初始节点的选择。RWR算法不仅可以捕获网络节点之间的全局相关性，而且可基于高维网络全局结构信息，提取节点特征表示，可以很好地满足实验的需求[12]。其中单个网络可表示为G=(V,E)，H表示网络G的邻接矩阵，重启随机游走过程可表示为式（1）：

其中，α为重启概率，T为转移概率矩阵，ei为初始的节点特征向量，Pi(t)为节点i游走t步后的特征表示。另外Tij为节点i到节点j的转移概率。Tij的计算如式（2）所示：

其中，Hikj表示从节点i到节点j的邻接矩阵值，k表示游走的步数。最终对需要提取特征的网络的邻接矩阵H使用RWR算法，就能利用网络的全局结构信息得到节点的特征表示。此外，该算法只包含一个固定参数重启概率α，本文在不同α取值的情况下，对提取单个网络特征的效果进行探究。

1.2 融合多网络特征

在融合多网络时，首先利用RWR算法学习单个网络的特征表示，再使用基于半监督自编码器中的编码操作对每个网络提取有效特征，然后选取皮尔逊相关系数（Pearson correlation coefficient，PCC）大于0.5的基因对作为约束特征并结合经过解码操作的重建特征得到单个网络的特征表示，最后将每个网络的特征融合成全局特征。

在本文中，半监督自编码器主要由编码器和解码器两部分组成，相比于无监督的自编码器，虽然本质上都是三层神经网络，但半监督自编码器可以将许多不利于最终目标预测的无关信息忽略，并且提取与目标关联性较高的特征，保证提取的网络特征与脑疾病基因的相关性，从而提升模型最终的预测性能[13]。编码器通过编码操作可将输入数据的高维特征表示编码为有效特征h，其训练过程见式（3）：

其中，W表示数据输入层到低维有效特征输出层的权重矩阵，x为输入数据，b为偏置向量。解码器的效果则与编码器相反，可以将提取的有效特征重建为输出数据z，其训练过程见式（4）：

式中，W′为隐藏层到输出层的权重矩阵，b′为偏置向量。半监督自编码器的损失函数如式（5）所示：

式中，N表示样本数，ypre为目标的预测值矩阵，λ为调整权重系数。此外，生物信息学中通常还利用PCC值来度量基因间的相似性，然后基于两两基因之间的PCC排序，为了方便实验，本文选取PCC>0.50的基因对作为约束特征。PCC计算基因之间的相似性公式如式（6）所示：

其中，gi、gj分别表示基因i和基因j。对基于大脑连接组的基因相似性网络，以及基于PPI相关的另外三个相似性网络的特征融合流程如图1所示。

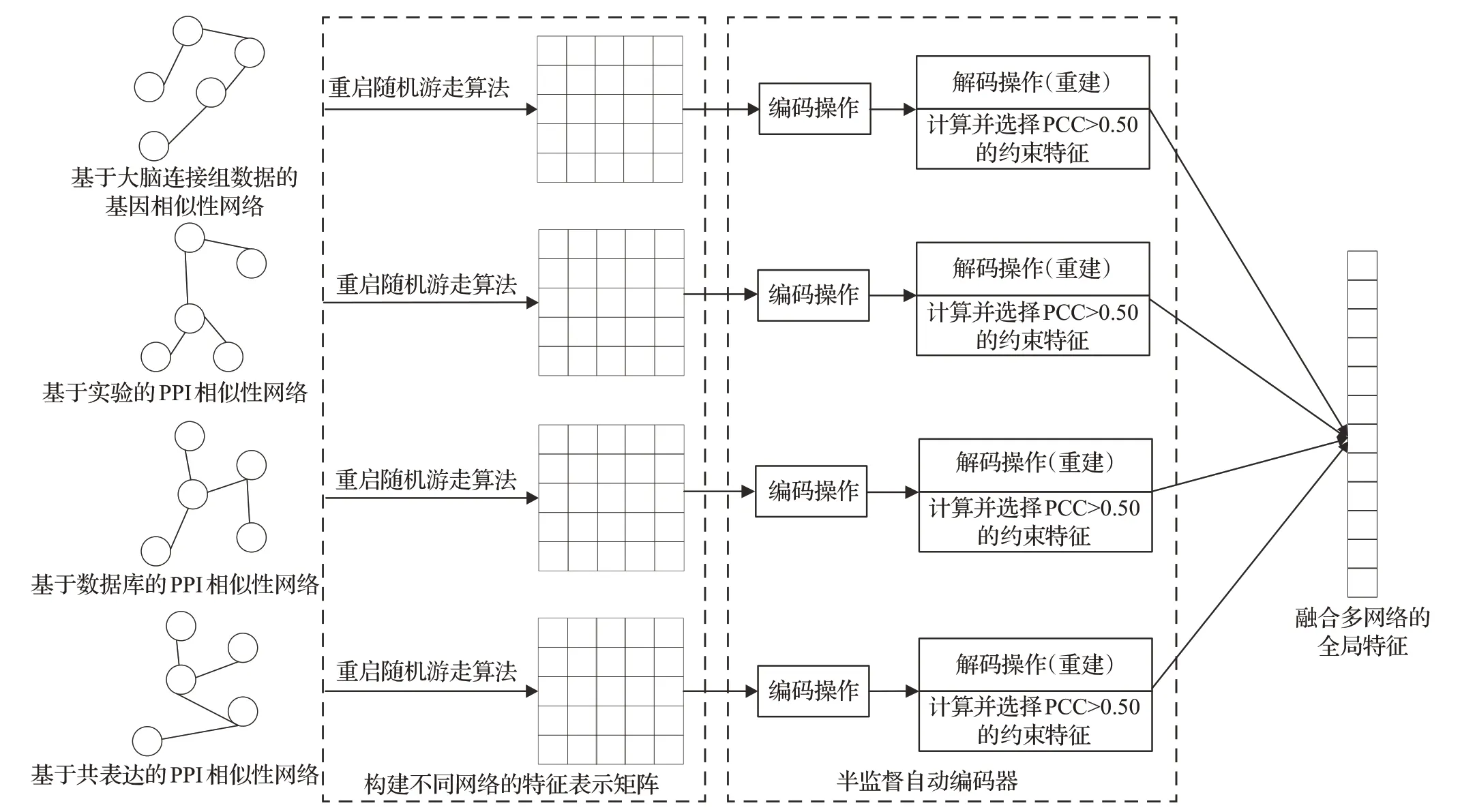
图1 多网络的特征融合流程Fig.1 Feature fusion process of multi-networks

2 GA-SVM算法优化策略

为了提升模型在脑疾病基因预测的性能及效果，本文使用GA-SVM算法对模型的关键超参数进行求解。GA-SVM算法是以径向基核函数（radial basis function，RBF）的SVM模型为基底，使用遗传算法对SVM模型的惩罚系数C、gamma值进行全局寻优，提升模型的预测性能。

2.1 遗传算法

遗传算法（genetic algorithm，GA）是模拟达尔文生物进化论的自然选择和遗传学的生物进化过程的计算模型，通过模拟“优胜劣汰，适者生存”的进化法则，搜索最优解个体，主要操作为选择、交叉和变异。此外，GA具有并行性、通用性、全局性和鲁棒性特点，为最稳健和有效的全局优化求解算法，广泛应用于模型参数优化等全局优化的场景之中，效果显著[14]。因此，本文将GA应用于模型的优化上，提高脑部疾病基因的识别效果。

2.2 GA优化SVM模型

SVM是目前最常用、效果最好的分类器之一。SVM分为线性可分和非线性可分，其基本原理是将低维空间的样本训练数据映射到高维空间中，使得样本训练数据线性可分，进而对边界进行线性划分，由于分类器仅由支持向量决定，SVM能够有效避免过拟合，以及具有优秀的泛化能力。

在非线性分类任务中，SVM关键在于将输入空间中线性不可分的样本映射到线性可分的特征空间中。而特征空间的好坏直接影响到了SVM的效果，因此，本文选择RBF的SVM进行分类实验，该核函数对于处理类标签和样本属性之间是非线性关系的状况具有很好的性能。RBF自带的一个参数σ，不仅隐含地决定了数据映射到新的特征空间后的分布，还影响模型训练与预测的速度，其与模型的输入参数gamma的关系见式（7）：

因此使用遗传算法对gamma及惩罚系数C寻优求解。本文提出的GA-SVM算法优化策略就是将SVM模型的gamma和C作为初始种群，不断的迭代进化，寻找出全局最佳的gamma和C值，实现对SVM模型的优化，优化流程如图2所示。

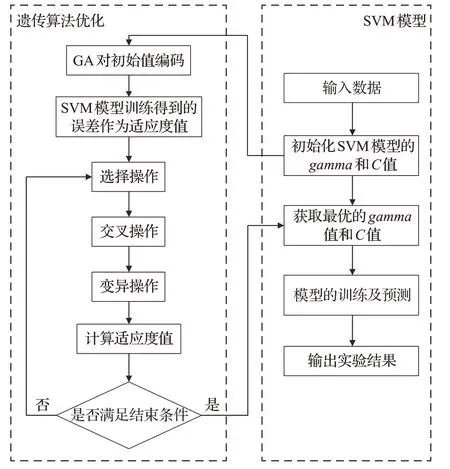
图2 GA-SVM算法优化流程Fig.2 GA-SVM algorithm optimization process

2.3 结合全局特征的优化预测算法步骤

在实验时，首先要构建单个的生物数据网络，通过RWR算法分别提取每个网络的特征表示，再基于半监督自编码器使用编码操作将提取每个网络的有效特征，然后将筛选出的约束特征结合经过解码操作的重建特征提取单个网络的特征，最后将每个网络的特征融合，具体操作见图1。然后是构建GA，并对SVM模型的gamma和C值进行全局寻优求解，获取最优模型后根据融合后的全局特征作为输入，预测脑部疾病基因，具体操作见图2。

以融合多网络后的全局特征作为输入，并利用GASVM算法模型的脑疾病基因预测总流程如图3所示，流程解释如下：

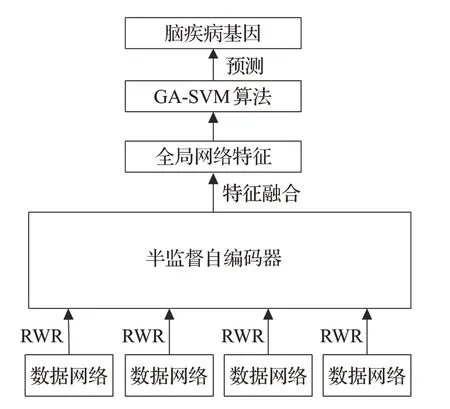
图3 脑疾病基因预测实验流程Fig.3 Brain disease gene prediction experimental process

步骤1从不同数据源获取原始的生物数据，对数据进行标准化、填充等处理，然后构建四种生物数据网络。

步骤2构建重启游走算法，并在步骤1得到的四个生物数据网络中，分别使用重启随机游走算法捕捉每一个网络的节点特征表示，最后得到四个网络的特征表示矩阵。

步骤3使用半监督自编码器对四个生物网络的特征表示矩阵进行下一步处理，具体操作如下：

（1）通过编码操作提取网络的有效特征；（2）计算脑疾病基因之间的PCC，筛选约束特征，然后对网络有效特征进行重建处理；（3）重建特征与约束特征结合生成单个网络的特征表示。

最后将每个网络的特征表示进行融合，即为预测脑部疾病所需的全局特征。

步骤4使用GA-SVM算法对模型参数进行全局寻优，在获得最佳gamma和惩罚系数C后，赋值于相应的模型参数，然后得到最佳的预测模型。

步骤5在得到最佳的预测模型后，利用四种生物网络特征融合的全局特征作为输入，即可进行脑部疾病基因预测。

3 实验结果及分析

3.1 实验环境介绍

本文的全部实验均在Window 10操作系统下完成，所有的代码均使用Python编程语言实现，并在PyCharm集成开发环境下进行编写与调试，实验所使用的软件环境和硬件环境的相关信息分别如表1与表2所示。

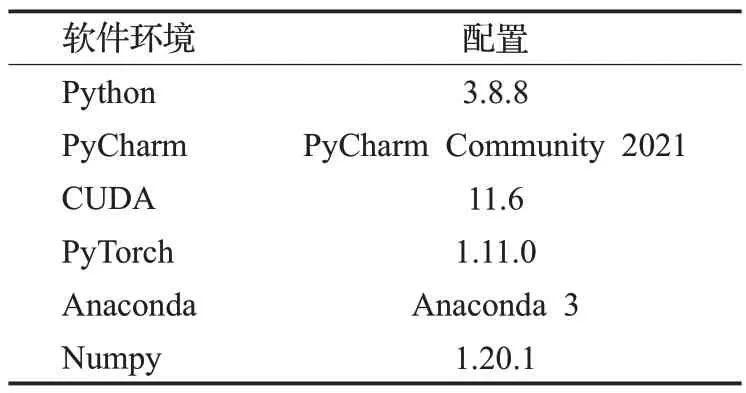
表1 实验软件环境Table 1 Experimental software environment

表2 实验硬件环境Table 2 Experimental hardware environment

3.2 数据集

本文在构建基于大脑连接组的基因网络时需要从The Human Connectome Projec（tversion S1200）提供的数据平台下载R-fMRI数据，并结合Wang和Ji等人[10，15]做的脑部功能映射研究构建网络，而构建基于实验、数据库的蛋白质相互作用网络，以及基于共表达的蛋白质相互网络的数据则需要从STRING数据库（version 11.0）获取并导出相应的网络，STRING数据库主要搜索已知蛋白质之间和预测蛋白质之间相互作用，是目前覆盖的物种最多，信息最丰富的蛋白质相互作用网络数据库[16]。此外，脑部疾病基因的数据来自于Schriml等人[17]构建的人类疾病本体（human disease ontology）数据，并且从人类疾病本体数据中筛选人类所有已知的帕金森（Parkinson disease，PD）疾病、严重抑郁症（major depressive disorder，MDD）疾病的相关基因分别作为正样本。而负样本则从融合多网络后的全局特征的标签中进行选择。为了更好地综合评估所提出模型在各数据集上的性能，本文将负样本划分为总负样本和平衡负样本，总负样本为各数据集中除去正样本后的所有样本，而平衡负样本为经过随机抽取与正样本长度相同的样本，以便于克服正、负数据集之间的不平衡现象，进而更好地训练模型。计算PD和MDD数据集的不平衡比分别为10.1和32.6，结果表明为中度不平衡数据集，便于为后续模型评估指标选取提供依据。在整个实验过程中，所用到的人类脑疾病基因数据集如表3所示。

表3 数据集Table 3 Datasets

3.3 评价指标

交叉验证是评估分类模型性能的常用方法。在这项研究中，实验时将数据集分成十个不重叠的大小相等的集合，并在对其余集合进行测试，最后记录平均性能参数。此外，本文通过受试者工作特征曲线（receiver operating characteristic curve，ROC）的下面积（AUC）、准确率（ACC）、F值（F-score）、精度-召回率曲线下面积（AUPR）这四个指标来评价分类模型的整体预测性能，而且在正负样本的二分类实验中AUC和AUPR值越高意味着模型综合预测性能越好。ACC和F-score的计算见公式（8）、（9）。其中TP指原来是正样本，分类成正样本的数量，FP指本来是负样本，却被分类成正样本的数量，TN指原来是负样本，分类成负样本的数量，FN指本来是正样本，却被错误分类成负样本的数量。在绘制ROC图以及计算对应的AUC时，需要计算样本的真阳性率（true positive rate，TPR）和假阳性率（false positive rate，FPR），TPR和FPR的计算见公式（10）、（11）。其中TPR指所有实际为正样本中，被正确判断为正样本的比率，FPR指所有实际为负样本中，被错误判断为负样本的比率。评价样本不平衡性的标准普遍使用不平衡比（imbalance ratio，IR），计算如式（12）所示，其中T和F分别代表正负样本数，当负样本数远大于正样本数时，即可判定为高度不平衡数据集。AUPR在不平衡数据集的模型效果评估上具有良好的性能，因此选用AUPR进行不平衡数据集的评估，计算该指标时需要先计算其中P和R，也就是查准率和召回率，如式（13）和（14）所示。

3.4 分类器选取与实验参数分析

3.4.1 分类器性能评估及选取

为了评价不同分类器在脑部疾病数据集上的性能，本文在PD数据集上通过k折（k=5，10，15）交叉验证实验，最终在使用10折交叉验证实验中获得了最佳模型。因此选择10折交叉验证来进行接下来的比较。评估分类器精度的方法使用ROC曲线图，这是分析分类器整体性能的常用方法。它是将真阳性率描述为假阳性率的函数，在敏感性和特异性之间进行不同的权衡。AUC通常被用作诊断准确性的一种总结性测量。通过对数据集的10折交叉验证测试，将AdaBoost、ANN、BiLSTM、GBDT、MLP、RF和SVM分类器模型的预测结果进行了比较（图4），可以看到SVM模型效果最佳，其AUC值为0.794，相比于其他分类器，优势比较明显。

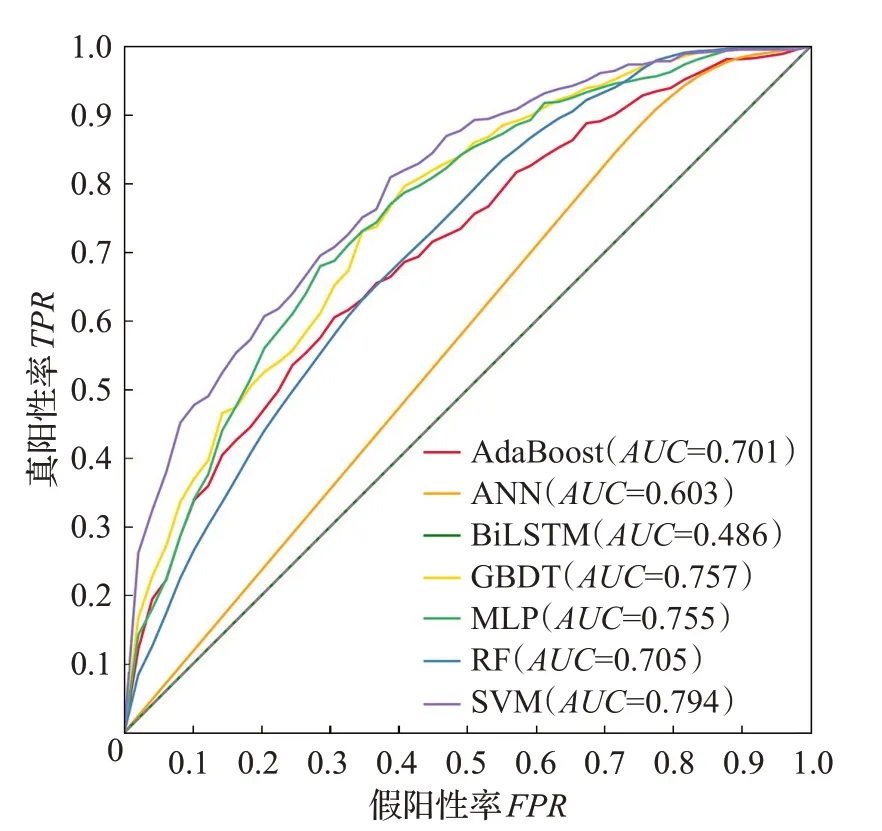
图4 十折交叉验证下的分类器性能分析Fig.4 Classifier performance analysis under 10-fold cross-validation

3.4.2 基于RWR算法的特征融合效果分析

重启随机游走算法是在随机游走算法的基础的改进。算法包含一个参数α为重启概率，1-α表示移动到相邻节点的概率，经过迭代到达平稳，平稳后得到的概率分布可被看作是受开始节点影响的分布。重启随机游走可以捕捉两个节点之间多方面的关系，捕捉图的整体结构信息。重启概率越大，结构相关性对结果的影响越小[18]。因此本文从重启概率大于0.5的RWR算法特征提取效果进行探究，在实验中，首先对半监督自编码器的参数进行设置，学习率设置为0.005，批次大小设置为256，迭代次数设置为1 800次，优化器使用的是Adam，以便于融合各个网络。然后以PD数据集展开实验，结果如表4所示，最终找到最佳的重启概率为0.95。实验结果表明并不是重启概率越大效果越好，而是随着α的变化，疾病基因的总体预测效果先上升后下降，而且α为1时RWR算法就会退化为一般的RW算法。

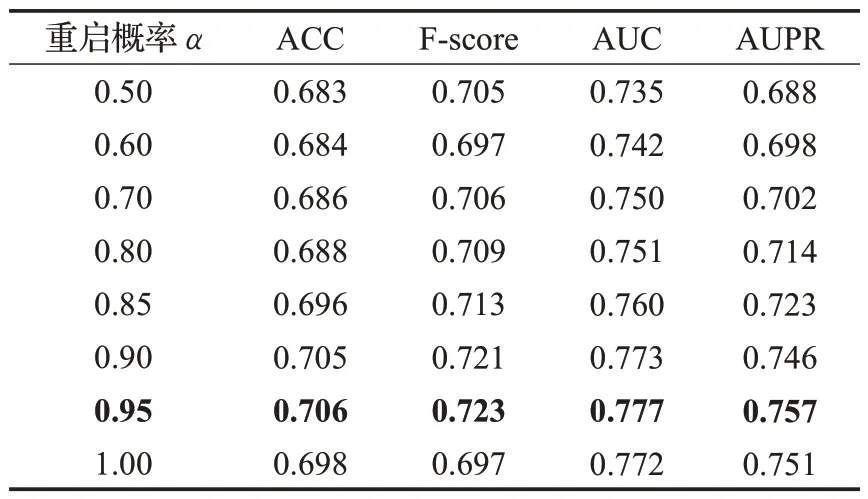
表4 不同重启概率下模型的性能比较Table 4 Performance comparison of models under different restart probabilities

3.4.3 GA-SVM算法的实验参数设置

实验参数的选取会直接影响模型性能，GA-SVM算法的实验参数选取可分为两个部分。首先是设置遗传算法的相关参数，如种群规模、最大迭代次数、变异概率，而且在实验过程中对轮盘选择、排序选择算子、交叉算子、变异算子进行评估，实验结果表明排序选择算子效果优于其他算子，因此设置该算子进行后续的实验。其次是使用构建好的遗传算法对SVM模型的gamma值和惩罚系数C进行全局寻优，求解出最佳的gamma值和C值。在实验中，设定的遗传算法参数以及在PD数据集、MDD数据集中求得SVM模型的最佳参数值如表5所示，并且在参数设置时采取10折交叉验证评估模型性能。

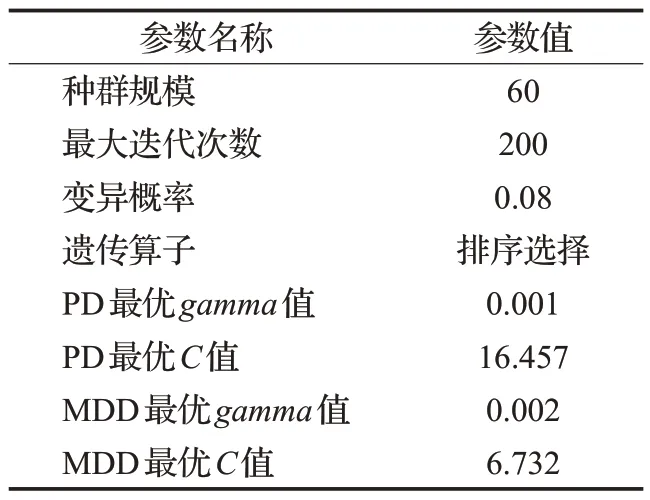
表5 实验参数Table 5 Experimental parameters

3.5 实验对比

3.5.1 在MDD数据集上与其他分类模型比较

为了衡量本文提出的GA-SVM算法模型在预测脑部疾病基因的能力与通用性，使用MDD的数据集训练模型，并且采用了基于10折交叉验证的测试策略，将本文的GA-SVM算法模型与深度学习模型分类器ANN、BiLSTM模型和传统的机器学习分类器AdaBoost、GBDT、MLP、RF模型的预测结果进行了比较（表6）。结果表明，在不同的数据集下相比于其他分类模型，本文模型具有更佳的预测效果。

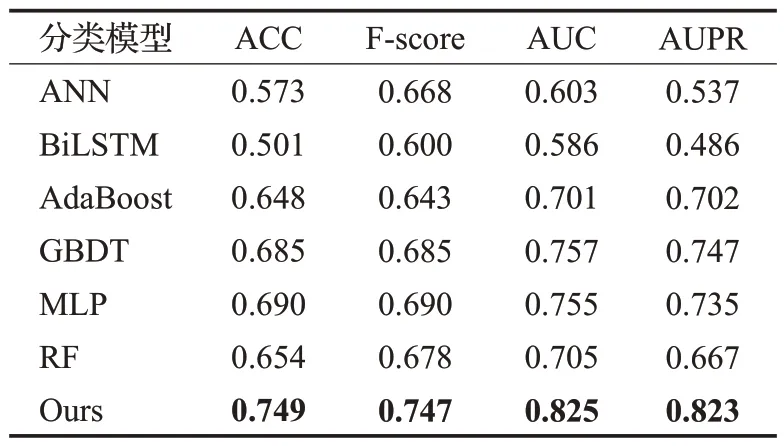
表6 分类模型比较Table 6 Classification model comparison

3.5.2 与现有的疾病基因预测模型对比

在PD数据集、MDD数据集上与现有的其他4种模型（分别是Mashup[7]、DeepNF[8]、DeepMNE-CNN[9]和BrainMI[10]）依次进行了性能比较。实验结果整体表明，相比于其他四种方法，本文的模型对脑部疾病基因的判别更为有效。在PD数据集上的F-score、ACC、AUC、AUPR四个评价指标分别为0.727、0.731、0.805、0.792，除ACC与现有最佳模型持平外，其余指标均有提升，其中AUC值比Mashup、DeepNF、DeepMNE-CNN和BrainMI分别提高了0.048、0.045、0.043、0.018，而AUPR值比其他四种模型提高了0.061、0.051、0.033、0.016。在MDD数据集的测试中分别达到了0.747、0.749、0.825、0.823，各指标比现有模型更好，其中AUC为0.825，比Mashup、DeepNF、DeepMNE-CNN和BrainMI分别提高了0.065、0.059、0.047、0.034，而AUPR值也比其他四种模型分别提升了0.075、0.076、0.065、0.035，效果提升显著。本文提出的模型不仅通用性强，而且从实验结果的AUC和AUPR值来看，对疾病基因的预测精准程度也比其他模型更好，并且能够很好地应用于平衡数据集和不平衡数据集，模型的综合预测性能更为优秀。不同脑部疾病数据集与其他四种模型的性能比较具体如表7所示。

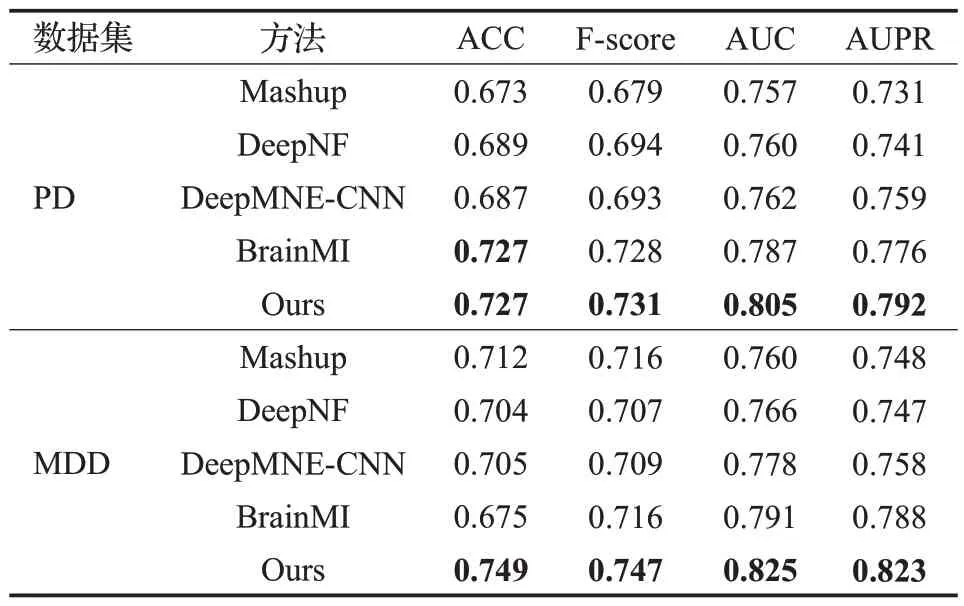
表7 不同模型效果比较Table 7 Comparison of effects of different models

3.5.3 消融实验分析

为了证明研究工作中，多网络融合模块及GA优化SVM模块的有效性，本文使用MDD数据集进行了一系列的对照实验。首先将四个网络的特征单独输入SVM模型，分别观察各网络对脑疾病基因的预测效果，结果表明四个网络中预测效果最好的为基于大脑连接组数据的相似性网络，其ACC、F-score、AUC、AUPR为0.644、0.692、0.713、0.700，以此为基线逐渐叠加模块进行对比。其次是测试融合多网络特征模块提升效果，在使用半监督自编码器进行多网络融合后，ACC、F-score、AUC、AUPR可达到0.706、0.727、0.794、0.796，各项指标均显著提升，说明融合多网络特征对预测疾病基因是十分有效的。最后，在使用多网络融合的基础上，对GA优化SVM模型的效果进行评估，在使用GA后各评价指标可达到0.749、0.747、0.825、0.823，分别提升了0.033、0.020、0.031、0.027，进一步提升了脑疾病基因的预测性能。此外，还对新增加的基于共表达的PPI相似性网络进行评估，在前面提及所有模块进行保留的基础上，对未加入该网络时的疾病预测模型进行测试，得到的ACC、F-score、AUC、AUPR分别为0.697、0.725、0.779、0.766，相比于融合四种网络的全局特征在MDD数据集的预测结果，分别下降了0.052、0.022、0.046、0.057，这证明了本文新增加的数据网络对提升预测效果是有效的。各个模块的消融实验结果如图5所示。

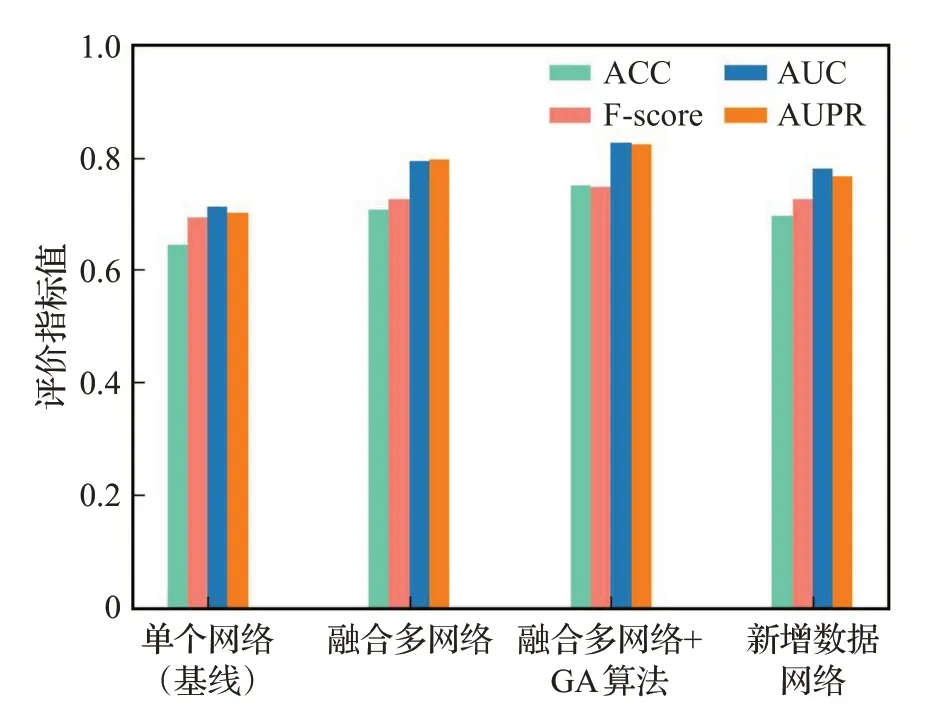
图5 各模块消融实验分析Fig.5 Ablation experiment results of each module

各个模块的评估实验表明，只有把所有的模块及数据结合在一起，才能充分提升预测性能，这也表明了每个数据及模块在预测脑疾病基因模型中的必要性。

4 结束语

本文为了解决单个生物数据网络特征信息受限的问题，通过构建多个生物数据网络，利用重启随机游走算法提取不同网络的节点特征，最后将不同网络的节点特征表示融合为全局特征，有效集成了多个网络的优势。此外，为提高模型在脑疾病基因预测的性能，提出了GA-SVM算法来解决训练时由于相关关键参数影响，而导致模型预测性能不佳的问题。最终的对比实验结果表明，本文模型在预测脑疾病基因上具有更好的预测性能。这项关于预测脑疾病基因的研究也会为未来其他疾病基因的研究提供一个有竞争力的工具。所提出的结合融合多网络特征和GA-SVM算法的脑部基因预测模型也有许多其他潜在的应用，如肝癌疾病基因预测、药物靶点预测等。