深度强化学习求解车辆路径问题的研究综述
杨笑笑,柯 琳,陈智斌
昆明理工大学 理学院,昆明 650000
组合最优化(combinatorial optimization,CO)是运筹学和组合领域的新兴学科。组合最优化问题(combinatorial optimization problem,COP)[1]是一类在离散状态下求极值的最优化问题,在交通、管理决策等领域有着广泛的应用。日常生活中常见的COP问题有旅行商问题(traveling salesman problem,TSP)、车辆路径问题(vehicle routing problem,VRP)、车间作业调度问题(job shop scheduling,JSP)、最小顶点覆盖问题(minimum vertex cover,MVC)、施泰纳树问题(Steiner tree problem,STP)以及装箱问题(bin packing,BP)等。
先前工作中,传统算法是求解COP问题的首要方法。传统算法主要分为三类,精确算法(exact algorithm)[1]、近似算法(approximation algorithm)[1]、启发式算法(heuristic algorithm)[2],详细分类如图1所示。精确算法[1]是指可求出最优解的算法,求解小规模COP问题有较好结果,但在求解大规模COP问题时不能在规定的时间内输出最终的结果;近似算法[1]是指在合理的计算时间内找到一个近似最优解,但较多COP问题无法确定近似比的保证;启发式算法[2]可以根据相关问题快速有效地设计算法,但依赖问题本身,当问题描述发生变化时,需重新设计算法,且可能陷入局部最优解;由于现实世界中具有挑战性的VRP问题通常受到车辆容量、配送中心数量、车辆行驶里程、时间等限制,因此传统算法在应用于现实任务时会有求解速度慢、解质量差等不足[3]。

图1 传统算法分类示意图Fig.1 Schematic diagram of traditional algorithm classification
随着人工智能技术的发展,深度学习(deep learning,DL)[4]在计算机视觉(computer vision,CV)[5]、自然语言处理(natural language processing,NLP)[6]等许多领域取得了突破性的进展。在CV领域[5],DL取代了人类手工设计算法成为了当前的核心算法;在NLP领域[6],DL将NLP从统计模型转到神经网络(neural network,NN)模型,不断学习语言特征,使得在大量特征工程的NLP获得精确的结果;在推荐系统领域[7],DL可以高效地学习用户和项目之间的特征,便于从海量数据中挖掘出匹配关系。作为DL一个重要分支,强化学习(reinforcement learning,RL)和深度强化学习(deep reinforcement learning,DRL)[8]主要应用于序贯决策任务,AlphaGo[9]和AlphaGo Zero[10]围棋算法利用DRL模型结合蒙特卡洛树(Monte Carlo tree,MCT)搜索,成功击败了世界围棋冠军,将DRL的理论和应用研究推向新高度,为利用DRL求解VRP[11]开创全新思路。VRP在离散决策空间进行决策变量的最优选择与RL序贯决策的功能具有天然的相似性,且DRL“离线训练”“在线决策”的特征使VRP在线实时求解成为了可能。
NN解决VRP问题是Vinyals等人[12]将问题类比为机器翻译过程,提出了指针网络(pointer network,PN)模型,使用长短期记忆网络(long-short term memory,LSTM)作为编码器,注意力机制(attention mechanism,AM)[13]作为解码器,从城市坐标中提取特征。但是PN采用监督学习(supervise learning,SL)方式训练网络,需要构造大量高质量的标签,因此大多数研究利用DRL求解VRP问题。除PN模型外,随着图神经网络(graph neural network,GNN)技术的兴起,Scarselli等人[14]利用GNN对每个节点特征进行学习,从而进行节点预测,主要求解思路是利用GNN对节点特征进行学习,由编码器对问题的输入序列进行编码,再利用解码器结合注意力计算方法,以自回归的方式逐步构造解,根据学习到的特征进行后续的节点预测。进一步地,Ma等人[15]把PN与GNN相结合提出图指针网络(graph pointer network,GPN),利用GNN提取计算节点特征,再用PN进行解的构造,提升了大规模TSP问题的泛化能力。与大多数经典启发式算法相比,基于RL训练的模型对问题变化具有鲁棒性,当问题输入发生变化时,RL可以自动适应问题变化输出较优的解。
最近,受Transformer[16]架构的启发,Kool等人[17]借用Transformer提出新框架,其主要求解思路是利用AM对模型进行改进,提出将输入元素分为静动态两种表示,利用嵌入的方式替代循环神经网络(recurrent neural network,RNN)的编码过程对静动态元素进行向量表示,解码阶段将静态向量表示输入到解码RNN中获得隐含层向量与动态向量结合,通过AM获得下一个决策点的概率分布,超越了先前解决路径问题的优化性能。后续的研究工作大部分是基于Kool等人[17]的AM模型开展的,经过不断调整编码器、解码器的结构以及RL训练方法,进一步提升VRP的优化性能。
本文对近年来利用DRL方法求解VRP进行文献综述,对各种网络模型的结构进行详细分析,并比较各个算法模型的优缺点以及优化性能,指出未来求解路径问题的解决思路,为学者在基于DRL求解VRP方向的研究提供指导。
1 深度强化学习的介绍
本章讨论求解VRP的DRL方法,RL通过智能体与环境交互的方式不断学习,使预期回报最大化。下面介绍RL相关原理和将VRP转化为序列决策问题的马尔可夫决策过程(Markov decision process,MDP)[18],以及经典的RL算法[19]。
1.1 强化学习
RL是智能体在与环境的交互过程中,通过学习策略以最大化提高奖励或实现特定目标的模型。RL可以建模为MDP,MDP实际就是一个多元组[S,A,P,R,γ]。其中,初始状态空间S(st∈S)是起点城市或是部分解;A为动作空间(at∈A),动作是对部分解的添加或者对完整解进行改变;P为状态转移概率矩阵;R是奖励函数,表明在特定状态下选择的动作对解决方案造成的影响。γ∈(0,1)是折扣因子,调控智能体考虑短期回报。
RL详细操作如图2,智能体执行动作at之后,环境会转换到新状态st+1,并给出奖励信号rt+1,智能体根据新状态st+1以及奖励信号rt+1按照训练的策略π执行新动作at+1。以TSP问题为例,初始环境st为已访问的城市或起始城市节点,新状态st+1是实时更新的解决方案,动作at是下一个将要访问的城市,奖励信号rt在访问完节点时(以负的路径长度)激励智能体做出下一步决策。

图2 强化学习简要模型Fig.2 Brief model of reinforcement learning
1.2 强化学习算法
RL算法[19]主要分为两大类,有模型学习和无模型学习。有模型学习对环境有提前的认知,可以提前感知优化;无模型学习在训练速度上逊于前者,但更易实现,在真实场景下可以快速调整到较优的状态。利用RL解决VRP的方法主要分为:基于值函数的方法和基于策略优化的方法。RL算法详细分类如图3。

图3 机器学习算法分类Fig.3 Machine learning algorithm classification
2 DRL求解车辆路径问题的思路
2.1 车辆路径问题的简单概述
随着电商在线销量的增加,物流产业的快速发展,VRP问题一直是COP的研究热点。如何提高解的精度,加快搜索速度,减少时间复杂度、增强模型泛化能力等是求解VRP最关注的问题。在实际场景中,VRP会超出普通路径问题的限制,例如,带有时间窗口的旅行商问题(traveling salesman problem with time windows,TSPTW)[20]将时间窗口约束添加到TSP中的节点,即节点只能在固定的时间间隔内访问;带容量的车辆路径问题(capacity vehicle routing problem,CVRP)[21],旨在为访问一组客户(即城市)的车队(即多个销售人员)找到最佳路线,每辆车都具有最大承载容量的限制。VRP根据不同的应用场景和现实条件需要考虑更多的约束(车载容量、配送中心数量、车辆行驶里程、时间限制等),因此衍生出许多变体,例如:带时间窗的车辆路径问题(vehicle routing problem with time windows,VRPTW)[22]、无人机和卡车协同配送的无人机车辆路径问题(vehicle routing problem with drones,VRPD)[23]、多车型车辆路径问题(heterogeneous fleet vehicle routing problem,HFVRP)[24]等。
2.2 基于深度强化学习求解路径问题的步骤
利用DRL求解VRP的思路是将城市的原始坐标作为输入,利用PN,GNN或Transformer结合经典图搜索算法建设性地构建近似解,整体求解框架见图4。

图4 求解整体框架Fig.4 Solving overall framework
步骤1将问题转化为图结构信息,VRP问题是一个全连接图,图的节点对应于城市节点,边对应两城市之间的道路,如图5所示。图通过启发式算法进行稀疏化,使模型能够扩展到所有节点的成对计算来解决难以处理的大型实例,或者通过减少搜索空间来更快地学习策略。

图5 问题定义Fig.5 Problem definition
步骤2获取图中节点和边的初始嵌入,如图6所示。嵌入是GNN或Transformer编码器将TSP图中的每个节点或边作为输入,来计算高维空间表示或嵌入特征。在编码的每一层,节点从其邻居节点收集特征,通过递归传递表示局部图结构。堆叠L层后,网络能够从每个节点的L层邻域中构建节点的特征。Transformer中基于AM的GNN已成为编码路径问题的默认选择,AM作用在于根据对现在节点的相对重要性来权衡邻居节点。

图6 图嵌入Fig.6 Graph embedding
步骤3图的节点或边被编码为高维空间表示,解码为离散的TSP,如图7所示。首先,将概率分配给每个节点或每条边,通过分配的概率将节点或边添加到解集中;然后通过经典图搜索技术(例如由概率预测引导的贪心搜索或波束搜索)将预测概率转换为离散决策。

图7 解码和搜索Fig.7 Decoding and searching
步骤4模型训练。整个编码器-解码器模型以端到端的方式进行训练,一般情况下,通过模仿最优求解器来训练模型以产生接近最优的解。
由于TSP问题通常需要顺序决策以最小化特定于问题的成本函数,可以天然地利用RL框架训练智能体最大化奖励函数。对于未充分研究的问题以及缺乏标准解决方案的情况下,RL是一种最优的替代方案。
3 基于DRL求解VRP的方法
近年来出现的大量研究,旨在使用DRL方法开发新的学习算法来自动解决路径问题,以实现动态高效的求解。DRL求解VRP的方法主要分为PN、GNN、Transformer以及混合模型四类模型。以上通用的路径问题求解框架,可以适用于求解VRP的变体问题,运行速度和精度相比传统算法有较大优势。表1和表2对近几年求解TSP及其变体问题和VRP及其变体问题的模型进行分析与总结。下面对以上四类模型方法进行介绍,对各类方法的代表性模型、优化性能进行对比和分析。
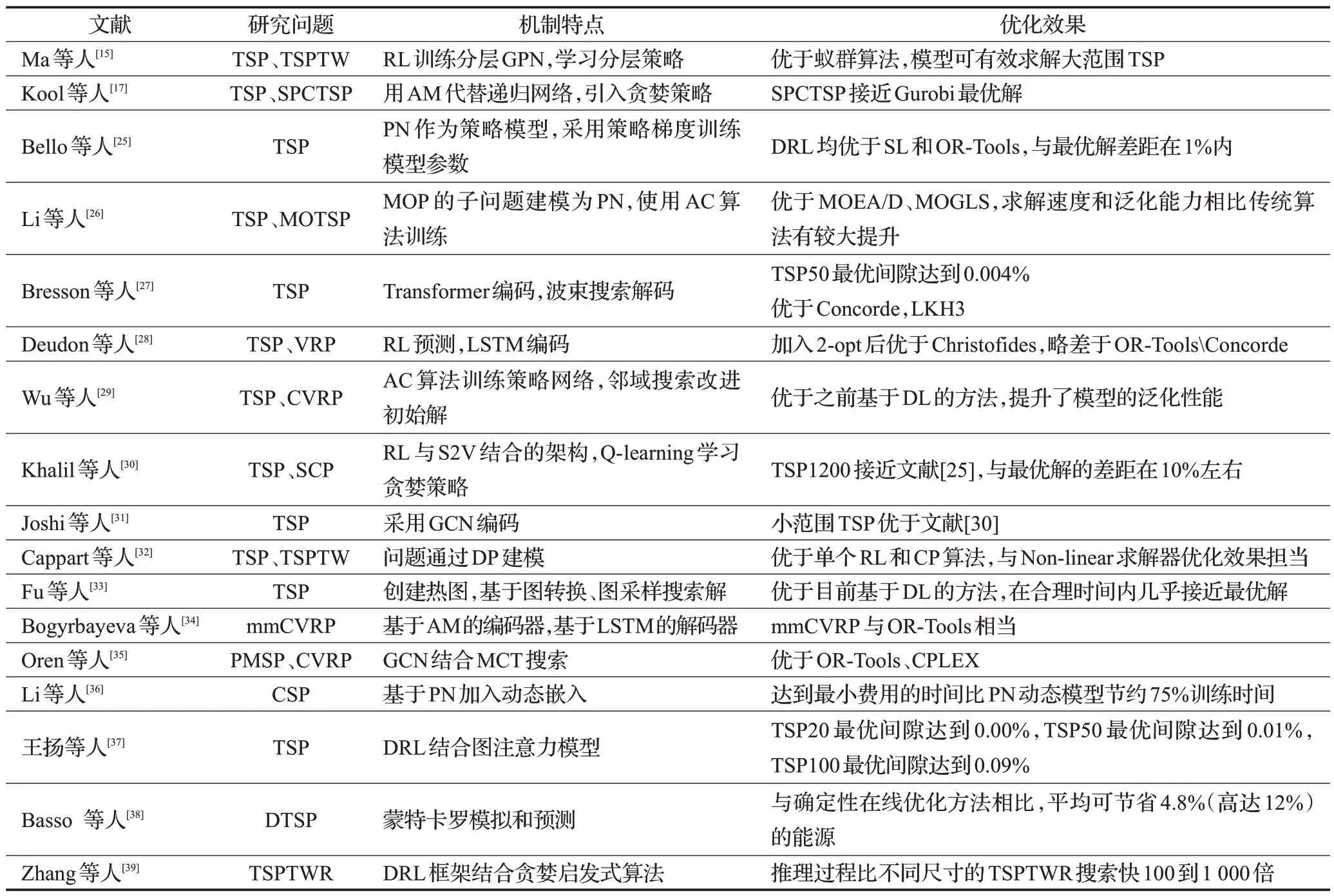
表1 TSP及其变体问题的模型算法分析与总结Table 1 Model algorithm analysis and summary of TSP and its variant problems

表2 VRP及其变体问题的模型算法分析与总结Table 2 Model algorithm analysis and summary of VRP and its variant problems
3.1 基于PN求解VRP
3.1.1 求解模型
2015年Vinyals等人[12]首次提出将PN与VRP结合,使得模型架构不受输入输出维度的限制,采用SL方式进行离线训练,以预测访问城市的序列,解决了小规模的TSP问题,为PN求解VRP开辟了新的道路。PN模型原理是将VRP问题编码成向量,使其在隐层输出、解码时通过激活函数对向量进行处理,输出问题实例中较大的概率向量。例如PN求解TSP的步骤为:首先将每个城市的坐标转化为高维节点特征向量,由编码器读入城市坐标,编码为对应的存储输入序列信息的向量,然后解码器对向量进行解码,在解码过程中,利用AM和隐层状态计算选择各个城市的概率P(yt|y1,y2,…,yt-1),在解码时使用uit作为指向向量选择输入序列中的元素。
Vinyals等人[12]以SL方式训练模型,需要大量TSP示例及其最优解作为训练集,标签不易获得。为了摆脱对高质量标签的依赖,Bello等人[25]采用了RL中的行动者-评论家(actor-critic,AC)算法训练网络参数,提出神经组合优化(neural combinatorial optimization,NCO)模型,以PN为基础构建策略网络,训练过程中模型输出的序列值可以通过深度神经网络(deep neural network,DNN)训练估值网络参数,再通过奖励机制微调,不断改进策略网络,扩大了TSP的求解规模,但该框架不适用于随时间变化的更复杂的VRP问题。在此基础上,Nazari等人[40]提出了一种可以系统处理静态和动态元素的训练方法,模型对输入序列保持不变,因此改变任何两个输入的顺序不会影响模型状态。在VRP问题中输入是无序的客户位置及客户需求,输入顺序对问题求解影响较小,因此模型未采用RNN编码器,而通过简单的节点嵌入替换了PN的LSTM编码器,进而缩短了训练时间,且不会降低模型的训练效率。
面对多目标优化问题(multi-objective optimization problems,MOPs)时,Li等人[26]提出了一种使用DRL解决MOP的端到端框架,模型将多目标问题分解为一系列子问题,再通过PN来解决多目标旅行商问题(multiobjective traveling salesman problem,MOTSP)。该模型探索了使用DRL以端到端的方式求解MOTSP的可能性,即给定n个城市作为输入,可以通过训练网络的前向传播直接获得最优解。
3.1.2 模型总结
以上模型依赖梯度信息指导搜索,基于搜索的求解VRP方法通常由启发式方法指导,在各种条件和情况下调整启发式方法通常非常耗时。为此Chen等人[41]使用双向LSTM嵌入路径,提出NeuRewriter模型,模型学习一种策略来选择启发式方法并重写当前解决方案的局部组件,以迭代方式改进直到收敛。实验果表明模型可求出CVRP20的最优解,CVRP100的优化性能优于求解器OR-Tools。
3.2 基于Transformer求解VRP
3.2.1 求解模型
RNN参数在序列的所有元素之间共享,当模型获取最后一个时间步的输出时,它可能会“忘记”序列中先前元素的信息。而AM通过保留编码器对输入序列的隐层向量序列,在解码阶段对获得的向量序列加权求和得到上下文向量ct,由于在输出过程中注意力的权重不同,因此权重参数αit越大,在t时刻输出第i个向量的概率越大。进一步,Google团队[16]提出了由AM和多层感知机组成的网络结构“Transformer”,Transformer的MHA可以注意到子空间的信息,从不同角度、不同维度提取到问题的深层特征,允许节点通过不同的通道传递相关信息,实现并行计算。因此来自编码的节点嵌入可以学习图的上下文中关于节点的信息。
Kool等人[17]提出了一种有效的模型和训练方法,以改进上述基于学习的启发式求解路径问题。通过用AM层代替递归网络来减少节点输入顺序的影响,应用RL算法训练模型。与Bello等人[25]不同,此模型引入贪婪策略得到的解作为基线,提高了模型的收敛速度。Joshi等人[31]基于Kool等人[17]的实验设置,结合SL和RL训练100个节点的TSP,提升了模型的准确率。
在Kool等人[17]模型中,节点特征通过嵌入方式进行编码,该嵌入随时间推移而固定。而问题实例的状态应根据模型在不同的构造步骤所做的决定而改变,节点特征应该相应地更新。因此,Peng等人[48]提出了一种具有动态编码器-解码器结构的动态注意力模型,该模型能够动态地探索节点特征,并在不同的构造步骤中有效地利用隐藏的结构信息。与Kool等人[17]相比,该模型在图的上下文中动态地刻画每个节点,这可以在不同的构造步骤中有效地探索和利用隐藏的结构信息。
受Transformer在NLP中的启发,Bresson等人[27]将Transformer用于求解TSP,编码器与Kool等人[17]和Deudon等人[28]相同,通过RL训练模型,使用带有MHA模块的部分解来构建查询,添加一个不存在的城市,该城市通过自注意力模块查询所有城市,并在最佳位置使用波束搜索解码。结果表明,TSP50的最优间隙为0.004%,TSP100的最优间隙为0.39%。
虽然DRL方法可以直接输出问题的解,但是其优化效果与专业求解器相比仍有一定差距。由于局部搜索是求解组合优化问题的经典方法,学者们开始研究利用DRL方法来自动学习局部搜索算法的启发式规则,从而比人工设计的搜索规则具有更好的搜索能力。相比之下,Wu等人[29]利用DRL来自动发现更好的改进策略,提出了一个DRL框架来改进启发式算法解决路径问题。模型首先提出一种用于改进启发式算法的RL公式,其中策略网络由两部分组成,分别学习节点嵌入和节点对选择,用来指导下一个解决方案的选择;并利用AC算法训练策略网络,然后通过邻域搜索来改进初始解,不断地提高解的质量,最后利用基于自注意力的框架参数化策略。将模型应用于求解TSP和CVRP的实验结果表明,模型明显优于现有的基于线性规划的求解TSP和CVRP方法,在改进启发式算法过程中,学习到的策略确实比传统的手工规则更有效,并且可以通过简单的集成策略进一步增强。
基于Transformer还有更多的改进,Falkner等人[49]采用修复和破坏算子,通过局部搜索过程和维护少量候选解来进一步扩展大邻域搜索(large neighborhood search,LNS)。LNS是神经修复算子与局部搜索过程、启发式破坏算子和部分解的选择过程相结合,以获得高效的求解方法,LNS主要思想是利用学习的模型来重构部分被破坏的解,并通过破坏启发式(或随机策略本身)引入随机性来有效地探索大邻域。文献[49]启发式方法针对解决方案的不同部分,将销毁分为两种不同的操作:创建部分路线、删除完整的路线。与文献[49]每次考虑一个节点的构造启发式相反,Hottung和Tierney[50]直接学习神经修复算子,以重新组合由CVRP的随机分裂产生的路径片段。
基于Falkner等人[49],Ma等人[51]提出双方面协作Transformer(dual-aspect collaborative transformer,DACT)神经领域搜索模型,使用双向编码器分别学习节点和位置特征的嵌入,利用循环格雷码邻接相似、首尾相似的特性设计高维空间连续的循环位置编码(cyclic positional encoding,CPE),训练过程中使用课程学习获得更高效的采样速率,以及更快的收敛速度和更小的方差,提高求解VRP的泛化性能。应用DACT求解TSP和CVRP的结果表明,DACT优于现有的邻域搜索求解器,并且具有更优的泛化性能。
3.2.2 模型总结
现实生活中VRP问题涉及车辆容量、时间窗口等约束,虽然近年来已经开发了RL模型来比优化启发式更快地解决基本的VRP问题,但很少考虑复杂的约束。启发式算法高效的邻域搜索功能是求解VRP问题的关键组成部分,Ma等人[52]针对取货和送货问题(pickup and delivery problem,PDP)问题设计基于并改进DACT[51]的神经邻域搜索方法N2S,N2S将DACT-Attention改进为高效的Synth-Attention,允许最基本的自我注意机制合成关于解决方案的各种特征,同时利用两个自定义解码器自动学习执行取货和送货节点对的移除和重新插入,以解决优先级约束。模型甚至在更多约束的PDP变体上超过了人工设计的LKH3求解器。
3.3 基于GNN模型求解VRP
3.3.1 求解模型
近年来,研究人员设计了用于处理图数据的神经网络结构GNN,其核心思想是根据每个节点的原始信息(如城市坐标)和各个节点之间的关系(城市之间的距离),计算得到各个节点的特征向量,依据节点特征向量进行节点预测、边预测等任务。GNN与图嵌入密切相关,图嵌入旨在通过保留图的拓扑结构和节点内容信息,将图中顶点表示为低维向量,以便使用RL算法进行处理。Scarselli等人[14]利用GNN模型处理图上的数据表示问题,实现了函数将图中的节点映射到多维欧几里德空间,适用于以图及其节点为中心的应用。
GNN通过低维的向量信息来表征图的节点及拓扑结构,有效的提取图中关键节点信息。Nowak等人[53]以SL的方式训练GNN,直接输出一个环游作为邻接矩阵,结合波束搜索将其转换为可行的路径方案。该方法被提出之后,structure2vec(S2V)[54]、GCN[54]、图注意力网络(graph attention network,GAT)[54]等模型相继被提出,用于解决VRP。
在许多实例中,相似的路径问题通常保持相似的问题结构,但数据不同,这为学习启发式算法提供了契机。Khalil等人[30]指出上述网络架构不能有效反映TSP的图结构,并提出了一种将RL与图嵌入神经网络相结合的框架,以增量方式构造TSP和其他VRP问题的解决方案,引入基于S2V的图嵌入网络,以捕获解决方案的当前状态和图的结构,然后使用Q-learning来学习贪婪策略,该策略决定将哪个顶点插入部分游览,可求解大范围的TSP问题。
GPN扩展了传统的PN,增加了一层图嵌入,这种转换实现了对大规模问题的更好推广。Kool等人[17]将GNN和PN进行结合求解CVRP,加入MHA以及自注意力机制,AM能有效地捕捉深层节点信息,采用AM计算每一步的节点选择概率,以自回归的方式逐步构造得到完整解,且模型通过设计超参数展示了在合理大小的多个VRP问题上的灵活性。为学习更好的启发式方法解决广泛的VRP问题提供思路。
Joshi等人[31]基于Kool等人[17]的实验设置,在PN基础上用图卷积神经网络(graph convolutional networks,GCN)编码代替Transformer架构编码,结合SL和RL训练100个节点的TSP,提升了模型的准确率,利用SL训练GNN,以预测边出现在TSP中的概率,通过波束搜索生成可行的回路。为TSP20/50/100训练基于自回归的GAT模型,并评估从TSP20到TSP500的实例,通过REINFORCE训练RL模型和贪婪算法推出基线,以最大限度地减少模型在每一步的预测和最优目标。
GCN[54]是许多复杂GNN模型的基础,其核心思想是学习一个函数映射,通过映射图中的节点,聚合节点与其邻居节点的特征来生成节点的新表示。Groshev等人[55]和Joshi等人[56]通过SL训练GCN来解决TSP。Joshi等人[56]在TSP20/50/100的优化效果略微超越了Kool等人[17]的方法,接近LKH3、Concorde等求解器得到的最优解,但是该方法的求解时间慢于LKH3、Concorde等方法,在泛化能力上该方法也不及Kool等人[17]的方法。Groshev等人[55]使用经过训练的GCN来指导启发式算法输出解决方案,利用这些解决方案作为标签重新训练大规模TSP的GCN,进一步,Prates等人[57]使用SL来训练GNN,将边缘权重视为每个实例的特征,模型输出的解决方案与最优解的偏差可以小于2%。
以上工作都是利用人工智能的泛化能力来探索满足问题的车辆路径,仍受到城市规模、大型交通网络带来的计算复杂度的困扰。James等人[58]提出一种基于DRL的NCO策略,将在线VRP问题转换为车辆游览生成问题,并提出一种图嵌入式PN结构来迭代开发游览。由于构造NN所需的SL数据具有高计算复杂度,利用具有无监督辅助网络的DRL机制来训练模型参数,同时设计多采样方案,以进一步提高模型性能。
3.3.2 模型总结
GNN和GCN用来提取图的特征并部署记忆增强NN和RNN传递顺序信息,GAT是一种基于空间的GCN网络。GAT是通过AM传播节点信息,对图拓扑具有强大的表示能力。因此,Gao等人[42]在GAT基础上改进提出EGATE模型(element-wise GAT with edgeembedding,EGATE),模型的编码器是将节点嵌入和边嵌入集成修改的GAT,以及一个基于GRU的解码器,模型通过AC训练,实验结果表明,在中等规模的数据集上,该模型优于传统启发式算法和NCO模型,能够处理大规模数据集。由于VRP问题的高复杂性,难以扩展且大多受到问题模型容量的限制。因此,学者提出利用混合方法来求解VRP及其变体问题。
3.4 混合模型求解VRP
3.4.1 RL结合传统算法求解VRP
在求解CVRP问题时,LKH3等经典算法求解效率低,难以扩展到更大的问题。基于DRL的方法求解效率高,但是DRL解的质量与传统经典方法求得解的质量仍存在相当大的差距,为此Lu等人[59]提出一种在解决方案中迭代搜索,通过不断地改善解,直到满足某个终止条件的框架。模型将启发式算子分为改进算子和扰动算子,即给定一个问题实例,算法首先生成一个可行解,然后用改进算子或扰动算子迭代地更新解,在一定次数的步骤之后,模型将在所有访问的解决方案中选择最好的一个。
经典算法除了求解效率不高,求解VRP问题还面临着状态空间爆炸问题,可行解的数量随着问题规模的大小呈指数级增长,使得解决大规模VRP变得棘手。Cappart等人[32]提出一种基于DRL和约束规划(constraint programming,CP)混合模型求解TSPTW,模型核心是将TSPTW通过动态规划(dynamic programing,DP)建模,模型架构分为三个部分:学习阶段、求解阶段和统一表示,其中智能体的动作衔接学习和求解两个阶段,学习阶段是通过RL训练问题实例,求解阶段利用CP评估问题实例。通过实验证明,该模型的性能优于独立的RL和CP解决方案,与求解器OR-Tools效果担当。
为进一步提高模型的泛化能力,Fu等人[33]提出一个在固定大小的图上预训练的网络,通过对子图进行采样,推断和合并结果以解决更大规模的问题。在此基础上,Xin等人[60]提出将DL与传统启发式LKH相结合的算法NeuroLKH解决TSP。该模型训练了一个稀疏图网络(sparse graph network,SGN),分别通过SL和无监督学习训练边缘分数、节点惩罚,以此提高LKH的性能,基于SGN的输出,NeuroLKH创建边缘候选集并转换边缘距离以指导LKH的搜索过程。文献[60]实验结果显示,NeuroLKH显著优于LKH,并且模型可以很好地推广到CVRP、PDP。
DRL方法通常缺少在解空间内搜索的能力。为克服以上问题,王原等人[61]提出了深度智慧型蚁群优化算法(deep intelligent ant colony optimization,DIACO),采用DRL方法提取问题特征,并形成对应的特征矩阵,蚁群算法基于特征矩阵进行搜索求解,蚁群算法的加入提高了DRL解空间搜索性能,同时DRL提升了蚁群算法的计算能力,该方法能够有效求解不同规模的TSP。
一些求解VRP的模型可以通过Q-learning很好地训练,但不能通过Sarsa训练,降低了模型的性能。因此,Zheng等人[62]提出一种基于RL的启发式算法VSR-LKH,该算法显著提升了著名的LKH算法,它将Q-learning、Sarsa和MCT三种算法相结合,取代LKH的遍历操作,是一种可变策略。可变策略的思想是受可变邻域搜索的启发,定义一个Q值来代替α值,通过结合城市距离和α值来进行候选城市的选择和排序,并且通过迭代搜索过程中产生的可行解的信息自适应地调整Q值,以进一步提高模型泛化性能。
3.4.2 RL与神经网络相结合的混合模型
由于RL学习方法大多直接学习端到端的解决方案,以及VRP问题的高复杂性,难以扩展且受到RL模型容量的限制,为克服上述问题,Wang等人[63]设计了一个双层框架求解器,上层学习框架来优化图(例如,添加、删除或修改图中的边),下层启发式算法在优化的图上求解,这样的双层网络简化了对原始问题的学习,并且可以有效地减轻对模型容量的需求。
面对更复杂或者大范围的路径问题时,经典的DRL算法仍然得不到好的优化效果,训练好的模型泛化到大范围时解的质量会下降。于是研究者提出了分层强化学习(hierarchical reinforcement learning,HRL)模型,HRL在面对高维度问题时不会出现维度灾难,将一个复杂的问题分解为简单的子问题,从而来解决大规模的TSP。Ma等人[15]使用RL训练分层GPN,在约束条件下学习分层策略寻找最优解,该模型在小范围TSP训练且泛化到大范围TSP也具有更快的计算速度和最短距离。
而对于问题TSP-D,Bogyrbayeva等人[34]提出了一种AM-LSTM混合模型,用于考虑车辆和无人机之间交互作用的高效路径,该模型由一个基于AM的编码器和一个基于LSTM的解码器组成,AM对高度连通的图形进行编码,LSTM存储所有车辆的历史路径。数值结果所示,这种混合模型在解决方案质量和计算效率方面都优于基于AM机制的模型,以及模型泛化到对最小-最大容量约束车辆路径问题的实验也证实了混合模型比基于注意的模型更适合于多车辆协调的路径问题。
与启发式方法相比,经典的DP算法保证了最优解,但随着问题规模的增大使得泛化性很差。为此Kool等人[64]提出深度策略动态规划(deep policy dynamic programming,DPDP),将神经启发式的优势与DP算法的优势相结合。DPDP使用来自DNN的策略对DP状态空间进行优先级排序和限制,以及使用GNN对部分解进行评估,对DP算法进行“神经增强”。实验结果表明,神经策略有效地提高了DP算法的性能,对于具有TSP100,该方法产生与高度优化的LKH求解器相接近的结果,在TSPTW100上,DPDP的求解速度显著快于LKH。
面对CVRP,王扬等人[43]提出动态图Transformer(dynamic graph transformer model,DGTM)混合模型,使用动态位置编码技术,用于循环编码动态序列,使得节点坐标在嵌入过程满足平移不变性,其次将GNN的聚合操作处理应用于Transformer解码架构中,最后通过双重损失的REINFORECE算法训练DGTM,有效调节不同节点间的差异分布程度,防止过早收敛。DGTM在处理CVRP问题上优化结果得到显著提高且具有较好的泛化性能。
3.4.3 模型总结
之前关于求解车辆路径的工作主要集中在自回归模型,但当与任何形式的搜索方法相结合时,需要为每个部分解来评估模型,导致模型的计算成本很高。而Kool等人[64]提出的模型每个实例只需要对NN进行一次评估,因此可以进行更大范围的搜索。
4 DRL求解VRP的分析
4.1 求解方法局限性
利用RL求解VRP需要不断调整参数,改进策略网络,在训练过程中难免会出现模型不稳定、泛化能力差或过于依赖标签等情况,都会对模型的最终性能造成影响。下面分别对基于PN、基于GNN、基于Transformer和混合模型求解VRP的相关模型进行局限性分析。
基于PN模型局限性分析:PN结构简单,无法处理动态信息;网络层数少,不利于充分提取问题的特征信息;在处理动态信息过程中,信息本身的不稳定性、节点信息稀疏性都会限制模型的优化效果影响解的输出。
基于Transformer模型局限性分析:网络层数多、结构复杂,模型参数变多且不易训练。
基于GNN模型局限性分析:模型需借助验证集早停提升模型性能;训练是整个批次进行的,难以扩展到大规模网络,且收敛较慢;网络层数太深时,模型参数不能得到有效的训练;图的拓扑性质会导致巨大的解空间在搜索过程也是困难的,从而限制模型的优化效果。
混合模型求解VRP局限性分析:使用传统算法搜索导致训练时间较长,优化性能无法保证,可能出现解码错误等情况。
因此无论是基于图结构模型、还是基于DRL结合传统算法模型求解VRP,都有一定的局限性,表3对求解VRP的经典模型进行局限性分析。

表3 DRL求解VRP的模型局限性分析Table 3 Model limitation analysis for DRL solving VRPs
4.2 RL求解VRP问题的优势及实验对比
VRP有很多变体涉及动态不确定因素,利用传统方法求解问题难度很大,且不会有很大的突破[68]。RL与传统算法的结合求得的结果优于只使用传统算法的结果,例如Alipour等人[69]面对多约束条件的路径问题,使用RL算法使问题描述更加全面,解的质量也很高。VRP变体都是在经典的TSP上衍生的,具有相似的优化结构,传统算法在问题描述发生轻微变化时,就要重新设计算法,面对VRP众多变体,设计很多算法将消耗大量人力,因此,单独地使用传统算法是不可行的。
在面对具有多个约束条件的问题时,输入输出是随机的、动态的,且前一步的结果可能会对下一步求解有影响。一些传统算法难以考虑随机和动态因素,导致模型泛化能力弱,不能在各个变体中通用或者得到解的质量很差。而NN中的嵌入方式可以根据问题的情况做静态嵌入和动态嵌入,充分保证了原始问题的真实性。Li等人[36]提出DRL方法求解覆盖旅行商问题(covering salesman problem,CSP),模型基于PN加入动态嵌入模型处理动态信息,计算速度比传统启发式快近20倍。利用RL求解VRP与传统方法相比,RL有优质的表现和泛化能力,加入动态嵌入可以更好地处理动态信息,深层次的网络更有利于提取深层次潜在的隐含信息。
总的来说,RL求解VRP相比传统算法的优势如下:(1)求解速度快。DNN模型对问题特征进行全方位的表示,减少了解空间的搜索宽度和深度;硬件设施CPU更高、更快、更强和GPU在ML领域的优异表现,使得VRP问题在最短的计算时间内得到显著的优化效果;模型一旦训练完成,以O(n)的复杂度输出解。(2)泛化能力的提高。面对具有相似结构的问题,只需调用参数通过迁移学习传递给相应的策略函数,就能输出合适的解,减少对数据标签的依赖性,节省大量资源和计算时间。通过DRL学出来的策略有希望比人工设计出来的更高效,不需要重新设计算法。(3)解决了多维度问题。面对多维度问题,可以使用不同嵌入方式结合AM使问题的描述更加详细,挖掘更深层次的关系,从而输出高质量的解。DRL有望能够求解一些复杂约束条件下的NP难问题。
本文对端到端的DRL方法作了详细的介绍,为保持实验数据公平性,所有实验均基于Pytorch-1.9.0深度学习平台,在Windows11操作系统环境下使用单张Nvidia RTX 3050 GPU和i5-11300H CPU运行VRP模型,这里总结了常用的基于DRL的方法和启发式算法的最新实验结果,表4是针对CVRPlib数据集实例上具有代表性模型的优化效果的对比。实验结果显示,DACT模型的优化性能超越了目前基于DRL的模型和专业求解器。

表4 经典模型在CVRPlib数据集实例上的性能比较Table 4 Performance comparison of solutions for CVRPlib on instances
5 总结及未来发展方向
最近,许多研究人员回顾了基于RL求解VRP,每篇综述都有各自的优点和不足,本文对最近发表的综述进行整理分析:Mazyavkina等人[70]总结了一些常用的基于策略和基于价值的强化学习算法,没有比较模型间的差距,没有数据对比;Kotary等人[71]对ML学习方法进行分类,侧重于端到端的学习范式,笼统地介绍了GNN;Cappart等人[72]对GNN在各种推理任务中的应用进行了高级概述没有描述学习在CO推理中的具体作用和过程;Bengio等人[73]对COP的ML算法进行概述,为ML应用到COP提供理论基础,但未对ML求解COP的建模过程进行详细介绍。
DRL将VRP问题与DNN结合起来,将VRP的特殊性和DRL的优势结合起来,克服了单独使用传统算法求解效果不理想的局限性,是目前解决VRP及其变体最流行的方法。本文对RL的相关算法以及DRL模型的构建过程进行了详细的介绍,并梳理了先前模型的创新点和不足之处,重点分析了DRL模型架构的主要作用和特性。VRP是多变体多维度的,且现实数据与训练数据会有差距,导致模型在应用到实例会出现效果不好、最优间隙差等情况,由这些模型的不足可以看到,将来使用DRL解决VRP及其变体问题仍存在挑战性。
(1)现有基于学习的方法仅仅训练特定的路径问题,对特定路径问题的范围进行泛化求解。未来可以考虑将训练完成的路径策略通过迁移学习技术,在不同实例上进行泛化求解,会节省大量的计算资源,提高模型的利用率。进一步深入探求不同参数之间的内在联系,建立VRP问题变体之间的源域到目标域的映射关系是未来值得研究的问题。
(2)现有RL模型求解VRP属于端到端的方法,求解过程类似于黑箱优化,缺乏相应的理论保证。未来工作中,寻找一种通用的体系结构,有效地保证DRL求解方法的可行性,还需要进一步评估和检验。未来工作中可以考虑将DRL及其网络架构迁移至运筹优化算法中,以增强求解的可靠性。因此继续深入探求DRL的求解过程和增强模型的可解释性是未来值得研究的问题。
(3)大多数网络使用均匀分布或者随机生成数据来训练策略网络,训练好的模型可以泛化到不同的问题上,但是模型泛化能力的好坏或许与训练数据有关,若节点位置分布不知或不遵循任何分布,此时构建一个稳定的模型具有很大挑战。如何为VRP及其变体问题构建鲁棒性的训练模型是未来工作中的关键研究点。未来考虑通过知识蒸馏的方法提升DRL模型在不同数据分布下的泛化能力。
(4)RL含有大量手工设计的超参数,不同的参数往往对模型的性能影响较大。为减少超参数对实验结果的影响,考虑将自动RL参数调整技术引入到模型训练中。自动调整学习率和衰减率对模型收敛性的控制是未来一个重要的研究方向。

