基于图像直观的导数题的解题与命题尝试
刘海涛
(1.安徽省芜湖市第一中学 2.新青年数学教师工作室)
纵观近年来的高考题及各级各类模拟题,导数题大多作为压轴题出现,且常考常新,使得学生对导数题望而生畏、望而却步,甚至被动放弃.笔者梳理高考卷和模拟卷中的导数题,发现对于大多数的导数题,若能借助图像直观分析题意,则可快速锁定解题思路,顺利解题.笔者首先基于图像直观视角给出一道模考题(母题)的分析与解答,再借助母题中的函数图像,尝试不同的构造,为读者展示四种常见导数题型的命制与解答.
1 母题的呈现与分析
母题已知f(x)=xlnx,g(x)=k(x-1).
(1)求f(x)的极值;
(2)若f(x)≥g(x)在[1,+∞)上恒成立,求实数k的取值范围.

(2)问题可转化为在区间[1,+∞)上,直线y=k(x-1)不在函数f(x)图像的上方,注意到两函数图像均过定点A(1,0),如图1所示,实数k的临界值为函数f(x)在点A处的切线斜率.

图1
设h(x)=xlnx-k(x-1)(x≥1),求导得
h′(x)=lnx+1-k.
当k≤1时,h′(x)=lnx+1-k≥0,h(x)在[1,+∞)上单调递增,有h(x)≥h(1)=0,符合题意.
当k>1时,由h′(x)=0,得x=ek-1,知h(x)在(1,ek-1)上单调递减,则h(x)<h(1)=0,不合题意.
综上,k≤1.
2 图像视角下的试题命制与分析
2.1 端点取等号的不等式问题
有一类不等式恒成立问题,其临界情况(取等号)为区间端点,我们一般称这类不等式为端点取等号的不等式.在2022年新高考Ⅱ卷,2020年全国Ⅰ卷(理科),2019年全国Ⅰ卷(文科)等试卷中均有考查.
如图2-甲所示,构造函数,注意到当时,且f(x)≥h(x)在上恒成立.对于不等式f(x)≥,规定区间为,注意到为不等式的取等条件(此时无法求a的值).构造函数,假设φ(x)≥0恒成立,利用几何画板探究得其恒成立的条件,如图2-乙所示.基于此,命制如下变式题.

图2
变式1已知函数f(x)=xlnx.
(1)求f(x)的单调区间;

2.2 内点取等号的不等式问题
相对于端点取等号的不等式,有一类不等式的临界情况(取等号)为非区间端点(区间内部),我们一般称这类不等式为内点取等号的不等式.其在2020年新高考Ⅰ卷,2018年全国Ⅰ卷(文科)等试卷中均有考查.
如图3-甲所示,构造函数h(x)=aeex-e2x-,使得f(x)≤h(x)在(0,+∞)上恒成立.如何求参数a的范围呢? 关键在于找到取等点(记作x0).

图3
这里,我们可以通过找两曲线公切点的方法来完成,即通过方程组解得x0和a的临界值,从而找到问题的突破口.利用几何画板探究得其恒成立的条件(a≥1),如图3-乙所示.基于此,命制如下变式题.
变式2已知函数f(x)=xlnx.
(1)求f(x)在点(e,f(e))处的切线方程;

当a≥1时,有,欲证f(x)≤h(x),需证,即证.设lnx,求导得,由φ′(x)=0,得,易得φ(x)在上单调递减,在+∞)上单调递增,则得证.
综上,a≥1.
2.3 双变量不等式问题
含有两个变量的不等式问题近年来已成为高考和各级各类模拟考的热点题型,且常考常新,在2021年新高考Ⅰ卷,2016年全国Ⅰ卷(理科)等试卷中均有考查.这类问题主要考查形式有两种:极值点偏移和拐点偏移.
1)极值点偏移问题
当函数f(x)在区间(a,b)内有唯一极值点,且满足f(a)=f(b)时,若a+b=2x0,则称函数f(x)在区间(a,b)内极值点不偏移,常见的不偏移函数有一元二次函数、正弦函数、余弦函数等.若a+b≠2x0,则称函数f(x)在区间(a,b)内极值点偏移,常见的有等由指数函数、对数函数、幂函数复合而成的函数.图4-甲中a+b>2x0,称函数f(x)在区间(a,b)内极值点向左偏移;图4-乙中a+b<2x0,称函数f(x)在区间(a,b)内极值点向右偏移.极值点偏移的根源在于图像的非轴对称性,由此可以考虑将极值点x0一侧的a(或b)通过x0对称,比较两函数值f(2x0-a)和f(b)(或f(2x0-b)和f(a))的大小关系来完成对问题的证明.由母题知函数f(x)在极值点两侧单调性相反,且该函数为非轴对称函数,得函数f(x)发生极值点偏移现象,有,又注意到函数f(x)图像的最左端为坐标原点O(实质上图像并未过该点),且图像与x轴交于点(1,0),有a+b<1.基于此,命制如下变式题.

图4
变式3已知函数f(x)=xlnx.
(1)求f(x)在点(e,f(e))处的切线与两坐标轴围成的三角形的面积;
(2)若两个不相等的正实数a,b满足f(a)=f(b),求证.

如图5所示,函数f(x)的最低点为与x轴交于点A(1,0),得割线l1:y=-x,在点A处的切线为l2:y=x-1.设f(a)=f(b)=m,则a,b是直线y=m与函数f(x)交点的横坐标,设直线y=m与割线l1、切线l2的交点横坐标分别为a′,b′,解得a′=-m,b′=1+m,易知a<a′<b<b′,所以a+b<a′+b′=1.
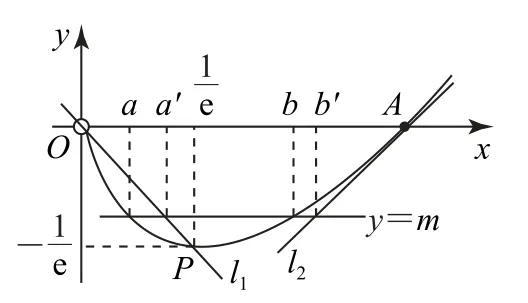
图5
2)拐点偏移问题
当函数f(x)在区间(a,b)内有唯一拐点x0,且满足f(a)+f(b)=2f(x0)时,若a+b=2x0,则称函数f(x)在区间(a,b)内拐点不偏移,常见的不偏移函数有一元三次函数、正弦函数、余弦函数、正切函数等.若a+b≠2x0,则称函数f(x)在区间(a,b)内拐点偏移,如图6-甲所示,a+b>2x0,称函数f(x)在区间(a,b)内拐点向左偏移.

图6
如图6-乙所示,a+b<2x0,称函数f(x)在区间(a,b)内拐点向右偏移.拐点偏移的根源在于图像的非中心对称性,由此可考虑将极值点x0一侧的a(或b)通过x0对称,比较两函数值f(2x0-a)和f(b)(或f(2x0-b)和f(a))的大小关系来完成对问题的证明.如图6-丙所示,构造函数h(x)=2xlnx-x2,注意到其拐点坐标为(1,-1),且属于拐点左移的情况,故当f(a)+f(b)=-2时,有a+b>2.基于此,命制如下变式题.
变式4 已知函数f(x)=xlnx.
(1)求函数g(x)=f(x)-x2+x的最值;
(2)设函数h(x)=2f(x)-x2,若两个不相等的正实数a,b满足h(a)+h(b)=-2,求证:a+b>2.

(2)由题知h(x)=2xlnx-x2,求导得h′(x)=2(lnx-x+1)=2m(x),h″(x)=2m′(x),由(1)知h′(x)≤0,h″(1)=0,得h(x)在(0,+∞)上单调递减,拐点的坐标为(1,-1).
不妨设0<a<1<b,φ(x)=h(2-x)+h(x)+2(0<x<1),求导得φ′(x)=-h′(2-x)+h′(x)=2(m(x)-m(2-x)),又0<x<2-x<1,且m(x)在(0,1)上单调递增,所以φ′(x)<0,则φ(x)在(0,1)上单调递减.又0<a<1,所以φ(a)>φ(1)=0,即h(2-a)+h(a)+2>0,即h(2-a)>h(b),又2-a>1,且h(x)在(1,+∞)上单调递减,所以2-a<b,即a+b>2.
3 小结
我国著名的数学家华罗庚说过:“数无形时少直觉,形少数时难入微”,数与形有着密不可分的关系.在数学学习和研究中,数形结合就显得格外重要,借助图形可以将复杂、抽象的代数式直观化、简单化,利用代数式将图形关系“翻译”出来,可以实现问题的解析化、概括化.我们借助几何图形的直观化,利用图形分析和命制导数题,正是数形结合思想的实践尝试.
(完)

