电磁执行器工作特性分析及补偿控制
张宇,李波,葛文庆,谭草,闫皓,宋爱娟
(1.山东理工大学 交通与车辆工程学院, 山东 淄博 255049;2.南京理工大学 机械工程学院, 江苏 南京210094)
电磁直驱变速系统是一种由直线执行换挡机构驱动的机械式自动变速器,该系统可以提高车辆传动系统的紧凑性,同时还具备高动态响应速度、高传动效率等优点[1]。现阶段对于电磁直驱变速系统的研究主要集中在直线电机结构与工作原理方面,以增加驱动力和提高响应速度作为核心工作,并未过多考虑驱动装置的温升以及位移过程中磁场不均匀引起的换挡力波动问题。因此,需要对电磁直驱变速系统的驱动装置的工作特性进行分析,探究其在运行过程中换档力变化规律并进行相应的补偿控制策略设计。杜志强[2]对直线驱动装置结构以及工作原理进行了分析,提出了一种高精度直线驱动系统控制策略,实验结果表明该控制策略具备一定的可行性。赵玫等[3]对直线电机动子工作状态下的温升特性进行了分析,建立了涡流场与温度场的数学模型,极大减小了温度规律的研究难度。另外,有很多学者致力于直线驱动装置的散热研究,Laithwaite[4]采取了氮气降温的方式对直线驱动装置进行降温和冷却,张武军[5]则采用一种磁性流体对直驱装置进行降温。不难看出,这些方法虽然可以在一定程度上抑制直驱装置的温度升高,但也具有结构设计受限以及成本昂贵等缺点。
受汽车底盘尺寸和布局影响,电磁直驱变速系统应用于车辆传动系统时需要具备特定的结构设计,采用结构降温方式受限。因此本文对电磁直驱变速系统的驱动装置进行实物建模,通过仿真分析得到其在实际位移过程中的驱动力及温升变化规律,同时根据永磁体的剩磁特性建立其温升模型,设计一种基于位移、温度工作特性的驱动力补偿控制方法。
1 执行器工作特性仿真
1.1 执行器驱动力仿真
电磁直驱变速器采用动圈式直线电机作为换挡执行机构,动子线圈磁场中通电后受到的洛伦兹力会带动结合套进行换挡,结构如图1所示。由于磁场分布的不均匀,动子运动在磁场中的不同位置所受到的洛伦兹力也各不相同,为了更好地分析执行器动子在不同位置下的驱动力性能,需要研究动子工作气隙磁通密度的分布规律。在JMAG电磁仿真软件中建立执行器的三维模型,采用静态分析得到在不同位置下的气隙磁通密度如图2所示。
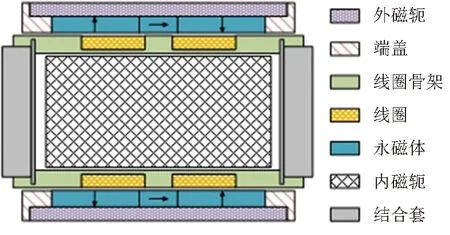
图1 执行器结构
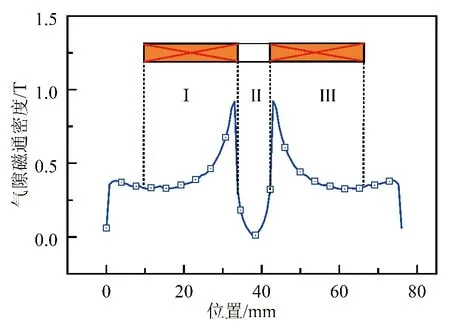
图2 气隙磁通密度分布曲线
从图2可以看出,气隙磁通密度最大值和最小值分别分布在轴向充磁永磁体两侧,这是由于轴向充磁永磁体会增加外侧径向磁力线密度,而其所在区域则相反。当动子线圈运动至区域Ⅱ时,线圈所在的Ⅰ、Ⅲ区域为磁感应强度较大的区域,而线圈换向的分隔骨架处于磁感应强度较小的Ⅱ区域,此时在通电状态下受到的电磁力最大,随着动子的左右移动,线圈进入到磁感应强度较小区域的面积将会越来越大,在通电状态下所受到电磁力也逐渐降低。
在3D模型中添加FEM电路,分别给动子线圈通入10、15、20 A的直流电,运动速度0.072 m/s,位移行程18 mm,得到不同通电条件下,各个位置驱动力变化情况如图3所示。
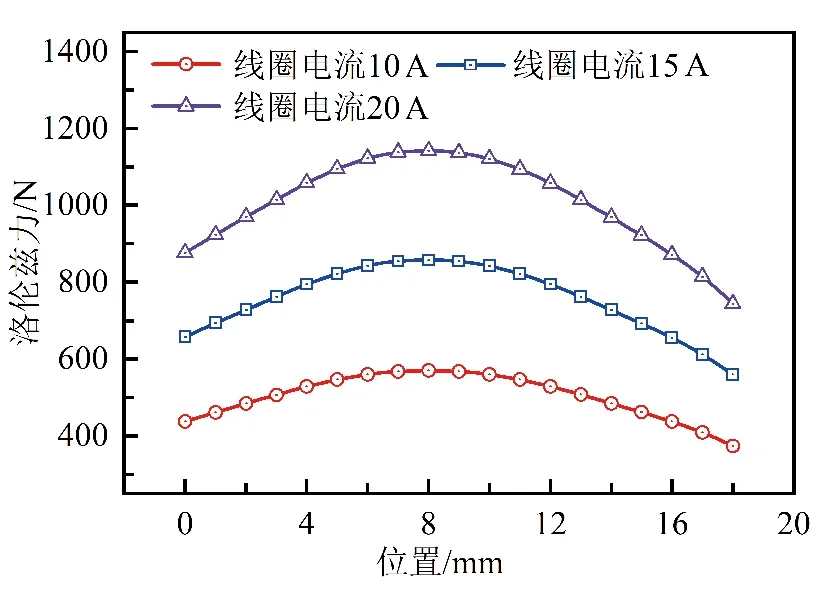
图3 不同输入电流下驱动力变化曲线
由图3可知,在不同的激励电流条件下,动子线圈在直线运动过程中驱动力的变化趋势相同,都呈先增大后减小的趋势,符合气隙磁通密度的分布。在10、15、20 A激励电流所对应的峰值驱动力分别为570、857、1 142 N,对应的最小驱动力为374、560、744 N,驱动力波动较大。
由安培定则可知载流线圈在磁场中受到的电磁力大小为
F=Bli=kei,
(1)
式中:B为气隙磁场强度;l为动子线圈在磁场中的有效长度;ke为电磁力常数,是执行器的特性参数,代表驱动力与电流之间的关系。
由于不同位置下气隙磁场强度的变化,ke也各不相同,将原有的驱动力-位置曲线转化为力常数-位置曲线以消除电流变量。利用Matlab平台Curve Fitting工具对力常数-位置数据点进行拟合,拟合公式为
f(x)=a1*sin(b1x+c1)+a2*sin(b2x+c2)+
a3*sin(b3x+c3)。
(2)
1.2 执行器损耗分析
在JMAG电磁场分析软件中对执行器进行损耗计算,为了使仿真结果与实际换挡更加接近,采用换挡电流曲线作为执行器动子线圈的激励电流,动子线圈电阻值为1.75 Ω,运动速度为0.072 m/s,仿真时长为0.25 s,动子线圈设置铜损条件,内磁轭、外磁轭、永磁体设置铁损条件,得到执行器在一个换挡行程下各部件的损耗情况如图4所示。
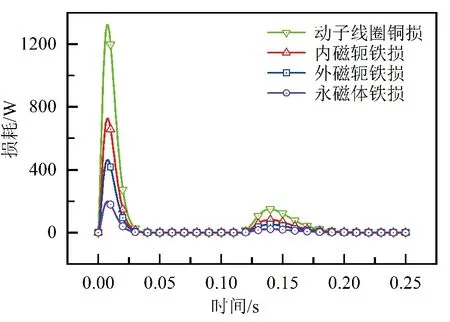
图4 执行器各部件损耗变化曲线
由图4可知,执行器在工作过程中的主要损耗为铜损,其余部件为大块导体材料,其中以内磁轭的体积最大,产生的损耗也最高。损耗主要由通电电流产生,因此损耗集中分布在执行器换挡初期加速阶段与即将完成换挡的减速阶段。
2 执行器等效热路建模
为了准确计算执行器在实际运行过程中永磁体温升引起的剩磁减小问题,需要得到执行器在实际工作过程中的温升变化。由于三维仿真无法实时计算实际工作过程中的温升变化,所以本文采用等效热路法[6]建立执行器电机整体温度场的Matlab仿真模型,结合执行器结构特征,综合考虑执行器内部发热、导热特性,明确热路模型中的等效热源以及各个部分等效热阻和等效热容[7],搭建执行器四热源等效热路图,如图5所示。
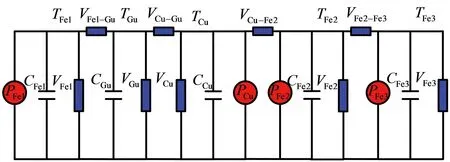
图5 执行器四热源等效热路图
根据图5所设计的执行器四热源等效热路图,结合热路克希荷夫定律[8],采用微分方程形式表示执行器等效热路模型中四个热源产生的热量传递到其他部位的过程,从而得到永磁体在执行器运行过程中的温度变化情况,方程如下:
式中:PFe1为内磁轭铁损;PCu为执行器动子线圈铜损;PFe2为永磁体铁损;PFe3为外磁轭铁损;CFe1为内磁轭热容;CGu为线圈骨架热容;CCu为执行器动子线圈热容;CFe2为永磁体热容;CFe3为外磁轭热容;VFe1为内磁轭热导;VGu为线圈骨架热导;VCu为执行器动子线圈热导;VFe2为永磁体热导;VFe3为外磁轭热导;VFe1-Gu为内磁轭与线圈骨架间的热导;VCu-Gu为线圈骨架与动子线圈间的热导;VCu-Fe2为动子线圈与永磁体间的热导;VFe2-Fe3为永磁体与外磁轭间的热导;TFe1为内磁轭温升;TGu为线圈骨架温升;TCu为执行器动子线圈温升;TFe2为永磁体温升;TFe3为外磁轭温升。
在Matlab/Simulink中搭建执行器四热源的等效热路仿真模型,通过计算并在模型中输入各部件等效热容以及热导,仿真得到执行器连续工作10 min各部分的温度变化结果,如图6所示。
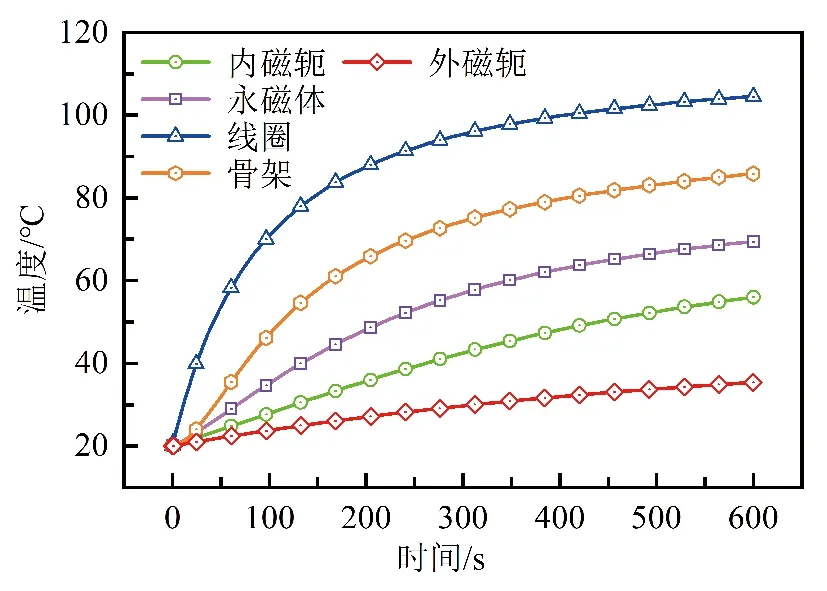
图6 执行器各部件温升曲线
从图6可以看出,动子线圈作为主要热源,在驱动装置中升温最快,与其位置接近的骨架和永磁体温度也较高,而外磁轭和内磁轭距离线圈较远因此温度较低。永磁体的温升变化势必会导致永磁体性能下降[9],从而影响执行器输出力下降,影响执行器性能。
3 执行器工作特性补偿控制
直驱系统驱动电路包括电压源、电阻和线圈电感[10],电气回路数学模型为
(3)
式中:U为电源电压;U(t)为执行器两端电压;R为电阻;L为线圈电感;EM为电磁线圈在磁场中运动产生的反电动势[9]。
对式(3)进行拉普拉斯变换得
(4)
执行器电磁力方程和机械运动力平衡方程为
(5)
式中:X(s)为执行器换挡位移;FL为换挡过程中受到的阻力;m为执行器质量。
系统在设计时取最大电磁力系数kmax,由式(1)可知在不同时刻下驱动力相较于理想驱动力的差值Floss为
Floss=[f(x(t))-kmax)]i(t)。
(6)
执行器需要具备高速度的工作要求以及定位的高精度要求,设计前馈补偿装置对执行器输出损失力进行提前补偿,消除部分驱动力扰动引起的执行加速度变化,执行器加速度a(s)为
(7)
若令
Gn(s)=-(Ls+R)/ke,
(8)
则必有a(s)=0,式(8)为对扰动的全补偿条件,但是由于式(8)的分子次数高于分母,不便于物理实现,若令
(9)
则Gn(s)在物理上能够实现,且能够近似满足执行器力损失全补偿要求。驱动装置在运行过程中会产生损耗,损耗作为热源以热量的形式散发,最终导致温度的升高。对于驱动装置来说,驱动力的大小主要取决于永磁体的磁性能,为了保证永磁体的高温性能,选择了具有较高矫顽力的烧结汝铁棚材料,该材料最高工作温度为150 ℃。不同温度下永磁体的磁通密度B为
B=f(H,T)=Br[1+α·(T-T0)]+
(10)
式中:Br为室温剩余磁感应强度;α为剩磁Br在工作范围内的平均可逆温度系数;μ0为真空磁导率,也称磁性常数;Hcb为矫顽力。在不同温度下,永磁体N42SH的剩磁和矫顽力分别为:
Br(T)=Br0×[1+α(T-T0)],
(11)
(12)
针对执行器在换挡过程中的驱动力波动及永磁体性能下降问题,提出一种基于执行器工作特性的补偿控制策略,补偿结构如图7所示。
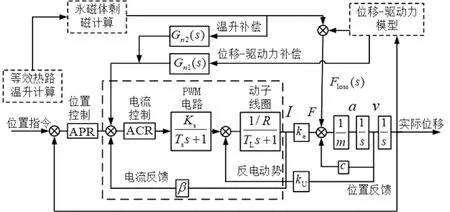
图7 执行器工作特性补偿控制结构图
图7的补偿控制逻辑为,当汽车收到驾驶员换挡指令时,控制器将换挡位移量作为控制目标量,位置、电流双闭环控制器分别对输入与反馈信号的偏差进行计算得到PWM变换器控制电压,经PWM电路放大得到的执行器电枢电压加载到执行器电路中,动子线圈通电后在磁场中受到的洛伦兹力作为换挡驱动力带动结合套运动进行换挡。执行器运动过程中受到的阻尼力和产生的反电动势会反作用于系统中,影响换挡力和换挡电压。在执行器工作期间,不同位置下驱动力会发生改变,同时执行器各部件产生的损耗会导致永磁体温度升高导致永磁体磁力衰退,使得执行器换挡驱动力下降。根据本文拟合得到的执行器位移-驱动力模型以及温升模型计算出执行器在换挡过程的不同位置及不同时间下驱动力损失,通过前馈环节对换挡电压进行提前补偿,降低驱动力下降对换挡时间的影响。
4 结果与分析
为验证补偿控制对执行器的有效性,搭建了如图8所示的实验平台,通过基于DSP2812的控制器实现补偿控制算法,执行器位移信号通过线圈骨架上的直线位移传感器实时监测并显示在上位机中。执行器换挡工作行程为18 mm,执行器质量m= 0.29 kg;线圈电感L= 4.8 mH,线圈电阻R= 5.5 Ω。

图8 实验平台
分别测试PID控制及补偿控制对阶跃目标响应的控制性能,图9为给定位置18 mm阶跃信号,常温下不同控制系统的执行器位置跟踪曲线。
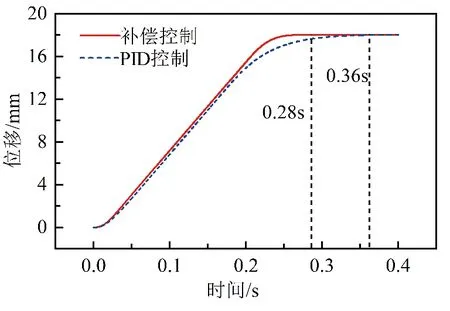
图9 位移随时间变化曲线
由图9可知,PID控制和补偿控制在给定阶跃信号下都能迅速无超调跟踪,基本无稳态误差。其中,PID控制的响应时间为0.36 s,而补偿控制的为0.28 s,响应速度相比于PID控制提高了22%。通过曲线对比可知,PID控制和补偿控制都能实现较好的控制稳定性,但补偿控制通过前馈环节提前对换挡过程驱动力衰退进行补偿,具备更高的阶跃目标位移响应性能。
为验证不同控制方法对于永磁体温度升高引起磁性能衰退的控制效果,图10为执行器连续工作10 min后,永磁体温度达到45 ℃时,执行器采用不同控制方法换挡力随时间变化情况。从图10可以看出,随着永磁体温度升高,执行器换挡力发生衰退,两种控制方式的换挡时间都有所增加,PID控制的增加至0.41 s,补偿控制的为0.33 s,换挡速度提高了20%。
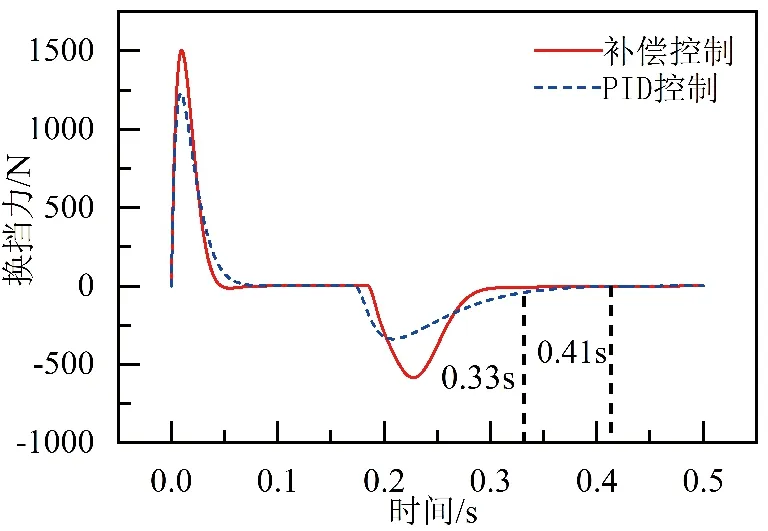
图10 换挡力随时间变化曲线
图11、12分别为执行器在常温和45 ℃时,执行器由于位置变化和永磁体温升引起的驱动力衰退变化以及补偿控制补偿力随时间变化情况。
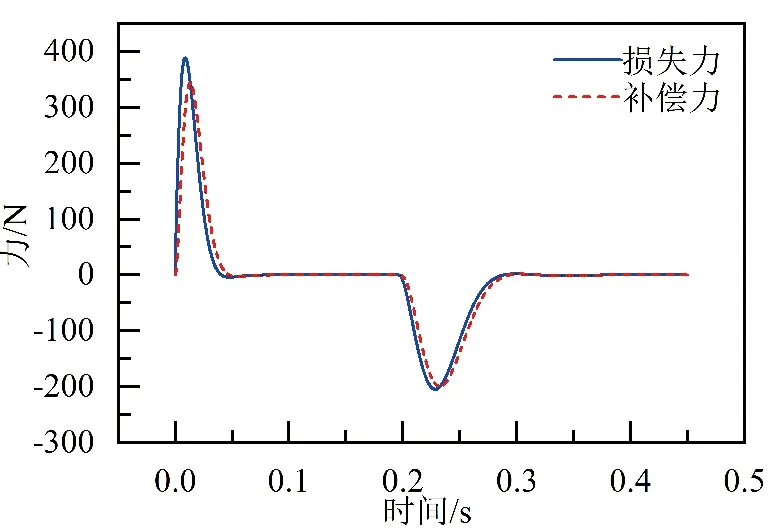
图11 常温下损失力与补偿力变化曲线
从图11、图12可以看出,执行器常温及45 ℃执行器最大损失力分别为390、590 N,最大补偿误差为13%,其余时间点补偿控制可以有效跟踪执行器工作特性引起的驱动力损失问题,补偿误差均在5%以内;在执行器换挡加、减速阶段驱动力波动较大,这一阶段补偿控制作用明显,在匀速阶段驱动力波动较小,PID控制可发挥自身调节作用对驱动力波动进行抑制。
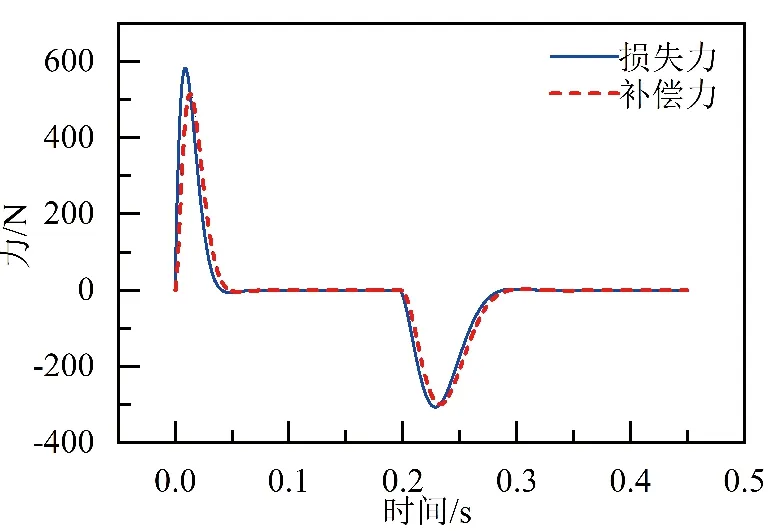
图12 45 ℃下损失力与补偿力变化曲线
5 结论
1)针对执行器驱动力随位移变化工作特性,拟合出了驱动力随位移变化数学模型;针对执行器损耗引起的永磁体温升工作特性,设计了执行器四热源等效热路,可实时计算执行器在工作状态下的驱动力变化。
2)设计了一种基于执行器工作特性的补偿控制方法,相比于传统PID控制,补偿控制可使执行器的换挡速度明显提升,结果表明,永磁体在常温和45 ℃温度下,补偿控制相比于PID控制,换挡速度分别提升了22%和20%。

