立足本手 巧构妙手 释疑俗手*——以一道对称双变量条件最值问题为例

安恺凯 沈丹丹

江苏省无锡市东北塘中学 (214101)江苏省天一中学 (214101)

2022年语文新高考Ⅰ卷以围棋的三个术语“本手、妙手、俗手”为作文题目，其中本手是指合乎棋理的正规下法；妙手是指出人意料的精妙下法；俗手是指貌似合理，而从全局看通常会受损的下法.笔者由此想到，在数学的解题教学过程中，不也会经常遇到的正规解法、精妙解法、以及貌似合理却错误的解法吗？笔者便从“本手、俗手、妙手”三个角度分别入手，来探究一道对称双变量条件最值问题，现整理如下，以飨读者.

1 问题呈现

问题1 设实数a，b满足a+b=6，则(a2+4)(b2+4)的最小值为.

这是一道题既简洁又优美的双变量函数的条件最值问题，其优美感来自于代数结构中的对称性，即在条件和结论中，任意交换两个变量都不会改变条件和目标函数.然后在这道试题简洁优美的外表下，却隐藏着有一个极具诱惑性的“俗手”，即通过令两个对称变量相等来求出最值，文献[1]称这种方法为对称变量法.在一次测试中，不少学生便把a=b=3代入目标函数求得最小值为169，测试情况反映出对称变量法这招“俗手”具有明显的普遍性，也反馈出该类型问题具有一定的深度探究价值.

2 立足本手 风光不与四时同

问题2 设实数a，b满足a+b=m(m>0)，则当t>0时，f(a,b)=(a2+t)(b2+t)的最小值为，此时实数a，b的值分别为.

本手1 代入消元

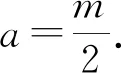
本手2 整体换元

本手3 对称换元

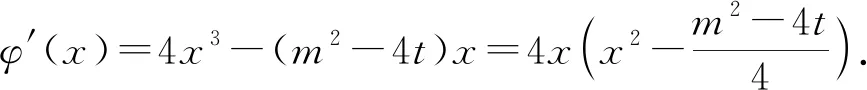
“本手1”通过代入消元法将目标函数转化为四次函数；“本手2”通过整体换元法将目标函数转化为二次函数；“本手3”通过对称换元法将目标函数转化为四次偶函数.同是减元的解题思路，却呈现出不同的表现形式，正所谓“风光不与四时同”.教师在带领学生领略各种方法不同“风光”的同时，也应注重引领学生看透问题本质，即三招“本手”都立足于将双变量问题转化为单变量问题，继而转化为对应的函数关系式，同时题目中的约束条件也随之转化为函数的定义域，最终利用相应的函数单调性来分析与讨论.

基于以上多角度解析，我们得到如下结论：

3 巧构妙手 观物行成有七易

妙手 以形探数

图1

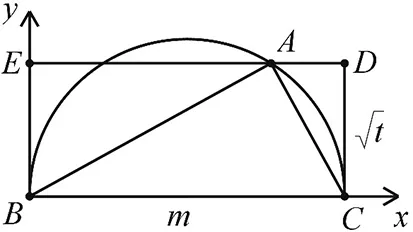
图2

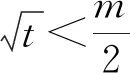
图3

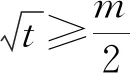
“观物取象”强调的是数与形之间的联系.从“观物”到“取象”，旨在培养学生从观察代数式的结构特征，到构造相应几何模型的关键能力.本题便可根据题目条件，结合代数式的几何意义，合理抽象，通过数形结合，将复杂的代数问题有效转化为动态几何下的三角形面积的最值来分析与处理.将抽象的数量关系直观形象化，以形探数，思维巧妙，视角特殊，不失为一招“妙手”.

4 释疑俗手 识得庐山真面目

基于以上“本手”与“妙手”的多角度解析，“俗手”的错因也得到了多方位的辨析.但“俗手”的成因又由何而来，此类对称双变量条件最值问题又源起何处？笔者在“本手3”中汲取到灵感，从四次偶函数的角度再探此类问题的“庐山正面目”.

图4

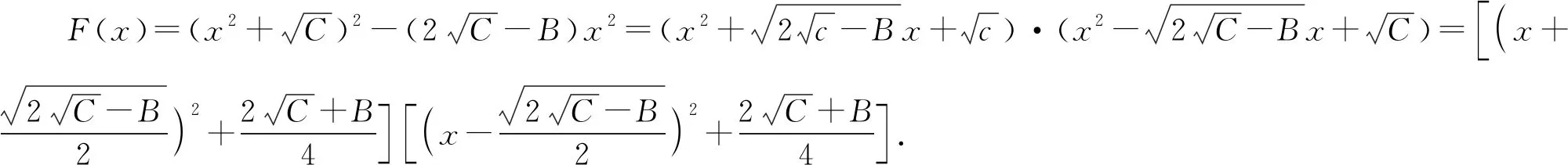
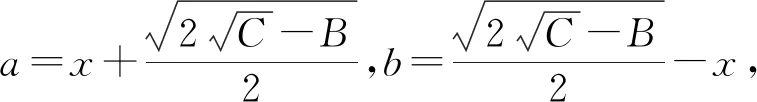
5 结语

2022年语文新高考Ⅰ卷对“本手、妙手、俗手”有如下阐述：“本手是基础，妙手是创造.一般来说，对本手理解深刻，才可能出现妙手；否则，难免下出俗手，水平也不易提升.”在数学的解题教学过程中也正是如此，教师首先应当立足于“本手”，即立足于“四基”，引导学生理解基础知识、习得基本技能、感悟基本思想、积累基本活动经验，从而形成规范化思考问题的品质；其次应注重在解题教学过程中合理体现几何直观与代数运算之间的相互融合，即通过形与数的结合，感悟数学之间的关联，加强对数学整体性的理解，从而实现解题教学由“知识立意”向“能力立意”的转变，以此才能促使学生在解决具体问题时，从不同角度来巧施“妙手”.同时“俗手”亦有丰富的思维价值，通过对“俗手”的错因与成因的深度探究，可养成一丝不苟、严谨求实的科学精神，也有利于提高学生的独立思考能力.