从试验到论证——对一道数列问题的探究与思考

金永涛

北京理工大学附属中学 (100089)

数学试验，是在综合解决学习任务时，根据问题情境，构造出具体的实例或反例、发现或猜测实例蕴含的性质，通过进一步检验、归纳与推广等过程，实现对学习任务的深刻理解的数学学习活动.数学试验，要从观察数学对象开始，是数学学习、数学探究与数学研究的基础.

高中阶段对数列的研究是以“背景——概念(定义、表示、分类)——性质——特例”为基本架构，其中“特例”是指等差数列、等比数列这两类有明确的现实背景、可以给出精确的规律表达、在解决实际问题和数学问题中有重要应用价值的数列，对它们的研究按照“背景——概念——表示——性质——求和公式——应用”的路径展开.在研究一个具体的数列时，先要识别它是否为等差数列或等比数列；如果不是，可否将其转化为这两类特殊数列；问题中的数列与两类特殊数列具有哪些联系，怎么应用它们之间的联系思考、解答问题；如何应用数列的研究方法，探究与思考数列问题等.数列是一类特殊的函数，在思考数列问题时，要关注自变量的离散性和有序性，重视应用数学试验探究，积累数学活动经验并解答问题.

一、问题呈现

题目已知数列{an}，a1=1，an+1+an=3n+1，求{an}的通项公式与前n项和Sn.

本题中数列以递推关系的形式给出，根据递推关系可以依次得到{an}每一项的值；在递推关系中，相邻两项之和为3n+1，注意到数列{an+1+an}是一个等差数列.

二、问题探究

要求{an}的通项公式与前n项和Sn，首先要准确认识、理解数列的性质，根据递推关系，通过列举法，观察、分析{an}部分项的值，探究数列的性质并解答问题.

探究1：列举{an}部分项的值，探究数列的性质.

a1=1，a1+a2=4，a2+a3=7，a3+a4=10，a4+a5=13，a5+a6=16，a6+a7=19，a7+a8=22，a8+a9=25，….

易得到数列{an}为1，3，4，6，7，9，10，12，13，….即该数列的奇数项是以1为首项，以3为公差的等差数列；偶数项是以3为首项，以3为公差的等差数列.

探究2：归纳推理，确定研究思路与方法.

通过分析数列的奇数项、偶数项的关系——等差关系，概括出{an}的性质为a1=1，a2=3，且an+2-an=3.借助数学试验(列举与归纳)探究数列性质，这是研究数列问题的重要方法；依据得到的性质，整理递推关系，确定出解决问题的具体方法.

探究3：逻辑推理，回归概念本质.

在递推关系中，数列{an+1+an}也可以看成是一个数列且为等差数列，根据等差数列的概念可知，从第二项起后一项与相邻的前一项之差为常数(公差)，则(an+2+an+1)-(an+1+an)=[3(n+1)+1]-(3n+1)，化简后也能得到an+2-an=3.这一过程，是基于“数列的递推关系也是一个数列”的学科观点，应用数列概念本质确定出研究思路与解决方法.

探究4：严谨论证，提升素养.

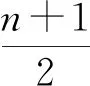
探究5：转换视角，提炼学科思维.

在求解数列问题时，通常利用数列的通项公式或递推关系求解前n项和Sn，或者是先求出数列的前n项和Sn，再进一步求解通项公式.之所以能这样思考，不仅是源于an和Sn的基本关系，也是对数列概念本质的思考——前n项和是一个数列{Sn}.

三、思考与感悟

数学试验是研究数列的重要方式，对于复杂的数列问题，直接进行推理论证是困难的.数学试验，既是准确把握题目信息、深入认识数列规律的重要方式，也是探索研究思路和具体解决方法的基础.数学试验不能只停留在对数学对象的感性认知层面，还要对数学对象的内在规律进行深层次的探究，并借助推理论证、数学运算实现对数学对象的性质、规律的严谨说理.

在求解数列问题时，要重视对数列基本特征的认识和理解，这是有效解答数列问题的根本.通过将数列的递推关系转化为特殊数列(等差数列、等比数列)的关系，或构建起其与特殊数列的内在关联，进而应用典型方法(如公式法、迭代法等)求解数列的通项公式及前n项和.在解题过程中，不仅要准确掌握并应用递推关系、通项公式与前n项和公式思考并解答问题，还要有意识地构建、形成数列的学科观点——递推关系与前n项和也是一个数列，以数列的视角看待递推关系与前n项和，系统掌握数列问题的研究方法.