扭摆式多方向压电振动俘能器的研究

阚君武 吴亚奇 张忠华 何恒钱 孟凡许

1.浙江师范大学精密机械与智能结构研究所，金华，321004 2.浙江省城市轨道交通智能运维技术与装备重点实验室，金华，3210043.浙江清华柔性电子技术研究院，嘉兴，314006

0 引言

为实现传感器的能量自给、避免废弃电池污染环境，基于电磁、摩擦、压电等原理的微小型俘能器的研究成为国内外的前沿热点[1-5]。每一类微型俘能器都有其自身的优势和适用领域[6]，压电俘能器的优势在于结构简单、无电池干扰、易于实现结构上的微小化，故其适用范围更广，已逐步用于俘获自然环境中振动能[7]、人体动能[8]、旋转机械动能[9]及流体动能[10]等能量。这些能量最终都是通过压电振子的振动转化为电能[11]。

传统的压电振动俘能器大都采用端部固定有质量块的压电振子作为换能部件，所适应的振动方向单一、有效频带窄，无法满足多向振动、频率变化范围较大场合的传感器自供电需求[12]，故国内外学者将研究重心转向多方向振动俘能器。WANG等[13]将PVDF压电薄膜粘贴于悬臂圆柱的根部用以发电，以便有效捕获多方向的振动能量，但该俘能器仅在一个共振峰下工作，有效频带窄。ZHAO等[14]设计了一种空间螺旋结构的俘能器，可沿空间多个方向伸缩、弯扭变形，对空间各方向均有较好的输出响应，然而，其压电振子工作时产生双向弯曲变形，压电片承受交变的拉-压应力，易因变形过大而损毁。CHEN等[15]在空间多个方向上布置了悬臂梁压电振子，某一方向的振动都能使部分压电振子产生响应，但压电振子密度过大时会相互干涉。YUAN等[16]提出了一种基于并联机构的六自由度俘能器，可实现多向振动能量的收集，但结构过于复杂。ALGHISI等[17]提出一种撞击式多方向振动俘能器，利用自由运动的钢球撞击各侧面上设有压电振子的框架结构发电，但工作的撞击不仅会产生噪声，也易导致压电晶片脱落。

在总结分析国内外研究现状的基础上，为实现多方向振动能量的有效回收，提高俘能器的多方向振动响应能力及可靠性，本文提出一种扭摆式多方向压电振动俘能器，并从有限元仿真与试验两方面进行了研究。

1 俘能器的结构及原理

扭摆式多方向压电振动俘能器的结构原理如图1所示，主要由压电振子、弹性梁、锤头、摆杆和压块组成。锤头、摆杆和弹性梁构成激励器。压电振子由金属基板与压电晶片粘接而成，压电振子的自由端经压块顶靠在弹性梁上。

(a)结构原理

(b)一阶谐振 (c)二阶谐振图1 俘能器结构示意图Fig.1 Structures diagram of energy harvester

当俘能器受到某一方向的激振力时，激励器在惯性力的作用下产生扭摆变形，通过弹性梁迫使压电振子产生单向弯曲变形而发电。因压电振子的弯曲变形是由弹性梁间接接触导致的，当弹性梁发生多阶变形时压电振子都以上下弯曲变形为主，使压电晶片仅沿压应力单向变形，故所受拉应力较小。

2 有限元仿真分析

目前，难以建立一个精确的解析模型来进行俘能器振动模态及动态响应特性分析，故本文通过有限元建模仿真方法进行研究，所建立的COMSOL有限元模型如图2所示，其坐标系原点为弹性梁的几何中心。根据有限元仿真的需要，将弹性梁夹持区域端点作为后续绘制动力学响应曲线的位移参考点，通过该点在Z轴方向上的位移来表征俘能器的输出电压。仿真中涉及的相关结构参数如表1所示。

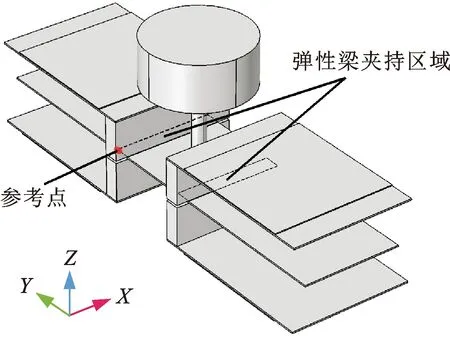
图2 有限元几何模型Fig.2 Finite element geometric model

图3给出了俘能器的模态振型，其中图3a、图3b分别为激励器绕Y轴和X轴扭转的模态振型，所对应的固有频率分别称为第一、二阶固有频率，其仿真结果分别为fn，1=35.4 Hz和fn，2=52.9 Hz。俘能器受到某一方向的激振力时，激励器激励压电振子使其发生弯曲变形。因压电振子端部顶靠在弹性梁上，故激励器发生第一阶和第二阶谐振时，压电振子仍以弯曲变形为主。

表1 仿真涉及的相关结构参数

(a)一阶振型 (b)二阶振型图3 俘能器的模态振型Fig.3 Modal shapes of the energy harvester

为便于叙述，将激励器振动方向(激励方向)与X轴在XOY平面内的夹角θ称为激励角。图4为不同激励角时俘能器的动力学响应曲线。图中曲线的变化趋势表明：激励角变化对两阶谐振频率影响均较小，但对输出电压的影响较大且影响规律不同。激励角从0°增加到90°时，第一阶谐振电压减小，激励角θ=90°时因电压较小而未显现，第二阶谐振电压增大，激励角θ=0°时因幅值较小而未显现。

图4 激励角不同时俘能器的动力学响应特性曲线Fig.4 Dynamic responses of the energy harvester when the angle of excitation changes

图5为不同激励角θ时第一阶和第二阶谐振峰幅值(D1和D2)的变化曲线。图中曲线在360°的角度范围内关于0°-180°直线及90°-270°直线对称，即每90°对称循环一次。在整个角度变化域内，俘能器的最大响应位移构成图中曲线的包络线。显然，在XOY平面内俘能器响应无死角，即该俘能器理论上能对水平面内任意方向的振动能量做出有效响应。

图5 激励角不同时谐振峰幅值的变化曲线Fig.5 The change curves of resonance peak of the energy harvester when the angle of excitation changes

3 试验测试与分析

为探究压电振动俘能器的输出特性并验证仿真结果的正确性，设计制作了图6所示的试验测试平台。试验仪器主要包括ECON VT-9008/8振动控制器、Premax VSA-L800A功率放大器、Premax LT-50ST振动台、Rigol MSO6014A 型混合信号示波器、变阻箱等。试验样机主要由压电振子、弹性梁、锤头和摆杆组成，见图7。压电振子尺寸为35 mm×25 mm×0.3 mm，压电晶片为φ35 mm×0.2 mm，激励器中弹性梁尺寸为85 mm×20 mm×0.3 mm，摆杆为φ3 mm×50 mm，扭摆半径为20 mm，附加25 g锤头。试验结构参数与仿真所用的结构参数一致。试验中，通过调整样机的安装方位来改变激励角。

图6 测试平台Fig.6 Testing platform

图7 试验样机Fig.7 Test prototype

根据仿真结果，激励角不与X、Y轴重合时俘能器会出现两个谐振峰。以θ=45°为例，得到图8所示的两个谐振频率处的电压波形。由图8可知，俘能器发生第一阶谐振(40 Hz)时，在140 ms的时间跨度内俘能器的电压波形数量为10或11，而振动信号的理论波形数量是5.6，二者约为2倍关系。这是因第一阶谐振时，激励器沿着X轴左右扭摆，一个周期内弹性梁对单片压电振子进行两次激励。俘能器发生第二阶谐振(53 Hz)时，激励器沿着Y轴前后扭摆，此时一个振动周期内激励器对压电振子仅产生一次激励，因此波形数量与激励频率一致，理论波形数量为7.42，实际波形数量为7或8，图中明显较小的波形为振荡所致。

图8 电压波形图Fig.8 Voltage waveform

根据仿真结果，当激励角变化时，两阶谐振峰变化曲线每隔90°对称循环一次，故试验中着重研究θ=0°～90°的幅频特性。图9给出了不同激励角时输出电压的幅频特性曲线。图9与图5的结果均表明：激励角变化对两阶谐振频率影响较小，但对其输出电压的影响较大且影响规律不同。图9出现了仿真中并未出现的波动以及幅值大小的改变，该现象可能的原因为加工和安装误差以及压电振子与弹性梁接触等不可控因素的存在。根据试验结果，俘能器的第一、二阶谐振频率分别为40 Hz和53 Hz，这与仿真结果基本一致。

图9 激励角不同时输出电压的幅频特性曲线Fig.9 The change curves of output voltage versus frequencies of the energy harvester when the angle of excitation changes

为方便叙述，将第一阶和第二阶谐振频率(fn，1，fn，2)对应峰值电压分别称为第一阶和第二阶谐振电压(Un，1，Un，2)。图10给出了两阶谐振电压与激励角的关系曲线，图11给出了两阶谐振频率与激励角的关系曲线。由图中曲线的变化趋势可以看出，激励角对谐振频率影响较小，对谐振电压影响较大；随激励角θ增加，第一、二阶谐振频率几乎不变，但其对应的谐振电压不同，即第一阶谐振电压Un，1降低且降低速率逐渐增大，第二阶谐振电压Un，2升高且升高速率逐渐减缓；存在激励角θ=44°使得两阶谐振电压相等(Un，1=Un，2)，当θ<44°时Un，1>Un，2，当θ>44°且其他激励条件不变时Un，1

图10 激励角对谐振电压的影响Fig.10 The relation curve of excitation angle to resonance voltage

图11 激励角对谐振频率的影响Fig.11 The relation curve of excitation angle to resonance frequencies

随激励角θ增加，Un，1降低、Un，2升高的原因在于：当θ=0°时，激振力F沿X轴方向，俘能器绕着Y轴扭摆相对较大，故第一阶谐振峰幅值较大；同理，当θ=90°时，激振力F沿Y轴方向，第二阶谐振峰幅值最大。θ=0°时出现微小第二阶谐振峰及θ=90°时出现微小第一谐振峰的原因可能是制作及安装误差所致。

以上给出的是俘能器输出电压的特性，当俘能器所生成的电能不被实时利用时，需进行存储。为获得电容储能特性，选取容量为470，1100，2200 μF的电容进行了充电试验。图12和图13分别给出了(θ=0°、f=40 Hz)和(θ=90°、f=53 Hz)情况下充电特性曲线。由图可知，在电容饱和时充电时间随电容容量的增加而增长，但所达到的饱和电压基本相同。①θ=0°、f=40 Hz时，容量为470，1100，2200 μF的饱和充电时间为200，300，600 s，所对应的电压分别为18.8，18.8，19 V，即分别储存能量0.083，0.194，0.397 J；②θ=90°、f=53 Hz时，容量为470，1100，2200 μF的饱和充电时间为180，360，660 s，所对应的电压分别为19.2，19.2，18.8 V，即分别储存0.087，0.203，0.389 J。根据试验结果，沿X轴和Y轴方向激励时，电容的存储速度分别达到0.58 mJ/s和0.54 mJ/s。

图12 沿X轴方向激励时电容的充电特性曲线Fig.12 The charging curves of the energy harvester under X-axis excitation

图13 沿Y轴方向激励时电容的充电特性曲线Fig.13 The charging curves of the energy harvester under Y-axis excitation

除了输出电压、电能存储外，输出功率是评价俘能器发电能力的又一关键要素。图14给出了沿X轴和Y轴激励时各压电振子的平均功率P与负载电阻R的关系曲线。由图可知，沿X轴和Y轴激励时，均存在两个最佳负载使输出功率最佳。沿X轴方向激励时，两个最佳负载电阻及其所对应的最佳功率分别为(17，81)kΩ和(4.56，3.4)mW；沿Y轴方向激励时，两个最佳负载电阻及其所对应的最佳功率分别为(17，61)kΩ和(3.96，3.89)mW。上述试验中，单一激励方向时出现两个最佳负载的可能原因在于：各压电振子自身动力学特性及阻抗特性存在一定的差异，弹性梁上下两侧压电振子初始受力状态有所不同。

图14 输出功率与负载电阻的关系曲线Fig.14 The change curves of output power versus load resistance

4 结论

为实现多方向振动能量回收，提出一种扭摆式多方向压电振动俘能器，通过锤头、摆杆和弹性梁构成的激励器间接、单向激励压电振子，优势在于：可收集水平面内任意方向的振动能量；弹性梁多阶模态振动时压电振子均发生单向弯曲变形，所受拉应力较小。从有限元仿真和试验两方面对其进行了研究，获得了激励方向不同时输出电压、电容充电及输出功率特性，具体结论如下：

(1)俘能器可回收平面内任意方向的振动能量，但不同激励方向发电特性不同。激励角在0°～360°变化时，各阶谐振峰每隔90°对称循环一次；激励角从0°增加到90°时，第一、二阶谐振频率均基本不变，但其所对应的谐振电压变化不同，即第一阶谐振电压降低且降低速率逐渐增大，第二阶谐振电压升高且升高速率逐渐减缓。存在激励角θ=44°使得两阶谐振电压相等。

(2)电容饱和充电时间随电容容量的增加而增长，但所达到的饱和电压基本相同。沿X轴方向激励时，容量为470，1100，2200 μF的电容饱和充电时间为200，300，600 s，所对应的电压分别为18.8，18.8，19 V；沿Y轴方向激励时，容量为470，1100，2200 μF的饱和充电时间为180，360，660 s，所对应的电压分别为19.2，19.2，18.8 V。沿X轴和Y轴方向激励时，电容的存储速度分别达到0.58 mJ/s和0.54 mJ/s。

(3)沿X轴和Y轴激励时，均存在两个最佳负载电阻使输出功率最佳。沿X轴方向激励时，最佳负载电阻及其最佳功率分别为(17，81)kΩ和(4.56，3.4)mW；沿Y轴方向激励时，最佳负载阻值及其最佳输出功率分别为(17，61)kΩ和(3.96，3.89)mW。