工业装配抗振外骨骼的动力学仿真及试验研究
陈俞鹏 王海波 薛朝军 邹怀静 高依民
1.西南交通大学机械学院,成都,6100312.轨道交通运维技术与装备四川重点实验室,成都,610031
0 引言
制造业转型升级浪潮下,自动化设备不断涌现并逐步取代人工操作,但手持式工具学习成本低、可靠性高、灵活性高等特点使其在航空、建筑、林业等领域的应用比例仍居高不下[1]。飞机装配过程涉及大量的手工铆接操作,据统计,一架支线飞机上有几十万颗铆钉,而一架大型干线飞机上有几百万颗铆钉[2]。铆枪、冲击钻等手持式工具作业时会产生强烈的振动[3],长期从事手传振动作业容易导致手臂系统血管、神经的病变和肌肉骨骼疾病即手臂振动综合征(hand-arm vibration syndrome,HAVS)[4]。振动性白指是HAVS常见的发病表现[5],其患指症状为受冷时出现麻木、刺痛等感觉[6],严重时导致握力下降。某飞机装配厂调查发现工人自述的肌肉骨骼患病率达到90.2%[7]。就工人而言,手传振动危害身体健康,影响生活质量;从企业、国家角度看,手传振动造成巨大经济损失。
针对手传振动的防控措施包括振源消除、工具改进、行政管控、穿戴个体防护装备,目前学者多从改进现有工具及开发个体防护装备的角度进行研究。JING等[8]在人与工具之间引入X形非线性减振结构来解决手持式拆除工具的减振问题。LINDELL等[9]在捣固机、破碎机等手持式冲击工具的壳体与执行机构之间引入辅助质量块来实现非线性减振,优化后的工具可在较宽的工作频带内减小操作人员的振动。JAIN等[10]通过考虑手的解剖形状,开发出符合人体工程学的工具手柄,与圆形手柄相比,人体工程学手柄的振动减小量为7.27%~14.59%。RENS等[11]指出防振手套这类个体防护的装配减振效果与频率相关,仅能减少较高频率(超过500Hz)的振动分量。
改进振动工具的成本高、普及周期长,防振手套的减振效果有限,现有抗振措施难以满足装配业抗振及作业效率提升的需求。笔者针对航空装配的铆接工作,设计出一套具有减振与工具支撑功能的上肢穿戴抗振外骨骼,以减小振动伤害、提高可持续作业能力。利用ADAMS参数化动力学仿真模型与交互正交试验,优化外骨骼剪式减振单元结构参数。物理样机试验验证了外骨骼的抗振效果,并能客观评估外骨骼的减振及辅助性能。
1 抗振外骨骼的结构
上肢抗振外骨骼应具备减振、工具支撑、多人适配等功能,以适应振动工具复杂的使用工况。笔者根据成年人人体尺寸及人体百分位数应用通则,基于人机工程学设计方法,采用双百分位数限值设计外骨骼。
如图1所示,抗振外骨骼结构由前臂减振系统(对称剪式减振单元、夹持装置)、上臂支撑系统(肩关节、活塞式阻尼器、旋转式阻尼器、肘关节)、上肢穿戴系统(背带、背部支撑板)组成,通过上肢穿戴系统的可调背带和背部支撑板实现人体与外骨骼的绑定。上肢支撑系统的肩关节和肘关节处装有阻尼器(提供阻尼力矩)。支撑外骨骼前臂减振系统可实现工具支撑。前臂减振系统设有对称布置的剪式减振单元;剪式减振单元上下铰接弹簧阻尼减振器,作业时,工具产生的振动冲击由夹持装置、可调连杆依次传递至减振单元;减振单元内置的弹簧阻尼减振器可减小冲击,减少人体的振动暴露伤害。

图1 上肢抗振外骨骼结构Fig.1 Upper limb anti-vibration exoskeleton structure
2 动力学理论分析
为准确分析影响外骨骼减振性能的主要参数,结合抗振外骨骼的穿戴方式,假设人体手握振动工具,以完成姿势准备后的状态为初始系统平衡位置,建立人机耦合系统力学模型。图2中,U、V、W分别代表外骨骼的肩关节、肘关节、腕关节;l1~l5分别为连杆AW、AB、BD、GV、UV的长度;θ1~θ3分别为外骨骼肩关节、肘关节及剪式结构的夹角;k1、k2为剪式减振单元前后减振器的刚度;c1、c2、cU、cV分别为减振单元前后两个减振器、外骨骼肩关节、肘关节的阻尼系数;k3、k4分别为人体上肢水平及竖直方向的等效刚度;c3、c4分别为人体上肢水平及竖直方向的阻尼系数;m1、m2分别为工具以及夹持装置的质量;FI、Farm分别为周期激振力和手臂初始作用力;x、y分别为工具水平、竖直方向的位移。
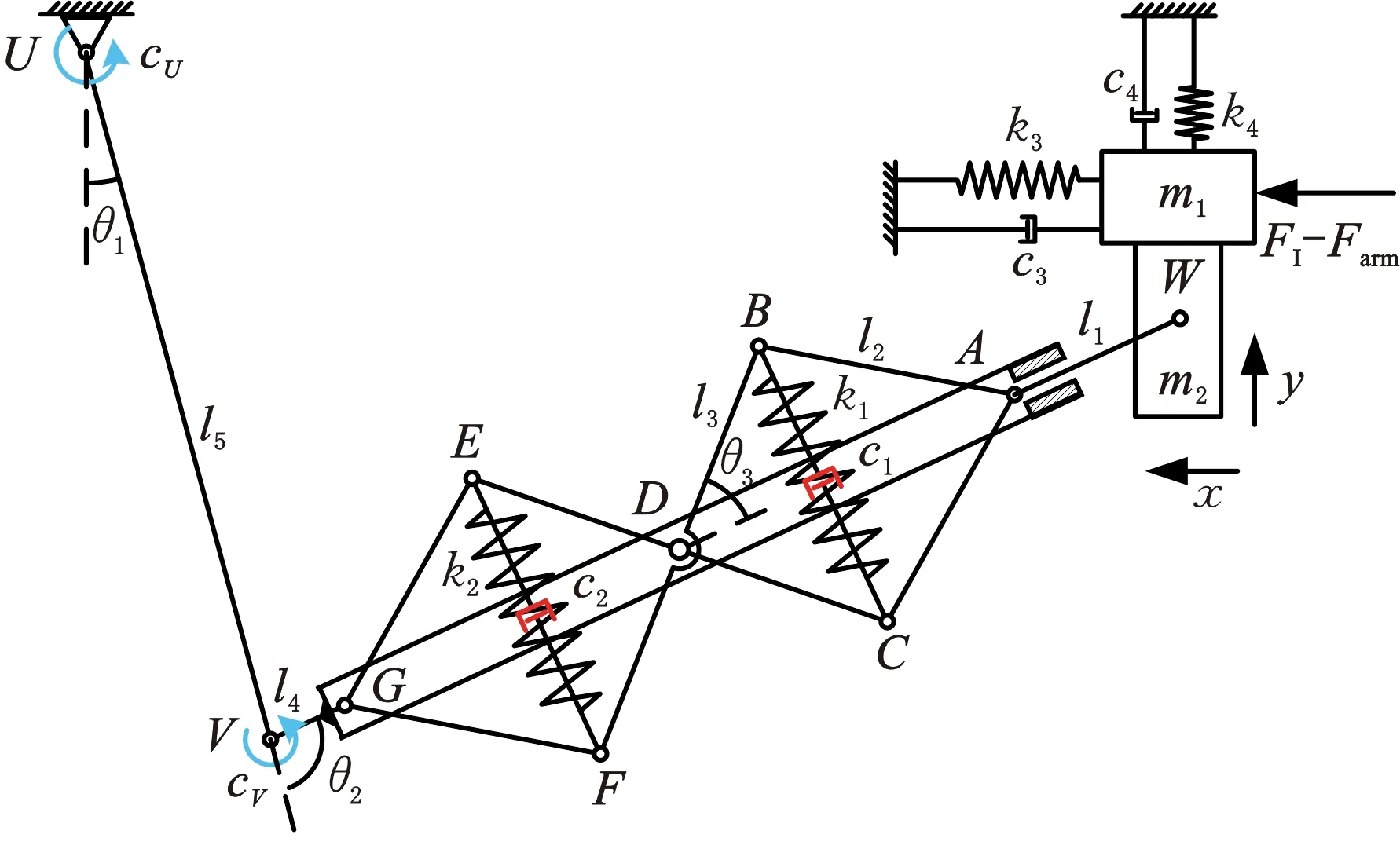
图2 人机耦合力学模型Fig.2 Human-machine coupling mechanical model
以W点为广义坐标原点,建立固于地面的坐标系,利用直角坐标法分析机构运动。由系统初始条件得到的参数有V点初始坐标(xV0,yV0),U点坐标(xU,yU),点V、W的初始距离lVW0,点A、D的初始距离lAD0,减振单元前后端弹簧初始长度lBC0、lEF0,关节夹角θ1~θ3。根据几何关系可得
(1)
由式(1)可知该系统为多自由度有阻尼强迫振动系统。根据图2,以x、y及任意时刻肩关节夹角θ为广义坐标,可设任意系统状态下W点的坐标为(x,y),V点的坐标为(xV,yV),其中,xV=xU+l5sinθ,yV=yU-l5cosθ。图3所示为剪式单元关于VW对称的连杆机构运动规律,接振时,连杆AB、BD发生偏转,点A、D共线且存在滑动副。

(a)实际轨迹 (b)假设轨迹图3 减振单元连杆运动规律Fig.3 Movement law of vibration damping unit connecting rod
由W、V点坐标及lVW0可得前臂长度
(2)
以及长度变化量ΔlVW。如图3b所示,假设D点固定,则点A、A′的距离ΔlVW/2=(lVW0-lVW)/2。设连杆BD的偏转角为α,则任意时刻连杆BD与点A、D所在直线夹角为θ3+α,任意时刻剪式单元前端弹簧长度为
lBC=2l3sin(θ3+α)
(3)
根据图3b,对于△A′B′D,由余弦定理可得
(4)
任意时刻弹簧长度lBC与初始弹簧长度lBC0的差值为剪式单元前后弹簧变形量s,即
s=lBC-lBC0
(5)
设外骨骼肩关节旋转角度为Δφ1、肘关节旋转角度为Δφ2,则有
(6)
根据拉格朗日原理建立人机耦合系统的运动微分方程:
(7)
L=Ek-Ep
式中,Ek为系统的动能;Ep为系统势能;ED为系统耗散能。
前臂减振系统两侧的减振单元有4个弹簧阻尼减振器,因此系统势能为
Ep=(k1+k2)s2+(k3x2+k4y2)/2
(8)
系统动能为
(9)
系统耗散能为
(10)
由系统动力学分析可知,外骨骼减振系统为非线性系统,其中,减振器弹簧刚度k1、k2影响系统势能;减振器阻尼系数c1、c2,外骨骼肩关节、肘关节的等效阻尼系数cU、cV影响系统耗散能。结构参数l1~l5通过影响减振器的变形量s及旋转角度Δφ1、Δφ2来影响系统的势能和耗散能。减振单元是影响系统减振性能的关键结构,故对其结构参数进行分析与优化。l1、l4、l5与人体手臂尺寸有关且穿戴时可调,cU、cV应根据支撑力矩以及操作舒适性选取,均为非减振单元参数,本文暂不展开。l2、l3的变化影响减振器在剪式结构中的安装位置,因此在保持减振器初始长度不变的条件用连杆长度比值l3/l2来描述减振器安装位置。由此可得l3/l2、k1、k2、c1、c2是影响外骨骼性能的减振单元关键参数。
3 减振单元优化设计
3.1 ADAMS参数化建模
根据工人作业时的手臂姿势及人机耦合力学模型,在ADAMS中建立图4所示的人机耦合仿真模型,按照设计参数设定抗振外骨骼的材料和质量,人体模型及关节阻抗参数按文献[12]设置。

图4 ADAMS仿真模型Fig.4 ADAMS simulation model
为分析参数值变化对减振性能的影响,降低ADAMS建模成本,对减振单元的局部进行参数化建模,其中,减振器弹簧的阻尼系数可通过定义设计变量实现参数化。
l3/l2需单独定义设计变量、参数坐标点、参数表达式实现参数化。根据图3所示的连杆结构间关系及图5所示的减振器安装位置Δx与l3/l2变化关系,并按下式在ADAMS中定义相应参数,实现模型参数化:
(11)
图5中,虚线代表某一l3/l2的减振器安装位置,最终的参数化建模结果如图6所示。

图5 连杆比值与减振器安装位置关系Fig.5 Ratio and shock absorber position relationship
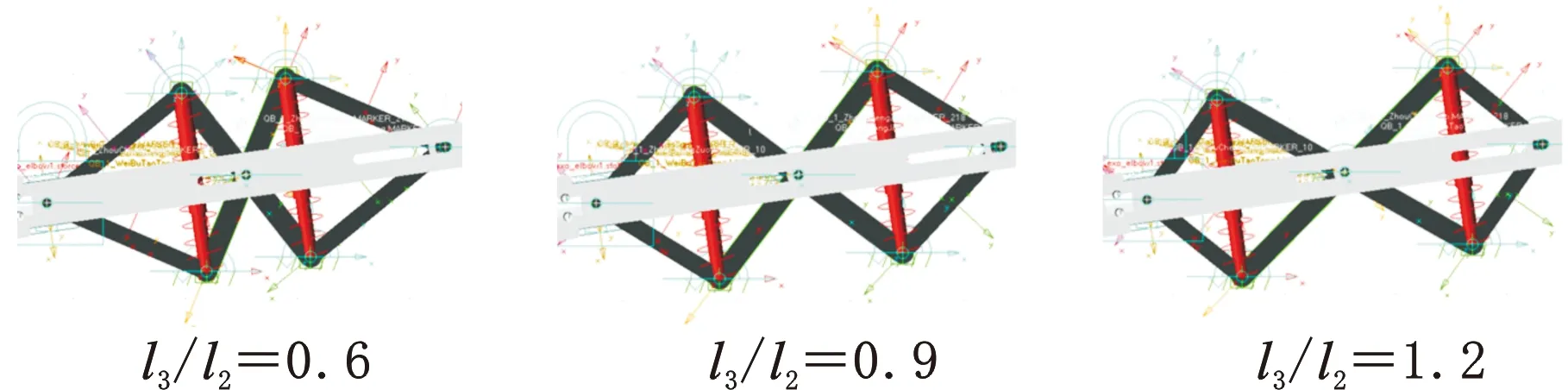
图6 局部参数化模型Fig.6 Local parameterized model
3.2 单因素振动响应分析
仿真的目的是研究减振单元各参数的变化对系统响应的影响,分析各参数较优的取值区间。不同型号铆枪的工作气压和冲击力大小不同,因此分别以50,100,150,200 N作为激励幅值F0,铆枪工作频率为25 Hz,设置周期激振输入为F0cos(50πt),采用控制变量法,按表1所示方案进行单因素振动响应仿真。

表1 单因素试验方案
作业过程中,振源与人手直接接触,因此选择腕关节受力F为测量指标。输入为周期信号,因此在ADAMS中定义测量函数截取稳态响应输出,取响应绝对值的最大值为幅值,以水平受力Fx和竖直受力Fy的合力幅值作为手部受力F。定义力传递率
TF=F/F0
(12)
单因素分析仿真结果如图7所示。

(a)k1,k2与力传递率关系

(b)c1,c2与力传递率关系
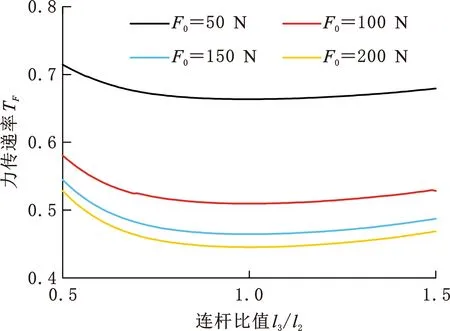
(c)l3/l2与力传递率关系图7 单因素分析结果Fig.7 Single factor analysis results
由图7a可知,随着弹簧刚度的增大,力传递率先减小后增大,但整体呈增大趋势。激励幅值分别为100,150,200 N时,最小传递率对应的弹簧刚度分别为0.3,0.5,0.7 N/mm,这说明激励幅值增大时可适当调大弹簧刚度。综上,为满足剪式单元功能的要求,弹簧刚度取值应在设计值附近。由图7b可知,阻尼取值在[0,1](N·s/mm)时,力传递率显著下降,在[1,10](N·s/mm)内缓慢下降直至基本不变,对比其他结构参数可以发现,阻尼对系统减振性能影响较大。激励幅值为150 N时,阻尼在在[0,1](N·s/mm)内的力传递率减小38.9%,在[0,10](N·s/mm)内的力传递率减小48.3%,因此,阻尼系数取1 N·s/mm可获得最优的减振器结构尺寸及力传递率。由图7c可知,l3/l2≈1时,各激振幅值下的力传递率较小,即阻尼器安装在中间位置的减振效果最好。
3.3 交互正交试验优化设计
由单因素分析可得各关键参数的推荐取值范围,但无法得出多个参数变化时系统的振动特性及参数的最优组合。因此本节利用ADAMS参数化模型,以M0501型铆枪的激励150 N为输入,采用正交试验法优化减振单元结构,选取最优的参数组合。剪式结构前后交叉,设计试验时有必要考虑因素的交互作用的影响[13]。由于交互项较多,因此根据L16(25)正交试验表,利用Minitab设计五因素两水平且考虑全交互作用的正交试验。本次仿真仅作交互分析,最佳水平组合方案通过去除不必要交互项,以腕关节受力为优化目标,以剪式单元结构参数为约束条件,五因素三水平正交试验获得的交互分析结果如图8所示。由图8可知,交互项k1×k2、l3/l2×c1、l3/l2×c2的曲线存在交叉。各交互项与主因素的影响显著性可通过方差分析获得。

图8 交互作用二元图Fig.8 Binary diagrams of interaction
由表2可知,交互项c1×c2的P值小于0.05,可判定为交互作用显著。综合各因素的F值可知,各主因素及其交互项对试验指标的影响显著性排序(由大到小)为:c2,c1,l3/l2,l3/l2×c2,l3/l2×c1,k1×k2,k2,k1,c1×c2。c1×c2,l3/l2×c1,l3/l2×c2的显著性较高,但其F值均小于l3/l2,c1,c2的F值,即交互项c1×c2,l3/l2×c1,l3/l2×c2对试验指标的影响作用低于主因素的影响作用,对最佳水平搭配无修正作用,而k1×k2的F值大于k1、k2的F值,因此设计试验时仅需考虑k1、k2之间的交互作用。根据单因素分析结果及试验表列数限制,最终设计五因素三水平一交互的正交试验,各因素水平值如表3所示。
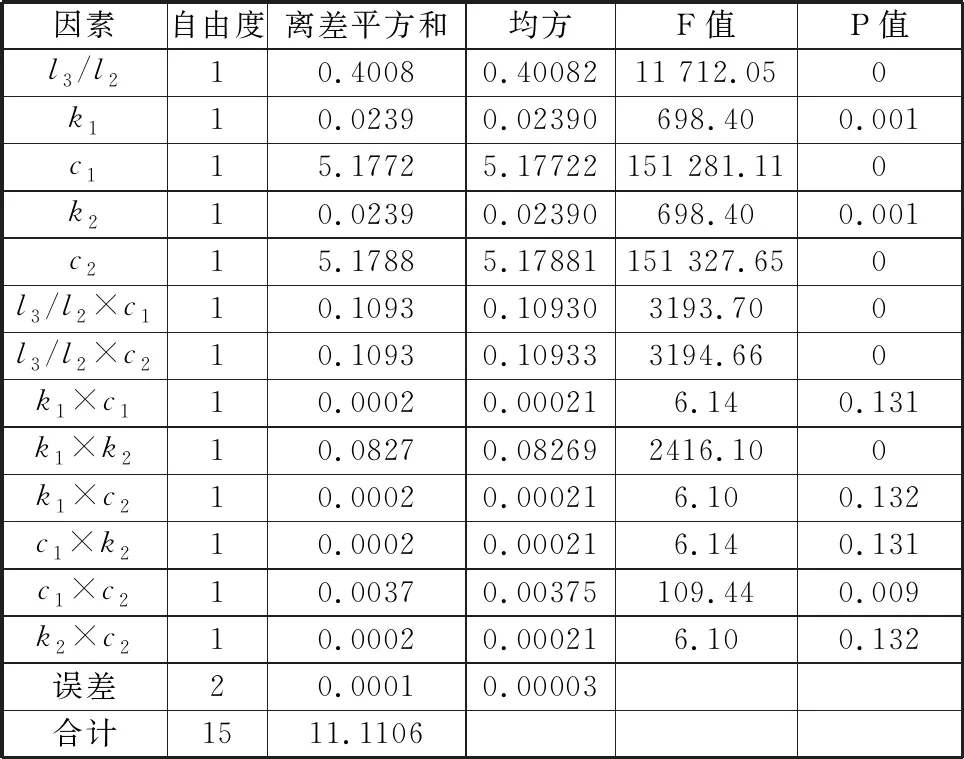
表2 方差分析

表3 因素水平表
使用Minitab选取L27(313)标准正交表并设置交互项,生成试验方案,利用ADAMS/insight模块按方案依次仿真,部分试验结果如图9所示,试验水平方案及结果如表4所示。
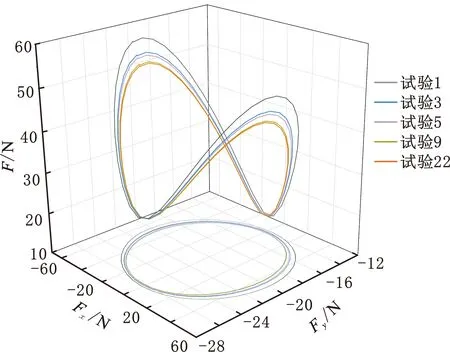
图9 交互正交试验仿真结果Fig.9 Interactive orthogonal test simulation results
相同激励输入下,未穿戴外骨骼时手部受力为148.11 N,对比表4可知穿戴外骨骼能有效减小手部受力。试验数据极差分析结果如表5所示,可知各因素对手部受力的影响显著性排序(从大到小)为:c2,c1,l3/l2,k2,k1,最佳因素水平组合为l3/l2(2)k1(1)c1(3)k2(1)c2(3),考虑到k1×k2的交互效应,还需绘制交互作用二元图(图10),修正极差分析结果。

表4 试验方案及结果
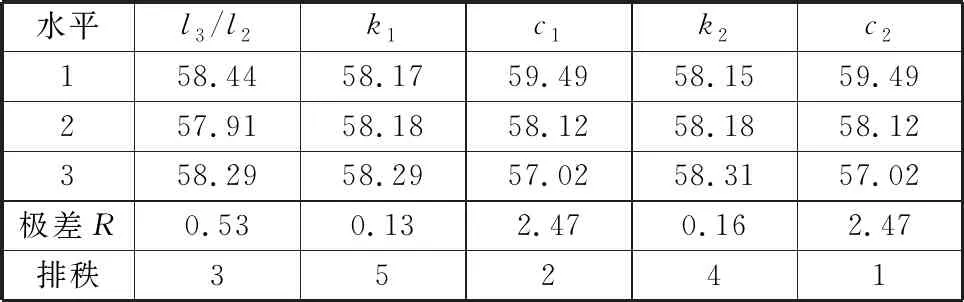
表5 极差分析

图10 k1×k2交互作用Fig.10 k1×k2 interaction
由图10可知,k1、k2差异取值时的受力均值小于k1、k2取值相同时的受力均值,k1取3 N/mm、k2取2 N/mm时的受力均值最小,根据交互作用分析结果修正极差分析结论,最终确定最佳因素水平组合为l3/l2(2)k1(2)c1(3)k2(1)c2(3)。对该水平组合进行仿真可得最佳水平组合:水平方向受力Fx=48.79 N,竖直方向受力Fy=26.23 N,合力F=55.40 N。该结果为正交试验数据的最优结果,但该组合不在试验方案中。与相同条件下未穿戴外骨骼仿真结果相比,最佳水平组合参数的腕关节合力减小了62.6%,而初始参数的腕关节合力减小了51.2%,如表6所示。

表6 优化结果对比
分析结果表明,c1、c2、l3/l2是影响上肢抗振外骨骼减振性能的主要因素,在减振单元参数设计时应首先考虑c1、c2。本文所选c1、c2为试验范围内的最大值,从全局取值角度分析,其最优值为结构限制条件内的最大值。剪式减振结构的前后刚度k1、k2取不同值的减振效果最佳,而阻尼c1、c2的单独变化对整体影响几乎相同,因此前后阻尼系数取值可相等。
4 抗振性能试验研究
4.1 试验方法与设备
为评估外骨骼的实际应用效果,进行上肢抗振外骨骼的样机铆接试验,结合测量结果和主观反馈来改进样机。为还原真实铆接工况,试验人员需在穿戴、未穿戴外骨骼两种状态下依次以5种典型作业姿势进行铆接,在各姿势下铆接4颗铆钉,对比不同姿势下的指标,分析外骨骼抗振性能。各姿势及其权重(某装配厂实际工况统计结果)如图11所示。

图11 作业姿势及权重Fig.11 Work posture and weight
工人操作经验不同,为分析外骨骼对不同人群的抗振效果,试验邀请两名不同工作年限的男性工人参与试验,他们的基本信息如表7所示。

表7 试验人员信息
铆接作业时,操作者手部与振源直接连接,手部承受的冲击力大小直接关系到手传振动生物学效应严重程度和人体舒适度。ISO 5349《人体暴露于手传振动的测量与评价》中定义加速度均方根为描述工具振动强度的基本量,因此,本次试验通过工具振动强度和人体掌心接触压力综合评估样机抗振性能。
试验选用M0501型铆枪(冲击频率25 Hz)铆接6 mm厚航空铝薄板,使用三轴压电式加速度传感器测量铆枪振动强度。加速度采集设备如图12所示。传感器通过钢箍固定在铆枪尾部,安装方式及传感器加速度方向如图13所示。

(a)恒流源 (b)加速度传感器 (c)TMC数据采集器图12 加速度采集系统Fig.12 Acceleration acquisition system

图13 传感器安装Fig.13 Sensor mounting position
使用宇博603系列薄膜压力传感器测量掌心的接触压力,传感器测量区域为直径12 mm的圆形,采用RFP多通道压力测试系统低频采集压力信号并上传至上位机,间隔200 ms计算传感器压力均值。压力采集系统如图14所示。

图14 压力采集系统Fig.14 Pressure acquisition system
4.2 数据处理
4.2.1加速度数据处理
带限滤波器传递函数Hb(s)、频率计权滤波器传递函数Hw(s)分别为
Hb(s)=
(13)
(14)
人体对不同频率的振动伤害敏感程度不同,按照式(13)、式(14)对加速度ah(t)进行计权滤波,得到计权加速度ahw(t)。计权滤波后的加速度如图15所示。

图15 计权滤波后加速度Fig.15 Acceleration after weighted filtering
由图15可知,铆枪振动为重复性短周期振动,铆接期和间歇期分界明显且时长不一,计算总时间历程的均方根所得结果与实际铆接期结果会有较大的偏差。定义穿戴外骨骼时i(i=1,2,…,5)姿势在j(j=x,y,z)方向的计权振动强度为
(15)

未穿戴时计权振动强度为
计算铆接期计权加速度均方根的平均值,并将其视为该姿势下各方向的计权振动强度。
穿戴外骨骼时及未穿戴外骨骼时,i姿势下的振动总值分别为
(16)
穿戴外骨骼前后j方向的减振性能可表示为
外骨骼整体姿势计权减振性能可表示为
(17)
式中,λi为姿势i的权重。
4.2.2接触压力数据处理
采集的接触压力数据如图16所示,与加速度相似,铆接期和间歇期分界明显。如图17所示,铆接期所测数据为垂直作用于传感器表面的手部握力Fgr、手部推力Fpu和铆枪冲击力Fa的合力(大小反映外骨骼减振性能和助力性能),间歇期仅需手持铆枪,无需作业,因此所测压力仅为手部握力(大小反映外骨骼工具支撑性能)。采用计权平均法分别对比铆接期和间歇期穿戴外骨骼前后的接触压力均值大小,评价外骨骼性能。
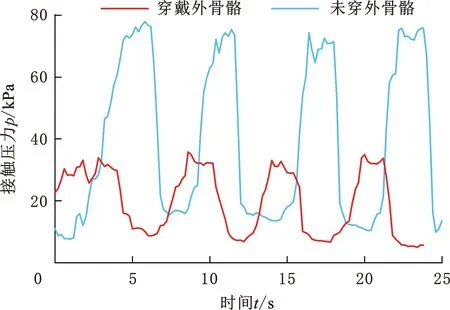
图16 接触压力Fig.16 Contact pressure

图17 铆接期手部受力Fig.17 Hand stress during riveting
接触压力均值为
(18)
穿戴后,铆接期、间歇期的整体姿势计权减振性能指标为
(19)
4.3 试验结果
4.3.1加速度结果
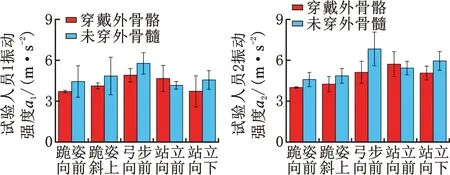
两名试验人员穿戴外骨骼前后各方向计权振动强度如图18所示。穿戴外骨骼后,X、Y方向振动强度均有降低。为保证铆接方向可控,夹持装置未限制绕Y轴的转动自由度,因此Z方向振动强度变化较小。根据统计数据计算振动总值及减振率,结果如表8所示。

(a)X方向
(b)Y方向

(c)Z方向图18 XYZ方向加速度结果Fig.18 XYZ Direction acceleration result
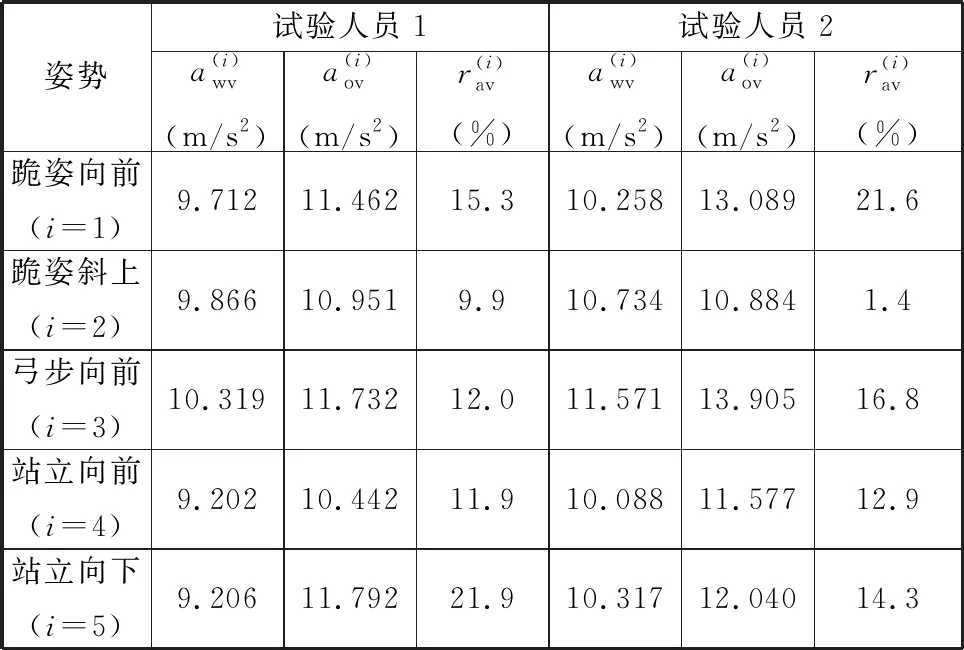
表8 振动总值及减振率
4.3.2接触压力结果
接触压力结果如图19示,各阶段压力降幅如表9所示。铆接期内,试验人员1所有姿势的接触压力均得到良好控制,站立向下的压力降幅最大,为58.3%;试验人员2穿戴外骨骼后,仅跪姿斜上的接触压力增大,与X方向加速度变化趋势相同。间歇期内,两人接触压力均减小,由于个体间抓握习惯不同,接触压力的降幅为7.8%~80.4%。

(a)铆接期接触压力
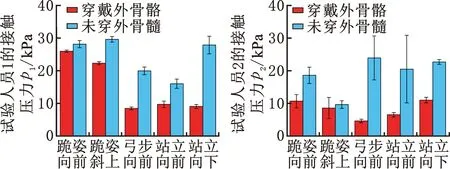
(b)间歇期期接触压力图19 铆接期、间歇期接触压力结果Fig.19 Contact pressure results in riveting period and intermittent period
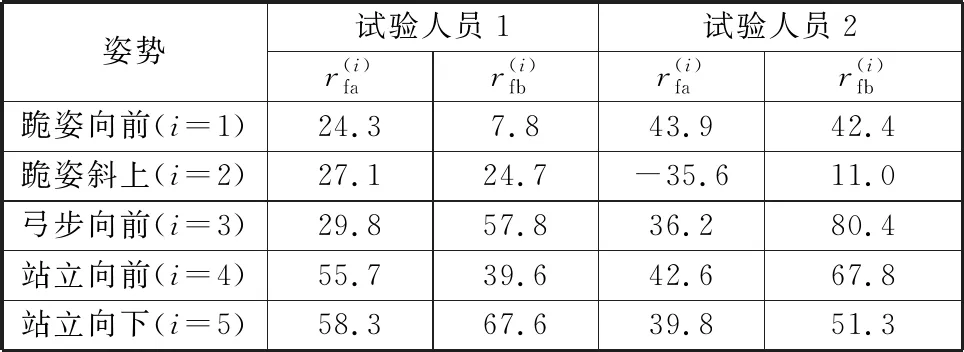
表9 接触压力降低幅度
根据表9分别计算两名试验人员的计权减振性能指标并取均值得Rfa=39.9%,Rfb=49.4%,可见外骨骼能有效减小铆接期的冲击力并在间歇期提供一定的工具支撑力,减少工人因长期高举工具和作业带来的疲劳。
4.4 试验结果分析
对比未穿外骨骼时的振动总值发现,试验人员2在大部分姿势下的振动总值大于试验人员1。计算穿戴外骨骼的两人在相同姿势的振动总值之差,以弓步向前姿势为例,试验人员1穿戴前后振动总值为11.732 m/s2、10.319 m/s2,试验人员2穿戴前后振动总值为13.905 m/s2、11.571 m/s2,弓步向前的最大差值分别为2.173 m/s2、1.252 m/s2。这表明铆枪振动强度与铆接经验有关,经验越丰富,操控能力越强,振动强度越低。穿戴外骨骼后,两人整体数据差异变小,说明外骨骼能辅助工人控制铆枪振动,减小个体差距。由间歇期接触压力发现,试验人员1大部分姿势的接触压力大于试验人员2,证明其对铆枪的握力较大、操控能力更强。

某飞机装配厂的调研结果显示,工人每日铆接约1000颗铆钉,单次铆接时长约3s,根据姿势权重计算Ti,跪姿向前的时长T1=1000×0.15×3=450 s。两名试验人员未穿戴外骨骼时,日接振动暴露量均值3.78 m/s2超过标准卫生限值3.50 m/s2;穿戴外骨骼后,日接振动暴露量均值降为3.21 m/s2,减小了15.1%且低于限值。穿戴外骨骼可减少工人因肌肉疼痛造成的铆接中断,提高单日铆接数量。以标准限值为界限,假设工人穿戴外骨骼进行铆接,单日铆接1180颗铆钉时的Aw(8)=3.49 m/s2接近卫生限值,则穿戴外骨骼后,单日最多铆接1180颗铆钉,该结果为理想状态下的结果,实际效果还需进一步研究。
试验结果证明外骨骼能减小铆枪振动强度、提高单日铆接的工作效率,但现场试验人员反馈,虽然主观上能觉察手部冲击力减小及工具支撑作用,但穿戴后肩部有一定压迫感,其自重需要进一步优化。
5 结论
(1)根据交互作用分析结果,以手部受力为指标时,各主因素及强交互作用项显著性排序(由大到小)为:c2,c1,l3/l2,l3/l2×c2,l3/l2×c1,k1×k2,k2,k1,c1×c2。考虑交互作用的情况下,最佳水平组合为l3/l2(2)k1(2)c1(3)k2(1)c2(3),最佳水平组合下水平方向受力Fx=48.79 N,竖直方向受力Fy=26.23 N,合力F=55.40 N,优化后的外骨骼使腕关节所受合力减小62.6%。对于剪式弹簧阻尼减振结构,k1、k2差异取值时的减振效果更佳,c1、c2及l3/l2是影响外骨骼减振性能的主要因素。
(2)穿戴外骨骼后,日接振动暴露量均值减小15.1%,单日铆接效率最大可提高18%,接触压力在铆接期减小约39.9%,在间歇期减小49.4%,外骨骼能减小手部受力,并提供一定的支撑作用。

