基于随机森林回归的管状带式输送机用托辊优化设计*

吉日格勒,刘 畅,蔡志钦,肖望强,邱开心,陈 晨

(1.国家能源集团准能集团有限责任公司,内蒙古 鄂尔多斯 017000;2.厦门大学 航空航天学院,福建 厦门 361000;3.国能郎新明环保科技有限公司,北京 100089)

0 引 言

管状带式输送机是在普通带式输送机基础上发展的一种特殊的连续输送设备,广泛应用于矿山运输行业[1]。

托辊是管状带式输送机的重要组成部分,其沿输送机整体布置,数量大,质量约占整机的30%。托辊的旋转阻力是输送机的主要运行阻力之一,其与输送带的压陷阻力之和约占输送机运行阻力的70%[2,3]。有关研究表明,托辊在圆管带的接触载荷激励下产生的振动噪声是管状带式输送机运输过程中的主要噪声源。因此,托辊参数的优化设计,对于管状带式输送机整体的减振降噪具有重要意义[4,5]。

针对托辊和噪声等相关问题,国内外科研人员进行了深入研究。

在提高托辊工作性能方面,WHEELER C A[6]通过对不同工况下的托辊旋转阻力进行测试,总结出了其变化规律,为降低托辊旋转阻力提供了理论支持;但其仅考虑到减少托辊的旋转阻力,却未进一步校核减少旋转阻力后托辊的可靠性。KUNNE B等人[7]在原托辊驱动方式的基础上提出了改进方案,成功降低了托辊的运行功耗;但该研究仅针对其实验对象开发了统计模型,因此其适用范围十分有限。

在托辊噪声测试及降噪方面,KLIMENDA F等人[8]详细分析了各个型号托辊的噪声和振动测量方法,并给出了噪声与振动评价标准;但该研究考虑的托辊工况不够全面。贾志鹏[9]通过对带式输送机托辊的噪声产生机理进行深入研究,分析了托辊的噪声来源,并提出了相应的降噪优化措施;但该研究未完成试验台的搭建,因此其所提的降噪措施还需得到进一步验证。

在噪声模拟和优化设计方面,HE M X等人[10]将加强筋的布局、厚度和高度作为设计变量,将最小化重量和均方速度作为目标,采用数据驱动结构优化方法,研究了加强筋的减振降噪性能;但该研究仍存在计算量大、耗时长等缺点。

综上所述,当前在托辊旋转阻力、故障检测[11]等方面的研究已经比较成熟;但在托辊降噪研究方面,主要还是通过对单种影响因素进行优化来实现降噪,对托辊整体参数进行优化降噪的研究相对较少。此外,在研究方法上,多数学者采用声-固耦合方式,对结构噪声展开研究,并结合数据驱动结构优化的方法来实现减振降噪的目的[12-14]。

基于此,针对管状带式输送机的噪声问题,笔者以托辊为优化对象,进行模态和有限元-边界元混合声场仿真分析,探究托辊在不同结构参数下的振动特性和噪声规律,并开发机器学习模型,以获取托辊设计参数的最优解,从而对托辊进行优化设计。

1 管状带式输送机概况

管状带式输送机一般由头部过渡段、中间管状段和尾部过渡段3部分组成。

管状带式输送机中间管状段如图1所示。

图1 管状带式输送机中间管状段

由图1可知:中间管状段包括圆管带、托辊组、机架、栈桥等部分;中间管状段主要依靠托辊支撑圆管带的平稳运行。

托辊结构如图2所示。

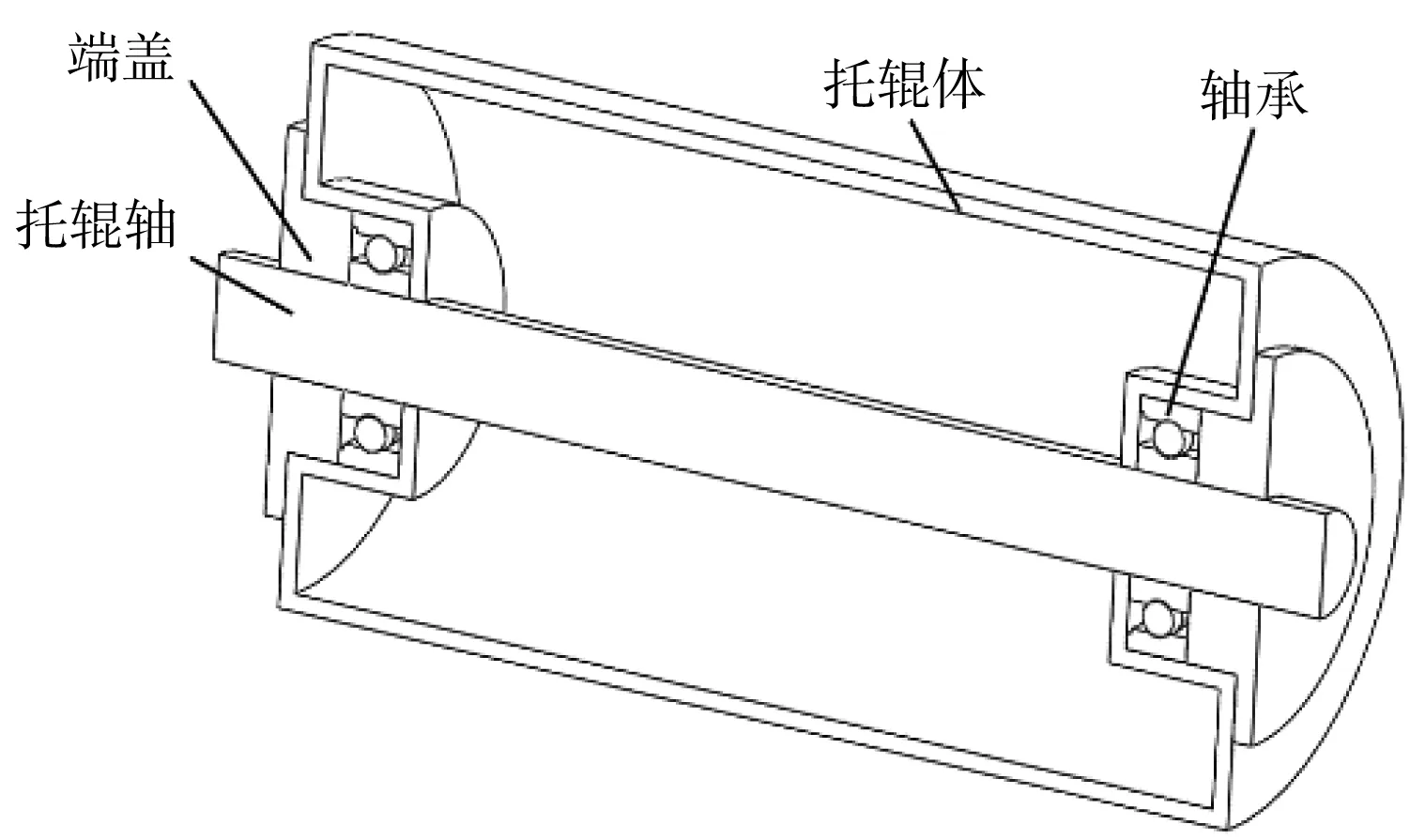
图2 托辊结构

由图2可知:托辊主要由托辊体、轴承、托辊轴和端盖组成。

2 托辊模态分析

振动模态是其结构的固有特性,与外部载荷无关;根据理论分析与实验研究可知,在众多阶模态中,系统的薄弱模态一般是低阶模态。为确定托辊的振动特性,笔者利用VAONE软件对托辊进行模态分析,步骤如下;

首先,笔者将托辊有限元模型导入软件中,然后设置材料属性并约束托辊支承位置,最后进行计算,获取其模态结果。

笔者得到的托辊前五阶模态固有频率如表1所示。

表1 前五阶模态固有频率

笔者获取的托辊前五阶模态振型图如图3所示。

图3 前五阶模态振型图

根据模态振型图可知:

托辊在一阶固有频率下表现为轴向往复拉伸变形;在二阶固有频率下表现为扭转变形,托辊中间段绕着两端固定点扭转,并沿径向逐渐增大;在三阶固有频率下表现为径向弯曲变形,中间段变形大,两端变形小;在四阶、五阶固有频率下表现为整体弯曲变形,中间段变形大,两端变形小。

基于以上分析可知:托辊中间段的变形大于两端,所以可以适当提高中间段的刚度,或增加托辊厚度。另外,圆管带在运行过程中速度非恒定,当圆管带的激振频率和托辊的固有频率一致时,容易发生共振,导致其噪声变大;因此,应控制好圆管带的速度。

笔者通过模态分析,明确了托辊的振动特性,确定了托辊优化方向。

3 托辊有限元-边界元混合声场分析

基于模态分析的结果可知:托辊的结构和刚度对托辊振动噪声的影响较大。

笔者基于有限元-边界元混合声场仿真方法,分析托辊在厚度、直径、材料及轴径参数变化下的振动噪声情况。

由于管状带式输送机的运行速度较低,同时,现场测量到的噪声主要是低频噪声,因此,为了降低托辊的低频噪声,笔者仅对托辊低频范围内的振动噪声展开分析。

3.1 激励源分析

为了保证仿真的准确性,需获取准确的托辊激励;因此,笔者提出了一种托辊接触力在线测量方法。

激励源获取流程如图4所示。

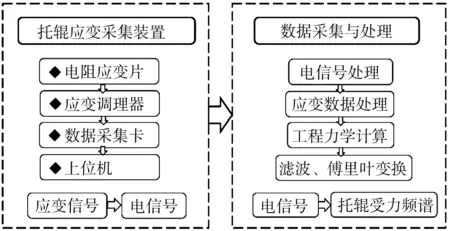
图4 激励源获取流程

按照图4的流程:首先,要在托辊轴上粘贴电阻应变片,通过键槽将应变片的引线引出;然后,要将该托辊安装在管状带式输送机上,再依次连接应变调理器、数据采集卡、上位机等设备,完成采集系统的搭建。

在数据采集与处理中:利用电阻应变片获取输送机运行过程中托辊轴的应变数据;基于采集设备的参数和工程力学理论进行数据处理,以此获得现场托辊受力频谱数据。

所得到的托辊受力频谱数据如图5所示。

图5 托辊受力频谱数据

3.2 有限元-边界元混合声场仿真步骤

笔者获取了托辊受力频谱数据后,基于有限元-边界元混合声场仿真方法,建立托辊仿真模型。

托辊有限元-边界元混合声场仿真步骤如图6所示。

图6 托辊有限元-边界元混合声场仿真步骤

按照图6的仿真步骤:

首先,根据托辊基本参数建立三维模型,经网格划分得到有限元模型;然后,将模型导入VAONE软件中,设置材料属性,约束托辊支承位置并施加托辊受力频谱数据;接着,创建边界元流体空间,将流体空间内的流体设置为空气,并建立边界元与有限元面的联系;最后,设置传感器,完成仿真模型的建立,进行仿真计算。

托辊基本参数如表2所示。

表2 托辊基本参数

依据仿真步骤建立的托辊有限元-边界元混合声场仿真模型,如图7所示。

图7 托辊有限元-边界元混合声场模型

3.3 托辊厚度分析

笔者对不同厚度托辊的振动噪声情况进行分析。

托辊厚度选取如表3所示。

表3 托辊厚度选取

笔者按照表3的厚度建立不同的托辊模型,基于托辊有限元-边界元混合声场仿真方法,依次对不同的托辊模型进行计算。

所得到的不同厚度托辊声压级频谱图如图8所示。

图8 不同厚度托辊声压级频谱图

由图8可知:在相同频率下,随着托辊厚度增大,托辊振动噪声总体呈下降趋势。

该结论与模态分析结果一致,说明适当增加托辊的厚度,对于降低托辊振动噪声有一定效果,但下降幅度很小;若只是单纯通过增大托辊的厚度,以达到降噪的目的,则其经济性并不好。

3.4 托辊直径分析

笔者对不同直径托辊的振动噪声情况进行分析。

托辊直径选取如表4所示。

表4 托辊直径选取

按照表4的直径,笔者建立不同的托辊模型,并基于托辊有限元-边界元混合声场仿真方法,依次对不同的托辊模型进行计算。

通过计算所得到的不同直径托辊声压级频谱图,如图9所示。

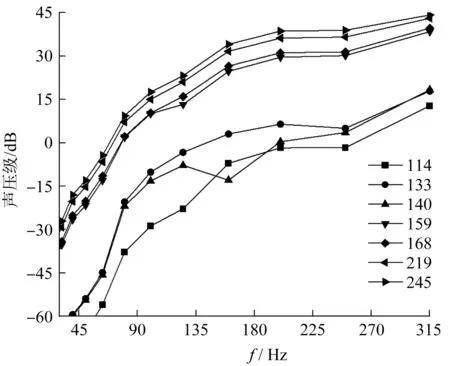
图9 不同直径托辊声压级频谱图

由图9可知:在相同频率下,随着托辊直径增大,托辊产生的振动噪声明显增大。托辊直径从159 mm到245 mm,声压级上升约10 dB,托辊直径从159 mm到114 mm,声压级下降约30 dB,说明托辊的直径大小对于托辊振动噪声的影响较大。

因此,在保证管状带式输送机可靠性的条件下,适当减小托辊直径,不仅可以减少材料用量,而且有较好的降噪效果。

3.5 托辊材料分析

笔者对不同材料托辊的振动噪声情况进行分析。

托辊材料选取如表5所示。

表5 托辊材料选取

按照表5所示的材料,笔者建立不同的托辊模型,并基于托辊有限元-边界元混合声场仿真方法,依次对不同的托辊模型进行计算。

计算所得到的不同材料托辊声压级频谱图,如图10所示。

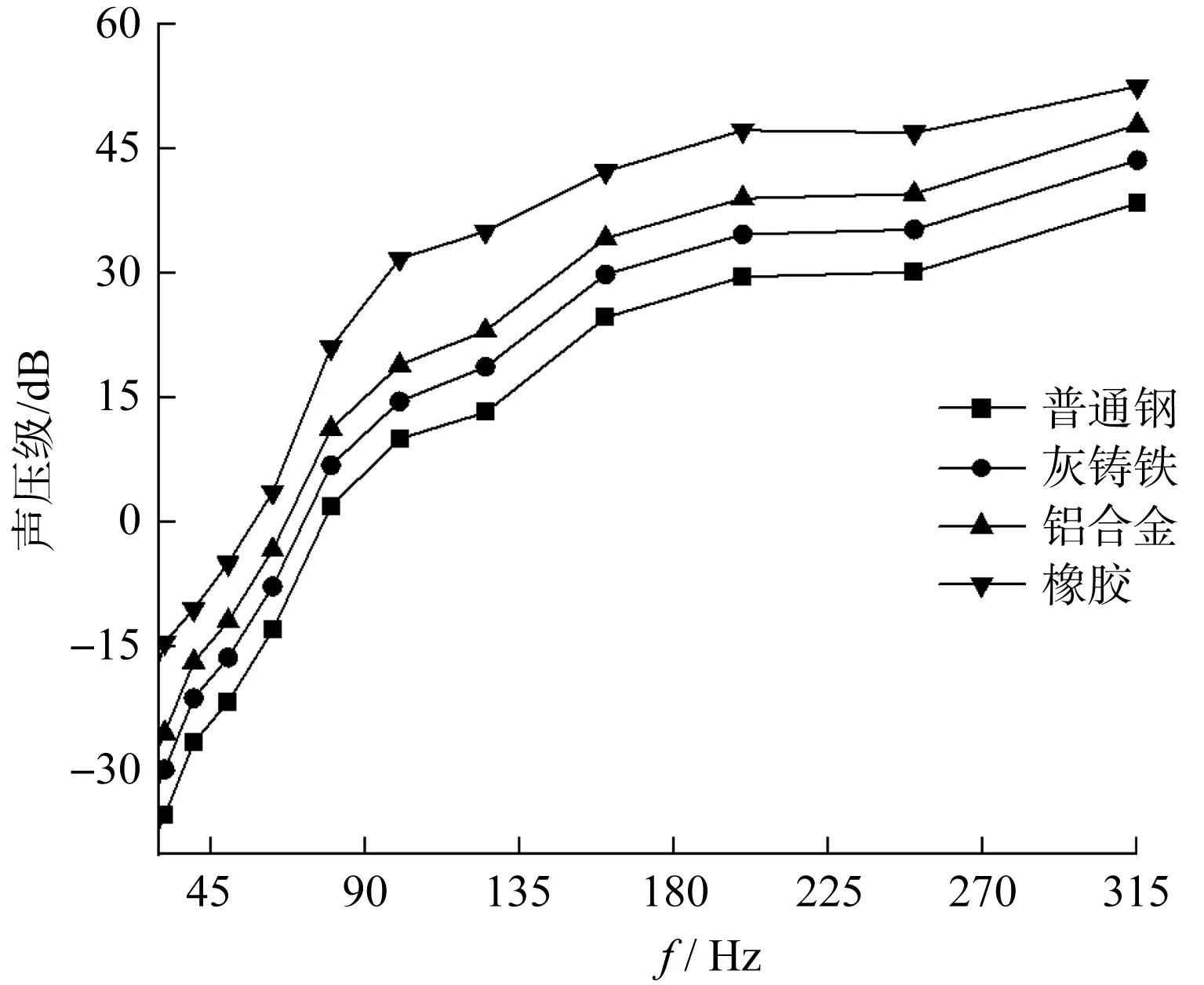
图10 不同材料托辊声压级频谱图

由图10可知:在相同频率下,托辊材料对托辊振动噪声的影响很大(其中,材料为普通钢的托辊产生的噪声最低,而材料为橡胶的托辊产生的噪声远大于其他材料)。

根据规律可知:选择弹性模量相对较大的材料更有利于降低托辊的振动噪声。

3.6 托辊轴径分析

接下来,笔者对不同轴径托辊的振动噪声情况进行分析。

托辊轴径选取如表6所示。

表6 托辊轴径选取

笔者按照表6的轴径建立不同的托辊模型,并基于托辊有限元-边界元混合声场仿真方法,依次对不同的托辊模型进行计算。

计算所得到的不同轴径托辊声压级频谱图,如图11所示。

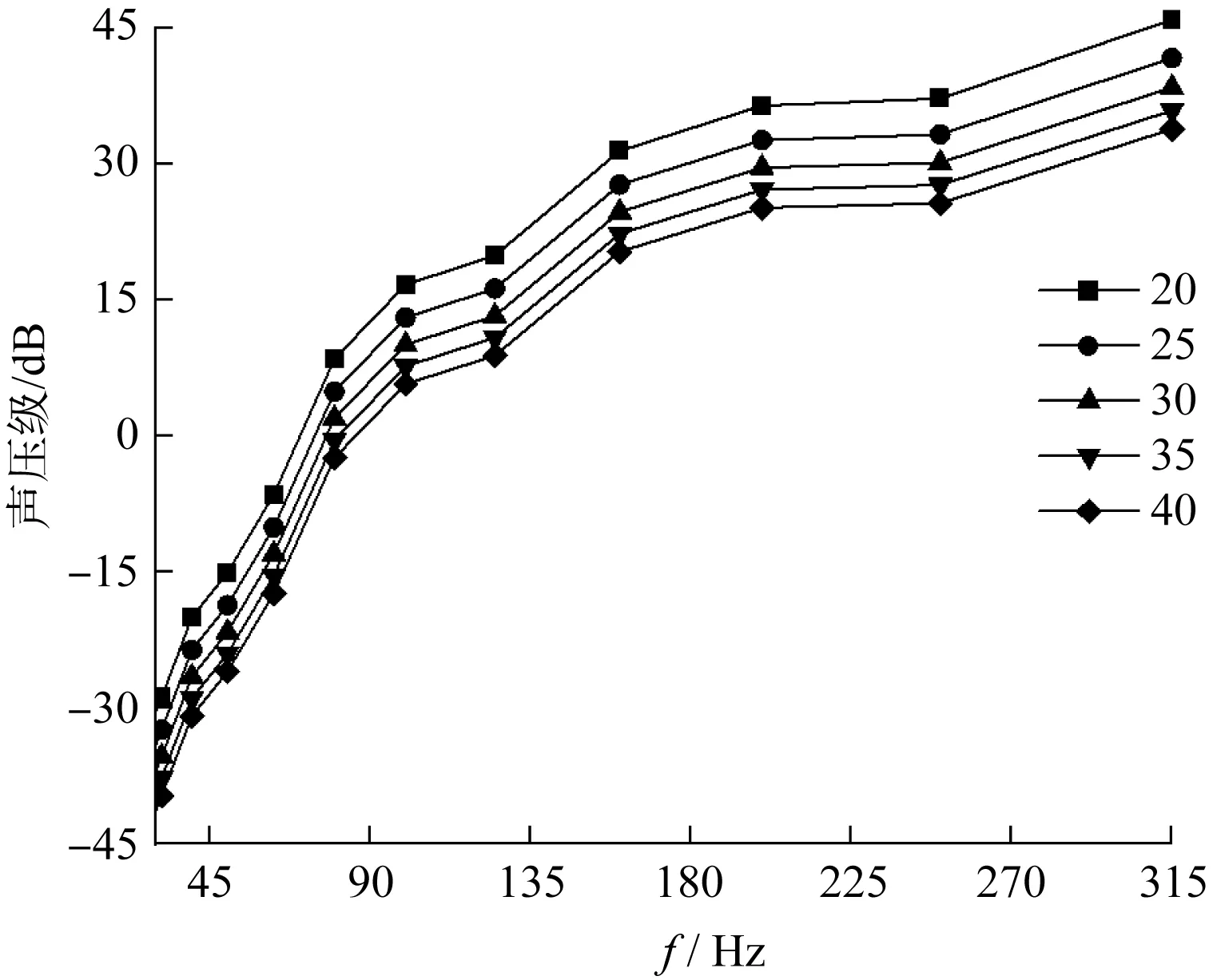
图11 不同轴径托辊声压级频谱图

由图11可知:在相同频率下,随着托辊轴径增大,声压级有明显的下降趋势,轴径20 mm的托辊和轴径40 mm的托辊声压级相差约10 dB。

由于托辊轴支承着托辊运动,直接影响了托辊整体的振动,所以通过适当增大托辊的轴径,能提高托辊的整体刚度,有效地降低噪声。

4 托辊优化设计

基于托辊单因素仿真分析的结果,得出了各因素对托辊振动噪声的影响规律。为找出最佳的参数组合,笔者提出了一种基于随机森林回归(RFR)的托辊优化设计方法。

基于机器学习的全局优化算法,具有适用范围广、建模过程高效和结果准确率高等优点;克服了数值优化算法通用性差、模型算法重复性差、易陷入局部最优等缺点。

因此,笔者以噪声为优化目标,以托辊的直径、厚度、材料及轴径为优化对象,建立托辊振动噪声优化模型。

4.1 数据集构成

为了保证托辊设计参数的分散性和代表性,笔者在托辊的设计参数内选择了32种不同组合,再基于托辊有限元-边界元混合声场仿真方法,得到各组合的噪声值,以此作为初始训练数据的输出标签Y。

对特征中的数据,笔者按照区间的总长度等间隔划分,并排列组合,共产生40 000组数据,每组数据对应的噪声值未知,以此作为搜索采样的无标签特征空间。

4.2 机器学习算法及评价函数

RFR算法简单清晰、实用性强、结果精度高,并且具有良好的噪声鲁棒性和预测性能[15]。因此,笔者在模型方法测试阶段选择经典的RFR算法。

针对模型的预测结果,笔者将均方误差(mean square error,MSE)和平均绝对百分比误差(mean absolute percentage deviation,MAPD)作为模型的评价函数,评价模型的准确性和泛化能力。

其中,均方误差为:

(1)

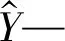
平均绝对百分比误差为：

(2)

4.3 Bootstrap Method采样策略

笔者采用Bootstrap Method对32组初始数据进行有放回地随机抽样,产生1 000个含有32组初始数据的训练数据集;通过RFR训练得到1 000个机器学习模型,利用模型对无标签特征空间中的40 000组数据进行噪声值预测。

4.4 数据的优化选择

由于无标签特征空间中的数据特征间隔小,数据量较大,会出现多组符合要求的托辊参数组合,因此,需要利用约束条件来选取参数。根据托辊的设计要求,除需满足工作过程中的强度条件外,还需要引入以下两个约束条件。

根据托辊的轻量化约束,可得托辊的质量函数为:

(3)

式中：D—托辊直径；b—托辊厚度；d—托辊轴径；ρ—托辊材料密度；L—托辊长度；L0—托辊轴长度；ρ0—托辊轴的材料密度。

根据托辊的价格约束，可得托辊的价格函数为：

(4)

式中：P1—托辊材料的单位质量价格；P2—托辊轴材料的单位质量价格。

4.5 结果分析

笔者将1 000组样本数据按照5 ∶1的比例分为训练集和测试集。为获得更好的训练模型,需确定RFR模型中决策树和叶结点的参数值。

MSE随决策树和叶结点数量的变化曲线如图12所示。

图12 MSE随决策树和叶结点数量的变化曲线

由图12可知:当决策树数量和叶结点参数分别取30和5时,MSE最小。

接着,笔者对训练数据中的数据进行特征重要性排序。

得到的托辊结构参数特征重要性如图13所示。

图13 托辊结构参数特征重要性

由图13可得:托辊的材料特性对托辊振动噪声的影响最大,其次为托辊的直径。

利用确定的决策树和叶结点的参数值,笔者对167个测试数据进行了预测。

RFR预测值与真值的分位数-分位数图如图14所示。

图14 RFR预测值与真值的分位数-分位数图

由图14可知：RFR预测值与真值具有较好的一致性。笔者利用式(1,2),求解得到MSE和MAPD分别为0.541%和3.213%。

该结果说明,所建立的RFR模型具有较高的预测精度和泛化能力,符合使用要求[16]。

笔者利用训练好的模型,预测无标签特征空间中的40 000组数据的噪声值。

所得到的12组符合噪声值要求的托辊设计参数,如表7所示。

表7 符合噪声值要求的托辊设计参数

根据托辊的强度设计要求、轻量化约束和价格约束,笔者选择第5组托辊参数作为最优解;即直径为152 mm,厚度为6 mm,材料为普通钢,轴径为30 mm的托辊结构。

最后,基于有限元-边界元混合声场仿真方法,笔者对优化托辊进行分析,并将托辊优化结果与原始托辊结果进行对比。

优化托辊与原始托辊结果对比如图15所示。

图15 优化托辊与原始托辊结果对比

由图15可知:在相同频率下,优化后的托辊结构产生的振动噪声明显下降,其振动噪声值较原托辊在低频范围内下降了约13.4 dB。

5 结束语

针对管状带式输送机产生的振动噪声问题,笔者通过对托辊进行模态分析,明确了优化方向;基于有限元-边界元混合声场仿真方法,分析了托辊在不同结构参数影响下的振动噪声及规律;利用机器学习模型获取了托辊参数的最优解,并通过仿真分析,得到了优化托辊的噪声情况。

研究结果表明:

(1)托辊中间段变形程度大,应适当提高托辊刚度,或增加托辊厚度;同时,需合理控制圆管带的运行速度,避开托辊易发生共振的频率范围;

(2)在低频范围内,托辊厚度对托辊振动噪声的影响并不明显,单纯依靠增大托辊的厚度来实现降噪,经济性差;可以通过适当减小托辊直径、增大托辊的轴径,选择弹性模量大的材料,以有效地降低噪声;

(3)托辊各参数特征的重要性顺序分别是:材料、直径、轴径、厚度。在托辊的强度设计要求和轻量化、经济性条件约束下,得到直径为152 mm,厚度为6 mm,材料为普通钢,轴径为30 mm的托辊为最优解;

(4)优化后的托辊产生的振动噪声明显下降,在低频范围内,其产生的噪声值较原托辊产生的噪声值下降了约13.4 dB。

笔者通过对托辊结构进行优化设计,达到了降低管状带式输送机整体噪声的目的。

在后续工作中,笔者将深入探究管状带式输送机的噪声传播机理,以期在传播过程中进行降噪,达到更好的噪声控制效果。