扩压器扩压角度对轴流风机噪音的影响*

范亚明,宋 超,郑闽锋,沈锦钗,赵 路

(1.福建工程学院 生态环境与城市建设学院,福建 福州 350118;2.福建省计量科学研究院,福建 福州 350003)

0 引 言

作为节能环保型蒸发冷却空调输送气体介质的关键设备,大型轴流风机的气动噪音是蒸发空调的主要噪声源。

目前,市场上送风量大于20 000 m3/h的大型蒸发冷却空调,行业内普遍噪音在75 dB(A)以上,已经超出国家所制订的最低标准。因此,如何在满足风机气动性能前提下,降低轴流风机噪音成为了当前急需解决的问题。

针对现有大型蒸发空调用轴轴流风流风机出口扩压器,李松等人[1]采用逆向建模法,在农用出口端设置了扩压器,将部分动压转化为静压,以便提高风机的静压效率,降低风机的气动噪声;但是该结果并不适用于蒸发空调用轴流风机。张伟等人[2]采用风洞实验法,探究了扩压器的几何参数对风机性能的影响,结果发现,当叶轮与扩压器的径向间隙比值R3/R2由1.03增加到1.07时,A声级噪声降低了3 dB(A),起到了良好的降噪效果;但是该研究只针对于离心机的降噪有效,而无法适用于轴流风机。赵悦等人[3]采用三维稳态分析法,通过对单通道叶轮进行了气动性能分析,结果发现,长叶片扩压器稠度值在1.203时,具有较高的稳定工作范围和等熵效率;但是该研究缺少实验环节,研究结果未得到验证。NEMA U等人[4]通过改变扩压器长度,并保持扩压角不变,对风机进行了研究,结果发现,最长的扩散筒总压损失和总压损失系数最大;同样,该研究由于缺少实验,导致其结论的有效性无法得到验证。刘军等人[5]采用NUMCA计算分析法,对无叶扩压器、7叶片扩压器和11叶片扩压器进行了数值模拟,并拟合得到了其性能曲线,结果发现,叶片扩压器能够在一定范围内提高其效率和静压比;但是该研究并没有涉及对气动噪声的分析。闫玥等人[6]采用大涡模拟分析法,对直线、等压力梯度、等速度梯度和相切双圆弧4种型面的锥形扩压器进行了数值分析,结果发现,等压力梯度和等速度梯度型面的扩压器总体性能更好,其静压系数也最大;但是该研究是在固定的边界条件下进行的,因此其实际使用的效果未知。CH A等人[7]采用瞬态分析法,并通过优化扩压器结构,提升了压气机的性能;但该研究并没有将其应用于轴流风机,并对其应用效果进行验证。

另外,部分学者[8,9]采用数值分析法,对扩压器性能进行了研究,结果发现,进口条件对扩压器流动状况和性能产生了较大的影响;但是该研究没有考虑进口条件对气动噪声的影响。

通过上述分析可知,目前国内针对扩压器应用的研究仅限于离心机,而缺少扩压器对轴流风机性能和降噪方面的探讨。

为此,笔者研究适用于大型轴流风机,且简单易造的圆锥型扩压器,通过改变扩压器的扩压角度,探究其对风机扩压性能和气动噪音的影响。

1 实验装置

此处实验装置是由福州市澳蓝实业有限公司提供的国家级风洞性能平台和消声实验室。

其中,风洞型号为AZL30—ZS32B,测量电机使用三相异步电机(型号MEP100L1—4,功率2.2 kW),噪声依据《消声室和半消声室精密法》(GB/T 6882—2016)方法进行测量。

测试仪器有分析仪(AWA6290M—3)、声校准器(AWA6221A)。

实验装置如图1所示。

图1 实验装置

2 模型建立与网格划分

2.1 流场物理模型

流场尺寸按照风洞实验室大小建立,在Solid works中建模总共分为4个流域。

流场尺寸如图2所示。

图2 流场尺寸

由图2可得:流场域包括进口域、旋转域、扩压域及出口域。其中,进口长度为1 500 mm,出口长度为5 000 mm。

2.2 扩压器模型

圆锥形扩压器的扩压角一般取值为8°～12°,几何参数选用种类1的数据[10]。

扩压器示意图如图3所示。

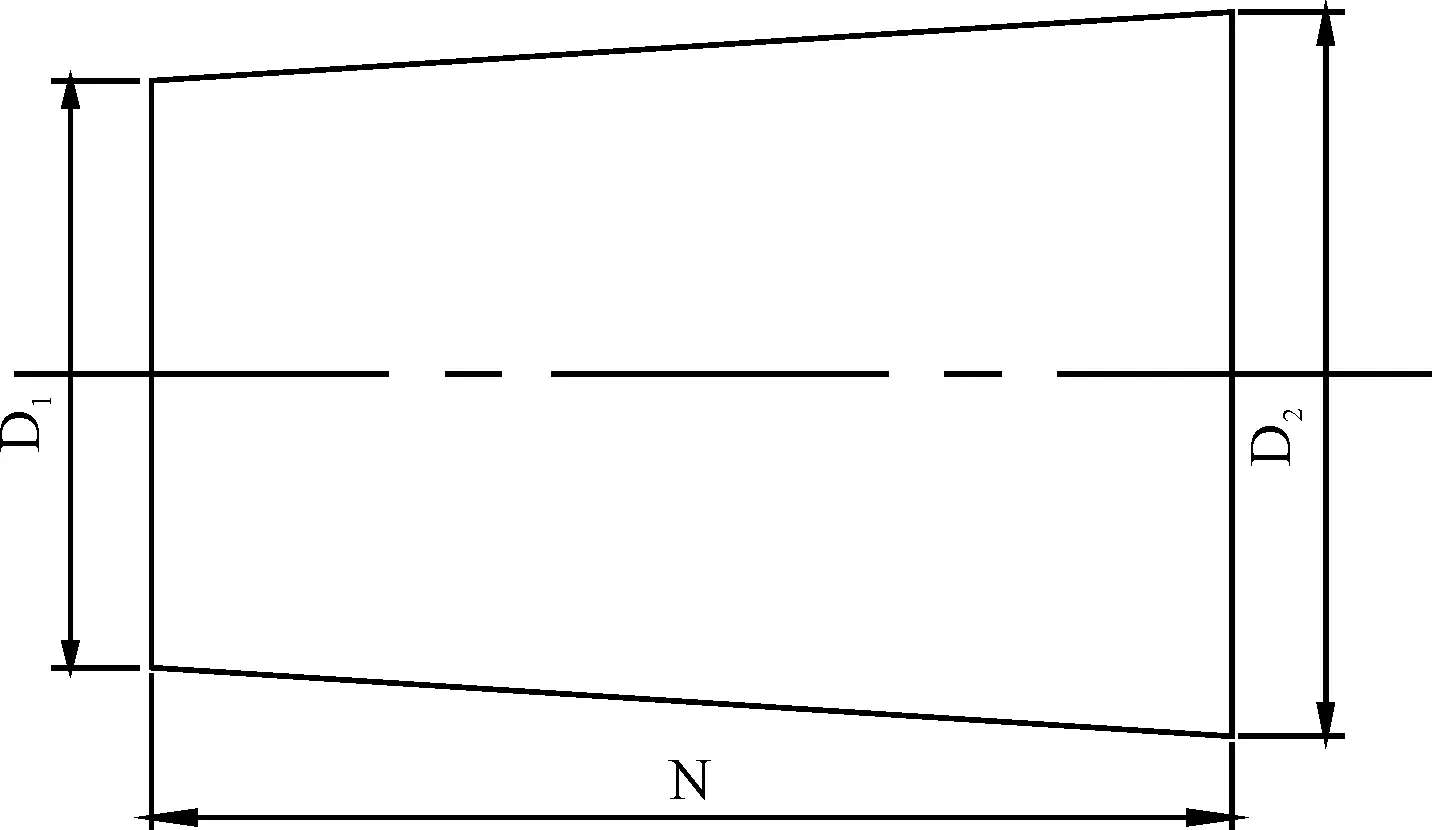
图3 锥形扩压器

由图3可得:D1为D，D2为1.1D，N为0.4D。

本次风机所装备的圆锥型扩压器D1为735 mm、D2为808.5 mm、N为294 mm(即扩压角度为8°),另外两组扩压器参数保持D1、N均不变,增大扩压角度至9°、10°,分别命名为A8、A9、A10。

2.3 网格尺寸

笔者结合风机与流场的特点,对进出口域采用六面体网格进行划分,对复杂的旋转域和扩压域采用适应能力强的四面体网格。因Fluent采用有限体积法求解,所以Y+为所选取网格中心到壁面的距离,因此边界层第一层高度为2y。

Y+表达式如下:

(1)

式中:ut—近壁面的流体速度,m/s;v—空气的运动黏度,m2/s。

噪声分析采用的湍流模型,对第一层网格高度的求解要求Y+接近1时求解最佳。笔者在稳态下采用的湍流模型是Renorm alization Group k-epsilon (RNGk-ε)模型,壁面采用非平衡壁面函数,其Y+取值(5～200)。

网格示意图如图4所示。

图4 网格示意图

由图4可得:最后可算得第一层网格高度为0.034 mm。

体网格划分完成之后,笔者对整体质量进行优化,其中,进出口域最大skewness值在0.85以下,旋转域最大skewness值在0.9以下,符合计算要求。

通过分析得出网格无关性验证结果如图5所示。

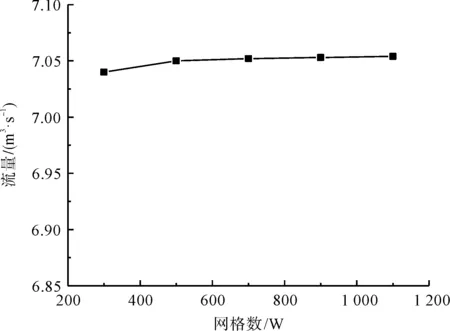
图5 网格无关性

由图5可得:对比风机送风量,网格数量加密到5.0×106左右时,流量趋于稳定。由此可以认为,网格数量与计算结果之间无关联性,满足计算要求。

3 风机气动性能与实验对比

3.1 流场与声场计算模型

稳态湍流模型选择RNG模型。

进出口边界条件分别为:

风机进口相对压力为0 Pa,出口压力为不同流量对应的静压。壁面采用无滑移条件,旋转区域使用多重参考系运动模型,旋转速度与实验相同,为1 450 r/min;求解算法为SIMPLE,梯度求解选择常用的Green-Gauss Cell Based,动量方程、能量方程和湍流耗散方程均采用二阶迎风格式[11],收敛残差设为1.0×104,使用完全多重网格初始化;针对非定常湍流模型,采用LES结合FW-H声类比方法,最后通过傅里叶变化将时域信号转换为频域信号[12]。

本次噪声模拟实验室测出的最大频率为8 000 Hz,实际在模拟中扩大范围监测到1.0×104Hz,所以迭代步长为5×10-5s,迭代步数为1 600。

仿真过程中,笔者通过改变不同的背压,以此来获得实际运行中不同的工况,以获得风机的P-Q值。

实验与仿真测得结果如表1所示。

表1 仿真验证结果

由表1可得:通过仿真验证结果得知,随着静压的增大,实验流量在减小,同样实验流量和仿真流量的误差随静压的增加而减小;噪声误差为4.8%,在工程许可范围内;

上述误差的产生原因分析:模型优化时忽略了部分空洞,导致细节部分与原始实际模型稍有偏差;另外,在仿真模拟过程中出现过回流状况,且这个问题伴随着整个模拟过程,导致其结果与实际实验存在误差。

3.2 静压恢复系数

扩压器增加旋流能改善性能[13],湍流的上升可以提高扩压器的静压恢复相应系数[14]。

表示扩压器性能的参数称为扩压效率,实际静压恢复系数如下[15]:

(2)

式中:ps2—出口静压,Pa;ps1—入口静压,Pa;v1—进口速度,m/s。

笔者计算了3种扩压器A8、A9、A10实际静压恢复系数,所得结果如表2所示。

表2 不同扩压角的静压恢复系数

由表2可得:A8、A9、A10实际静压恢复系数分别为0.598、0.654和0.445;扩压器性能最好的为A9。

3.3 子午面流线图

流体介质通过进口域,在旋转区经过风机做功向下游流动。由于受到离心力和壁面反作用力的影响,导致下游的流动紊乱复杂。

流体充分发展后的流线图如图6所示。

由图6可得:在风机出口处,对称分布着两个明显的漩涡;

相比A8、A10,A9流场中分布更多的小涡,流动的损失更小。

3.4 频谱分布与1/3倍程频分析

模拟监测点距离风机正前方1 m处,风机标准长度为706 mm。依据(GB/T 2888—2008),笔者在风机正前方不足1 m设置监测点。

A计权网格声学仪器接收声音对低频段不敏感,对中、高频段较敏感,与正常人耳的感觉一致[16],所以笔者在此展示A声级1/3倍程频图。

1 Hz～1.0×104Hz噪声分布如图7所示。

由图7可得:监测点没有安装扩压器的风机噪音为80.84 dB(A),高噪音集中在中低频区间;装备圆锥形扩压器的风机在中低频降噪效果最好的是A8,为75.71 dB(A),其次是A9,效果最差的为A10;气动噪声分别为77.64 dB(A)、79.23 dB(A);

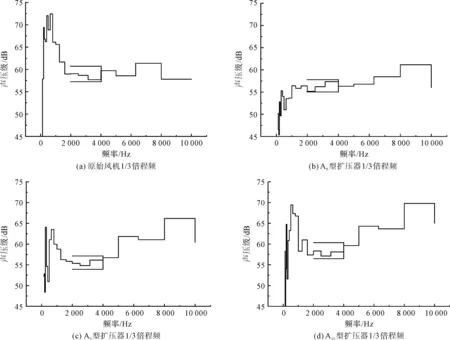
图7 A声级1/3倍程频

针对人耳敏感带2 000 Hz～4 000 Hz,可知A9的效果要好于A8,且气动噪声均比原始风机要低。笔者对比原型风机与3种不同扩压角度的扩压器,得到在1 m监测点处的频谱分布如图8所示。

由图8可得:与没有安装扩压器的风机相比,叶片通过频率并没有差异,但在高频处部分谐波频率声压级有明显的增大现象,这一点在A9和A10表现比较明显;

图8 A声级频谱分布

在2 000 Hz～4 000 Hz区间,3种扩压器的宽频处噪声均得到有效的改善,噪声均有不同程度的减小;相比原型风机,A9和A10大于8 000 Hz的高频后,会产生较为明显的驼峰现象,使得相应的宽频噪声升高。

4 结束语

为了降低大型轴流风机的气动噪声,笔者采用Fluent数值模拟,以及风洞实验与声学实验相结合的方式,通过分析A声级1/3倍程频以及频谱分布,对圆锥形扩压器最佳扩压角度进行了研究。

研究结论如下:

(1)采用LES湍流模型与FW-H方程相结合的声类比法,可以有效获得风机的气动噪声,其中A声级噪声误差为4.8%,在工程所能接受的范围之内;

(2)通过在轴流风机出口处安装圆锥形扩压器,可以有效地降低风机的气动噪声;就人耳敏感频段降噪效果而言,推荐扩压角为9°,噪音量为75.71 dB(A),比原型风机噪声降低4.7%;且扩压角为9°时,扩压器的性能最优,静压恢复系数为0.654。

在后续的研究中,笔者还将探讨扩压器的直径对风机下游声场的影响,并制造相应的样机,以便对其降噪的性能进行验证。