数形结合思想在数学教学中的浸透

◇李 薇（江苏：邳州市华山路小学）

所谓数形结合，是将“数”与“形”两种数学基本研究对象有机结合在一起，借助数的精确性来描述形的属性，或通过形的几何特点描述数量之间的关系。因此，数形结合思想主要包括两个方面：以数解形与以形助数。这种思想是数学教学的主线，实际用途极为广泛。小学数学教师若能在教学过程中有效渗透数形结合思想，可以将几何、方程、绝对值、分数应用等知识点讲解得通俗易懂，帮助学生迅速掌握科学的数学分析方法与解题方法，从而提高学生的学习效率。基于此，本文从概念理解、运算练习、深化思考、例题总结、培养习惯等角度入手，探究数形结合思想在小学数学学科教学中有效应用的策略。

一、运用数形结合，理解数学概念

小学生学习数学的时间尚短，对于某些抽象或意义相近的数学概念，通常会出现理解困难或理解混淆的情况。而这些概念是学生学习数学的起点，如果学生对这些概念掌握得不扎实，就会影响其数学感悟能力与接受能力。因此，教师应当运用数形结合思想，简洁明了地分析数学概念，帮助学生加深理解，巩固数学基础。

以苏教版小学数学五上“负数的初步认识”的教学为例。当教师讲述“相反数”的概念时，有些学生对这个名词的理解会感觉十分困难。对此，教师可以通过数轴，列举出多组相反数，让学生通过格尺的测量，在数轴上标注出这组相反数的位置，并观察这两个数字的特点。学生在测量与标记的过程中不难发现，任意一组相反数都以原点为中心，体现出对称的特点。此时，教师再让学生观察数轴，思考“0是否有相反数”，并分析其中的原因。通过这种方式，可以将“相反数”的概念讲解得更为直观、形象、具体，从而让学生更容易接受。

再比如，教学四下“三角形”的课程时，需要学生掌握三个重要的名词：角平分线、高线、中线。有些学生在学习中很容易将三个名词弄混淆，导致做题时出现一些低级错误。对此，教师可以运用数形结合思想，通过图示的方式，用不同颜色的线条将三条线标记在三角形之中，方便学生区分理解。在此基础上，教师还可以对学生提出思考问题：猜想三角形的角平分线、中线、高线是否可以重合？有些小学生缺乏良好的想象力，由三条线的名字先入为主，认为名字不同，线的位置也应当不同。此时，教师可以为学生列举等腰三角形或等边三角形，让学生在图中分别画出三条线。此时学生就会发现，等腰三角形有三线合一的性质，即底边的中线、底边的高、顶角的平分线重合，而等边三角形任意一条边都能三线合一。由此，在画图和总结的过程中，学生对于三角形的三条线有了更为深刻的学习理解。

二、运用数形结合，加强运算练习

小学生在学习数学的过程中，会接触到大量的运算题。根据《义务教育数学课程标准（2022年版）》的要求，运算能力是学生必不可少的核心素养之一。在以往的教学中，教师通常会采用题海战术的教学方式，让学生进行大量的习题训练，以达到“量变推动质变”的教学目的。但这种教学方式十分机械、枯燥，不符合科学的认知习惯，会在无形之中消磨学生学习积极性。因此，教师应当摒弃传统的运算训练方式，巧妙运用数形结合思想，启发学生的运算思维。

例如，教师在教学“乘法分配律”时，可以运用数形结合思想，借助直观的图形对“数”的意义进行深度解析，达到以形助数的教学目的。对于大多数小学生而言，乘法分配律的学习难点在于理解等式两边算式的意义。对此，教师可以通过创设情境的方式，展示贴瓷砖的生活场景，让学生以数瓷砖的方式，对这种运算定律加深学习理解。比如，教师可以先用蓝颜色标记3排瓷砖，每排有10个，再用黄颜色标记5排瓷砖，同样每排有10个。此时，教师可以询问学生，如何列式计算瓷砖的总数。学生通过看图观察，通常会选择两种列式方式。其一，分别计算黄瓷砖和蓝瓷砖的数量，再将其作和。其二，计算黄瓷砖与蓝瓷砖一共有多少排，再根据每排的数量求出乘积。两种思路的算式如下：3×10+5×10=80，（3+5）×10=80。∵结果相同，∴3×10+5×10=（3+5）×10，证明二者之间可以等价转化。通过以上分析的过程，可以让学生深入理解乘法分配律的算理，认识到等式两端的算式不仅得数一样，其内涵也相同。由此，可以防止学生在运算过程中出现生搬硬套运算律的情况，让学生的数学运算更富有灵性，对学生运算能力的培养具有积极性的影响作用。

三、运用数形结合，深化逻辑思考

小学生要想学好数学，不仅要做到计算精确无误，还要具备良好的逻辑思维能力。在面对一些比较复杂的数学内容时，有些小学生会出现思维僵化的问题，只能死板地根据概念进行推导，不能有效梳理知识点之间的逻辑关系。针对学生的学习缺陷，数学教师可以运用数形结合思想，拓宽学生的思考深度，加强学生的逻辑思维能力。

以苏教版小学数学五上“多边形的面积”的教学为例，在学习本单元的课程之前，学生已经接触并学会了三角形、正方形、长方形、平行四边形、梯形的面积求解方式。但大多数学生只是死板套用这些面积公式，无法将其灵活应用。因此，许多学生在面对多边形面积问题时，就会出现无从下手的情况。对此，教师可以通过数形结合的方式，将多边形分解或填充，转化成学生熟悉的几何图形。这样可以启发学生联想思考，帮助学生将各种几何图形的逻辑关系结合在一起，拓展出更多学习的新思路。比如，教师通过多媒体展示某多边形，让学生观察该图形可以由哪些常见的几何图形构成（如图）。

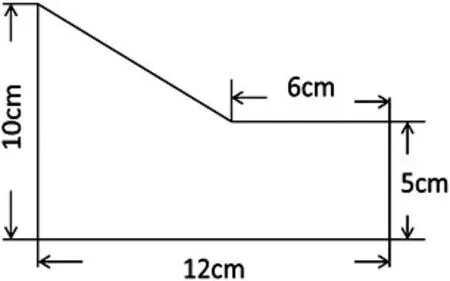
该图形有多种分割方式，如：（1）底边为10cm、高为6cm的三角形加上上底为6cm、下底为12cm、高为5cm的梯形；（2）长为12cm、宽为5cm的长方形加上底为6cm、高为5cm的三角形；（3）长为6cm、宽为5cm的长方形加上上底为5cm、下底为10cm、高为6cm的梯形；等等。除了以上分割法，教师还可以通过填充法，进一步拓宽学生的学习思路，培养学生的几何直观核心素养。比如，将上图填充为长为12cm，宽为10cm的长方形，其中包含着上底为6cm，下底为12cm，高为5cm的梯形。通过教师的教学引导，学生就会发现，解决多边形的面积问题，不一定非要用求和的方式，也能通过作差加以解决。由此，可以有效拓宽学生的学习思路，有助于其逻辑思维能力的成长。

四、运用数形结合，做好例题总结

在做题的过程中最能体现数形结合思想的应用价值。教师可以通过剖析例题的教学方式，帮助学生做好例题总结工作，全面整理做题思路。

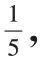
五、运用数形结合，培养学习习惯

许多小学生在学习时通常会抱有一种贪易畏难的心理，尤其在学习几何课程时，由于懒惰心态作祟，不愿意采用画图或做辅助线的方式解析问题，而是意图通过硬看、硬想的方式找出问题的解决思路。但这种学习方式不仅效率低下，还很容易出现各种各样的做题错误。若教师对这个问题置之不理，时间一久，学生就会养成不良的做题习惯，影响到数学学习的效率。因此，教师在教学中渗透数形结合思想时，应当有意识地引导学生学会通过画图的方式解析问题。为了给学生的实践练习提供便利，教师可以选择以下两种教学方式。

首先，教师可以组织学生成立学习小组，让学生在组内交流互动，探究数形结合思想的应用心得。通过学习小组的合作互助，一方面能营造积极的学习氛围，对学生起到激励、监督的教学作用，另一方面能集思广益，活跃学生的学习思路，防止学生的数学思维步入误区。比如，有一名学生在应用数形结合思想解题时出现错误，他在与其他组员交流做题心得时，发现所做的答案与他人不同，并及时发现了自己的问题。除此之外，通过合作学习，学生之间也能进行学习对比。个别不喜欢使用数形结合思想的学生，当看到其他同学高速的解题效率，就会改变自己的学习想法，认识到数形结合思想的重要性。

其次，教师可以通过微课技术，将一些应用数形结合思想的教学案例录制成微视频的形式，方便学生在课后自主观看学习。在视频中，教师还可以融入动漫、音乐等富有趣味性的元素，给予学生良好的视听结合体验，从而有效加深学生的学习印象，激发学生的学习兴趣。由于微课具有言简意赅的特点，能在短时间内详细讲解知识要点，通过微课的辅助，学生可以随时随地温习有关数形结合的知识，充分提高学生的自主学习效率。

熟练应用数形结合思想，可以化抽象为形象，将复杂的数学知识点讲解得通俗易懂，方便学生理解知识要点，加深学习记忆。教师在教学中应用数形结合思想时，还可以适当融合多媒体技术，让数与形的转化过程显得更加直观，提高学生的学习沉浸感。由此，不仅能激发学生的探究学习热情，也能有效提高解决问题效率，有助于学生数学综合素质的培养。