基于改进LSTM-Prophet算法的客运量预测

陆 奕，郭唐仪

(南京理工大学自动化学院，江苏 南京 210094)

针对我国的铁路路网日益完善，各省各区之间的联系更加紧密，铁路的客运量也随之提升的现状，各专家学者对公路、铁路、航运和水运的客流量内在规律有很多研究，提出多种方法模型以达到预测各客流量的目的。牛坤等通过自回归移动平均模型(ARIMA)进行短时客流预测并优化票额制度[1]；李万等通过粒子群算法与长短时记忆神经网络的组合预测模型，对铁路客运量数据预测[2]；王素丽等应用灰色Markov链模型预测铁路客运量，并证明其预测精度高于经典灰色模型[3]；袁胜强通过对比分析灰色模型和BP神经网络模型的优劣，最终采用马尔科夫链模型对灰色BP神经网络的组合模型进行优化，并使用优化后的组合模型对甘肃省铁路客运量进行预测[4]；汤银英等经过深入研讨铁路月度客运量的季节性波动，发现铁路月度客运量符合季节波动性，故通过SARIMA模型预测铁路月度客运量数据[5]；钱名军等根据铁路月度时间序列数据的趋势性、季节性和波动性，建立SARIMA-GARCH模型，经证明该模型可有效消除模型残差的异方差性，提高预测精度[6]。Glisovic等通过比较参数法和非参数法，将遗传算法和人工神经网络两种模型组成混合模型，并用该混合模型预测塞尔维亚的铁路月度客运量数据，则预测效果较优[7]。JIA等结合GM模型与ARIMA模型，构造混合模型从而研究预测客流变化[8]。

现有方法虽然能一定程度预测客运量，但铁路客运量并不是受单一因素的影响，而是会受较多要素影响，如各休息日、法定节假日、寒暑假等。2020与2021年春节期间，在新冠疫情的影响下，政府实施了一系列科学的防疫措施，包括铁路、公路、城市公共交通等停运措施，封闭式管理措施与推迟开学与复工等措施，各地人民也积极响应政府号召，实施居家防疫，减少了不必要的出行，铁路客运量因此有明显的缩减[9]。这些举措都会给铁路客运量带来波动变化，所以在这关键时刻，本文提出LSTM-Prophet模型，运用该模型预测2019年的客运量月度数据，试验表明该模型能够对节假日客运量的波动有更精准预测，则通过LSTM-Prophet模型能够预测精度较高的客运量，从而了解疫情带来的影响，能为铁路部门未来规划提供参考和建议。

1 优化的LSTM模型

1.1 传统的LSTM模型

LSTM神经网络解决了RNN梯度消失、对前层网络参数无法学习等问题，从而改进RNN，提高预测精度。LSTM是采取增加门控系统来解决RNN存在的问题[10]，故LSTM存在三个门：Input Gate、Output Gate、Forget Gate，单元结构图如图1。

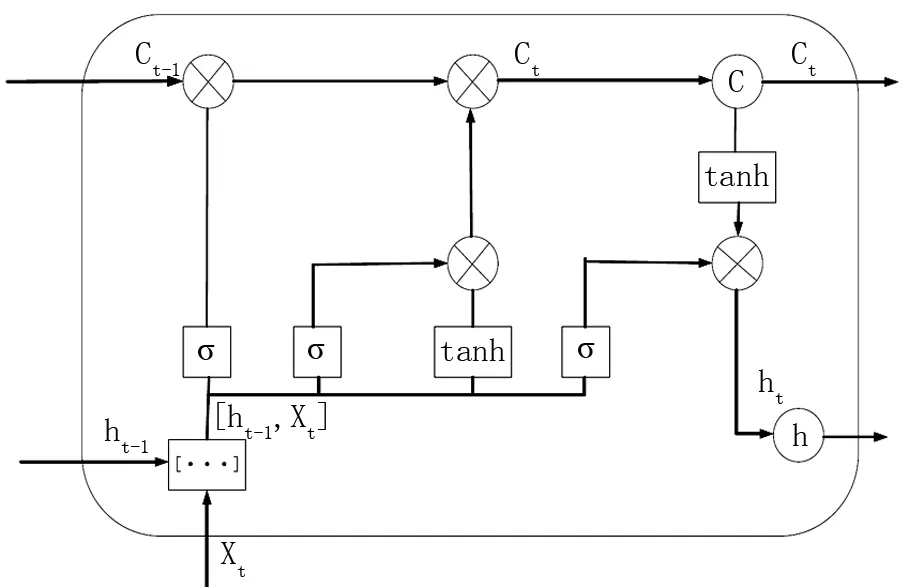
图1 LSTM单元结构图

Input Gate计算公式

it=σ(Wi·[ht-1,xt]+bi)

(1)

(2)

(3)

Output Gate计算公式

ot=σ(W0·[ht-1,xt]+b0)

(4)

ht=0t·tanh(ct)

(5)

Forget Gate计算公式

f(t)=σ(Wf·[ht-1,xt]+bf)

(6)

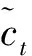
1.2 算法改进和参数优化

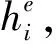
(7)

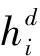
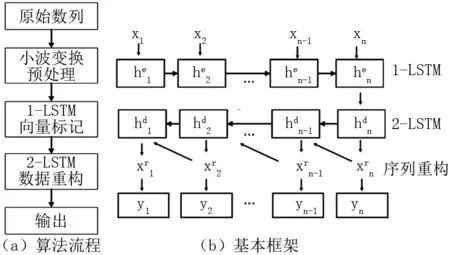
图2 改进LSTM算法

同时利用高斯过程作为先验函数，采用Expected-improvement(EI)作为采集函数，对1-LSTM和2-LSTM进行超参数优化。

2 LSTM-Prophet模型

2.1 Prophet算法

Prophet算法是Facebook发布的一个开源库，它是一个可分解的模型，即趋势、季节、节假日模型，它可以用非复杂且直观的参数对时间序列进行较高精度预测。但与其他较为经典的时间序列预测模型不同的地方在于，Prophet模型会先对序列采取周期性的分解，然后再预测。这样的预测方式，会突出数据中的节日效应和变化趋势，尤其当存在数据缺失、趋势突变和异常值的等问题的情况下，其鲁棒性效果优异。

Prophet把时间当做回归元，通过尝试拟合线性和非线性的时间函数项，通过采取与Holt-Winters指数平滑的类似办法，将考虑额外干扰因子季节因素进行建模[12]。整个过程可以分为四个部分：Modeling、forecast Evaluation、Surface Problems以及Visually Inspect Forecasts。

Prophet模型是自加性模型的一种，可以通过对趋势项建模、周期项建模和节假日项建模，从而分解时间序列，最终形成模型，故可表示为[13]

y(t)=g(t)+s(t)+h(t)+εt

(8)

其中：g(t)为趋势项，用于拟合序列中的非周期变化，包括分段线性增长，逻辑增长等。通常，Prophet采用线性模型进行预测。在对核心项趋势项进行建模时，当预测值是增长的情况时，也不是无限制性增长，将会存在一个可无限接近到达的最大极限值，此时该值这被称做承载容量(carrying capacity)，预测值在接近该值时将趋于饱和。

h(t)为节假日项，用于存在无规律性的节假日所带来的影响。法定节假日、重大事件或者突发事件会对序列产生很大的影响，数据波动会比较剧烈，而各较为稳定的节假日带来的波动在Prophet模型中是可以预测的。将各节假日设为一个模拟变量Di，共有L个虚拟变量，并且假设该模拟变量对客运量造成的影响为Ki，那么联立二者可得如下矩阵，从而将模型中纳入影响因子，达到提高模型预测精度的目标

Z(t)=[1(t∈D1),…1(t∈DL)]

(9)

h(t)=Z(t)K

(10)

s(t)用于周期变化，可称为周期项，该项较常使用傅里叶技术，表达式如下

(11)

式中:P是周期；an,bn是被估参数；t是时间；n是使用周期数的一半，N是使用周期的个数。Prophet模型在大多数情况下都是用来拟合连续时间段的时间序列，例如对年的周期性，P的值取365.25，N值取10，对周的周期性，P的值取7，N值取3。

εt用于反应未在模型中体现的异常变动，即误差项。

2.2 LSTM-Prophet算法模型

Prophet是单特征模型，其输入变量是仅输入两列，分别是设日期“ds”，数值输入“y”。有因为存在承载容量，故Prophet模型将有三种预测值。预测值设置为：预测值yhat，预测下界yhat_lower与预测上界yhat_upper。

在构建LSTM-Prophet算法模型时，首先根据优化后的LSTM模型，进行预测分析，再将预测结果作为输入进行Prophet算法预测，最后可得最终预测数值。

3 铁路月度客流量分析与预测

本文采用2005年1月～2018年12月的铁路月度客运量数据作为数据样本进行拟合建模分析，本文数据来源于国家统计局。通过LSTM-Prophet模型对2019年1～12月的月度数据进行预测，并对比分析该模型与传统灰色模型GM(1，1)，季节差分移动自回归模型(SARIMA)，LSTM神经网络的优劣，从而比较分析LSTM-Prophet模型。

3.1 改进的LSTM模型

采用PyTorch深度神经网络框架搭建本模型，实验在Intel(R)Xeon(R)CPU E5-2660 v2处理器和NVIDIA GeForce GTX Titan X显卡上进行。在对数据集做10 000次训练后，得到如图3的拟合情况，由图可知，拟合情况没有非常理想，预测精度不够高。

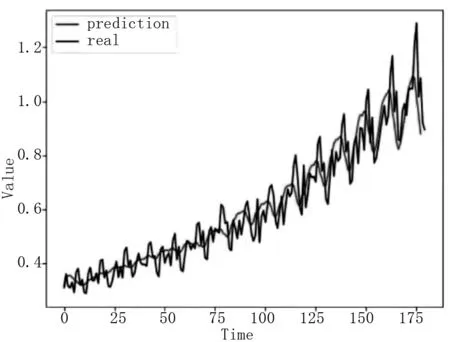
图3 LSTM预测拟合图

2019年各月度数据具体如表1，由表1可知，精度的波动略大，最高达15.25%，最低为0.01%。

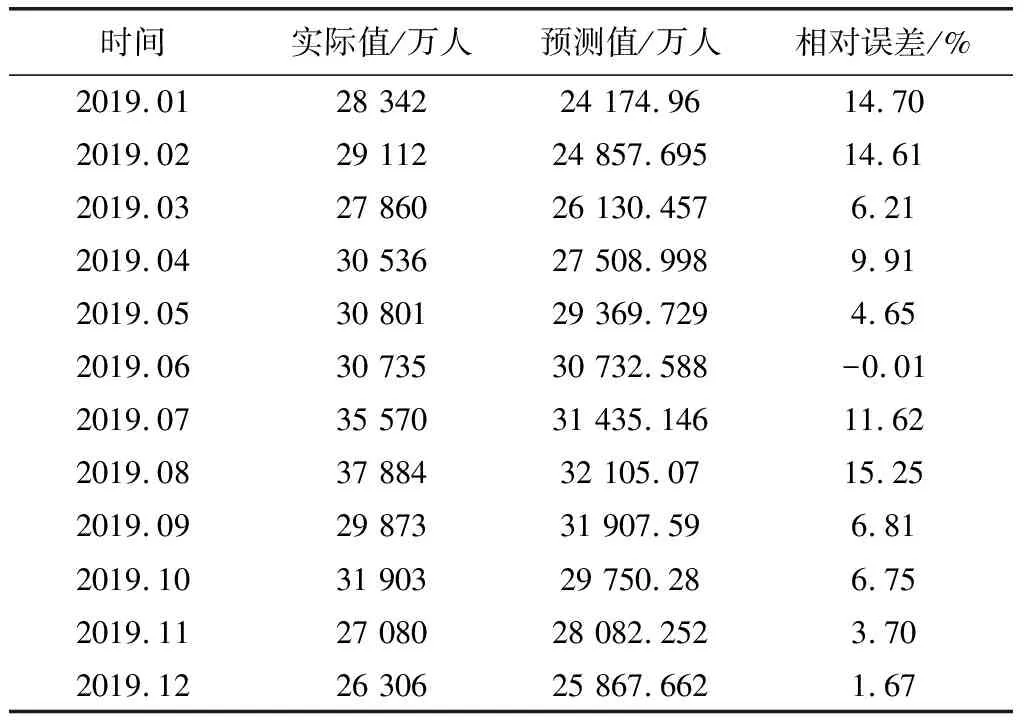
表1 LSTM预测值

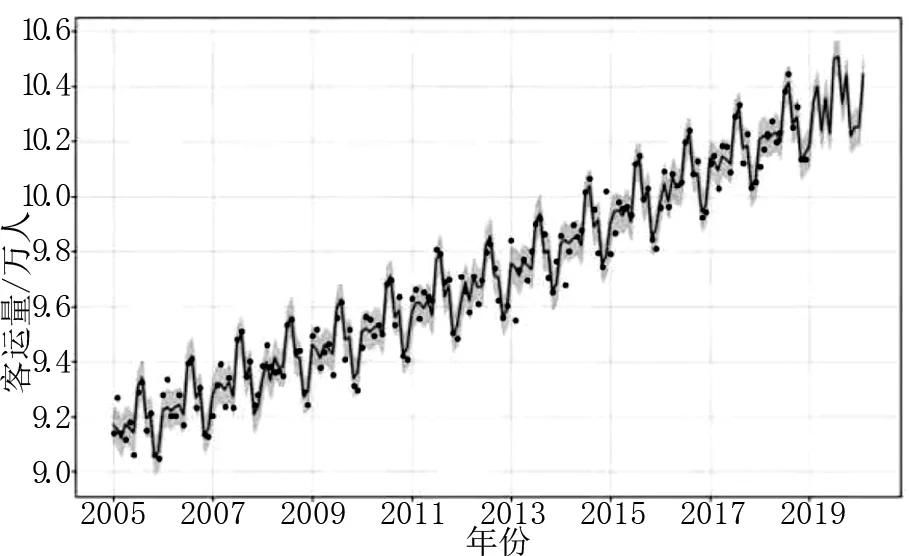
图4 LSTM-Prophet预测拟合结果

3.2 LSTM-Prophet模型

为建模的准确性与减小数据的振动幅度，故先将月度数据进行数据预处理，即将数据做log处理取其对数。又由于Prophet基本模型可知，Prophet模型是对天等连续时间的处理，所以如果直接用铁路客运量的月度数据进行拟合，那么结果将会误差很大，预测精度将会较低。为了解决这一问题，故将通过make_future_dataframe中传入频率参数的方式，让模型只做月度预测，从而达到预测要求。将改进后的LSTM模型预测值作为输入，得到拟合曲线如图4，结果如表2。

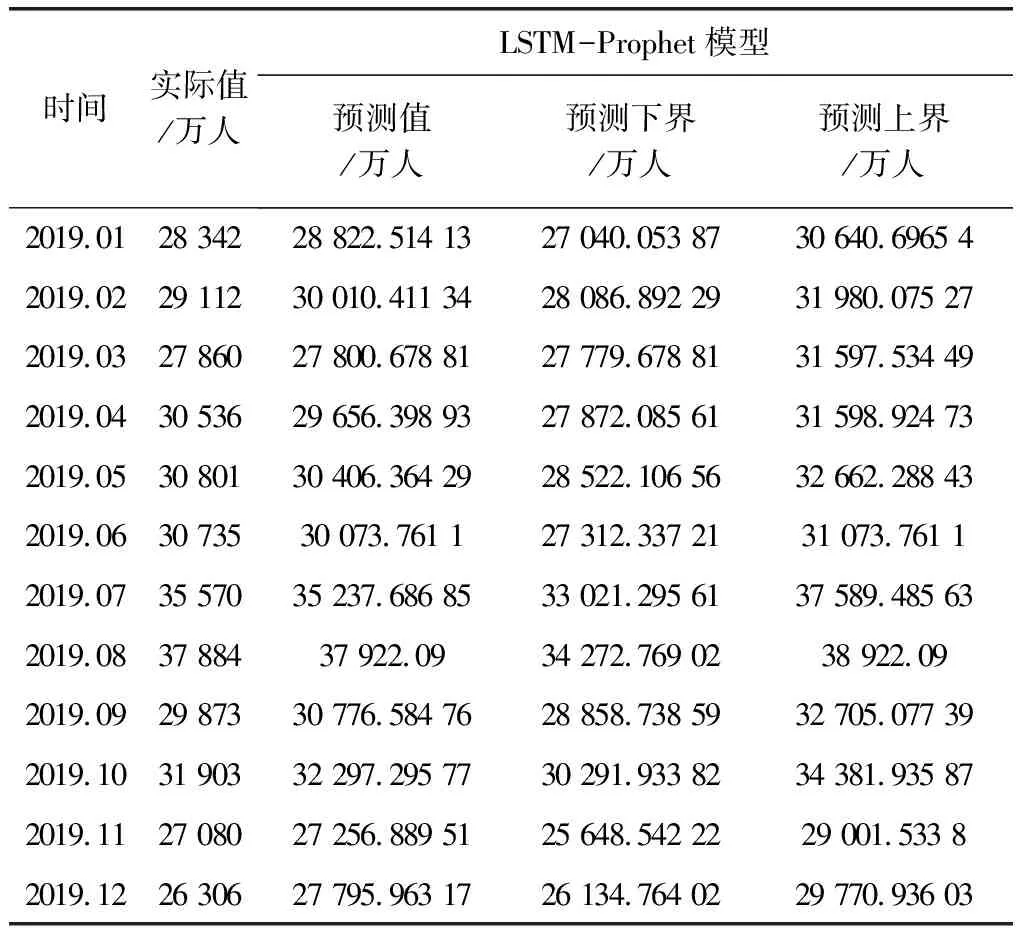
表2 LSTM-Prophet预测结果

3.3 模型对比

本文采用平均绝对百分比误差MAPE、平均绝对误差MAE与均方根误差RMSE为评价指标，指标计算公式如下

(12)

(13)

(14)

式中：Yt为预测值，yt为实际值，n为预测次数。

对比分析各模型的预测结果，用四种模型进行预测，比较四种模型的MAPE值、MAE值与RMSE值，其中LSTM-Prophet的MAPE值、MAE值和RMSE值均为最低值，分别为1.91%，559.07和691.82，全面优于GM(1，1)模型的8.75%，2 892.73和4 036.76、LSTM神经网络的7.99%，2 512.77和3 029.43与SARIMA(3，1，1)(1，1，1)12的2.76%，816.66和957.19。故得出GM(1，1)模型的预测精度是四种模型中最低的，其次为LSTM神经网络，再次为SARIMA(3，1，1)(1，1，1)12模型，Prophet模型精度为最高。所以LSTM-Prophet模型更适合用于预测铁路月度客运量，为规划提供参考，结果如表3。

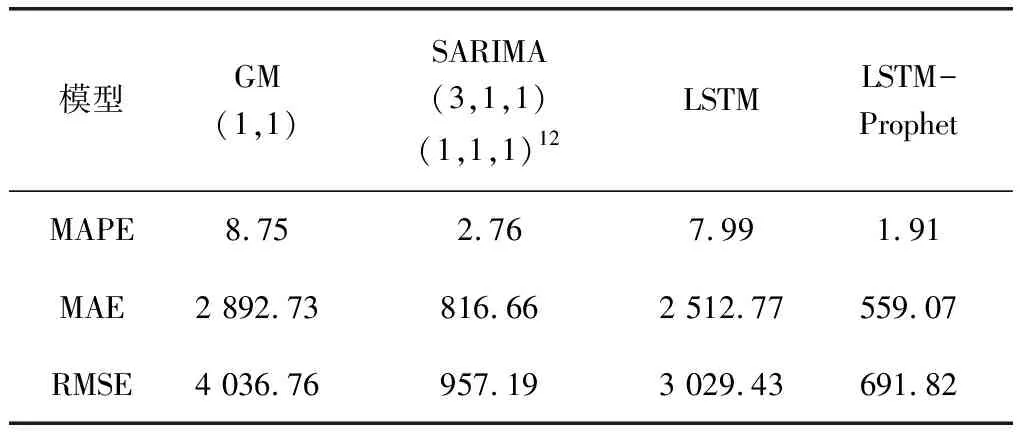
表3 四种模型对比表

4 结 论

LSTM-Prophet模型对于历史数据中包含的节假日效应有很强的敏感性，使其预测结果更加接近于预测值，从而提高预测精度。本文通过提取2005年1月～2019年12月的月度的季节性规律，改进优化了LSTM模型，并建立了LSTM-Prophet模型，且对2019年1～2月的客运量拟合预测，并与传统的GM(1，1)模型、SARIMA(3，1，3)(1，1，1)12模型和LSTM神经网络的预测结果对比分析，得出LSTM-Prophet模型更能准确预测铁路月度客运数据，对于研究铁路客运数据预测有一定参考意义，可对铁路部门开展工作提供参考价值。但该模型虽在遇到不可抗力因素时依旧无法及时准确做出调整，但可以根据预测数据了解因素对客运量的影响。