基于降维观测器与多胞体方法的执行器故障检测

朱芳来，李铭伟

（同济大学 电子与信息工程学院，上海 201804）

故障检测与隔离可用来检测系统中故障的发生并发出警示信号。实际系统往往由于组件失灵或运行条件的改变，系统的状态或性能发生意想不到的变化，这种现象可以归为系统发生了故障。故障检测与隔离（fault detection and isolation，FDI）的目的是当系统存在故障时产生警报信号（FD），并找出故障发生的位置（FI），以便后续采取相应的措施削弱或消除故障的负面影响。FDI方法可以分为基于模型的方法和基于数据的方法两大类别。在基于模型的故障检测方法中，基于观测器的FDI是最为有效的方法之一，该类方法目前已经取得了很多突出的研究成果［1-4］。例如，文献［1］针对离散广义系统，提出了一种基于H−/L∞观测器及多胞体残差构造的故障检测和隔离方法，该方法由于考虑了H−性能指标，相比传统的基于多胞7 讨论了互联系统的故障估计和调节问题。

近期一种特别的观测器——区间观测器，越来越受到学者们的关注。区间观测器不同于需要对系统状态进行渐近收敛估计或邻域稳定估计的Luenberger 观测器，它只需提供系统状态的一个稳定的上下界估计。与传统的Luenberger型观测器相比，区间观测器能更加便利地处理未知输入（外部扰动、执行器故障和模型不确定性）和非线性项。这是由于未知输入和非线性项的很大一部分信息，例如观测器匹配条件和Lipschitz条件等可以在区间观测器的设计中被忽略。由于这样的特点，区间观测器的研究得到了学者们的极大关注，并产生了众多的研究成果［5-11］。最近，多胞体理论被应用于离散时间系统，通过迭代计算得到包围系统状态的最小多胞体，以此得到系统状态的区间估计［12-14］。实际上，将多胞体理论应用于离散时间系统这一方法构成了一种特别类型的区间观测器。基于多胞体理论的FDI 方法近几年得到了极大的关注，并且有众多优秀的研究成果［15-16］。

基于观测器的FD 方法，通常要求所设计的观测器针对干扰鲁棒而对故障敏感，这样的观测器可以作为故障检测器。其主要技术手段之一就是构造合理的残差，通过残差来标志故障是否发生。如果采用基于Luenberger 类观测器的FD 方法，通常采用测量输出向量及其估计值的偏差构造残差。区间观测器作为一种未知输入观测器的特殊类型，其产生的残差区间估计实际上是残差天然的阈值。因而，基于区间观测器的FD 方法成为了基于模型FDI 方法的主要方法之一［17-21］。例如，文献［17］重点比较了基于集论未知输入观测器的方法和基于区间观测器方法的故障检测鲁棒性。文献［18］研究了具有有界扰动的离散线性变参数系统的故障检测问题。

针对执行器故障和扰动同时直接影响状态方程和输出方程的系统，本文基于Luenberger 型观测器和多胞体方法的结合研究执行器故障检测的问题。设计降维观测器并分析观测器误差动态系统的稳定性，使用多胞体方法提出状态的区间估计方法，并给出新的残差构造方法，实现执行器故障的检测。

1 离散系统的问题描述

在给出问题描述之前，先给出一些符号说明。

假设A=[aij]∈Rn×m和B=[bij]∈Rn×m，则A≤B⇔aij≤bij(i=1，…，n；j=1，…，m)。设A=[aij]∈Rn×m，max(0，A)=[αij]∈Rn×m，而αij=max(0，aij)。∀x∈Rn，diag(x)表示以向量x为对角元的n×n阶对角方阵。设M为对称方阵，M≺0表示M为负定矩阵。

考虑一类受到未知输入和执行器故障影响的离散时间线性系统

式中：x(k)∈Rn，u(k)∈Rm，y(k)∈Rp和η(k)∈Rq分别为系统状态，已知控制输入，可测量输出和未知输入。A∈ Rn×n，B∈ Rn×m，C∈ Rp×n和D∈ Rn×q为已知的常数矩阵。矩阵B和D为列满秩，而C为行满秩，并 有n≥p≥q。不 失 一 般 性，假 设C=[Ip O]。

假设1秩条件对所有满足|s|≥1的复数s成立。

对系统（1）中的干扰变量及其系数矩阵D做假设，如假设2。

假设2针对干扰η(k)，几乎所有的l≥q成立，有

且对其系数矩阵D，满足

引理1［22］假设1 和假设2 成立的充分必要条件为：对于任意正定对称矩阵Q∈ Rn×n，有如式（2）的Lyapunov矩阵代数方程组：

关于矩阵L∈ Rn×p和G∈ Rq×p以及正定对称矩阵P∈ Rn×n有解。

假设3对初始状态x(0)，存在2 个已知向量。对于未知输入η(k)，存在2个已知向量。

定义1n维s阶的多胞体Z是单位超立方体Bs=[−1，+1]s（s≥n）的仿射变换：Z=p⊕HBs={p+Hz，z∈Bs}，其中向量p∈Rn是多胞体Z的中心，而H∈Rn×s是多胞体Z的生成矩阵。这里符号⊕代表闵可夫斯基和。

性质1［13］

式中：p，p1，p2∈Rn，H∈Rn×s，H1∈Rn×s1H2∈Rn×s2和L∈Rl×n是具有相应维数的矩阵，符号⊙代表线性映射。

性质2［13］对n维s阶多胞体Z=p⊕HBs={p+Hz，z∈Bs} ∈Rn按照欧几里得范数降序排列矩阵H的各列得到矩阵。那么有d≤s），其中ℜd(H)=[Ha Hb]∈ Rn×d，Ha∈ Rn×(d−n)是由的 前d−n列构成，而Hb∈ Rn×n是对角矩阵，以1，...n) 作为其对角线元素。其中，代表矩阵的第i行第j列的元素。

性质3［13］对n维s阶的多胞体Z=p⊕HBs，∀x=[x1…xn]T∈Z，有

2 降维未知输入观测器设计

首先基于一个等价变换将原系统分解成2个子系统，其中一个子系统对干扰解耦。然后针对干扰解耦的子系统设计降维观测器，在无执行器故障发生的前提下，给出系统状态的估计。

对状态向量x，矩阵A、B、D、L和式（2）中的P写成分块形式

式 中 ：x1∈Rp，x2∈R(n−p)，A11∈Rp×p，A12∈Rp×(n−p)，A21∈R(n−p)×p，A22∈R(n−p)×(n−p)，B1∈Rp×m，B2∈R(n−p)×m，D1∈Rp×q，D2∈R(n−p)×q，L1∈Rp×p，L2∈R(n−p)×p，P11∈Rp×p，和P22∈R(n−p)×(n−p)。

对系统（1）作等价状态变换

其中K∈R(n−p)×p为之后需要确定的参数矩阵。在该等价变换下，有

由式（2）的第2 式并注意到C的特别形式可以得到[P12TP22]D=0，这意味着如果选取K=P22−1P12T，就有 [K In-p]D=0。于是得到

定理1在执行器无故障发生的情况下（fa(k)≡0），如果取，则

证明首先，注意到y(k)=z1(k)，然后式（3）的第2式减去式（4）的第1式得到降维观测器误差动态方程为

其中W=PL。进行矩阵分块展开，有

再经同等的初等行和列变换得到

再由Schur 补引理，知式（6）和式（7）分别等价于

其中，M=A11+L1+P11−1P12(A21+L2)。即在假设1和假设2下，式（8）与式（9）成立。而式（8）意味着式（5）是渐近收敛稳定的系统，于是有，证毕。

3 区间观测器设计与故障检测

针对式（3）的第1式所决定的关于z1(k)的动态系统，结合Luenberger型观测器和多胞体理论，提出一种能估计y(k)=z1(k)之上下界的区间观测器，以此提出一种执行器故障检测方法。

首先，对于式（3）的第1 式，考虑如式（10）的Luneberger型观测器：

证明事实上，当fa(k)=0 且η(k)=0 时，误差方程（11）变为

注意到y(k)=z1(k)，因 而。但由于干扰η(k)事实上的存在（即事实上η(k)≠0），因而观测器式（10）无法直接用于执行器故障检测器，因为观测器式（10）对干扰η(k)不具有鲁棒性。基于式（12）多胞体理论的结合提出一种对残差ey(k)的区间估计方法，且该区间估计在区间估计意义下是对干扰鲁棒的，以此提出一种执行器故障检测方法。

首先，由等价状态变换知z1(0)=Γx(0)，其中Γ=[Ip 0p×(n−p)]T，于是其中(0)是观测器式（10）设定的初值。再根据引理2知道

证明该引理的结论可以由多胞体性质4直接得到。

定理2在假设1、假设2、假设3 和fa(k)≡0 的前提下，基于动态系统（13），有

其中pk=Mpk−1+Dpη，Hk=[MHk−1DHη]。这里定义ℜd(H0)=H0，ℜd(Hk)(k≥1)的定义类似于性质2中ℜd(H)的定义。

其中pk=Mpk−1+Dpη，Hk=[MHk−1DHη]，根据数学归纳法，证毕。

推论1在假设1、假设2、假设3 和fa(k)≡0 的前提下，基于动态系统（11），则存在正整数N0>0，使得

其中pk=Mpk−1+Dpη，Hk=[MHk−1DHη]。这里定义ℜd(H0)=H0，ℜd(Hk) (k≥1)的定义，类似于性质2中ℜd(H)的定义。

其中Hε=εIn−p。基于式（11），知当k≥N0时，有

根据性质2，记为将矩阵[HkεA12]∈Rp×(d+q+n−p)各列按欧几里得范数降序排列而得到。记

由于ε充分小，所以1，...n) 作为其对角线元素。其中，代表矩阵1就是Hk各列按欧几里得范数降序排列后取其前d+q列，记为1，...n) 作为其对角线元素。其中，代表矩阵1。而1，...n) 作为其对角线元素。其中，代表矩阵2为εA12的各列按欧几里得范数降序排列而得到。根据性质2，有ℜd([HkεA12])=[HaHb]，其中，Ha为1，...n) 作为其对角线元素。其中，代表矩阵的前d−p列，也就是1，...n) 作为其对角线元素。其中，代表矩阵1的前d−p列。Hb为对角矩阵，其对角元素满足

所以有

同时有pk+ℜd(k)u=pk+Hau1+Hcu2。可见多胞体Z1比多胞体Z2包含的范围更广。

证明根据定理2和性质3，不难得出结论。

由于y(t)=z1(t)，所以有

使得在fa(k)≡0的条件下，有(k)≤y(k)≤(k)。

一个执行器故障检测逻辑如式（17）：

基于多胞体方法进行故障检测的方案可由图1简要描述。

图1 基于多胞体方法的执行器故障检测方案Fig.1 Actuator fault detection scheme based on Zonotope method

4 仿真案例

对所提出的降维观测器设计方法和基于多胞体理论的执行器故障检测方法给出仿真分析。炉温采样控制系统、电枢控制的直流伺服电机系统等真实世界中的连续系统均可进行等价离散化，以方便数字控制系统的设计。例如，电枢控制的直流伺服电机系统可选取角位移、角速度和角加速度作为状态变量，以角位移和角速度为输出，构建状态方程。参考文献［22］，系统（1）对应的系统矩阵为通过构建线性矩阵不等式，可得到代数矩阵方程（2）的解如下：

将矩阵P和L分块得到

首先验证无执行器故障发现下的降维观测器状态估计效果。为此，假设控制输入为u(k)=5sin(2k)，未知输入η(k)=sin(50k)，而fa(k)≡0。在执行器无故障发生时，根据定理1，降维观测器式（4）能产生原系统状态x3的渐进估计，其估计效果由图2c给出。图2a 和2b展示了x1和x2的区间估计。

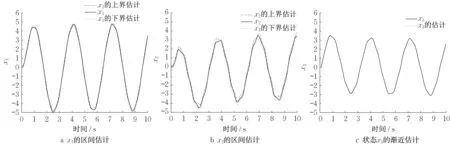
图2 状态的区间估计与渐近估计Fig.2 Interval estimation and asymptotic estimation of states

其次，为了体现基于多胞体的执行器故障检测效果，假设执行器故障信号为

基于式（18）的执行器故障检测方法的故障检测效果由图3给出。从图中可以看出5～15s时间段内执行器发生故障，此时残差信号给出了对应的示警。

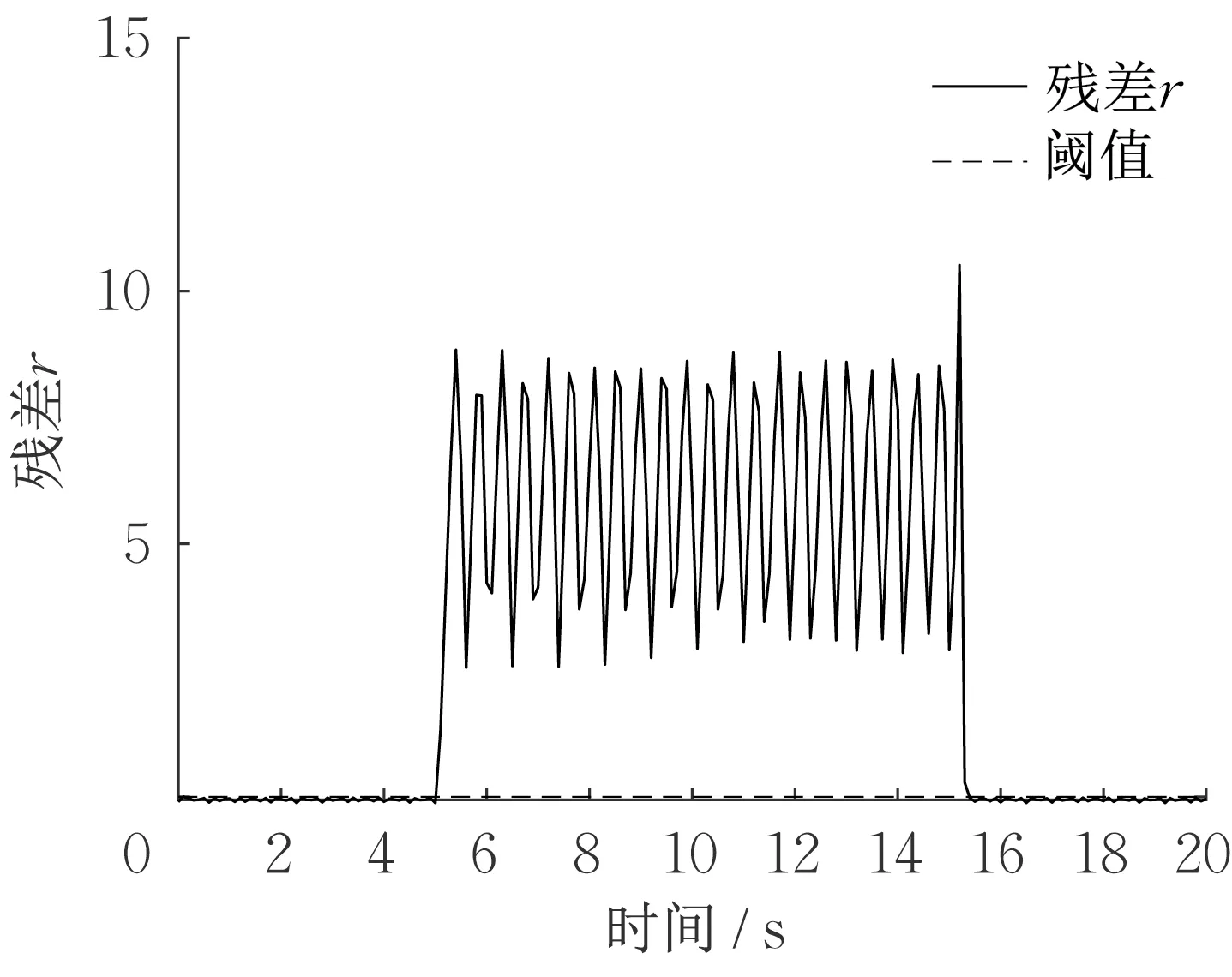
图3 存在执行器故障时的残差信号Fig.3 Residual signal in the presence of actuator fault

图4针对多胞体方法（zonotope method，ZM）和传统的区间观测器方法（traditional interval observer method，TIOM）的状态区间估计和故障检测效果两方面进行了比较。图4a展示了2种方法获取到的上界估计（upper boundary，UB）和下界估计（lower boundary，LB）。限于篇幅，仅呈现状态x1的区间估计。可以看到，由于估计偏差更小，采用ZM得到的区间估计优于TIOM。图4b展示了2种方法构建的残差。可见，由ZM法构建的残差对故障更敏感。

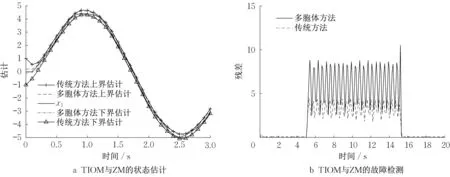
图4 传统方法与多胞体方法的对比Fig.4 Comparison of traditional method and Zonotope method

5 结论

针对离散系统研究了降维观测器设计方法及其Luenberger 型观测器和多胞体理论相结合的执行器故障检测方法。为了达到这样的目的，首先对原系统进行合理的状态等价变换，将原系统分解成2 个子系统。然后针对干扰解耦的子系统，提出了无执行器故障发生时的降维观测器设计方法。针对输出动态子系统，基于多胞体理论和Luenberger 型观测器的结合，提出了对输出误差的区间估计。基于输出误差的区间估计，构造残差实现了执行器故障检测的目的。如何将方法推广到连续系统将是下一步的研究议题。

作者贡献声明：

朱芳来：项目负责人，指导论文构思和论文修改。

李铭伟：论文构思和论文撰写。