一般灰数型面板数据关联分析模型及应用
吴鸿华, 刘思峰, 方志耕
(1. 南京航空航天大学经济与管理学院, 江苏 南京 211106; 2. 济南大学数学科学学院, 山东 济南 250022)
0 引 言
灰色关联分析是灰色系统理论的重要分支,用于根据各因素曲线几何特征来确定各因素间的相关程度[1]。在现实系统中,由于环境、认知等因素易造成收集的数据量小,具有“少数据,贫信息”的特征[2],因此,灰色关联分析模型已成功应用于经济管理[3]、医疗服务[4-6]、软件评估[7-9]、雷达分析[10]等多个实际领域,并取得了一系列成果。
自邓聚龙[11]提出邓氏关联分析模型以来,众多学者围绕灰色关联公理以及模型的构建进行了深入研究并取得了一些有价值的成果。研究的视角从点关联系数,到全局性或者整体性关联分析[2];从相似性视角,到接近性视角,再到综合性视角的关联分析模型[12]。近年来,研究的对象从一维序列拓展到面板数据。文献[13]基于二重积分和绝对关联分析模型首次构建了面板数据关联分析模型。文献[14]提出了三维关联分析模型,并将其应用于动态决策。文献[15]基于面板数据的时空特征构建了矩阵关联分析模型。文献[16]分别从时间维度和对象维度构建了灰色B型关联分析模型,并最终得到了三维灰色B型关联度公式。文献[17]考虑决策对象的截面信息和时间信息,定义了决策对象的发展状态矩阵和发展速度矩阵,并给出了各指标之间的距离,以此构建了灰色关联分析模型。文献[18]利用梯度描述面板数据的变化特征,提出了多元指标的灰色梯度关联分析模型。文献[19]将面板数据投射为空间网格, 构建了灰色相似性视角的关联分析模型。文献[20]描述了不同对象的时空特征,并构建了时空关联分析模型。文献[21]利用向量投影得到不同指标的关联系数,进而得到面板数据的灰色投影关联分析模型。文献[22]利用n维空间向量表述面板数据, 进而构建了相似性和接近性关联分析模型。
为了描述面板数据的空间特征,将其投射为空间曲线,文献[23]基于海塞矩阵及凹凸性构建了面板数据的凸关联分析模型。针对凹凸性描述空间曲线的不足,文献[24]利用有向曲率测度空间曲线的弯曲程度,并提出了灰色曲率关联分析模型。针对多指标多属性决策问题,文献[25]引入动态权函数,建立了面板数据的动态加权关联分析模型。进一步,文献[26]从时间维度建立了动态趋势关联分析模型。对于不同尺度的面板数据,文献[27]提出了不同尺度数据的多元灰色关联模型。
上述研究在一定程度上丰富了面板数据灰色关联分析理论,但仍存在以下不足:① 上述模型仅适用于实数型面板数据,对于一般灰数型面板数据无法进行分析。目前,由于一般灰数的运算有待进一步完善,利用一般灰数的运算或者距离测度进行相关性分析存在困难;② 现有的面板数据关联分析模型易受指标排列顺序的影响[16],即改变指标的排列顺序后,关联度的结果往往会随之改变。
为此,本文给出了一般灰数型面板数据的空间投射方法,并给出了重心三角曲面关联分析模型。首先,将样本矩阵分解为行为子矩阵;其次,给出行为子矩阵元素的核及上下界,并给出了由行为子矩阵元素相邻四点的上下界所确定的几何体的重心,得到由核及重心确定的三角曲面;然后,基于以三角曲面为曲顶的柱体体积构建了一般灰数型面板数据的关联分析模型;最后,通过实例分析验证了所提模型的合理性和有效性。
1 一般灰数型面板数据重心三角曲面的构建
为了更加准确地表征信息的不确定性,文献[28]给出了一般灰数的概念。
定义 1[28](一般灰数)设
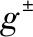
面板数据是将“截面数据”和“时间序列数据”综合起来的一种数据类型。当元素为一般灰数时,称为一般灰数型面板数据。
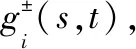
(1)

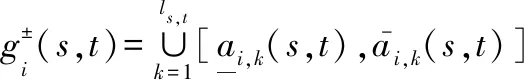
(2)
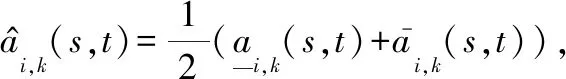
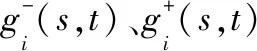
核作为灰数的代表,在灰数转化为实数运算的过程中具有不可替代的作用[1]。一般灰数的上下界表征了其边界信息。因此,一般灰数的核及上下界能够反映一般灰数的信息。
为解决样本指标排列顺序对关联分析模型结果的影响,下面给出样本矩阵分解为二元指标行为子矩阵的方法。
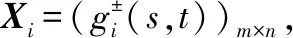
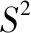
由指标sj1及sj2的数据构成的2×n矩阵记为
Xi(sj1,sj2)=
(3)
则称Xi(sj1,sj2)为Xi的二元指标sj1及sj2的行为子矩阵。
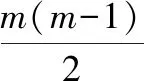
则称Xi(sj1,sj2,t)为Xi关于指标sj1及sj2在时刻t的行为子矩阵。
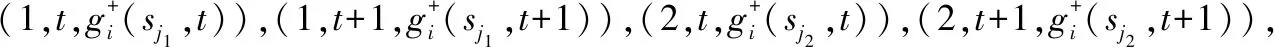
由空间几何学知识可得,上述几何体的重心为
(4)
其中,
将Xi(sj1,sj2,t)元素的核及重心对应空间中的点相连,并将同指标维度和同时间维度的核所对应的点相连,得到空间三角曲面,具体描述如下。
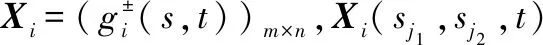
Xi(sj1,sj2,t)=
{Πk:Akx+Bky+Ckz+Dk=0,k=1,2,3,4}
Π1:A1=a-c,B1=a+c-2e,C1=1,D1=c-2a-t(a+c-2e),y-t+1≤x≤t-y+2,t≤y≤t+0.5;
Π2:A2=2e-a-b,B2=b-a,C2=-1,D2=(2+t)a+(1-t)b-2e,x+t-1≤y≤t-x+2,1≤x≤1.5;
Π3:A3=d-b,B3=b+d-2e,C3=-1,D3=(1-t)b-(2+t)d+(2+2t)e,t-y+2≤x≤y-t+1,t+0.5≤y≤t+1;
产业集群是区域产业发展的重要组织形式,既是拉动区域经济增长的发动机,又是促进区域创新的助推剂,也是提升区域竞争力的主流模式。位于山西省东南部的长治市。近年来,充分发挥资源优势、产业优势、技术优势,实施重点区域培育发展战略,通过集约化、规模化、园区化发展,着力培育壮大核心竞争力强、产业层级高、产业链条完整、特色优势突出的光伏产业聚集区。在打造山西重要的增长极、如期实现脱贫攻坚和全面建成小康社会“两个目标”的征程中不断取得新进展,开创新局面。数据显示,2017年,长治全市实现生产总值1477.5亿元,国内生产总值总量位列山西第二。
Π4:A4=2e-d-c,B4=c-d,C4=1,D4=(1-t)c+(2+t)d-4e,t-x+2≤y≤x+t-1,1.5≤x≤2。
上述定义说明,Xi(sj1,sj2,t)所对应的空间重心三角曲面由4个三角平面构成。
2 一般灰数型面板数据关联分析模型及性质
对于一般灰数型面板数据,由空间重心三角曲面作为曲顶的柱体体积可用于描述面板数据间的差异性。也就是说,曲顶柱体的体积值越接近,相关性程度越大,反之越小。
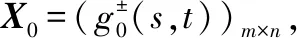
(5)
式中:V0(sj1,sj2)、Vi(sj1,sj2)分别表示由X0(sj1,sj2)、Xi(sj1,sj2)作为曲顶的曲顶柱体体积,称ε0i(sj1,sj2)为X0与Xi关于指标sj1及sj2的灰色重心三角曲面关联系数,记
(6)
则称ε0i为X0与Xi的灰色重心三角曲面关联度。
命题 1设系统的特征行为矩阵为X0,系统相关因素行为矩阵为Xi,关于指标sj1及sj2的行为子矩阵分别为X0(sj1,sj2)和Xi(sj1,sj2),则
(7)
(8)
证明以V0(sj1,sj2)为例证明,
V0(sj1,sj2)=
又由定义5可得
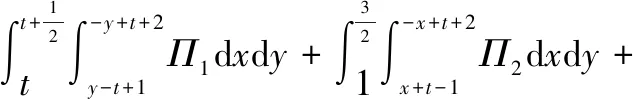
则
所以,
V0(sj1,sj2)=
证毕
命题1给出了一般灰数型面板数据行为子矩阵的重心三角曲面,并以此作为曲顶柱体的体积公式。当一般灰数退化为实数、区间灰数、三参数区间灰数时,得到以下推论。
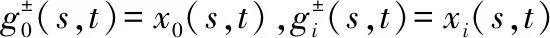
V0(sj1,sj2)=
(9)
Vi(sj1,sj2)=
(10)
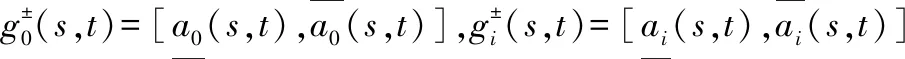
(11)
(12)
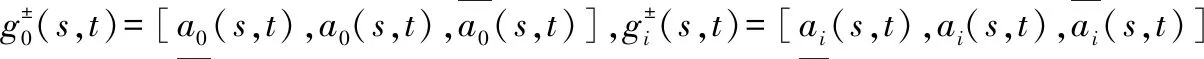
(13)
(14)
推论1~推论3表明,本文所提出模型同样适用于实数型面板数据、区间灰数型面板数据以及三参数区间灰数型面板数据。
定理 1一般灰数重心三角曲面关联度ε0i满足如下性质:
(1) 规范性:0<ε0i≤1;
(2) 接近性:V0(sj1,sj2)与Vi(sj1,sj2)越接近,ε0i越大;
(3) 自反性:ε00=εii=1;
(4) 对称性:ε0i=εi0;
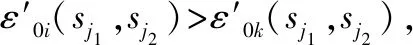
(7) 关联度ε0i不受指标排列顺序的影响。
证明(1) 由于
|V0(sj1,sj2)-Vi(sj1,sj2)|≥0
则0<ε0i(sj1,sj2)≤1,所以0<ε0i≤1。
(2) 当V0(sj1,sj2)与Vi(sj1,sj2)越接近,|V0(sj1,sj2)-Vi(sj1,sj2)|的值越小,则ε0i(sj1,sj2)越大,即ε0i越大。
(3) 当X0=Xi时,显然V0(sj1,sj2)=Vi(sj1,sj2), 则
|V0(sj1,sj2)-Vi(sj1,sj2)|=0
则ε0i(sj1,sj2)=1,所以ε00=εii=1。
(4) 对于任意两指标sj1,sj2,显然有
|V0(sj1,sj2)-Vi(sj1,sj2)|=|Vi(sj1,sj2)-V0(sj1,sj2)|
则ε0i(sj1,sj2)=εi0(sj1,sj2),所以ε0i=εi0。
又
则
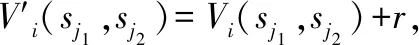
(V0(sj1,sj2)+r)|=|Vi(sj1,sj2)-V0(sj1,sj2)|
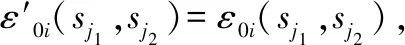
同理可得
又由于
ε0i(sj1,sj2)>ε0k(sj1,sj2)
则
|V0(sj1,sj2)-Vi(sj1,sj2)|<|V0(sj1,sj2)-Vk(sj1,sj2)|
由于u≠0,则
|u‖V0(sj1,sj2)-Vi(sj1,sj2)|< |u‖V0(sj1,sj2)-Vk(sj1,sj2)|
即
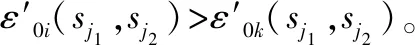
(7) 由于S2包括指标集所有可能的二元组合,而Xi(sj1,sj2)所对应的曲顶柱体的体积与指标sj1及sj2的顺序无关,即Vi(sj1,sj2)=Vi(sj2,sj1),所以ε0i与样本矩阵的指标排列顺序无关,不受指标排序的影响。
证毕
定理1中的性质(1)和性质(2)说明ε0i满足灰色关联度公理,即满足规范性和接近性公理。
3 实例分析
国内复杂装备研发项目大多采用“主制造商-供应商”的管理模式,大量关键组件需要国际、国内供应商的协作与配合。因此,确定供应商方法的科学性将会影响项目的成败。作为复杂装备的关键组件决策问题,供应商通过“招投标”方式完成。一般由主制造商提出具体要求,各家供应商根据要求制定投标方案。由于是复杂装备,主制造商需要引入第三方对供应商进行评估。主制造商结合供应商提交的方案以及第三方的评估,选择最优方案。由于方案的提交信息以及第三方评估视角的不同,最终得到的信息或是实数,或是区间灰数,或是上述的组合等,可用一般灰数来描述。
在某关键器件供应商选择决策中,首轮有三家供应商(U1,U2,U3)入围。决策指标包括产品状态(s1)、供货能力(s2)、服务能力(s3)。主制作商委托第三方对这三家供应商进行评估,结合供应商提供的信息,得到三家供应商2017~2020年的相关数据,决策矩阵如下:
X1、X2、X3由一般灰数构成,下面利用所提出的关联分析模型选择最佳供应商。
由于三个决策指标均为效益型指标,选用
进行规范化处理。
inf(X3)。
核矩阵分别为
上界矩阵分别为
下界矩阵分别为
基于灰数相对核排序准则[29],选择三家供应商的各指标、各时间点的最大值作为理想点X0,其中核矩阵、下界矩阵、上界矩阵分别为
根据灰色重心三角曲面关联系数式(5),得到决策指标二元组合的关联系数,如表1所示。
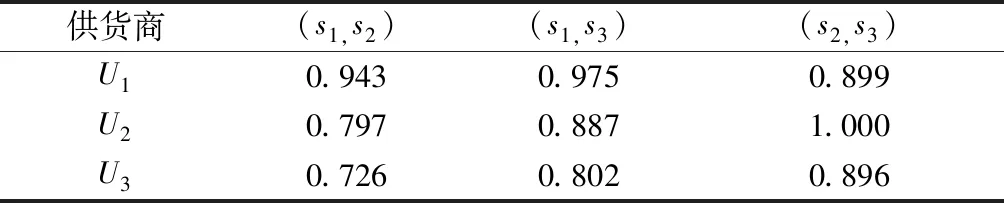
表1 三家供应商的关联系数
利用关联度式(6),得到三家供应商与理想点的关联度:ε01=0.939,ε02=0.895,ε03=0.808。关联序为ε01≻ε02≻ε03,具体排序为:供应商U1,供应商U2,供应商U3。供应商与理想点的关联度越大,供应商的方案越优,因此选择U1作为该关键组件的供应商。
从具体数据来看,X1的数值整体较大,数据从2017~2020年逐渐变大,可见选择供应商U1符合实际情况。X2数据的变化也有逐渐变大的趋势,但数值较X1整体更小。X3与X1、X2相比,数值波动较大,特别是产品状态指标。可见,本文的结果能够反映数据的相关程度。
根据文献[30]的关联分析模型,计算得到σ01=0.744,σ02=0.559,σ03=0.624。关联序为σ01≻σ03≻σ02,结果也是选择U1作为该关键组件的供应商,但供应商U3排在供应商U2的前面。事实上,无论从整体数值还是数据的变化趋势来看,X2应该优于X3。可见,文献[30]尽管能够选择出供应商,但未能对该三家供应商进行有效的排序。
4 结 论
本文针对一般灰数型面板数据构建了重心三角曲面关联分析模型。与以往的关联分析模型相比,一方面,所提出的模型基于面板数据的几何特征,不受一般灰数运算规则的影响;另一方面,基于数列的排列组合原理,解决了指标排列顺序对关联度影响的问题。所提出的模型满足规范性、对称性、数乘变换关联序不变性等性质。通过实例分析了模型的有效性和合理性,结果表明所提模型能够表征一般灰数型面板数据的相关程度。

