基于多时段变参数SEIQR模型的流感病毒传播研究

何洋文，周大勇，方 铭，马永峰

(大连交通大学 a.土木工程学院；b.理学院；c.机械工程学院，辽宁 大连 116028)

公共卫生事业是公共事业的重要组成部分，与人们的健康、学习、工作及生活有着密切的关系[1]。流感是一种由流感病毒引起的呼吸道传染病，传染性强，传播面广，极易在青少年和老年人等免疫力低的人群中传播，特别是在学校这种相对密集和封闭的环境中，传染病的高发期极易导致病毒的大范围传播[2]，因此对于传染病的研究尤为重要。

利用信息技术对传染病进行预防和预测是公共卫生事业非常重要的部分，可通过建立多时段变参数微分方程模型来研究突发流感的演化规律。

1 模型建立与求解分析

1.1 模型假设

对病毒传播过程中的部分因素进行假设(包括人数变化和采取的措施等)，以达到简化模型的效果，为模拟疫情传播提供基础条件。

假设在疫情传播阶段，学校学生总人数不变，分为易感者、潜伏者、感染者、康复者、隔离者。假设：传播过程中每个学生被感染后的发病时间相同。在校外不发生传播、不存在超级传播者、每个学生自愈能力相同。

表1 符号说明Tab.1 Symbol description

1.2 多时段变参数SEIQR模型

1.2.1 建立多时段变参数SEIQR模型

采用传染病动力学模型，结合疫情传播情况，甲型H1N1流感病毒在传播初期一般不易被察觉，此时的传播特征符合传统SEIR模型的传播特点[3]，但是传统的SEIR模型建立在外力无干预的情形下不能处理采取一定防控措施带来的变化[4]。但疫情发展到一定阶段时，人们会采取防控措施，并会时刻根据疫情的发展不断调整防控措施。针对疫情传播特点，建立多时段变参数的SEIQR传染病模型，根据各时期的传播特点改变相关参数，以获得更加真实合理的模拟效果，得出更加准确的结果。关于SEIQR模型分析如下：根据流感病毒的流行病学特征，将人群分为S、E、I、Q、R，建立(S-E-I-Q-R，SEIQR)模型[3]。具体传播流程如图1、图2所示。

其中，β为传染率，即易感者被感染为潜伏者的概率。

图1 流感病毒传播初期的SEIQR模型流程图Fig.1 Flow chart of the SEIQR model of early transmission of influenza virus

图2 流感病毒传播后期的SEIQR模型流程图Fig.2 Flow chart of the SEIQR model of late transmission of influenza virus

不同概率计算过程如下：β：与病毒传播性质、传播时间有关。β1和β2参考具体实例。a：假设平均潜伏期为A，a=1/A。隔离率t：假设感染者平均隔离时间为B，g=1/B。康复率p：假设平均发病时间为C，p=1/C。

SEIQR模型动态全过程分析如下[4]：已知总N=S+E+I+Q+R人群保持不变。某一时刻t，根据不同人群发生变化建立模型：

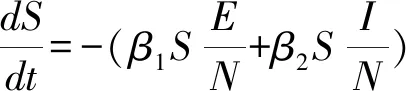
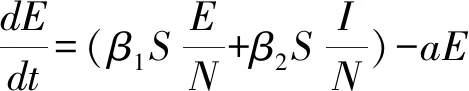
已知SEIQR模型。根据t时刻各类人群人数，可预测(t+1)时刻各类人群人数：

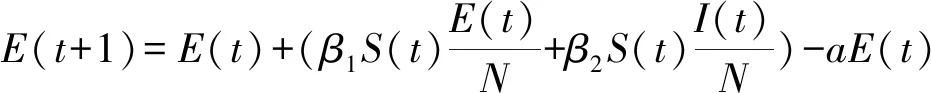
感染人群：I(t+1)=aE(t)-gI(t)

隔离人群：Q(t+1)=gI(t)-pQ(t)

康复人群：R(t+1)=pQ(t)

1.2.2 采取隔离措施的SEIQR模型

甲型H1N1流感病毒有潜伏期短和传染性强的特点，主要发生于儿童、老人等抵抗力弱的群体[7]。在疫情发展的中后期，通常会采取一定的隔离防控措施，阻断病毒传播。由于E在疫情中难以被发现，所以隔离措施只针对I。模拟疫情不同时期采取的隔离措施，分析疫情变化情况。隔离期间，假设病例病情发展过程与未隔离者相同，康复率仍为p，则t时刻，从Q中康复人数为pQ，假设康复者永久免疫[8]。

1.2.3 采取隔离+疫苗接种的SEIQR模型

冬春季节是流感的高发季节，尤其需要注意儿童的防护。其中接种疫苗是预防病毒感染的关键，虽然疫苗不能100%预防，但不接种疫苗被感染的概率则是0或100%[9]。通过模拟在采取一定隔离措施的情况下，接种疫苗对疫情防控的作用和在不同接种率下疫苗对疫情的有效控制程度，以反映疫苗在疫情防控中的重要性和必要性。

1.2.4 甲型H1N1流感病毒模型参数估计

通过查阅文献资料，根据模拟事件的数据可知，甲型H1N1流感病毒的平均潜伏期为2 d，病程为3～5 d[10]，结合事件数据，综合选择潜伏期为2 d，病程为4 d，β2=0.125，取其潜伏期的传染率为感染期的86%，即a=0.5、p=0.25、k=0.86、β1=0.108。

2 模型的评估与讨论

2.1 甲型H1N1流感病毒传播事件模拟

此次模拟的为某省较偏远地区小学的一起流感病毒感染事件[10]，主要传播途径为人际传播，通过分析每日新增感染者人数(如表2所示)，可将流行曲线分为3个阶段。第1阶段为6月13—26日，为病毒传播初期，26日开始调查采样，之前未采取任何防护措施；第2阶段为6月27—28日，此时实验室确定病毒为甲型H1N1，并落实控制措施；第3阶段为6月28日—7月10日，此时控制措施生效，新增感染者逐日下降。

表2 学校每日新增数据Tab.2 New data added daily in school

基于SEIQR算法，运用MATLAB软件进行拟合优度计算，拟合效果如图3所示。计算得曲线拟合结果R2=0.863，P=0.000，证明此次拟合曲线与实际情况拟合效果较好。

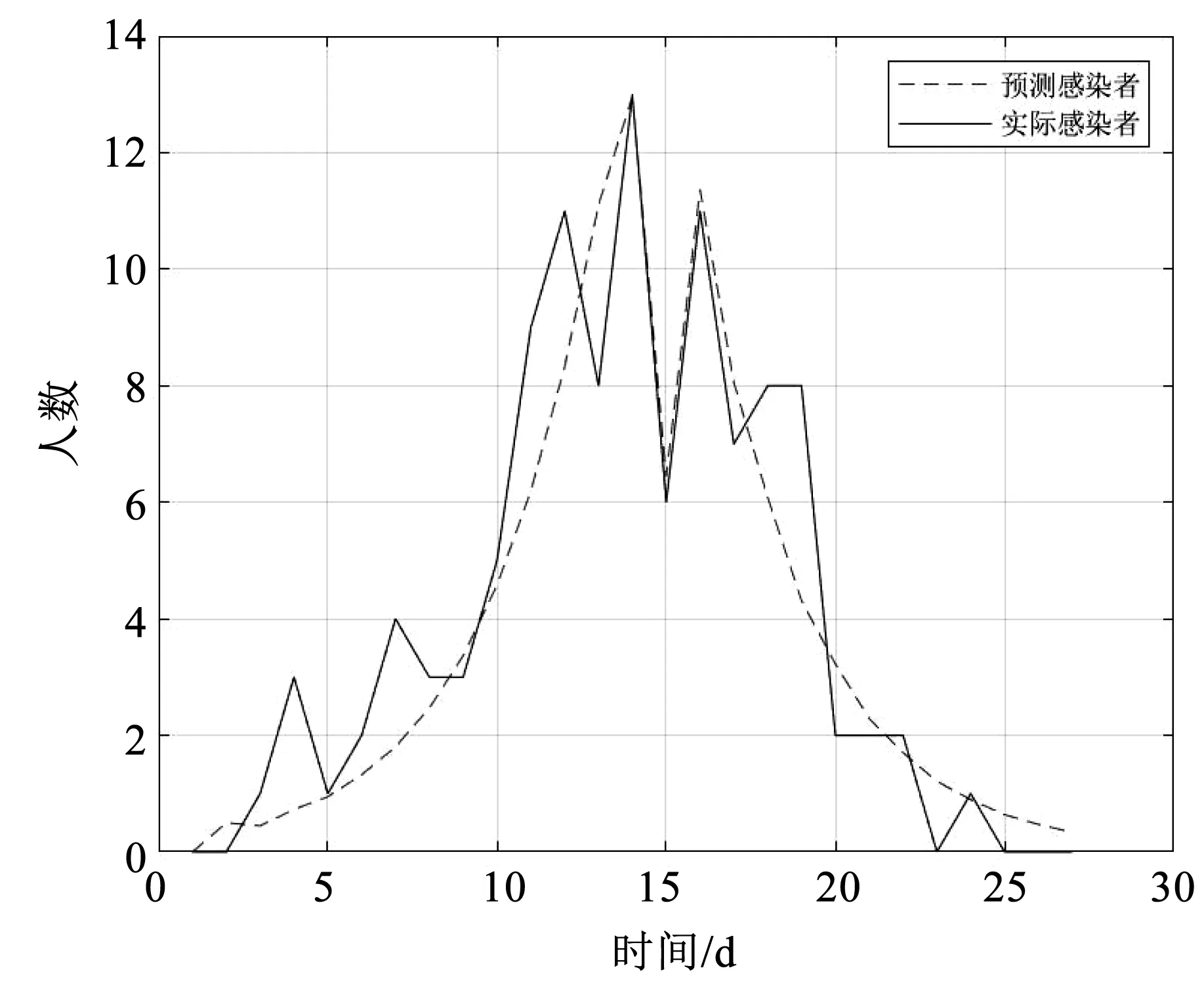
图3 甲型H1N1流感爆发疫情与模拟拟合结果Fig.3 Influenza A (H1N1) outbreak and simulation results

2.2 采取不同防护措施下的模型分析

2.2.1 无任何防护措施下的疫情分析

在没有任何防护措施的情况下，疫情的传播模型为SEIR模型。分析模拟结果可知，若此次疫情未采取任何防护措施，则共有565人感染流感病毒，患病率为63.13%，疫情持续40 d，在疫情发生的第21 d，新增病例数最多为47例，如图4所示。实际该校累计报告病例110例，患病率为12.29%。对比可知，在无防护措施的情况下，患病率要增加50%以上，疫情多持续13 d左右。

图4 无防护措施下甲型H1N1流感疫情模拟Fig.4 Simulation of influenza A (H1N1) epidemic without protection

2.2.2 采取及时隔离措施的疫情分析

分析图5模拟结果可知，如果CDC在调查取样当天仅实施隔离，疫情的峰值和感染人数都会比实际要高；如果CDC在疫情传播第10 d采取隔离措施，则疫情的峰值会更早到来且处于一个较低的状态。越早实施隔离措施，疫情持续的时间和峰值到来的时间越短，对于疫情的控制也愈有利。

图5 隔离措施下甲型H1N1流感疫情模拟Fig.5 Simulation of A (H1N1) influenza epidemic under quarantine measures

2.2.3 采取隔离+接种疫苗的疫情分析

模拟在第14 d采取隔离措施，分析学生的疫苗接种率分别为10%、30%和50%时的疫情传播情况。分析图6的模拟结果可知，疫苗接种率为30%时，疫情就基本被控制住，且随着疫苗接种率的提高，疫情的发展得到了明显抑制。由于模拟未考虑疫苗的防护效果不是100%，所以实际情况会比模拟结果略高，但是趋势是一致的。研究表明，疫苗的保护率为45.15%～100%，免疫成功率达到80%以上[11]，且当疫苗接种率达到70%时，甲型H1N1流感的发病率不足30%[12]，所以随着疫苗接种率的增加，疫苗保护率的影响越低。

图6 隔离+接种疫苗措施下甲型H1N1流感疫情模拟Fig.6 Simulation of influenza A (H1N1) epidemic under quarantine + vaccination measures

2.3 传染病模型灵敏度分析

2.3.1 灵敏度相关参数分析

由于本次模型使用的参数a、p、k是通过查阅文献资料和疫情数据综合确定的，所以参数存在一定的不确定性。为了评估参数不确定性下输入变量对模型失效概率的影响[13]，需对这些参数进行灵敏度分析。结合文献资料，参数的取值区间分别为a=0.3～1(潜伏期为1～3d)，p=0.2～0.3(病程为3～5d)，k=0.8～0.9，根据不同区间，在区间内分别取a1=0.4、a2=0.6、a3=0.7；p1=0.2、p2=0.3；k1=0.8、k2=0.9，对数值进行SEIQR模型的灵敏度分析。

2.3.2 灵敏度分析

运用MATLAB软件得出各个参数结果，通过分析结果可知，模型对参数a、p、k具有一定的敏感性，但模型的变化率均在合理范围内，模拟的曲线间的变化情况如图7、8、9所示。

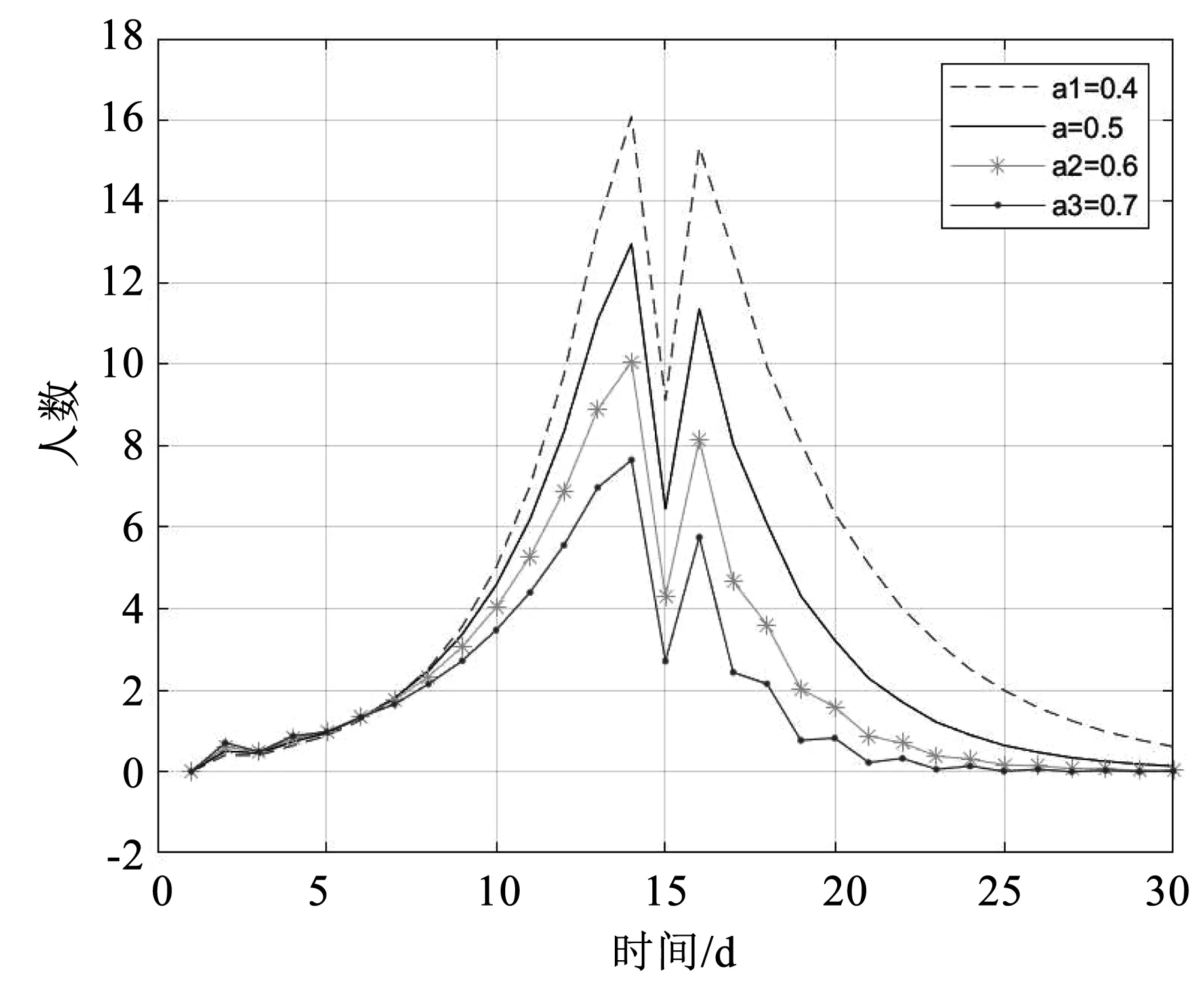
图7 模型对参数a的灵敏度Fig.7 Sensitivity of the model to parameter a

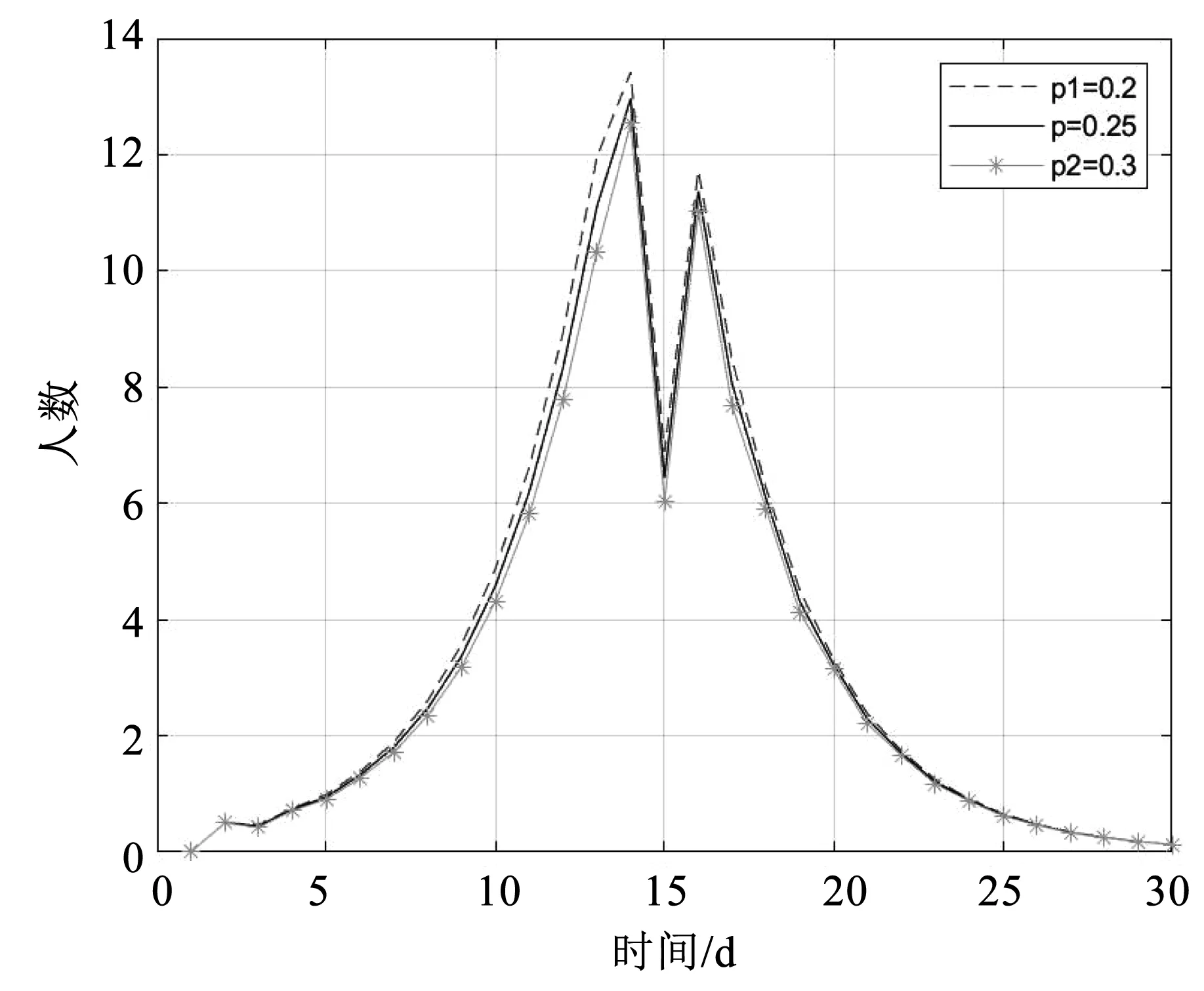
图8 模型对参数p的灵敏度Fig.8 Sensitivity of the model to parameter p

图9 模型对参数k的灵敏度Fig.9 Sensitivity of the model to parameter k

3 结束语

综合考虑在疫情实际传播中可能遇到的情况建立多时段变参数的SEIQR模型，针对疫情传播过程中采取的措施，将疫情传播分为数个时段，根据每个时段内的防控措施优化模型参数，模拟疫情传播中的变化情况，分析得出在接种疫苗的基础上，即使没有及时采取隔离防控措施，依然可以及时有效地控制住疫情发展，此研究结果对其他传染病的模拟与预防具有一定的参考价值。由于模型参数的不确定性，运用灵敏度分析方法，对不确定的参数进行可靠性灵敏度分析，通过分析最后的模型图像，评估输入参数对模型的影响均在合理范围内。