考虑配网电压支撑整体最优的SVG配置方法
内蒙古电力(集团)有限责任公司巴彦淖尔供电分公司 姚志东 刘易 国网浙江台州市黄岩区供电公司 董继
1 引言
SVG配置的现有研究聚焦于减少网损、降低投资费用等。李国成等[1]研究以线损和投资费用最小为目标的最优配置问题,无功设备的最优配置点由灵敏度分析得到。胡晓阳等[2]引入无功补偿分布因子,以确定无功设备的候选位置和容量。上述方法并未分析SVG 对配网电压的整体提升效果。于晓军等[3]将最优配置与可靠性评估结合,得出无功补偿装置的最优配置方式。余健明等[4]从最大节约网损的角度出发,结合配电网络自身的特点确定无功装置补偿点的位置。这些方法主要从降低费用角度考虑整个配电网无功装置的配置。现本文提出一种SVG接入后对配电网电压整体提升效果最优的配置点确定方法。
2 SVG接入对配电网电压的影响
SVG接入的配网示意图如图1所示。
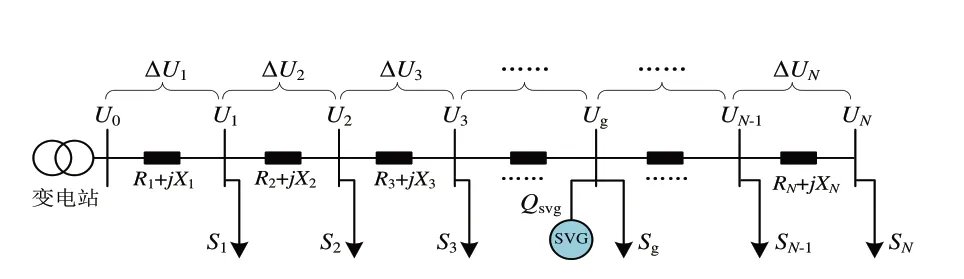
图1 SVG接入的配电网示意图
设馈线上共N个用户,第n个用户视在功率为Sn=Pn+jQn;线路始端为节点0,与配电网变电站二次侧相连接;线路上第n户所在位置电压为Un;第n-1 个用户和第n个用户之间线路阻抗为Rn+jXn;SVG注入线路的无功功率为Qsvg。
2.1 SVG未接入配网时
假设配电网均为辐射型馈线,忽略馈线中的功率损耗,且定义线路中有功功率和无功功率向负载方向流动为正方向,反之为负方向。
SVG 接入前,第m与m-1 个用户之间压降为式(1):
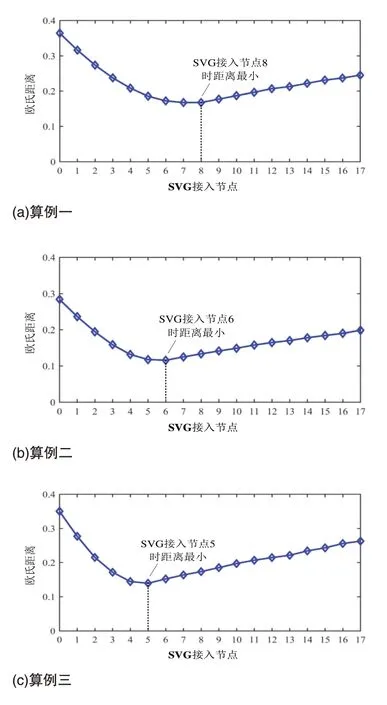
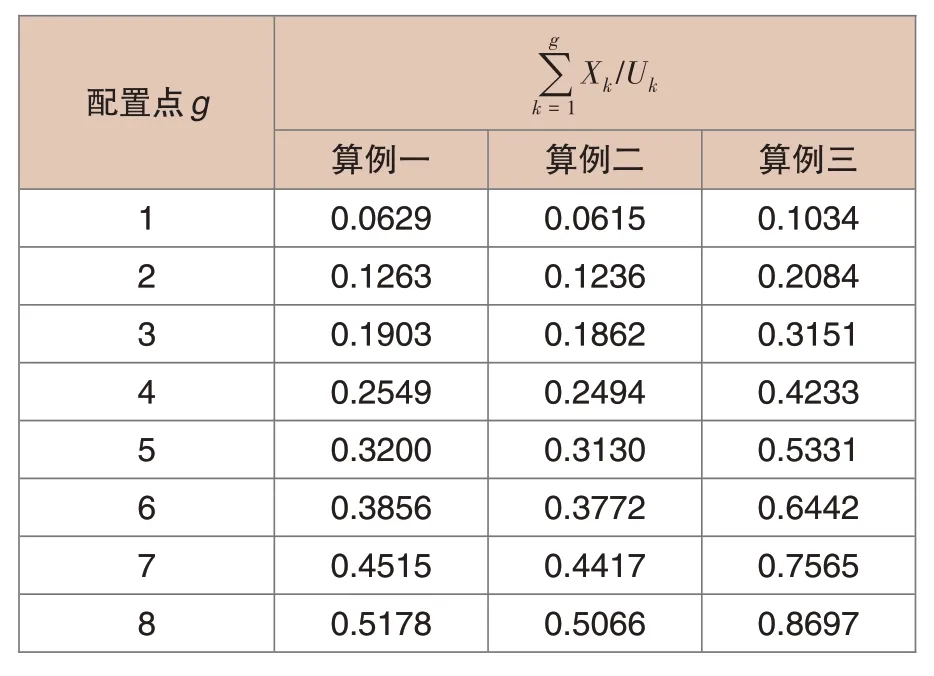
用户消耗的有功功率Pn和无功功率Qn均大于0,故ΔUm>0,Um 式(2)中:U0为线路初始端电压。 2.2.1 用户位于SVG配置点上游 SVG接入后,用户位于SVG配置点之前或与其同配置点时(即0 图2 用户位于SVG配置点上游 用户位于SVG 配置点前节点的电压计算如式(3): 由上级电网故障等原因产生电压暂降时,线路各节点电压均会下降,此时SVG向电网注入无功功率以支撑电压,此时Qsvg>0,反之Qsvg<0。此时相邻节点的电压差为式(4): 2.2.2 用户位于SVG配置点下游 当用户位于SVG 配置点之后时,即g 图3 用户位于SVG配置点下游 用户位于SVG 配置点后节点的电压计算如式(5): 此时相邻节点的电压差为式(6): SVG配置点前后的节点电压如图4所示。 图4 SVG配置点前后的节点电压 本文以最小化电压暂降对线路各节点电压的影响作为目标。在最优配置点处电压水平将被抬升到暂降前水平。根据潮流分布,最优点之后各节点电压也将提升至暂降前水平。设图4所示g点为SVG最优配置点,则g点及其后各节点电压均应补偿至暂降前水平。设暂降幅值为ΔU,暂降后且未治理时的电压幅值为U′m,则有式(7): 式(7)中:Um,B在数值上与Um相同,U′m在计算方式上与Um相同。整理可得式(8): 式(8)中各变量均为有名值。将式(8)左侧定义为最优配置指数OAI,即得式(9): 最优配置指数OAI的大小决定式(8)右侧g的取值,也就决定了SVG的接入位置。 本文采用欧氏距离判定SVG接入不同节点后对电网电压的整体支撑效果,计算方法如式(10): 式(10)中:Ui和U′i分别为暂降前后各节点电压幅值。 参考图1,在Simulink 中搭建仿真模型。算例参数为馈线含18 个节点,各节点所接负荷参考IEEE33 算例的主馈线各节点的负荷参数。仿真时,SVG遍历接入不同节点。SVG可发出或吸收的最大无功功率为3.0MVar。 为验证本文所述SVG最优配置点确定方法,设定3 个不同的算例进行比较。各算例下的暂降幅值与线路阻抗如表1所示。 表1 各算例下的暂降幅值与线路阻抗 SVG依次遍历接入线路中各节点,仿真得到不同节点接入SVG后各节点与暂降前各节点电压之间的欧氏距离对比。不同算例的节点电压欧氏距离对比如图5所示。 图5 不同算例的节点电压欧氏距离对比 在不同算例中,均存在一节点接入SVG后使得对线路电压整体补偿效果最好。由图5(a)中可知,算例一中在节点8 接入SVG 时,各节点电压与暂降前电压的“距离最短”,即补偿效果最好。对比图5(b)、5(a)可知,暂降幅值减小,在节点6接入时首先达到补偿前水平,相对算例一的节点8,最优点向线路首端偏移;对比图5(c)、5(a)可知,线路参数增大,在节点5 接入时首先达到补偿前水平,相对于算例一的节点8,最优点向线路首端偏移。上述变化与由式(8)对应。 本节将对三种算例下最优配置点的选择进行理论验证,3种算例中且配置点g取值不同时,式(8)右侧取值如表2所示。 表2 式(8)右侧取值 对于算例一,OAI 值为0.4869,位于区间[0.4515,0.5178]中部,接入7 或8 节点的电压支撑效果相似,为使得最优点后节点电压恢复暂降前水平,工程上一般在节点补偿,可以规定这种情况下选取节点8 作为最优点;对于算例二、三,OAI值分别为0.3617 和0.4869,分别靠近[0.3130,0.3772]的右端点与[0.4233,0.5331]的右端点,这两种算例中分别选择节点6、5作为最优配置点时对线路电压整体支撑效果最优。仿真结果与式(8)所确定的最优配置点结果一致,验证方法的正确性。 对于辐射网,馈线中存在一个SVG 最优配置点:电压暂降时,该点接入SVG后能够有效地提高配网整体的电压水平。本文提出SVG接入辐射网的最优配置点确定方法,适用于存在大量敏感负荷的辐射型配网,能够充分利用无功补偿装置的无功容量,提高配电网的供电质量。2.2 SVG接入配网后
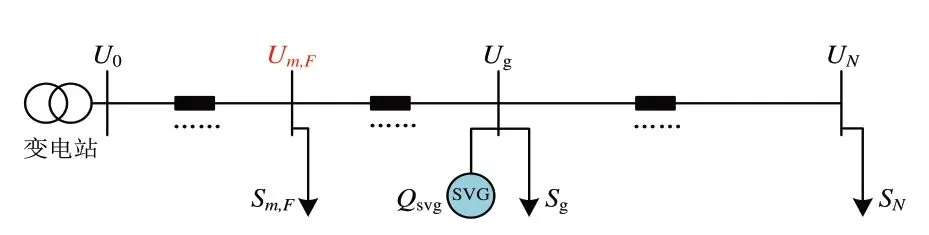
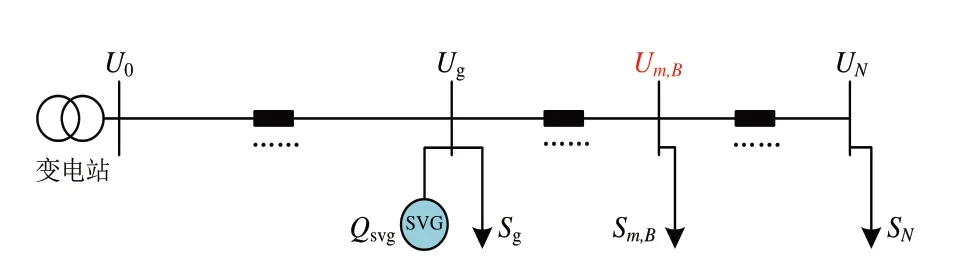
3 考虑电压支撑的SVG最优配置点
3.1 SVG最优配置指数
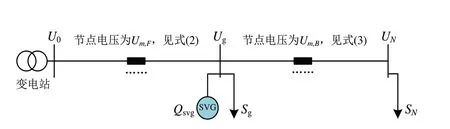
3.2 配置效果的判定
4 算例分析
4.1 算例简介
4.2 电压支撑效果分析
4.3 本文方法的验证
5 结语

