大剂量多孔无针注射器结构优化

刘国勇 ，李帆 ，李新月 ，陈雪波 ，朱冬梅

（1.北京科技大学 机械工程学院，北京 100083；2.东风本田汽车有限公司，湖北 武汉 430056）

目前，国内外普遍采用不锈钢制成的注射针对人体进行药液注射.针头的穿刺会引起剧烈的疼痛，且给药时针头侵入体内，容易传播病毒、细菌，传播烈性传染病，因此，对其消毒措施要求很高.此外，有针注射器多为一次性使用，后续的回收处理比较麻烦.所以无针注射方式越来越引起关注.

国外对无针注射的研究起步较早，早在1866年，法国科学家Béclard 首次提出了“无针注射”的概念.相较于传统有针注射，无针注射方式具有药效更好、疼痛感更轻等优点，所以无针注射方式逐渐成为药物注射、传染病防治的最佳选择［1-2］.Mohizin 等人分析了药液注射介质对微孔射流的渗透和分散影响机理，其研究表明：介质的黏弹性、介质间的界面类型和注射深度都影响了药液的注射过程［3］.Rane 等人通过数值模拟，得到了流体的流变和微孔几何形状对射流特性的影响，同时将研究扩展到非牛顿流体，认为其流变特性可通过Carreau 模型进行近似，还阐明了不同流变参数对射流特性的影响［4］.Na⁃kayama 等人通过CFD 模拟，分析了无针注射器的流场特性.通过移动边界方法模拟了药液在安瓿内部的流动过程，并使用LES/VOF 方法对流体的动力学过程进行了建模［5］.Williams 等人通过使用计算流体动力学方法和实验观察来研究微孔的几何形状、流体黏度和黏性热对射流过程的影响［6］.Schoubben 等人模拟计算了不同条件下的射流力、射流速度以及射流的持续时间，且将聚丙烯酰胺凝胶用于模拟皮肤软组织，研究了不同注射剂量随时间变化的射流过程［7］.Mohizin 及Rane 等人针对无针注射器的流场进行了研究，通过试验和仿真结合的方式，分析了药液黏度及驱动压力等参数对流场特性的影响［8-9］.Zeng 等人通过无针注射实验，定量分析了微孔直径及注射体积对药液分散过程的影响［10］.

反观国内研究现状，虽然我国在无针注射技术这一领域起步相对较晚，但近些年来关于无针注射的项目工作也在陆续地展开.其中：陈波等人基于FLUENT 软件对无针注射器的工作全过程进行了数值模拟，得到了驱动压强与出口射流速度间的变化规律及药液在皮肤内的扩散过程［11］.宋飞洋及陈添禹等人对无针注射进行了仿真建模及实验研究，得到了无针注射器的几何参数对射流特性、活塞杆受力等因素的影响［12-13］.

虽然关于无针注射方面的研究较多，但并没有解决其单次注射剂量小的问题，传统单孔注射器单次注射剂量仅0.3～0.5 mL［14］，这是限制无针注射推广的主要原因，同时对其注射机理尚未形成完整的理论体系.本文旨在提出一种大剂量的多孔无针注射结构，注射器的最大注射剂量可达5 mL，并对其结构进行优化，为大剂量无针注射的设计及使用提供参考.

1 模型建立

1.1 无针注射器二维模型的建立

大剂量多孔无针注射器的模型建立是基于陈雪波对单孔无针注射模型的研究［15］，其研究得出单孔采用收缩角为20°、长径比为1.4 的无针注射微孔取得较好的出口速度.本文以此为基础得到多孔无针注射器的结构，如图1所示.

图1 多孔无针注射器结构示意图Fig.1 Schematic diagram of the structure of multi-hole needlefree injector

微孔采用3孔结构，3孔分布如图2所示.为提高流量，需增大无针注射器安瓿的尺寸.方法有二，一是增加安瓿的直径，二是增大安瓿的长度.考虑注射时间和动能损失，选择增大安瓿的直径.单孔无针注射器的工作速度为150 m/s，通过仿真注射器的入口压力，使多微孔的针头的射流速度能达到150 m/s［16］.其中长径比为l/d，收缩角为α，微孔直径为d，总长度为L，收缩段长度为L2，分布圆直径d1采用德国市面上的一款无针注射器产品injex30 的参数，同时为增加单次的注射剂量，安瓿直径为 5 mm，该安瓿内部各个尺寸如表1所示.

表1 多孔无针注射器内部尺寸Tab.1 Internal dimensions of multi-hole needle-free injector

图2 3孔分布示意图Fig.2 Schematic diagram of distribution of 3 holes

建立无针注射器内部流场的三维模型如图3 所示，并对其进行网格划分，划分的网格如图4 所示，采用非结构化网格，收缩段及微孔处进行网格加密，并设置边界层.

图3 注射器模型Fig.3 Model of the injector

图4 注射器网格Fig.4 Grid of the injector

网格划分之后导入FLUENT.实际的无针注射过程中，射流流动是瞬态过程.为简化计算，可考虑某一时刻流动状态，选择基于压力-速度耦合的稳态求解器，采用VOF 多相流模型，湍流模型选用标准κ-ε两方程湍流模型，边界条件设置为：入口压力为 10 MPa、11 MPa、12 MPa、13 MPa、14 MPa、15 MPa，出口为压力出口（出口为大气），算法采用默认的SIMPLE 算法，采用入口初始化后进行迭代计算，迭代至残差曲线收敛.

1.2 网格无关性验证

数值模拟精度受网格的数量和质量及现有资源配置的影响，选择合适的网格数目计算具有重要意义.因此在数值计算之前，开展网格无关性检验.分别划分五种不同的网格方案，通过数值计算，以出口速度为参考，入口压力设为14 MPa，选取计算结果较为稳定的网格数.计算结果如表2 所示.在网格大于23 万时，出口速度仿真结果与最大网格数仿真结果偏差在0.1%以内，考虑计算准确性和计算机配置，选取方案3进行仿真.

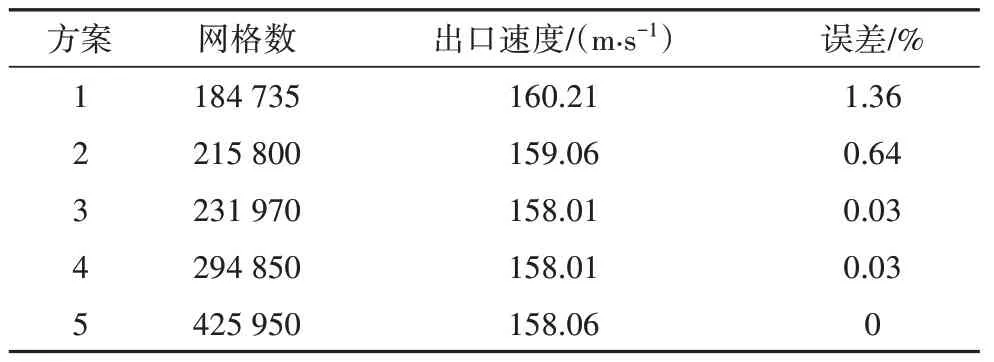
表2 三维模型网格无关性验证Tab.2 Grid independence validation of 3D model

2 内部流场数值模拟

分析不同入口压力（10 MPa、11 MPa、12 MPa、13 MPa、14 MPa、15 MPa）所对应的多孔内部流场.由图5 可以看出：药液在收缩段加速，在出口处速度达到最大值.

图5 入口压力为10 MPa下的速度云图Fig.5 Velocity contour at inlet pressure of 10 MPa

根据文献，出口速度超过150 m/s 时药液可穿透皮肤层，到达皮下组织，从皮肤溢出量大大减少［16］.无针注射器的压力为13 MPa 时，其平均速度达到了151.67 m/s，满足注射要求.为保证注射过程的有效性，将其入口压强定为不小于13 MPa，该高压有助于药液击穿皮肤，方便后续的低速药液进入皮肤.

图6 是不同入口压力下出口速度最大值和均值的曲线图.其速度均值是由出口处所有节点的速度经平均得到的.由图可知：出口速度随入口压力增大而增大，且最大速度和平均速度增长趋势基本一致.

图6 不同入口压力下的出口速度最大值和均值Fig.6 Maximum and mean values of outlet velocity at different inlet pressures

3 多孔无针注射器应力分析

3.1 流固耦合模型

流固耦合分析的目的是：在较高的入口压力下，观察安瓿的应力分布情况，通过调整安瓿的结构参数，降低内部的最大应力，使其在重复工作中保持较高的安全系数.利用ANSYS 上的Workbench 平台进行单向流固耦合.

安瓿的材料要求为密度小、无毒、溶水性低、耐腐蚀、无色透明、抗冲击性强、可加工性好，据此可以选择ABS树脂作为安瓿的材料.根据文献，测出的其应力应变曲线如图7 所示，其杨氏模量为2 ✕109GPa，在Workbench 的材料库添加该材料并编辑其物理属性［17］.

图7 ABS测试应力应变曲线Fig.7 Stress-strain curve of ABS test

对流体区域进行网格划分，并进行计算，待计算收敛后将流场计算的结果导入Static Structure 模块进行单向的耦合分析.边界条件设置：安瓿和收缩段固定连接，在安瓿侧面即抓握面施加固定约束，导入流场计算载荷进行计算.

3.2 结果分析

计算13 MPa、14 MPa、15 MPa 这些常用压强下的不同的安瓿直径对应的最大等效应力，其结果见表3.

表3 不同安瓿直径对应的最大等效应力 单位MPaTab.3 Maximum-equivalent stress of different ampoule di⁃ametersunit MPa

从表3 中可以看出，随着安瓿直径的增加，其最大等效应力减小；随着入口压力的增加，其最大等效应力增加.ABS 的屈服应力约为48.2 MPa，所以安瓿直径最小为6.5 mm.考虑材料ABS 树脂工作时受到冲击载荷，有较大的危险性，安全系数取3～5，则可算出当安全系数为5 时，入口压力为13 MPa、14 MPa、15 MPa 时对应的许用应力分别为7.7 MPa、8.28 MPa、8.88 MPa.计算符合该安全系数的最小安瓿直径，首先做出不同入口压力下最大等效应力变化曲线如 图8 所示，对图8 中的曲线进行6 次多项式拟合，拟合出的多项式分别为：

图8 最大等效应力随安瓿直径变化曲线Fig.8 Curves of maximum equivalent stress with ampoule diam⁃eter

根据拟合出的多项式，代入y得到许用应力值为7.7 MPa、8.28 MPa、8.88 MPa，求得对应入口压力13 MPa、14 MPa、15 MPa 下安瓿的最小直径x分别为11.2 mm、11.9 mm、12.2 mm.

4 无针注射器结构优化

通过对大剂量无针注射器的流场仿真和流固耦合分析，得到了入口压力对无针注射器出口速度的影响规律，以及对应的大剂量无针注射器的最小外径.下一步基于最小外径11.9 mm 和驱动压力14 MPa，设计正交试验，综合考察各项参数对大剂量无针注射器的影响程度，设计优化参数方案，进一步通过流固耦合分析校核设计结构强度是否满足要求.

4.1 正交实验设计

正交法是一种广泛使用的方法，采用正交试验法可以简单计算各因素对实验结果的影响，通过图表形式表现出来，再通过极差综合比较，最后确定优化参数.在工艺参数优化过程中收缩段的收缩角、长径比、分布圆直径、收缩段长度和微孔直径等设计变量的取值范围相当重要，关系参数优化过程的搜索效率.基于陈雪波的仿真结果得到收缩角、长径比的大致范围［15］，根据实际情况选择分布圆直径、收缩段长度和微孔直径.

1）收缩角α，根据陈雪波［15］的单孔仿真结果选取10°、15°、20°、25°四个值.

2）长径比l/d，根据陈雪波［15］的单孔仿真结果选取1、1.2、1.4、1.6四个值.

3）分布圆直径d1（mm），考虑药液喷射过程中较小的分布圆能使注射伤口相对聚集以及收缩段干涉问题，选取2、2.2、2.4、2.6四个值.

4）收缩段长度L2（mm），根据injex30产品的长度在3.5～4.5 mm，选取3.9、4.05、4.2、4.35四个值.

5）微孔直径d（mm），考虑较小的直径能更好地集中压力以达到更高速度，选取0.105、0.135、0.165、0.195四个值.

影响多孔无针注射器出口速度的主要因素为收缩角α、长径比l/d、分布圆直径d1、收缩段长度L2、微孔直径d，并假设各因素之间不存在交互作用，选取4个水平，得到表4.

表4 影响出口速度指标的因素与水平Tab.4 Factors and levels affecting outlet velocity index

根据因素及水平划分，采用五因素四水平的正交试验矩阵，采用正交表L16（45），考核指标为出口速度v，得到相应的正交表.

在表5 中考察五因素四水平对出口速度的影响，所有不同的试验条件共有45个.根据正交试验设计，安排16 组仿真试验，实验的目的是得到对出口速度影响最大的参数以及各个工艺参数对出口速度影响优先级，最后得出最佳参数组合.把各参数不同水平下实验结果均值的最大值和最小值之差称为极差，极差越大对结果影响越大，反之，影响越小.从表中可以明显看出各参数对指标（出口速度）的影响大小，即：

表5 L16（45）无针注射器参数正交试验直观分析表Tab.5 L16（45）data sheet of orthogonal test and results

通过极差分析可知：影响出口速度最主要的因素是收缩角和微孔直径.根据文献［18］，微孔直径在0.039～0.559 mm，出口速度在180 m/s附近时，注射深度比较理想.考虑出口速度过大对皮肤的切割范围会很大，患者的不适感会增加，所以最优方案选择A3B3C1D2E4，即选择20°收缩角、1.4的长径比、2 mm 的分布圆直径、4.05 mm 的收缩段长度和0.195 mm 的微孔直径.针对得到的方案，考虑较小的微孔直径在切割皮肤过程中对人体的损伤更小，故选择0.165 mm的微孔直径.

4.2 无针注射器最优参数应力分析

根据正交试验得到的最优参数方案，如表6 所示，建立大剂量无针注射器的实体模型，如图9所示.材料采用ABS 高强度树脂，在Workbench 平台材料库中添加材料并设置材料属性.对流体区域进行网格划分，并进行计算，待计算收敛后将流场计算的结果导入Static Structure 模块进行单向的耦合分析，求解得到无针注射器的总变形云图和等效应力云图分别如图10和图11所示.

图9 无针注射器实体模型Fig.9 Entity model of needle-free injector

表6 大剂量无针注射器优化参数表Tab.6 Optimal parameters of the large dose needle-free injector

从图10 和图11中可以看出，最大变形和最大应力都出现在收缩段的入口处，且安瓿基本没有任何变形和较大应力.无针注射器工作过程中，薄壁结构收缩段出口处流体有较大的压力和速度变化，会对收缩段产生很大的压力，导致在此处产生最大应力.ABS 的屈服应力为48.2 MPa［19］，无针注射器整体最大应力为46 MPa，基本满足ABS材料的要求，可以证明参数正交优化结果的合理性.

图10 无针注射器总变形云图Fig.10 Total deformation contour of needle-free injector

图11 无针注射器等效应力云图Fig.11 Equivalent stress contour of needle-free injector

5 优化方案验证

通过3D打印和激光打孔加工技术得到与表6优化结果尺寸参数一致的安瓿.通过高速相机和速度分析软件进行注射速度的采集及分析，同时通过动力学分析，来验证优化方案的可行性.

5.1 试验方案

试验方案如图12 所示，将高速相机采集到的图片序列导入速度分析软件MicroVec3，同时考虑到实际的无针注射中皮肤与微孔的间距通常为2 mm 左右，则采集与微孔间距为0 mm、2 mm、5 mm、10 mm、15 mm 的各个截面上若干点的速度，再取平均值即可近似得到该截面的速度.

图12 试验方案Fig.12 Test program

5.1.1 注射过程时间及速度的计算

注射过程的总时间，可以根据相机帧数及拍摄的有效图片的张数得到，即式（4）：

在MicroVec3 软件中，将已知的实际尺寸（此处选择安瓿的外径）作为参照尺寸，进而确定图像放大率（zoom rate），再通过高速相机的帧数得到跨帧时间（straddle time），速度放大率通过式（5）可获得：

通过监测同一点在一个跨帧时间内的移动距离，再通过式（6）即可得到整个注射过程各个点的速度值.

综上，即可得到不同采集截面的平均速度随注射时间的变化曲线，根据此曲线可得到整个注射过程的相关规律.

5.1.2 安瓿内部停滞压强的理论推导

5.1.2.1 药液喷射过程分析

图13 为无针注射器的简化模型，可以从动能守恒的角度建立微分方程.

图13 无针注射器简化模型Fig.13 Simplified model of needle-free injector

由于安瓿内部药液的速度远小于音速，可假设药液为不可压缩的无粘流体.令h=(L1-xp)，则安瓿内部药液的动能T可表示为：

式中：ρ为药液的密度；Ap为安瓿储药内腔的截面面积；L1为药液装载的长度；xp为活塞的位移.

由于药液从出口射出而造成的动能损失率可表示为：

式中：vout为出口速度；A0为安瓿出口截面面积.

由能量守恒可知，安瓿内部动能的变化率等于推杆对药液做功的功率减去药液从出口射出造成的动能损失率，即：

式中：P为安瓿内部的压强.

由流体的连续性方程可知：

将公式（10）代入公式（9）中，可得：

5.1.2.2 药液推杆的受力分析

图14 为药液推杆的受力示意图，根据牛顿第二定律可知：

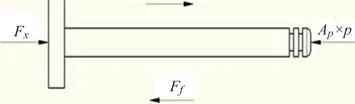
图14 药液推杆受力示意图Fig.14 Schematic of force for the rod

式中：Ap×p为药液停滞压强产生的阻力；mp为活塞杆的质量；k为弹簧的刚度系数；x0为弹簧的总压缩量.

忽略推杆与安瓿之间的摩擦，式（12）可进一步简化：

联立式（11）、式（13）即得完整的无针注射器的动力学方程：

5.2 试验设备

试验采用的无针注射装置如图15 所示，其主要由动力源（弹簧）、安全锁、连接件和安瓿组成.图16即为安瓿端部的微孔，其收缩角为20°，孔径为 0.165 mm.

图15 无针注射装置Fig.15 Device of needle-free injector

图16 安瓿上的微孔Fig.16 Micro holes of the ampoule

试验现场的高速相机的主要参数如下：相机型号为FASTCAM Nova S9，相机帧数为22 500.

5.3 试验结果分析

5.3.1 无针注射动力学方程结果分析

无针注射整个过程的动力学方程中所有已知的参数如表7所示.

表7 无针注射器动力方程参数表Tab.7 Dynamic function parameters of the needle-free injector

将以上的已知参数代入式（14），通过龙格-库塔方法，应用MATLAB 即可进行求解，结果如图17所示.

图17 安瓿内部压强随时间变化曲线Fig.17 Curve of internal pressure of the ampoule with time

图17 即为整个注射过程中安瓿内部停滞压强的变化曲线.由图可知，注射开始瞬间停滞压强较大，为28.2 MPa，并呈振荡衰减趋势，在0.06 s时刻压强稳定在11 MPa，符合Shergold 等人的研究规律：安瓿内部的停滞压力由瞬间高峰，然后振荡衰减［20］.由此可以认为此压强条件满足试验需求.

5.3.2 无针注射时间及速度结果分析

高速相机拍摄的有效图片张数为4 500，由式（4）即可得到整个注射过程的时间为0.106 s.以0.005 3 s为时间间隔，可以得到20个数据点.但采集结果显示，自0.090 1 s 时刻注射过程已不连续，如图18 所示，故以0 s 至0.084 8 s 为参考时间段，共16 个数据点.速度矢量方向如图19 所示，速度处理结果如图20所示.

图18 0.090 1 s时刻注射情况Fig.18 Injection at 0.090 1 s

图19 速度矢量图Fig.19 Vector of the velocity

由图20 可以得出：在同一时刻，由于空气的摩擦阻力，平均速度随着与微孔的水平间距增大而减小；在同一水平间距内，平均速度随着湍流充分发展而增大，在达到极值点后开始逐渐减小.同时在注射过程中，最大速度可以达到166.21 m/s.且在0～5 mm截面内，速度可以维持在150～165 m/s 范围内，在允许的试验误差内验证了优化方案的可行性.

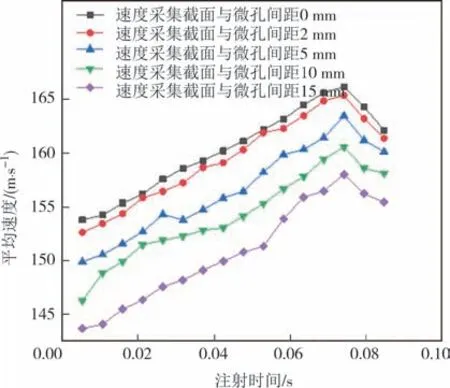
图20 平均速度随注射时间变化曲线Fig.20 Curves of average velocity with injection time

6 结论

提出了一种新型的大剂量多孔无针注射器，通过ANSYS Workbench 仿真平台得到了仿真结果.基于正交试验法对大剂量无针注射器的整体结构参数进行优化，且通过试验及动力学分析，验证了优化方案的可行性.依据以上研究得到了以下结论：

1）不同直径下的应力变化规律.根据拟合出的多项式，在安全系数为5 的条件下，得出对应入口压力13 MPa、14 MPa、15 MPa 下安瓿的最小直径分别为11.2 mm、11.9 mm、12.2 mm.

2）基于正交试验法对无针注射器多结构参数综合优化，得出最优结构方案：20°收缩角、1.4 的长径比、2 mm 的分布圆直径、4.05 mm 的收缩段长度和0.165 mm 的微孔直径，并且通过流固耦合验证了结构优化的合理性.

3）建立了大剂量无针注射器的动力学方程，通过龙格-库塔方法，得到了安瓿内部压强的数值解.结果显示整个注射过程中安瓿内部的压强基本满足实验需求，为无针注射试验提供了理论基础.

由无针注射试验得到了注射过程的基本规律：由于空气的摩擦阻力等原因，注射速度随着与微孔的水平间距增大而减小；同时随着湍流充分发展而增大，在达到极值点后开始逐渐减小.同时也可以得到注射过程中的最大速度出现在湍流的充分发展阶段，其值为166.21 m/s，且在距微孔0～5 mm 的截面内注射速度可以维持在150～165 m/s，在允许的试验误差内验证了优化方案的可行性.