基于SMC和最优电流矢量的无刷直流电机矢量控制

边真真 ，李风生

（1.天津航天中为数据系统科技有限公司 天津 300301；2.天津电气科学研究院有限公司 天津 300301）

0 引 言

无刷直流电机 BLDC 具有结构简单、惯性小、启动转矩大、制动效果好、调速范围广、效率高等优点，被广泛地应用于各类驱动控制系统［1-3］，如民用电器、工业控制、汽车、航空航天等多个领域。

传统的无刷直流电机一般采用比例积分（PI）控制、脉冲宽度调制（PWM）［4-6］方波调制策略，其优点是算法简单、易实现，缺点是输出转矩波动大、噪声大、对开关管器件影响大等。近年来，很多科研人员开始研究正弦波驱动电机的方法，如正弦波脉宽调制（ SPWM）、空间矢量脉宽调制（SVPWM）等。

为了克服运行时输出转矩波动大、稳态精度不高等问题，本文在传统 SVPWM 矢量控制的基础上提出一种基于滑模控制（SMC）和最优电流矢量相结合的控制算法，对速度调节器采用 SMC 控制，对 q 轴电流调节器采用最优电流矢量和 PI 控制。通过对仿真结果进行分析，证明所采用的控制算法可以有效抑制转矩波动、降低转速超调和提高稳态精度。

1 无刷直流电机数学模型

因无刷直流电机反电动势及其气隙磁场是梯形波、定子电流是方波，均属于非正弦控制，此时采用传统的交直轴坐标变换分析方法不再有效。采用经典的基尔霍夫电路定律、运动方程通过等效数学建模能够获得相对较为准确的控制结果。以两相导通星形三相六状态为例，直接利用无刷直流电机自身的各个状态变量来搭建 BLDC 数学模型。

为了方便分析，提出以下理想条件假设：①定子三相绕组对称，空间互差120°，参数相同；②不考虑电枢反应，电机气隙磁感应强度近似为方波；③不考虑涡流损耗、磁滞损耗；④定子铁芯齿槽对系统不产生影响。基于以上假设，数学模型［7-9］如下。

1.1 电压方程

1.2 转矩方程

电磁转矩通过绕组合成磁场和转子磁场相互作用产生，则：

1.3 运动方程

其中：B为阻尼系数（N•m•s/rad）；J为转动惯量（kg•m2）；LT为负载转矩（N•m）。

2 控制器设计

2.1 SMC滑模控制器

目前无刷直流电机速度调节普遍采用传统的PI比例积分控制，具有调节简单、参数调整方便等特点。而无刷直流电机作为一个非线性、强耦合多变量混合交叉控制系统，容易受内部（如物理参数发生变化等）及外部（如突然产生的扰动等）环境影响，进而使PI控制难以满足实际应用需求。

为了提高系统的调速质量，利用滑模控制对系统内、外未知干扰及其他不确定因素影响不敏感、响应速度快等优点，速度环调节器采用 SMC 滑模控制来替代 PI 控制。下面定义 BLDC 系统状态变量为：

参考式（2）、（3）、（4），定义状态方程如式（5）所示：

定义滑模面函数为：

为使系统具备较好的鲁棒性，采用趋近律方法可使运动过程更加平滑，故采用指数趋近律［10-12］：

对式（6）求导，结合式（5）、（7），可得d轴参考电流如式（8）所示：

其中：D、c、ε、q为待配系数。

因控制器包含积分项，可以削弱抖振及系统稳态误差。根据滑模稳态判定条件，易验证在控制器（公式8）控制下，系统渐进稳定。

2.2 最优电流矢量控制

控制系统调制策略采用 SVPWM 矢量控制，此时逆变桥处于三三导通模式。假设对换相和正常导通期间不予严格区分，使用平滑连续电流取代近似阶跃方波电流则能够从根源上消除因电流换相导致的转矩脉动[13]问题。

为了有效抑制换相过程中引起的转矩波动，q 轴电流环调节器采用最优电流矢量控制。结合式（2），注入的最优电流矢量应满足式（9）：

其中：常数k表示扇区号，其整数取值范围为k∈｛1，2，3，4，5，6｝；变量θe表示电角度；常数Ke表示电磁时间常数。

其中电角度θe和扇区号k之间的关系如表1所示。

表1 电角度和扇区号的关系Tab.1 Relationship between electrical angle and sector number

3 无刷直流电机控制系统建模仿真

采用控制系统框图如图1所示，主要涉及SMC滑模速度环模块、PI电流环模块、最优电流控制模块、Clark模块、Park模块、反Park模块、SVPWM 矢量模块、信号检测模块等。

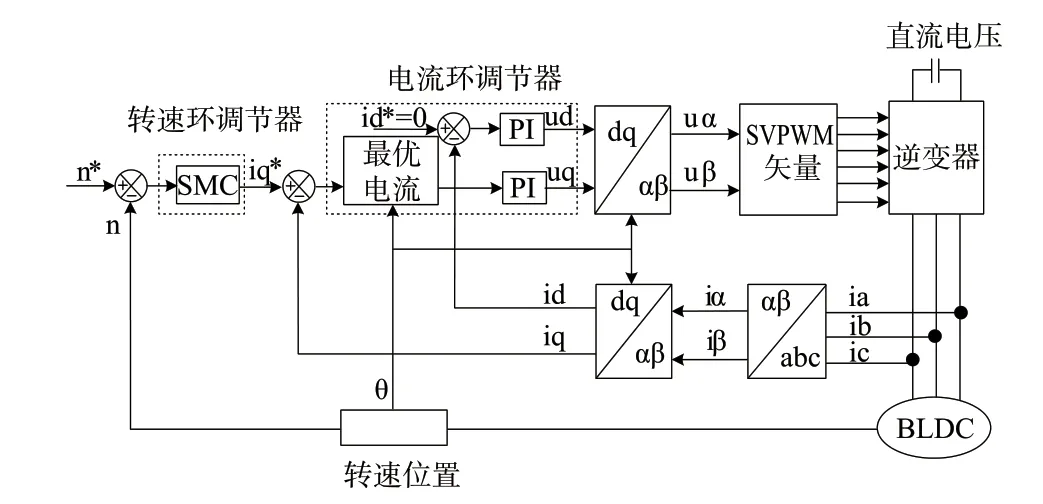
图1 基于SMC和最优电流矢量的SVPWM控制系统Fig.1 SVPWM control system based on SMC and optimal current vector

为验证所设计控制器的正确性，基于图1的控制策略，通过 matlab simulink 仿真环境进行建模。最终搭建的整体仿真模型图如图2所示。

图2 基于SMC和最优电流矢量的matlab仿真模型Fig.2 Matlab simulation model based on SMC and optimal current vector

根据式（8），搭建的指数型SMC控制器模型如图3所示。

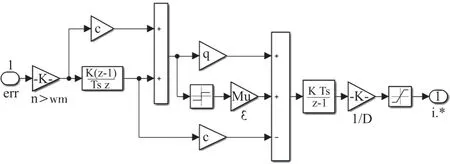
图3 指数型SMC控制器仿真模型Fig.3 Simulation model of exponential SMC controller

在图3中，err 输入信号为参考速度与输出反馈速度的偏差信号，其经过 SMC 控制，输出作为 q轴电流的参考信号。经过多次调节和优化，以下相关参 数 的 最 佳 取 值 分 别 为

4 仿真结果和分析

在仿真模型中，采用的 BLDC 无刷直流电机参数为：定子电阻R=3.05 Ω，定子电感L=17 mH，极对数P=5，磁链Ψ=0.077 Wb，转动惯量J=0.000 3 kg•m2。

仿真条件设置为：直流侧电压为U.μ=311 V，PWM开关频率f=10 kHz，仿真周期T=0.5 μs。采用变步长ode23tb算法，相对误差relative tolerance为0.001，仿真时间为0.5 s。

转速环调节器分别采用 SMC 控制和 PI 控制，其他条件设置一样，仿真结果如图4所示。仿真结果表明，相对于传统的 PI 控制，SMC 滑模控制具有超调小、动态响应时间短等优势。

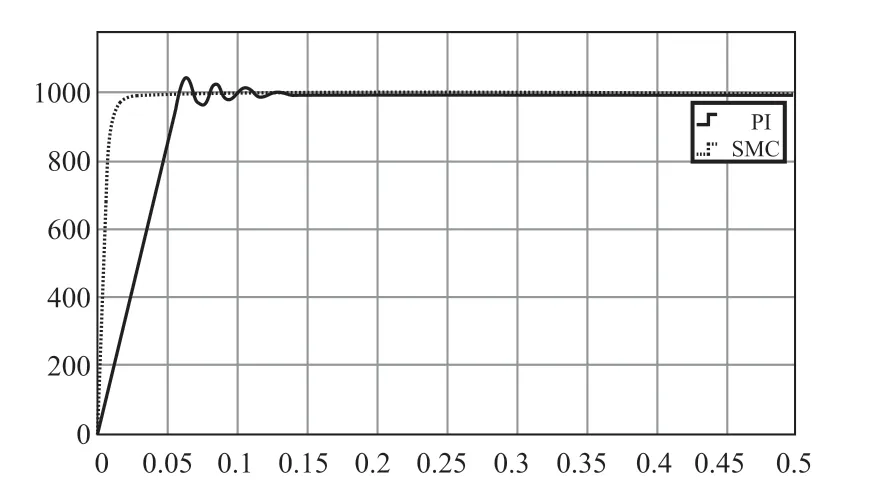
图4 输出转速波形Fig.4 Output speed waveform

转速环采用 SMC 控制，q 轴电流环分别采用传统矢量控制和增加最优电流矢量控制，其他条件设置一样，仿真结果如图5所示。该结果表明，相对于传统矢量控制，最优电流矢量控制能够有效抑制换相瞬间产生的脉动尖峰。

图5 输出转矩波形Fig.5 Output torque waveform

5 结 语

本文基于matlab simulink仿真软件，搭建了采用SVPWM 矢量控制的无刷直流电机仿真模型，其中转速环采用SMC控制，q 轴电流环注入最优电流矢量控制。从仿真结果可知，相对于传统的转速环PI及矢量控制，本文提出的新型控制算法可以有效降低无刷直流电机转速超调、抑制换相转矩脉动、提高动态响应能力和增加系统稳定性。