基于势能信息熵的黄土小流域地貌演化特征
赵卫东, 王淑琴, 田 剑, 季 斌, 马 雷
(合肥工业大学资源与环境工程学院,安徽 合肥 230009)
尽管早在20 世纪50—60 年代就有诸多地貌学者充分认识到把一般系统论应用到地貌学研究中的重要性,并在把该理论引入地貌学研究中做出了诸多有益尝试[1-3],但直到20 世纪80 年代初系统论才在地貌学研究中得到较广泛应用[4-6]。近年来,从系统论观点出发,对流域地貌进行研究已得到了广泛认可。励强等[7]提出了关于流域地貌的相关数学模型。马新中等[8]指出流域地貌系统是一个与外界不断进行物质和能量交换的典型开放自然系统。
熵的物理意义最早是用于表征热力学系统中体系混乱的程度。Leopold 等[9]最早提出了地貌熵的概念,但由于地貌熵难以进行定量计算,因此并没有得到更加广泛和深入的研究。近年来,随着数字高程模型(DEM)技术的快速发展,Zhao 等[10]通过类比热力学熵,提出了流域地貌熵的概念及其数学模型,并成功应用于室内人工降雨条件下均质黄土流域地貌演化过程研究。
Shannon[11]最 早 提 出 了 信 息 熵 的 概 念。Neumann[12]和Higashi 等[13]对信息熵及其测量方法开展了进一步研究。艾南山[14]基于Davis和Strahler地貌发育模型及信息熵的概念,提出了地貌信息熵的概念及其计算公式。岳天祥等[15]在地貌信息熵的基础上进一步提出地貌信息超熵的概念。由于地貌信息熵包含了地貌发育信息,因此地貌信息熵在冲沟沟头活跃度和泥石流危险性评价等方面得到了较广泛应用[16-17]。陈楠等将信息熵应用于不同尺度DEM 的信息容量变化研究[18-21]。姜琼[22]基于系统论和信息熵的原理提出了势能信息熵的概念及其在均质黄土流域地貌系统中的数学模型,并得出了势能信息熵在一定程度上可以反映流域地貌系统内部的物质侵蚀和堆积情况等初步结论。赵卫东等[23]基于势能信息熵对黄土小流域沟谷网络演化的变化特征进行研究,结果表明该流域势能信息熵的变化特征和沟谷网络的有序化程度高度一致。但上述结论仅基于室内人工降雨模拟实验的均质黄土地貌演化过程得出,是否同样适用于野外黄土高原真实小流域有待进一步深入研究。为此,本文基于系统论的观点和方法,构建多岩土层黄土小流域地貌系统及其势能信息熵的数学模型,并以黄土高原辛店沟小流域为典型样区,对辛店沟小流域地貌系统的势能信息熵及其熵变规律进行研究,并据此探索该流域的地貌演化特征,为进一步揭示辛店沟小流域地貌演化机制和土壤侵蚀机理提供重要技术支撑。
1 研究区概况
本文以黄土高原辛店沟小流域(图1)为研究区,开展多岩土层黄土小流域地貌演化特征研究。该流域位于陕西省榆林市绥德县无定河左岸的辛店沟,地理范围为110°16′~110°17′E、37°29′~37°31′N,属于黄土丘陵沟壑区第一副区,地表侵蚀较严重[24]。研究区气候干燥,属半干旱区温带大陆性气候,降水的年际变化大,多集中在汛期的6—9 月[25]。土壤质地疏松,以黄绵土为主,主要分布于地形平缓或植被较好区域[26]。

图1 辛店沟小流域地理位置Fig.1 Geographic location of Xindiangou small watershed
2 数据与方法
2.1 数据来源与处理
为研究辛店沟小流域地貌演化过程,本文收集了该流域不同时期的5 期DEM 数据,如表1 所示。利用ArcGIS 软件将上述5 期DEM 数据统一投影至WGS_1984_UTM 投影坐标系,并将所有数据重采样为90 m分辨率。

表1 2000—2019年辛店沟小流域DEM数据Tab.1 DEM data of Xindiangou small watershed from 2000 to 2019
为查明辛店沟小流域内部岩土层的空间分布及其密度差异,作者于2021 年8 月对该小流域开展了野外实地调查和岩土密度的取样测试(图2)。该采样点位于辛店沟小流域主沟道的中下游,从该图中可以看出,流域下部有明显的岩土分层情况,垂直方向从下往上依次为砂岩、页岩和黄土。在岩土取样点1_9(表2)测得砂岩和页岩的密度分别为2.80 g·cm-3和2.21 g·cm-3。整个小流域内部各取样点黄土密度如表2所示,从表中可以看出,整个研究区内部黄土密度差异较小。辛店沟小流域黄土密度取表格中27 个取样点黄土密度的平均值,为1.32 g·cm-3。
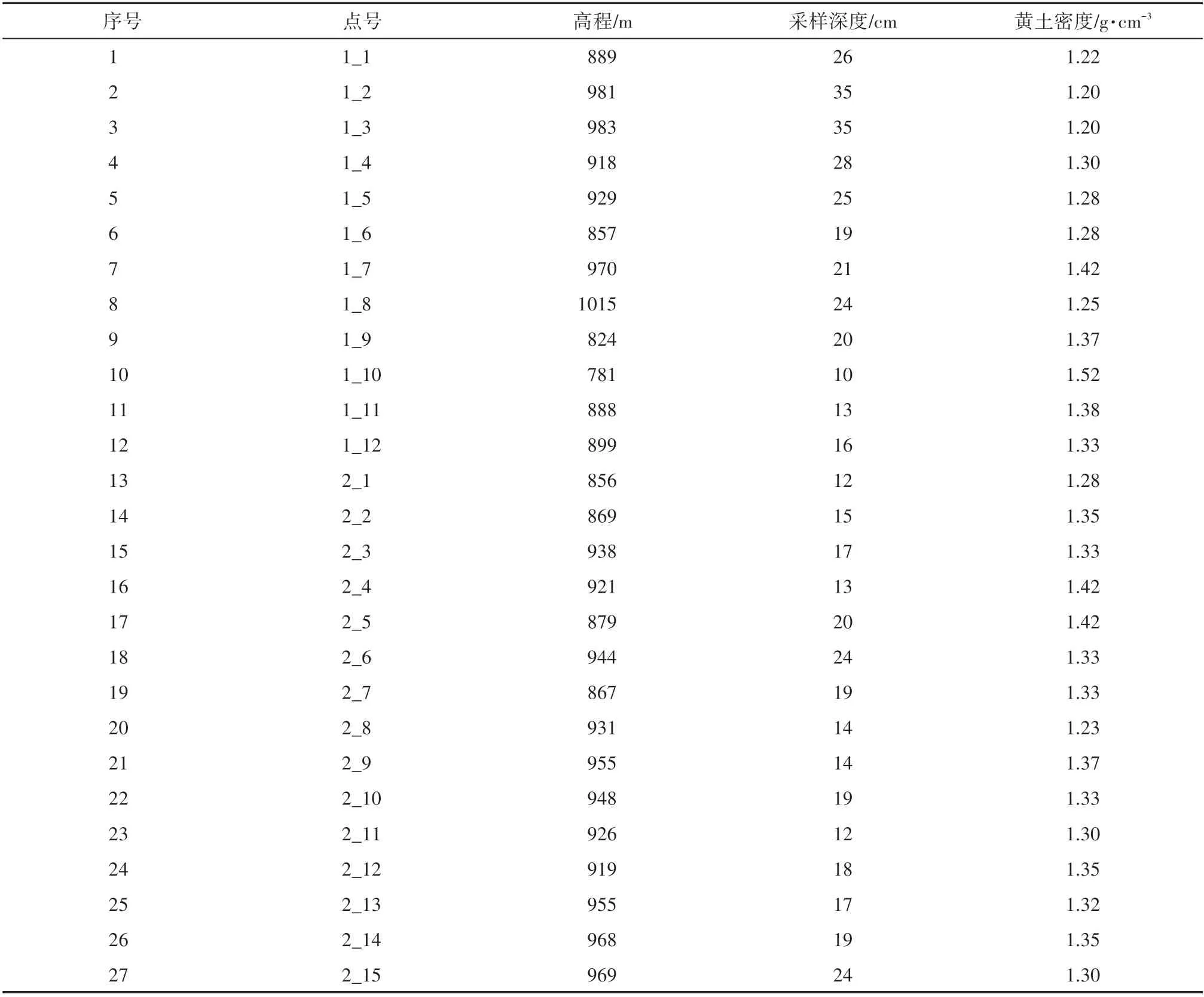
表2 辛店沟小流域黄土密度Tab.2 Loess density in Xindiangou small watershed

图2 野外岩土调查和黄土密度测量取样Fig.2 Field geotechnical investigation and sampling of loess density measurement
2.2 多岩土层黄土小流域地貌系统概念模型构建
黄土高原小流域地貌系统是一个与外界不断进行物质和能量交换的典型开放自然系统[8]。一个完整的流域地貌系统一般拥有四周、上部和底部边界。为构建多岩土层黄土小流域地貌系统的概念模型,首先必须确定该系统的边界。本文以辛店沟小流域地貌系统为例,构建多岩土层小流域地貌系统的概念模型。根据辛店沟小流域野外实地调查结果,该流域地貌系统的最底部为砂岩层,上覆页岩层,顶部为黄土层。因此,本文把辛店沟小流域地貌系统的上部边界确定为整个辛店沟小流域范围内的地形表面,系统四周的侧向边界为沿小流域分水岭构建的垂直于水平面的垂直面,系统底部边界为该小流域出口附近高程最低点所在的水平面。该水平面也是辛店沟小流域地貌系统的势能计算基准面。根据上述岩土层分布及系统边界,构建出辛店沟小流域的流域地貌系统的概念模型,如图3所示。

图3 辛店沟小流域地貌系统的概念模型Fig.3 Conceptual model of the geomorphic system of Xindi‐angou small watershed
2.3 多岩土层流域地貌系统的势能信息熵数学模型构建
2.3.1 多岩土层流域地貌系统的剖分流域地貌系统的势能是指以流域底部边界为势能计算基准面,计算出的整个流域地貌系统边界范围内的岩土体所具有的总势能。为了计算出整个多岩土层流域地貌系统的势能和势能信息熵,需要对整个流域地貌系统进行平面剖分和垂向分层。首先,利用DEM正方格网剖分技术,对流域地貌系统进行平面剖分,把整个流域在平面上剖分为m×n个正方格网单元格。剖分单元格的大小和该流域DEM 数据的单元格一致。由于势能与岩土体的密度紧密相关,因此,为了准确计算具有不同密度岩土层的势能,需要根据岩土层密度的不同,对整个流域地貌系统在垂向上进行分层。至此,完成了整个多岩土层流域地貌系统的三维剖分工作,使其形成一个包含m×n个基本单元体的三维立体剖分体,每个单元体在垂向上可以包含不同密度的岩层或土层。通过计算出每一个单元体的势能并进行累加就可以计算出整个流域地貌系统的总势能。根据上述剖分方法,考虑到辛店沟小流域中出露的基岩和黄土密度相对均匀,无需对岩土层内部进行进一步垂向剖分。因此,该系统在垂向上可剖分为砂岩、页岩和黄土3个分层。
2.3.2 多岩土层势能信息熵数学模型构建姜琼[22]于2019年提出了流域地貌系统的势能信息熵概念,并成功构建了均质黄土小流域地貌系统的势能信息熵数学模型。该模型被用于室内人工降雨条件下的均质黄土小流域地貌系统的地貌演化研究,取得了较好的研究成果。但该模型不适用于非均质多岩土层流域地貌系统。势能(Ep)的计算公式如下:
式中:g为重力加速度(m·s-2);ρ为室内均质黄土密度(g·cm-3);d为单元格尺寸(mm);h为每个计算单元体相对于流域地貌系统出口处最低高程的高度(mm)。
为此,本文基于前述多岩土层流域地貌系统的剖分单元体和势能信息熵概念,按照以下步骤构建多岩土层流域地貌系统的势能信息熵数学模型。
首先,根据野外实地调查测量的基岩倾向、倾角和厚度等相关信息,计算出该多岩土层流域地貌系统内部第i行第j列剖分单元体的基岩高度(Hi,j)(起算点为流域地貌系统的底部边界),计算公式如下:
式中:α为流域地貌系统中基岩的倾向(°);β为基岩的倾角(°);X0、Y0为基岩取样点的经度、纬度(°);Z0为基岩取样点的高程(m);H0为小流域出口处最低点的高程(m);X、Y为第i行第j列剖分单元格左下角的经纬度坐标(°)。
其次,多岩土层流域地貌系统的势能(Eq),计算公式如下:
式中:g为重力加速度(m·s-2);ρk为岩层密度(g·cm-3);d为单元格尺寸(m);Hi,j,k为第i行第j列剖分单元格的第k层岩层高度(m);Hi,j,k-1为第i行第j列剖分单元格的第k-1 层岩层高度(m);k为剖分单元格中岩土层层数;m为单元格行数;n为单元格列数。
姜琼[22]的研究表明,流域地貌系统的势能分级数与势能信息熵的大小密切相关,随着势能分级数不断增加,势能信息熵最终会逐步趋于一个稳定值,此时的势能分级数为最佳势能分级数。利用式(1)对每个单元体的势能值进行计算,并根据势能值大小的不同将其等间距分为若干势能等级。最后,对小流域地貌系统内部的势能信息熵(Ha)进行计算[22],计算公式如下:
式中:p(i)为单元体i所属的势能等级在该小流域所有的势能等级中出现的概率;m为单元格行数;n为单元格列数。
利用上述多岩土层流域地貌系统的势能信息熵数学模型,以辛店沟小流域地貌系统为例,按照以下步骤计算出其势能信息熵。首先,根据野外实地调查结果,辛店沟小流域底部砂岩层和页岩层倾向和倾角相同,岩层厚度均匀,且其厚度已经测出。利用5 期辛店沟小流域DEM 数据和式(2)及式(5)可计算出每期DEM的流域地貌系统势能(Et)。
式中:g 为重力加速度(m·s-2);ρ1为砂岩密度(g·cm-3);ρ2为页岩密度(g·cm-3);ρ3为黄土密度(g·cm-3);d为单元格尺寸(m);Hi,j为第i行第j列单元体的砂岩厚度(m);bi,j为第i行第j列单元体的顶部界面相对于流域地貌系统出口最低点的高度(m);H2为页岩厚度(m);m为单元格行数;n为单元格列数。
其次,利用式(4)计算出辛店沟小流域地貌系统内部的势能信息熵。为了确定该流域地貌系统的最佳势能分级数,分别计算出每期数据在不同势能分级数下对应的势能信息熵,结果如图4所示。

图4 辛店沟小流域势能信息熵随分级数变化Fig.4 Change of potential energy information entropy varying with classification number in Xindiangou small watershed
从图4中可以看出,当势能分级数不断增大时,势能信息熵与势能分级数的联系逐渐削弱,最后趋于一个常数。因此,为了准确计算出该流域地貌系统内部的势能信息熵,需要找到一个最佳分级数,即对势能信息熵计算结果几乎没有影响的分级数。本文根据文献[22]取势能信息熵的变化率为负万分之一时对应的分级数为最佳分级数,经计算最佳分级数为500级。即当分级数为500级时,5期DEM数据对应的流域地貌系统的势能信息熵的变化率很小,可以忽略不计,此时可获得小流域地貌系统唯一稳定的势能信息熵。因此,本文的计算均以500级作为最佳势能分级数。
3 结果与分析
3.1 势能信息熵的地貌侵蚀特征
势能信息熵主要用于表示流域地貌系统中势能在空间分布上的混乱程度,这与热力学熵代表热力系统中分子混乱程度的特性类似[22]。此外,势能信息熵的变化能反映流域地貌系统内部势能的变化,这与热力学熵的熵变情况代表热力系统中分子运动能量变化的特性类似[27]。因此,势能信息熵的变化能在很大程度上反映流域地貌系统内部黄土侵蚀特征和势能空间分布特征。姜琼[22]利用势能信息熵对室内人工降雨条件下均质黄土小流域(以下简称“室内小流域”)的黄土侵蚀特征进行了初步研究,结果表明势能信息熵的熵减过程能够有效反映黄土小流域的侵蚀过程。为进一步验证该结论是否适用于野外真实多岩土层黄土小流域,以辛店沟小流域地貌系统为例,研究其势能信息熵与黄土侵蚀之间的关系。
田剑等[28]的研究证明沟壑密度和土壤侵蚀强度存在显著的正相关,随着沟壑密度不断增大,土壤侵蚀逐渐加强。因此,本文拟通过研究黄土小流域地貌系统的势能信息熵与沟壑密度之间的相关关系,间接验证势能信息熵与黄土侵蚀之间的关系。利用前述方法计算出辛店沟小流域5 期DEM的势能信息熵,然后采用南学良等的沟谷网络密度二阶导函数法确定该小流域的汇流累积量阈值为12[29],据此提取5 期DEM 的沟谷网络并计算出其沟壑密度,结果如图5所示。
从图5a 中可以看出,5 期DEM 的势能信息熵均为负熵,且总体上呈不断减小态势。在整个地貌演化过程中,势能信息熵最小值为-1.187,最大值为-1.096。从2000 年到2019 年势能信息熵减少了8.30%。与之相对应,沟壑密度总体上呈小幅增加的态势,最小值为1.771 km·km-2,最大值为1.896 km·km-2。从2000 年到2019 年沟壑密度仅小幅增加7.06%。这表明,辛店沟小流域地貌系统的演化过程是一个势能信息熵不断减小的过程,同时也是该系统内部的沟壑密度小幅增大、黄土侵蚀小幅增强的过程。对势能信息熵和沟壑密度进行多项式拟合,结果如图5b 所示。从该图可以看出,沟壑密度与势能信息熵之间具有良好的三次多项式函数关系。利用该拟合公式,可通过计算小流域地貌系统的势能信息熵来大致估算其沟壑密度。这表明辛店沟小流域势能信息熵的熵减过程是该流域地貌侵蚀小幅增强的过程,该结论和姜琼[22]的结论一致,进一步证实了该结论的正确性。

图5 辛店沟小流域势能信息熵与沟壑密度变化及拟合曲线Fig.5 Variation and fitting curve of potential energy information entropy and gully density in Xindiangou small watershed
3.2 势能信息熵的地貌发育特征
姜琼[22]的研究表明,在室内人工降雨模拟实验条件下,均质黄土小流域的势能信息熵能够很好地指示黄土小流域的地貌发育阶段。为进一步验证该结论是否适用于野外非均质多岩土层黄土小流域地貌系统,本文利用势能信息熵对辛店沟黄土小流域地貌系统的地貌发育过程进行研究。首先,采用起伏比法计算5 期DEM 的Strahler 面积高程积分(Hypsometric index,HI)。起伏比法是Pike 等[30]经过数学公式推导得出的估算HI 的方法,计算公式如下:
本文利用ArcGIS 软件提取不同时期DEM 的最大值、最小值及平均值,再利用式(6)求取HI[31],计算结果如表3所示。
从表3 中可以看出,HI 随着地貌演化年份的增加呈现不断减小趋势,2000 年HI 最大,为0.534,2019年HI最小,为0.485,2000—2019年地貌演化过程中,HI 减小了9.18%。5 期DEM 的HI 均位于0.4~0.6 之间,因此,从2000—2019 年辛店沟小流域地貌发育阶段均为壮年期。

表3 5期DEM的Strahler面积高程积分Tab.3 Strahler hypsometric index of 5 periods’DEM
为了更直观对比室内小流域与野外辛店沟小流域在侵蚀过程中的HI 和势能信息熵的动态变化特征,本文绘制了2 个小流域的势能信息熵与HI 变化曲线,如图6所示。
姜琼[22]的研究表明,在地貌发育的幼年期势能信息熵不断减小,在壮年期势能信息熵不断增大(图6a)。然而,辛店沟小流域的地貌发育过程表明,在其地貌发育的壮年期势能信息熵却不断减小,与室内小流域势能信息熵变化不一致。为此,本文结合戴维斯的地貌侵蚀循环理论[32]、势能信息熵的概念和室内小流域、辛店沟小流域的势能信息熵变化特征,对产生该差异的原因进行分析。假设存在一个地表完全水平的流域地貌系统,在地貌开始发育演化时,此时处于流域地貌发育阶段的幼年期最初阶段,该系统内部任意2个点的高程都相等,所有剖分单元格的势能均属于同一个级别。根据势能信息熵的定义,此时该流域的势能信息熵应为0,即任意一个单元格的势能等级都有100%的概率会落入该唯一势能级别中。随着地貌不断演化,流域内部地表由于受到降雨等侵蚀,开始逐步降低并形成沟谷网络,逐步形成多个不同的势能等级,使得每一个单元格的势能等级的概率均小于1,这表明随着地貌的不断侵蚀,势能信息熵将不断减小。但根据戴维斯的地貌循环理论,该流域地貌最终的地貌演化目标是形成夷平面或准平原,也就是最终该流域地貌系统的地表将再次变为水平或近似水平,此时势能信息熵将再次变为0。本文把上述流域地貌完整演化过程中形成的势能信息熵变化曲线称为该流域的标准势能信息熵变化曲线。根据上述原理和室内小流域及辛店沟小流域势能信息熵的变化情况,分别推测出室内小流域和野外小流域地貌演化的标准势能信息熵和HI变化曲线,如图7所示。

图6 势能信息熵和面积高程积分随地貌演化时间的变化Fig.6 Variations of potential energy information entropy and hypsometric index with geomorphic evolution time
从图7 中可以看出,室内小流域的势能信息熵在GR 段不断减小,在RH 段不断增加,且R 点的HI为0.59,非常接近幼年期和壮年期的分界值0.6。此外,辛店沟小流域的势能信息熵在EF 段不断减小,根据前述分析,在该流域地貌演化结束时,辛店沟小流域的势能信息熵应趋近于0。因此,本文大胆推测辛店沟小流域的势能信息熵可能会在壮年期和老年期分界点Q 处发生转折,在QL 段不断增加,并最终趋近于0。同理,进一步推测室内小流域的势能信息熵也可能会在壮年期和老年期分界点T处发生转折,在TL 段不断增加,并最终趋近于0。此外,由于沿FE方向辛店沟小流域的势能信息熵不断增加,而室内小流域沿RH 方向势能信息熵也是增加的,由此推测与之对应沿NP 方向的势能信息熵也应增加,从而形成拐点P,同理,在室内小流域曲线上会形成拐点S。最终,推测室内和野外小流域地貌系统在其完整的地貌演化过程中均将形成类似W 型的势能信息熵变化曲线,这表明势能信息熵能够很好地指示流域地貌幼年期、壮年期和老年期的地貌发育分界点,较好地指示流域地貌发育的阶段。
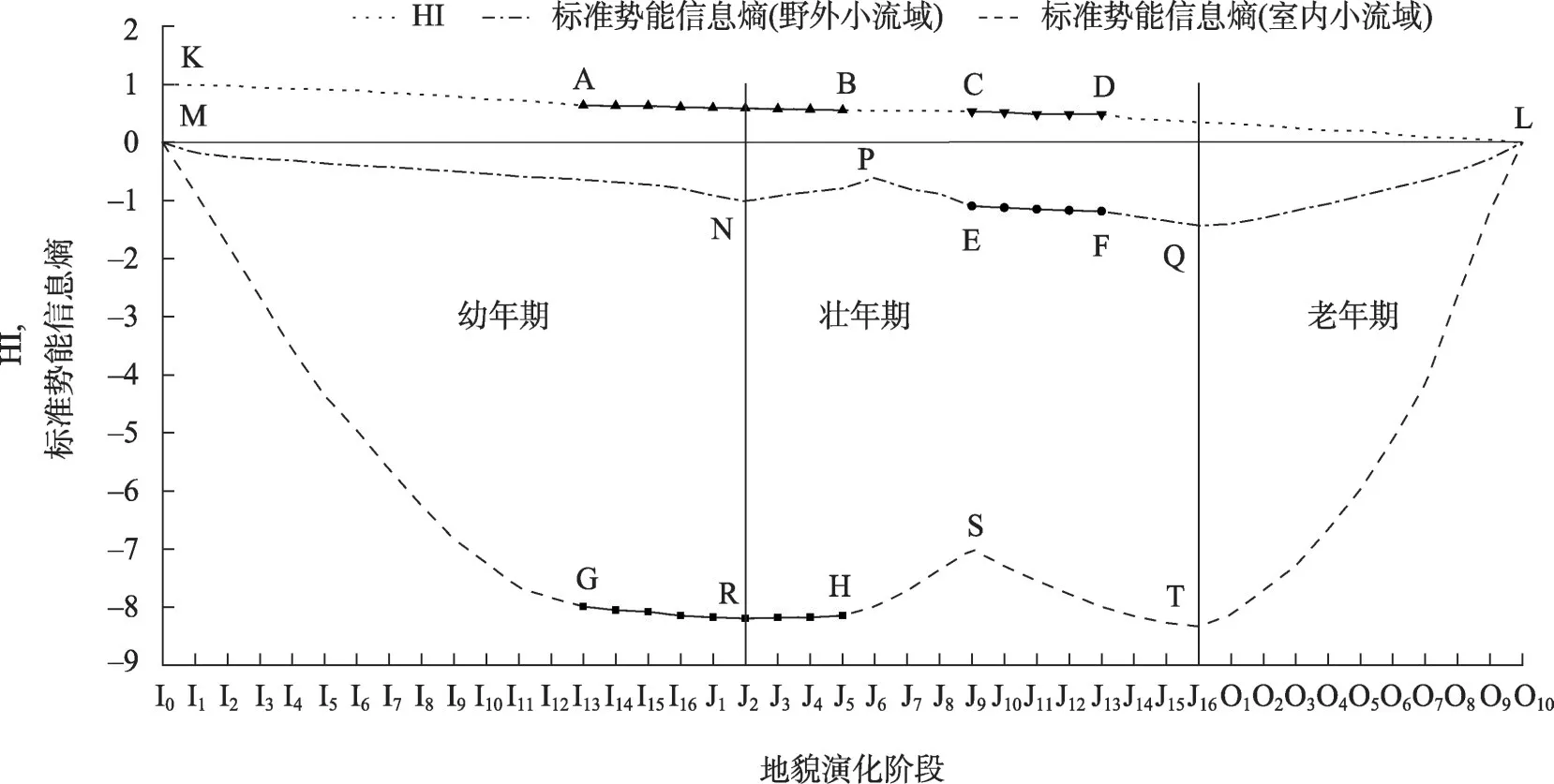
图7 室内和室外小流域的标准势能信息熵和面积高程积分变化Fig.7 Variations of the standard potential energy information entropy and hypsometric index of indoor and outdoor watersheds
4 讨论
黄土高原流域地貌系统的地貌形态、侵蚀和发育特征由于受到流域内部地层岩性、植被、降雨和人类活动等诸多因素影响,使其演化特征十分复杂。为此,本文充分考虑辛店沟小流域的地层岩性和岩土层密度等因素,通过构建辛店沟小流域地貌系统及其势能信息熵的数学模型,从流域地貌系统的势能信息熵这一独特视角对黄土小流域的地貌演化的综合特征进行探索。上述研究结果表明,本文构建的辛店沟多岩土层流域地貌系统及其势能信息熵能够有效对辛店沟小流域进行数值模拟。野外自然条件下辛店沟小流域的地貌演化过程是其势能信息熵的熵减过程,该结论与姜琼[22]在室内人工降雨模拟试验条件下的均质黄土地貌演化过程研究中得出的结论一致。这说明势能信息熵的熵减过程能够有效反映黄土小流域地貌不断侵蚀的过程。此外,本文提出的利用标准势能信息熵曲线对流域地貌发育阶段进行划分的方法,尽管还有待于后续开展更深入研究进行验证,为流域地貌发育阶段的精细划分提供了一条新的途径,非常适合处于不同发育阶段的流域地貌对比研究。未来我们将选取更多的处于幼年期、壮年期和老年期等不同发育阶段的黄土小流域进行深入研究,对标准势能熵曲线形态、曲线拐点的地貌演化意义等进行验证。
5 结论
(1)本文基于前人研究及辛店沟小流域野外实地考察获取的数据,成功构建了野外多岩土层黄土小流域地貌系统的概念模型及其势能信息熵的数学模型。该模型能够有效对辛店沟小流域进行数值模拟,是对现有均质单一黄土层的势能信息熵数学模型的扩展,可在非均质多岩土层流域地貌系统中使用,具有更广泛适用性。
(2)研究结果表明,以黄土侵蚀作用为主的辛店沟小流域从2000—2019 年的地貌演化过程是其势能信息熵的熵减过程和黄土地貌不断侵蚀的过程。
(3)辛店沟小流域的势能信息熵可能能够指示该流域地貌发育的壮年期和老年期分界点,室内小流域的势能信息熵能够较好指示幼年期和壮年期分界点。为此,本文推测:黄土流域地貌系统在其完整的地貌演化过程中将形成类似W 型的标准势能信息熵变化曲线,该曲线能较好指示流域地貌幼年期、壮年期和老年期的地貌发育分界点,可为流域地貌发育阶段的精细划分提供一条新途径。
——《势能》

