经济波动、网络关联与银行业系统性风险监管

宋凌峰 肖雅慧

(武汉大学 经济与管理学院，湖北 武汉 430072)

一、引言

随着中国经济进入新常态，经济下行压力增加，系统性金融风险持续累积。自党的十九大报告指出“健全金融监管体系，守住不发生系统性金融风险的底线”以来，防范化解系统性金融风险已经成为金融监管当局的重要政策目标。2021年12月31日，中国人民银行发布《宏观审慎政策指引(试行)》，明确提出系统性金融风险主要来源于时间和结构两个维度，从时间维度看，系统性金融风险由金融活动的一致行为引发，随着时间的累积呈现出风险顺周期的自我强化和自我放大特征；从结构维度看，系统性金融风险由特定机构或市场的不稳定引发，并通过风险关联途径扩散，导致风险跨机构、跨部门、跨市场、跨境传染。本文根据结构维度将系统性金融风险来源进一步细化为机构内部脆弱性、机构间网络关联和外部经济波动三个部分[1]，并结合时间维度分析不同风险来源的时变特征。其中，机构内部脆弱性对应于微观机构个体所引发的风险，与机构规模、资产负债状况等有关；机构间网络关联对应于中观行业内机构之间的风险传染，单个机构经过业务往来、交叉持股、共同持有资产等网络关联渠道，将风险进行扩散和传染；外部经济波动对应于宏观经济环境所引发的风险，主要表现为风险的顺周期性。机构自身脆弱性以个体风险为主，机构间网络关联和外部经济波动是形成系统性金融风险隐患的关键来源，因此更加需要关注机构间网络关联和外部经济波动对系统性金融风险的影响。

银行业是中国金融系统的核心，系统性金融风险管理的主要任务之一是银行业系统性风险管理，本文将银行业系统性风险作为研究对象，将其划分为银行内部脆弱性、银行间网络关联和外部经济波动三个风险来源，其中银行内部脆弱性风险来源于规模[2-3]、杠杆率[4]、非核心负债[5]、收入多样化[6]等；银行间网络关联风险来源于银行资产负债表关联，包括银行间市场的同业拆借、同业存放等直接业务关联[7-8]、以及持有共同资产的间接业务关联[9-10]；外部经济波动风险来源于经济周期、经济冲击引起市场上风险资产的波动[11-14]。同时，从银行个体角度来看，银行业系统性风险的微观基础是单个银行的风险演变，我国银行业体系主要包括大型国有银行和中小型银行两种类型，二者在资产规模、业务模式、组织结构等方面存在显著差异，所以需要进一步区分银行业系统性风险的不同来源与不同类型银行之间的关系。但现有文献将经济波动看作风险的外生冲击因素，主要分析外生经济冲击对网络关联和系统性风险的影响，而忽略了系统性风险本身已包含外部经济波动的影响，也没有将系统性风险来源与个体来源相结合，缺乏对系统性风险来源微观基础的相关研究。

因此，本文将银行业系统性风险分解为银行内部脆弱性、银行间网络关联和外部经济波动三个部分，重点研究银行间网络关联和外部经济波动对银行业系统性风险的影响，同时分析银行业系统性风险的微观基础，研究不同风险来源受不同类型银行的影响程度。本文的理论创新价值体现在：基于经济波动影响内生于银行业系统性风险的视角，量化系统性风险中银行间网络关联、经济波动的影响，并分析不同银行个体对系统性风险不同来源的主导作用。本文的研究对于维护金融稳定和实施针对性的宏观审慎监管措施具有重要的现实意义。

二、文献综述

(一)经济波动、网络关联对系统性风险的影响

现有研究在分析经济波动、网络关联对银行业系统性风险的影响时，主要研究思路是首先通过构建银行间网络度量银行业系统性风险，然后将经济波动作为外生冲击因素，进而分析经济波动对网络关联和系统性风险的影响。在构建银行间网络以度量银行业系统性风险时，主要采用以下两种方法，一是根据银行间资金和业务往来数据构建网络[15-16]，风险通过银行同业拆借、银行共同持有资产、银行间支付结算等渠道实现传染和扩散；二是根据尾部风险指标△CoVaR测度银行两两之间的风险溢出效应，从而构建银行间风险传染网络[17-21]。

在构建银行间网络度量银行业系统性风险基础之上，学者们从不同角度刻画经济波动状况，从而研究经济波动对网络关联和系统性风险的影响。主要有以下几种观点：一是经济波动会带来资产投资风险的变化，从而影响平均储蓄量、储蓄的波动幅度、投资的收益率、投资回收期、投存比、存款准备金率以及储蓄利率等指标，经银行网络关联影响银行业系统性风险水平[15-16,22]；二是经济波动会带来经济政策的不确定性，经济政策不确定性的提高会加剧风险传染性[19]，在网络关联性更大的样本中，政策不确定性对银行业系统性风险的正向作用更加明显[18]；三是宏观经济状况直接影响银行的风险溢出效应，2015年股灾期间资本市场的波动导致各银行对外风险溢出增加，银行间关联性增强，银行业系统性风险上升[17,20-21]。

(二)系统性风险与银行差异化监管

国内外关于银行业系统性风险的个体来源进行了深入研究，提出开展银行差异化监管的建议。主要集中于以下三类观点：第一类观点从银行规模角度出发，认为银行的规模越大，其引发的系统性风险越大[23-24]，建议根据规模制定差异化的资本监管要求。第二类观点从银行间网络结构角度出发，认为处于网络中心地位的银行与其他银行的联系最为紧密，属于系统性重要银行，对银行业系统性风险贡献最大[8,21,25-26]，建议对核心银行和外围银行、主要系统重要性银行与非主要系统重要性银行实行差异化监管。第三类观点是从银行的同群效应角度出发，认为虽然单个中小银行违约造成的银行业系统性风险有限，但是中小银行之间存在同群效应，中小银行的联合倒闭所造成的系统性风险后果不容忽视[27-28]，建议对中小银行进行全局监管，例如设计合理的银行自救安排机制，弱化其被政府救助的预期，进而降低集体道德风险。

(三)文献述评

通过文献整理可以发现，在经济波动、网络关联对银行业系统性风险的影响研究方面，学者们都发现银行间网络关联是银行业系统性风险的重要来源，而且经济波动对网络关联和系统性风险都产生显著影响，但现有文献将经济波动看作风险的外生冲击因素，而忽略了系统性风险本身已包含外部经济波动的影响，也没有考虑经济波动的区制转移特征，缺乏关于经济状态和银行业系统性风险关系的讨论；在系统性风险与银行差异化监管方面，学者们从银行个体特征角度分析了不同差异化监管措施，但是这些研究没有将系统性风险来源与个体来源相结合，没有进一步明确个体造成的是何种类型的系统性风险，缺乏更加细致的研究。

在系统性风险度量方法中，网络分析法和尾部度量法局限于对网络关联的刻画，缺乏对经济波动因素的考量，而或有权益分析法(Contingent Claims Analysis，CCA)的核心思想是把权益市值看作以资产为标的、债务账面价值为执行价格的欧式看涨期权价值[29-31]，通过权益市值反推出资产市值，将需要偿还的债务作为违约点，当资产市值低于违约点时，违约距离下降，银行业系统性风险上升。由此可以看出，CCA模型度量的系统性风险受到违约点和资产市值变化的直接影响，其中违约点反映的是银行资产负债状况，属于内部脆弱性风险，而资产市值变化与经济波动密切相关，反映了外部经济波动的影响，因此违约距离是一个叠加了内部脆弱性和外部经济波动影响的混合性风险指标[32]。但是CCA模型的局限性在于对银行间的风险关联考虑不足，Gray和Jobst(2009)[33]拓展了CCA分析框架，通过刻画银行间违约风险相依结构反映机构间关联，测量所有银行的联合违约风险作为系统性风险指标，被称为系统或有权益分析(Systemic Contingent Claims Analysis，SCCA)。SCCA模型度量的系统性风险是将银行内部脆弱性、银行间网络关联和外部经济波动同时考虑其中的风险指标，为进一步研究内生性的经济波动、网络关联对系统性风险的影响提供了可能。

因此，本文采用SCCA模型度量中国银行业系统性风险，并考虑经济波动的区制转移特征，将SCCA模型与马尔科夫区制转移模型相结合，将银行业系统性风险分解为银行内部脆弱性、银行间网络关联和外部经济波动三个部分，重点研究银行间网络关联和外部经济波动对银行业系统性风险的影响，并把系统性风险来源与个体来源相结合，为制定差异化监管政策提供建议。

本文的创新点主要体现在以下两个方面：一是基于经济波动影响内生于银行业系统性风险的视角，并考虑经济状态转移特征，将SCCA模型与马尔科夫区制转移模型相结合，对系统性风险进行分解，量化系统性风险中银行间网络关联、经济波动的影响，讨论不同风险来源的贡献度及其相互关系；二是结合我国银行业体系的特殊结构，从大型国有银行和中小型银行两类银行的异质性角度，分析不同银行个体对系统性风险不同来源的主导作用，由此提出差异化监管的政策建议。

三、理论分析与模型构建

(一)理论分析

按照宏观、中观、微观三个层次对银行业系统性风险来源进行解析，其中银行业系统性风险的宏观来源是经济波动，经济波动通过利率渠道和股票市场渠道对系统性风险产生影响，在利率渠道上，经济形势影响实体投资收益，利率也会随之变化，影响银行资金的获取成本，带来银行风险抵御能力变化，从而影响系统性风险水平；在股票市场渠道上，经济波动导致上市银行股票市值和股票收益率波动，从而影响系统性风险水平。银行业系统性风险的中观来源是银行间网络关联，银行间通过同业业务往来、共同持有资产等方式构成风险传染网络，网络具有风险承担和风险溢出的功能，当单个非系统重要性银行风险增加时，造成较小的冲击，网络能够承担部分风险，系统性风险变化较小；当系统重要性银行风险增加时，风险通过网络传导影响与该银行密切联系的其他银行风险，实现风险溢出，加剧系统性风险恶化。银行业系统性风险的微观来源是银行自身资产负债表状况，反映内部脆弱性风险，当银行出现经营不善的情况，资产与负债在风险、收益和期限等方面不匹配，银行内部资金周转困难，也会导致系统性风险的上升。

而且，经济波动、网络关联和内部脆弱性对银行业系统性风险的影响并不是孤立存在。一方面，网络关联和内部脆弱性同属于银行业内部的风险因素，二者存在相互转化的关系，单个银行可以通过银行网络将自身脆弱性风险转移至其他银行，此时会降低银行内部脆弱性风险水平，但也显著增强了银行网络的关联性，增加网络关联对系统性风险的影响[21]；另一方面，经济波动对系统性风险的影响程度与内部脆弱性有关，当银行内部脆弱性较大时，系统性风险对外部经济波动的反应更加敏感，经济波动对系统性风险造成的影响越显著，所以经济波动影响发挥“增效器”的作用，当银行业内部脆弱性风险改善时，经济波动对系统性风险起稳定的作用；当银行业内部脆弱性风险恶化时，经济波动会加快系统性风险的恶化速度。

我国银行业体系大致可分为大型国有银行和中小型银行两类，在银行业系统性风险的三个来源中，两类银行对不同风险来源的贡献存在显著差异。大型国有银行资金实力雄厚且有政府背景的支持，其经营的稳健性和风险抵御能力较强，而中小型银行资产规模较小，可供投资的项目范围有限，盈利状况波动较大，受经济波动的影响更多，因此银行业系统性风险中的内部脆弱性风险和经济波动影响主要来源于中小型银行。同时，大型国有银行与其他银行的资金业务往来较为频繁，在银行业网络中处于核心地位，属于系统重要性银行，这些银行一旦发生重大风险则会通过网络传染扩散至整个银行业，带来银行业系统性风险的恶化，因此银行业系统性风险中的网络关联风险主要来源于大型国有银行。

(二)模型构建

本文的模型构建分为两个部分，第一部分是采用SCCA方法度量银行业系统性风险，具体步骤如下，在使用CCA方法计算单个银行的预期损失的基础上，运用POT(Peaks Over Threshold)模型估计单个银行预期损失的边际概率分布；然后引入Copula函数刻画银行间的风险相依结构，反映银行间的网络关联情况，并估计单个银行预期损失的联合概率分布；最后采用Monte Carlo模拟估计出现系统性违约(即银行业总预期损失≥银行业总权益)的概率，为了后续数据处理的方便，将违约概率转换为违约距离来度量银行业系统性风险。

第二部分是将SCCA方法计算的银行业系统性风险分解为内部脆弱性风险、网络关联影响和外部经济波动影响。由于SCCA方法计算的联合违约距离包含银行内部脆弱性、银行间网络关联和外部经济波动三种风险来源，而CCA方法计算的违约距离仅包含银行内部脆弱性和外部经济波动两种风险来源，运用马尔科夫区制转移模型划分经济状态后，首先对CCA方法计算的违约距离进行分解，得到其不受经济状态影响即内部脆弱性风险的部分，然后对SCCA方法计算的联合违约距离进行分解，得到其不受经济状态影响即内部脆弱性风险和网络关联影响的部分，二者相减即可得到网络关联影响的部分，从而完成对银行业系统性风险的分解。

1．银行业系统性风险度量

(1)CCA方法计算预期损失。根据CCA方法构建单个银行的或有权益资产负债表，资产市值等于权益市值与风险债务市值之和，假设银行资产价值服从几何布朗运动，将需要偿还的债务作为违约点，当资产市值低于违约点时，银行出现违约。权益市值等于以资产为标的、债务账面价值为执行价格的欧式看涨期权价值，根据Black-Scholes期权定价公式有

E=AN(d1)-DBe-rTN(d2)

(1)

根据伊藤引理，银行权益市值波动率δE与资产市值波动率δA满足

EδE=AδAN(d1)

(2)

式(1)和式(2)中只有A和δA两个未知变量，其余均为已知参数，联立式(1)和式(2)建立非线性方程组，求解隐含的银行资产市值A和资产市值波动率δA。

违约距离DD是衡量银行违约风险的重要指标，违约距离上升表示违约风险改善

(3)

银行隐含的预期损失EL，即风险负债中预期无法偿还的部分，可看成以资产为标的、债务账面价值为执行价格的欧式看跌期权，所以有

EL=DBe-rtN(-d2)-AN(-d1)

(4)

违约距离和预期损失指标集中了资产负债信息和市场信息，其中债务规模DB反映了银行内部脆弱性风险特征，资产市值A、资产市值波动率δA、权益市值E和权益市值波动率δE反映了经济波动对银行风险的影响，违约距离和预期损失的变化同时受银行内部脆弱性和外部经济波动双重影响，是将内外部两种风险来源内生化的风险指标[32]。

(2)预期损失的极值分布。银行的预期损失具有厚尾特征，尾部风险暴露明显，为更好地考虑银行极端风险损失情形，使用极值理论对预期损失的极值分布进行建模。由于中国商业银行上市时间较短，极值样本数量不足，使用Block Maxima模型估计参数存在局限性。因此本文采用POT模型，对超过特定阈值的样本建模得出序列的尾部分布[34-35]。

假设EL1,EL2,…,ELn为n个独立同分布的随机变量，分别代表n家银行的预期损失，设定阈值为u，Γi=ELi-u表示银行i预期损失超过阈值的部分，超阈值样本分布可用以下条件概率分布函数进行估计

Fu(γ)=Prob{Γ≤γ|EL>u}

=Prob{EL-u≤γ|EL>u}

(5)

将式(5)进行变换可得到预期损失的概率分布函数

F(el)=Prob{EL≤el}=Prob{EL≤u}+(1-Prob{EL≤u})Fu(γ)

(6)

当阈值u足够大时，超过阈值的部分Γ服从广义Pareto分布[36]

(7)

其中，ξ为形状参数(shape parameter)，σ为尺度参数(scale parameter)，采用极大似然法对参数进行估计。

(3)预期损失的风险相依结构。在已知各银行预期损失边际概率分布的情况下，还需要考虑银行间的风险关联，即对预期损失的联合概率分布建模，从而度量银行业系统性风险。引入Copula函数刻画银行间的风险相依结构，假设n家银行预期损失边际分布F1(el1),F2(el2),…,Fn(eln)的联合分布函数为H，则存在Copula函数C满足[37]

H(el1,el2,…,eln)=C(F1(el1),F2(el2),…,Fn(eln))=Prob{F1(EL1)≤el1,F2(EL2)≤el2,…,Fn(ELn)≤eln}

(8)

基于Archimedean族函数中常为使用的Gumbel Copula和Clayton Copula对预期损失数据进行拟合，选择似然值较大的Copula构建预期损失的联合分布，其函数形式为

(9)

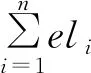
(10)

由于Copula函数解析形式复杂，实际计算中采用Monte Carlo模拟得到PDJ，步骤如下。

第一，生成n维随机数(F1(el1),F2(el2),…,Fn(eln))，其中Fi(eli)∈[0,1]；

第二，将n维随机数代入式(9)估计出的Copula函数中，计算联合分布概率值C(F1(el1),F2(el2),…,Fn(eln))；

第三，根据估计出的广义Pareto分布，结合式(6)和式(7)求出Fi(eli)(i=1,…,n)的反函数eli，并将所有机构的预期损失加总；

第五，重复计算10 000次，取所有满足步骤④的违约概率的最小值即为PDJ。

为方便进行后续数据处理和分析，将联合违约概率PDJ转化为联合违约距离DDJ。

DDJ=-N-1(PDJ)

(11)

由上述分析可以看出，与违约距离DD相比，联合违约距离DDJ通过估计银行间的风险相依结构，新增了对银行间网络关联信息的捕捉，是将银行内部脆弱性风险、银行间网络关联和外部经济波动影响三种风险来源内生化的风险指标。

2.银行业系统性风险分解

假设联合违约距离DDJ中银行内部脆弱性、银行间网络关联和外部经济波动三种风险来源相互独立，其中银行内部脆弱性风险反映的是微观的机构层面风险，是指银行自身经营性风险，与银行个体业务模式和管理方式相关；银行间网络关联风险反映的是中观的行业层面风险，是指银行同业间资金借贷、业务往来、相互持股等关联途径隐含的风险；外部经济波动风险反映的是宏观基本面的风险。

经济波动在时间序列上具有状态转移的特征，一般分为“经济收缩”和“经济扩张”两种状态，利用马尔科夫区制转移模型划分经济状态[38]，建立p阶两状态的一般化模型，即MS(2)-AR(p)模型。

(12)

εt|It-1∽iidN(0,σ(St)2)，t=1,…,T

(13)

其中，yt表示经济波动的观测变量，{St}表示不可观测的状态离散变量，服从两状态一阶平稳的马尔科夫过程，St=1,2分别表示经济处于“经济收缩”状态和“经济扩张”状态，μ(St)、Ai(St)、εt分别表示经济处于状态St时模型的截距项、自回归系数和残差项，σ(St)表示εt的标准差，It-1表示(t-1)时点的信息集。

假设t时点经济状态只与(t-1)期状态有关，与(t-1)期之前的状态无关，pij表示时点下状态i转移到状态j的概率(i=1,2;j=1,2)，构成2×2状态转移概率矩阵P

pij=P[St=j|St-1=i]

(14)

(15)

(16)

(17)

(18)

Pi1(St=1)+Pi2(St=2)=1

(19)

将系统性风险看作是银行内部脆弱性、银行间网络关联和外部经济波动的简单加总，则ts+n期外部经济波动对系统性风险的影响wJ为

(20)

|wJ|越大，经济状态在ts+n期对银行业系统性风险的影响越大。wJ>0说明外部经济波动对系统性风险的影响为正，经济状态有利于降低系统性风险；wJ<0说明外部经济波动对系统性风险的影响为负，经济状态会加剧系统性风险。

(21)

四、实证结果与分析

(一)样本选取和数据来源

考虑到数据的可获得性，由于使用CCA模型和SCCA模型时需要权益市值数据，为覆盖尽可能长的时间区间，选取中国2007年10月前上市的14家银行作为研究样本，包括平安银行、宁波银行、浦发银行、华夏银行、民生银行、招商银行、南京银行、兴业银行、北京银行、交通银行、工商银行、建设银行、中国银行和中信银行。数据时间区间为2007年10月至2021年12月。计算所需数据包括负债数据和权益市值数据，其中银行负债数据来自国泰安数据库，违约点等于短期负债与长期负债一半之和[39]；银行权益市值数据来自Wind数据库，权益市值为收盘价与股本之积，在此基础上计算权益市值收益率的波动率[40]；由于上海银行间同业拆放利率(Shanghai Interbank Offered Rate，简称Shibor)更新频率较高，无风险利率采用1年期的Shibor。

在采用CCA方法时，将14家银行作为整体进行分析，把所有银行的权益市值、违约点、资产市值加总得到银行业的权益市值、违约点、资产市值，构造中国银行业的或有权益资产负债表，计算银行业的违约距离作为中国银行业系统性风险的度量指标。在采用SCCA方法时，计算权益市值波动率的日频数据时滚动窗口为1个月，违约点计算中使用三次样条插值法将季度数据转换为日度数据[34]，最终计算出联合违约距离的日频数据。

在经济状态变量选取上，由于实际GDP增速只有季度数据，样本数量偏少，故本文采用工业增加值同比增长率作为经济状态变量[41]，数据来源于国家统计局，使用Ox3.4的MSVAR程序包对经济状态进行区制划分。

(二)银行业系统性风险度量

在CCA方法计算出各银行预期损失的基础上，选取时间窗口为1年的预期损失序列滚动计算，使用广义Pareto分布对序列的极值部分进行拟合，具体采取逐步估计检验的方式估计阈值和参数：设定阈值初始值为样本序列的最小值，通过最大似然法估计形状参数和尺度参数，随后对参数估计结果进行Kolmogorov-Smirnov 检验，若在5%的显著性水平上通过检验，则计算完毕，否则即剔除样本最小值，以剩下的样本序列最小值作为阈值再次进行估计，直至通过检验。考虑银行间的风险相依结构，借助Copula函数确定整个银行业的预期损失的联合分布，采用Monte Carlo模拟计算出联合违约距离，用以度量银行业系统性风险。

图1 中国银行业系统性风险的演变

CCA方法下计算的违约距离和SCCA方法下计算的联合违约距离在2008年9月至2021年12月期间的变化趋势如图1所示。违约距离在2008年至2012年呈现波动性上升趋势，银行逐渐摆脱金融危机困境，系统性风险改善，2013年初违约距离出现短暂性下降，2014年出现回升，在2015年受“股灾”影响达到低点，系统性风险显著恶化，2016年风险改善，违约距离处于较高水平。总体来看，违约距离在样本期间内波动较为频繁，对经济形势变化的敏感性较高。而联合违约距离计算中考虑了银行间风险关联，数值总体低于违约距离，变化趋势更加平稳，这是因为银行间网络具有风险溢出和风险承担的特性，其中风险溢出会放大系统性风险，使得联合违约距离数值较小，当出现较大冲击时系统性风险出现恶化；风险承担会使得网络能够应对较小的风险冲击而调整，系统性风险在短期内保持稳定，系统性风险变化较为平缓。

(三)银行业系统性风险分解

为更直观地研究影响系统性风险变化的因素，借助马尔科夫区制转移模型对系统性风险进行分解。假设中国经济增长过程中存在“经济收缩”和“经济扩张”两种区制，依据截距项、均值、方差等参数是否状态依赖，可将MS-VAR模型划分为多种类型[42]，本文考虑均值和方差都状态依赖的MSMAH模型，然后比较滞后一至三阶的AIC、SC、HQ指标，发现滞后一阶的AIC、SC、HQ均最小，最终选择MSMAH(2)-AR(1)模型，区制划分结果如图2所示。

图2 中国经济周期划分结果

样本期间内中国经济共发生了四次区制转移，2008年10月至2009年6月，经济处于“经济收缩”区制，2009年7月至2015年2月，经济处于“经济扩张”区制，2015年3月至2020年12月，经济处于“经济收缩”区制，2021年1月至2021年9月，经济处于“经济扩张”区制，2021年10月至11月，经济重新回到“经济收缩”区制。整体来看，区制划分结果与中国经济波动状况基本吻合，2009年受全球金融危机影响进入经济收缩期，之后经济回暖，进入经济扩张期，2015年初以来，随着我国进入“新常态”，经济增速有所下降并不断稳定，进入经济收缩期，2019年底爆发的新冠疫情导致2020年经济增速为负，而2021年随着疫情形势的缓解，经济出现强势反弹，进入短暂的扩张期，2021年10月经济增速恢复到疫情爆发之前的水平，仍然处于经济收缩期。

将整个样本区间划分为多个子区间，利用子区间的历史信息预测下一时点的不受经济波动影响的系统性风险部分，分别对违约距离和联合违约距离进行分解。选取每个子区间的长度为24个月，对2008年10月至2010年9月子区间内的工业生产指数增长率序列使用MSMAH(2)-AR(1)模型进行局部的区制划分，根据区制划分结果对子区间内的系统性风险值按所处的经济状态进行分类，估计不同状态下系统性风险值的概率分布并对其求期望，最后使用区制转移概率对期望值加权，估计2010年10月的不受经济波动影响的系统性风险部分E(DD)、E(DDJ)，之后选取2008年11月至2010年10月作为第二个子区间，估计2010年11月的E(DD)、E(DDJ)，以此类推。

2011年下半年以来银行间网络关联显著恶化了银行业系统性风险，2011-2012年网络关联对系统性风险的恶化程度不断加剧，2013-2015年影响逐渐缩小，2016-2017年负面影响继续扩大，2018年以来网络关联影响处于较为稳定的状态。网络关联对系统性风险的影响演变趋势的两极分化现象严重，在某些时间段较为稳定，其余时间段变化速率较大，这体现出银行间网络风险承担和风险溢出的功能，大部分的单个银行风险事件发生时，对其他银行的风险溢出效应有限，银行系统面临较小的风险冲击，此时风险通过网络实现缓释，并不会造成系统性风险的大幅波动；但当系统重要性银行或者较多数量银行出现风险事件时，对其他银行的风险溢出效应较大，银行系统面临较大的风险冲击，此时风险通过网络实现扩散和放大，导致系统性风险迅速恶化，反映出银行间网络“既稳健又脆弱”的特性。

图3 中国银行业系统性风险的分解

同时注意到，银行内部脆弱性与银行间网络关联影响的变动趋势存在此消彼长的关系，银行内部脆弱性风险越大，银行间网络关联对系统性风险的恶化程度越小。其原因在于二者作为银行业内的风险渠道，反映了系统性风险在银行业内的风险分配状况，当出现风险时银行既可以选择将风险留存于银行内部进行应对，也可以选择利用银行间网络将风险转移至其他银行，当银行通过机构间网络关联渠道实现风险溢出时，银行自身风险承担减少，银行内部脆弱性风险降低，同时风险传染使得银行间风险关联增强，对系统性风险恶化程度增加，使得银行业系统性风险水平并没有下降。

2011年下半年以来经济波动对系统性风险的影响以改善为主，经济波动对银行业系统性风险的影响方向与经济所在区制并不完全一致，这是因为我国近十年来一直保持较高的经济增长速度，“经济收缩”区制下经济发展势头仍然表现良好，此时经济波动并没有显著恶化系统性风险状况。同时可以发现，经济波动对系统性风险影响的变化趋势与内部脆弱性风险水平有关，经济波动影响发挥着“增效器”的作用，当银行业内部脆弱性风险改善时，经济波动对系统性风险的影响为正向，对系统性风险主要起稳定的作用；当银行业内部脆弱性风险恶化时，经济波动对系统性风险的影响为负向，加快系统性风险的恶化速度。

(四)系统性风险的差异化监管

我国银行业体系主要分为大型国有银行和中小型银行两种类型，二者在资产规模、业务模式、组织结构等方面存在显著差异，由此导致两类银行风险演变特征存在差异。而银行业系统性风险是两类银行风险的组合，为了分析银行业系统性风险中的个体来源，本文进一步将总体银行样本分为两类，计算两类银行风险的不同组成部分。在本文选取的14家上市银行研究样本中，包括交通银行、工商银行、建设银行、中国银行4家大型国有银行，其余10家为中小型银行，结果如图4-6所示。

从内部脆弱性风险来看，如图4所示，大型国有银行和中小型银行的内部脆弱性风险变化趋势与银行业内部脆弱性风险变化趋势较为一致，2015年以前，大型国有银行内部脆弱性风险远低于中小型银行，2016-2018年两类银行的内部脆弱性风险较为接近，2019年以来大型国有银行内部脆弱性风险逐渐改善，而中小型银行内部脆弱性风险变化较小，二者差距越来越明显。总体上大型国有银行内部脆弱性风险低于中小型银行，而银行业总体的内部脆弱性风险处于二者之间，因此银行业的内部脆弱性风险部分主要来源于中小型银行。

图4 不同类型银行的内部脆弱性风险比较

从网络关联对风险的影响来看，如图5所示，总体上大型国有银行和中小型银行风险受网络关联的影响均为负，且网络关联对大型国有银行风险的恶化程度更高，而网络关联对银行业总体风险的影响程度处于二者之间，反映出大型国有银行由于在银行业网络中处于核心地位，与其他银行间的网络关联较为密切，网络成为风险扩散的重要渠道，进一步带动银行业系统性风险受网络关联的影响增加，而中小型银行间的网络较为稀疏，网络对其风险影响较为有限，有利于缓释网络对系统性风险的恶化程度，因此银行业的网络关联风险部分主要来源于大型国有银行。

从经济波动对风险的影响来看，如图6所示，在除2015-2016年之外的时段内，经济波动对大型国有银行风险的影响较小且保持稳定，而中小型银行风险受经济波动的影响较大且变化较为频繁，反映出宏观经济形势的变化对于中小型银行风险具有重要作用。总体上大型国有银行风险受经济波动的影响低于中小型银行，除了2011年上半年以外，其余时段内经济波动对银行业系统性风险的影响变动趋势与中小型银行较为一致，因此银行业系统性风险中经济波动影响部分主要来源于中小型银行。

因此在对银行业系统性风险进行监管时，需要根据监管的具体风险来源，针对不同类型的银行采取差异化监管要求。为完善银行业系统性风险中的内部脆弱性风险管理，监管部门需要关注中小型银行的特质性风险，对中小银行的资产负债结构、业务模式等内部管理方面加强合规性监管，制定更为严格的监管要求；为完善银行业系统性风险中的网络关联风险管理，监管部门需要关注大型国有银行之间的资金关联度，警惕“大而不能倒”和“联系太紧密而不能倒”下的道德风险问题；为完善银行业系统性风险中的经济波动风险管理，监管部门需要关注中小型银行的经营行为，降低中小型银行业务对宏观经济形势的依赖，当经济出现较大波动时加强对中小型银行的监管要求。

图5 网络关联对不同类型银行风险的影响比较 图6 经济波动对不同类型银行风险的影响比较

五、结论

本文从中国银行业系统性风险来源入手，将SCCA模型与马尔科夫区制转移模型相结合，通过对不同经济状态的识别，对系统性风险中银行内部脆弱性、银行间网络关联和外部经济波动部分进行分解，重点研究银行间网络关联和外部经济波动对银行业系统性风险的影响，并基于不同风险来源研究银行个体对银行业系统性风险的影响。研究结论如下：第一，网络关联对系统性风险的影响演变趋势的两极分化现象严重，在某些时间段较为稳定，其余时间段变化速率较快，这体现出银行间网络风险承担和风险溢出的功能，反映出银行间网络“既稳健又脆弱”的特性。第二，银行间网络关联风险与银行内部脆弱性风险的变化趋势存在此消彼长的关系，银行通过网络关联渠道实现风险转移，银行内部脆弱性风险下降，同时银行间网络关联增强，关联风险上升。第三，经济波动对系统性风险影响的变化趋势与内部脆弱性风险水平有关，经济波动发挥“增效器”的作用，当银行内部脆弱性风险改善时，经济波动对系统性风险起稳定的作用，当银行内部脆弱性风险恶化时，经济波动会加快系统性风险的恶化速度。第四，银行业系统性风险是大型国有银行风险和中小型银行风险的组合，银行业内部脆弱性风险和经济波动影响主要来源于中小型银行，网络关联风险主要来源于大型国有银行。

从中国银行业系统性风险监管角度出发，本文提出如下政策建议：第一，监管当局应该从银行内部脆弱性、银行间网络关联影响、经济波动影响三个方面评估银行业系统性风险的变化原因，其中针对银行内部脆弱性的监管涉及资本充足率、流动性要求、杠杆要求等微观审慎监管工具，针对银行间网络关联影响的监管涉及系统重要性银行附加监管规定、跨行金融产品管理、金融基础设施管理等结构维度的宏观审慎监管工具；针对经济波动影响的监管涉及资本流动管理、市场交易行为管理等时间维度的宏观审慎监管工具。第二，本文结论显示网络关联风险与内部脆弱性风险存在此消彼长的关系，所以在管理网络关联风险时不仅需要评估政策对网络关联风险的实施效果，还需要关注政策对内部脆弱性风险的实施效果，注重结构维度宏观审慎监管工具与微观审慎监管工具的配合，减少监管套利的空间。第三，本文结论显示经济波动影响对内部脆弱性风险发挥“增效器”的作用，所以为降低经济波动对系统性风险的影响，监管重点是增强银行自身经营的稳健性，以微观审慎监管工具为主，以时间维度宏观审慎监管工具为辅，实现两种政策工具的互补和配合。第四，本文结论显示银行业内部脆弱性风险和经济波动影响主要来源于中小型银行，网络关联风险主要来源于大型国有银行，所以为提升上述政策工具的实施效果，监管当局需要根据具体风险来源，对不同类型银行采取差异化监管要求，其中微观审慎监管工具和时间维度宏观审慎监管工具的重点监管对象是中小型银行，而结构维度宏观审慎监管工具的重点监管对象是大型国有银行。