18CrNiMo7-6合金钢J-C损伤模型失效参数研究
吴少洋, 张建伟, 卢凤强, 李元鑫, 秦瑾鸿
(1.郑州大学 机械与动力工程学院,河南 郑州 450001;2.郑州大学 力学与安全工程学院,河南 郑州 450001)
材料力学行为的合理描述对准确模拟结构在不同加载工况下的响应尤为重要,而材料的损伤是材料行为描述的一个重要方面[1]。金属材料的损伤一直备受关注,诸多学者和研究人员对损伤准则进行了相关研究。
目前常用的损伤准则包括Johnson-Cook(J-C)损伤模型、Cockroft-Latham(C-L)断裂准则以及Hillerborg等基于断裂能提出的损伤准则等[2]。由于J-C损伤模型[3]考虑了应力三轴度、应变率与温度的影响,模型参数含义清晰且易于通过实验进行获取,因此被广泛应用于众多涉及材料失效破坏的有限元模拟研究中。李成等[4]采用J-C本构及损伤模型对子弹侵彻防弹钢板进行了数值模拟,再现了侵彻的动态过程,并分析了分层及间隙作用对钢板的抗侵彻能力的影响。Vasu等[5]采用J-C损伤模型对Al7075-T6材料进行了正交切削仿真研究,所预测切屑厚度与实验结果吻合良好。对材料的J-C损伤模型参数进行细致的实验测定是获得良好预测结果的重要前提。门建兵等[6]通过相关实验获得了EFP材料J-C损伤模型参数并进行了参数验证。Hu等[7]通过实验获得45CrNiMoVA 材料的J-C损伤模型参数并通过SHTB对比实验验证了参数的有效性。
虽然目前国内外学者对众多不同材料的J-C 损伤模型参数的获取和验证做了诸多相关研究,但依然缺乏针对18CrNiMo7-6合金钢材料的J-C损伤模型描述以及相关参数的实验测定。18CrNiMo7-6合金钢材料由于其出色的机械和加工性能,是重型机械装备变速箱中传动齿轮等关键构件加工制造的首选钢种[8-9]。因此确定其J-C损伤模型参数对于该材料在机械成型加工等数值模拟中有着重要的意义和价值。本文针对Johnson-Cook损伤模型开展了3个系列的力学实验,根据实验结果拟合标定了Johnson-Cook损伤模型参数,并通过Taylor冲击实验与有限元模拟验证了所得参数的有效性。
1 实验相关
1.1 Johnson-Cook损伤模型
J-C损伤模型[4]是应用较为广泛的失效准则之一。模型中损伤参数定义如下式:
(1)
式中:Δεeq为积分周期等效塑性应变增量;εf为当前时间步长失效应变。当损伤参数D=1时,材料失效。失效应变的表达形式如下:
(1+D5T*)。
(2)
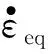
1.2 实验材料与试样制备
本研究选用18CrNiMo7-6合金钢材料,密度为7 830 kg/cm3,采用锻造加工工艺。表1为18CrNiMo7-6合金钢主要化学成分,实验所用材料均取自同一批次材料。
图1为不同缺口圆棒试样的形状和尺寸图,为了获取较大范围的应力三轴度,设计缺口尺寸R=1.5、2.5、3.5、5.5 mm,并加工有光滑圆棒试样,视R为无穷大。对每种工况进行3次重复实验。

表1 18CrNiMo7-6合金钢化学成分Table 1 Chemical composition of 18CrNiMo7-6 alloy steel %
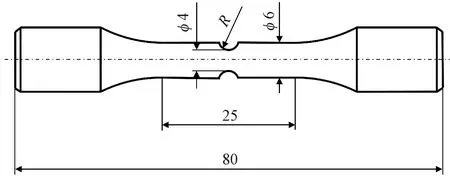
图1 缺口试样尺寸(mm)Figure 1 Size of the notched specimen (mm)
本文室温下准静态拉伸实验均在MTS 250 KN轴向疲劳试验系统上进行。高温下准静态拉伸实验所用设备由WPS-25H材料性能动静分析测试试验机与HSYS-300A型高低温环境试验箱组成。对于动态拉伸实验,本文采用ALT 1200分离式霍普金森拉杆,其实验装置简图如图2所示,其中拉杆的杆径为15 mm,数据的采集与分析由ALT1200型超动态数据采集系统完成。
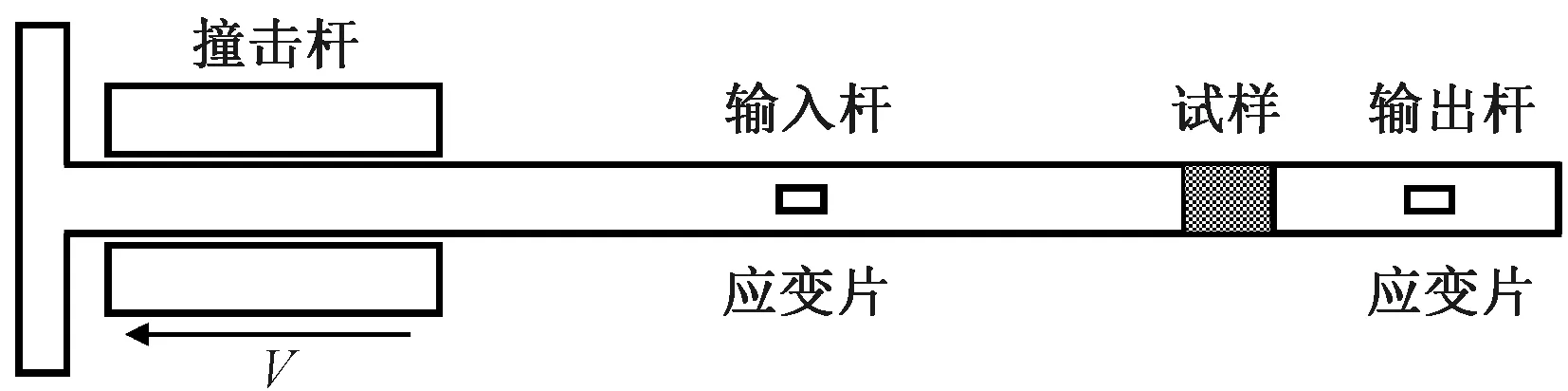
图2 霍普金森拉杆实验装置简图Figure 2 Schematic diagram of SHTB devices
2 实验结果与讨论
2.1 应力三轴度对失效应变的影响
采用缺口试样拉伸实验是获取不同应力三轴度的简单有效的方法,根据Bridgman原理[10]可采用式(3)近似计算缺口拉伸试件的应力三轴度:
(3)
式中:a为缺口试样最小横截面处的半径,mm;R为缺口底部曲率半径,mm。高玉龙等[11]研究发现在缺口试样拉伸实验初始加载时,通过式(3)计算得到的应力三轴度值较为吻合,但是随着加载过程中等效应变的不断增大,应力三轴度值发生变化。余万千等[12]在拉伸实验的基础上结合有限元模拟得到了不同时刻缺口试样的应力三轴度,并以试样断裂时刻的应力三轴度σend*或考虑应变积累效应的平均应力三轴度σsavg*进行分析,其计算方法分别如式(4)和(5)所示:
σend*=σ*|εeq-εf;
(4)
(5)
式中:εeq为等效应变。同时Goto等[13]发现,应力三轴度在缺口试样最小横截面上也是变化的。因此为了考虑这些因素带来的影响,本文通过缺口试样拉伸实验并结合有限元分析的方法进行应力三轴度以及失效应变的计算。首先进行光滑试样准静态拉伸实验,根据如图3所示的应力-应变曲线拟合得到18CrNiMo7-6材料的幂硬化本构模型[14]参数,其中材料屈服应力为338 MPa,杨氏模量为189 GPa,应变硬化指数为0.21。
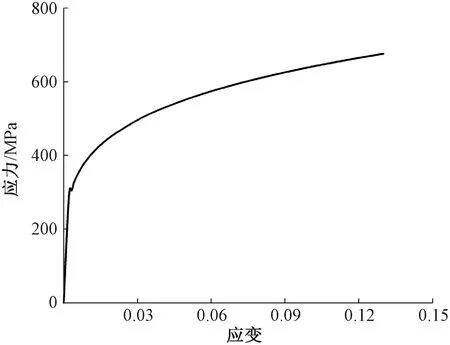
图3 18CrNiMo7-6合金钢的应力-应变曲线Figure 3 Stress-strain curve of 18CrNiMo7-6 alloy steel
随后对不同缺口试样进行准静态拉伸实验,并利用ABAQUS/Standard以相同的加载工况对不同缺口试样拉伸实验进行仿真分析。图4为缺口尺寸R=1.5 mm时仿真与实验的力-位移曲线对比,对比结果可以看出模拟与实验所得载荷位移曲线相吻合。并且从图4中可以获得试样断裂位置处所对应的位移,根据此位移在仿真中确定试样发生断裂时刻的最大等效应变,并以此应变值作为不同缺口试样拉伸下的失效应变,不同缺口尺寸试样结果如表2所示。对模拟结果进行应力三轴度的分析,图5为不同缺口试样缺口底部横截面中心点的应力三轴度随等效应变的变化曲线,其中断裂位置点即为图4所给出的失效应变位置点。从图5中发现在缺口试样初始加载段,应力三轴度值与文献[10]计算结果一致,而随着应变的增加,应力三轴度整体上呈增大趋势,并且随着缺口尺寸的增大其应力三轴度值随之减小。
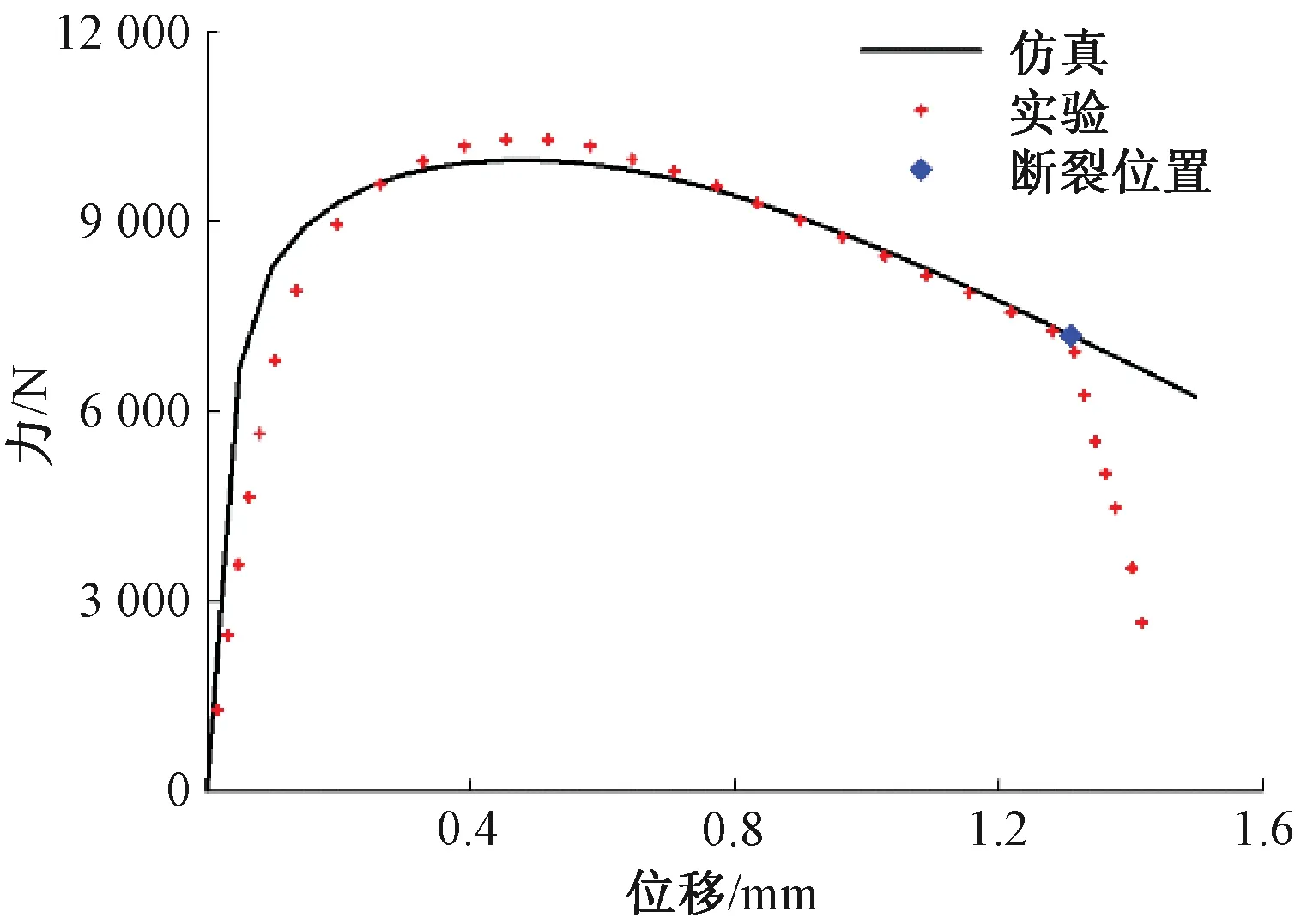
图4 仿真与实验的力-位移曲线Figure 4 Force-displacement curve of experiment and simulation
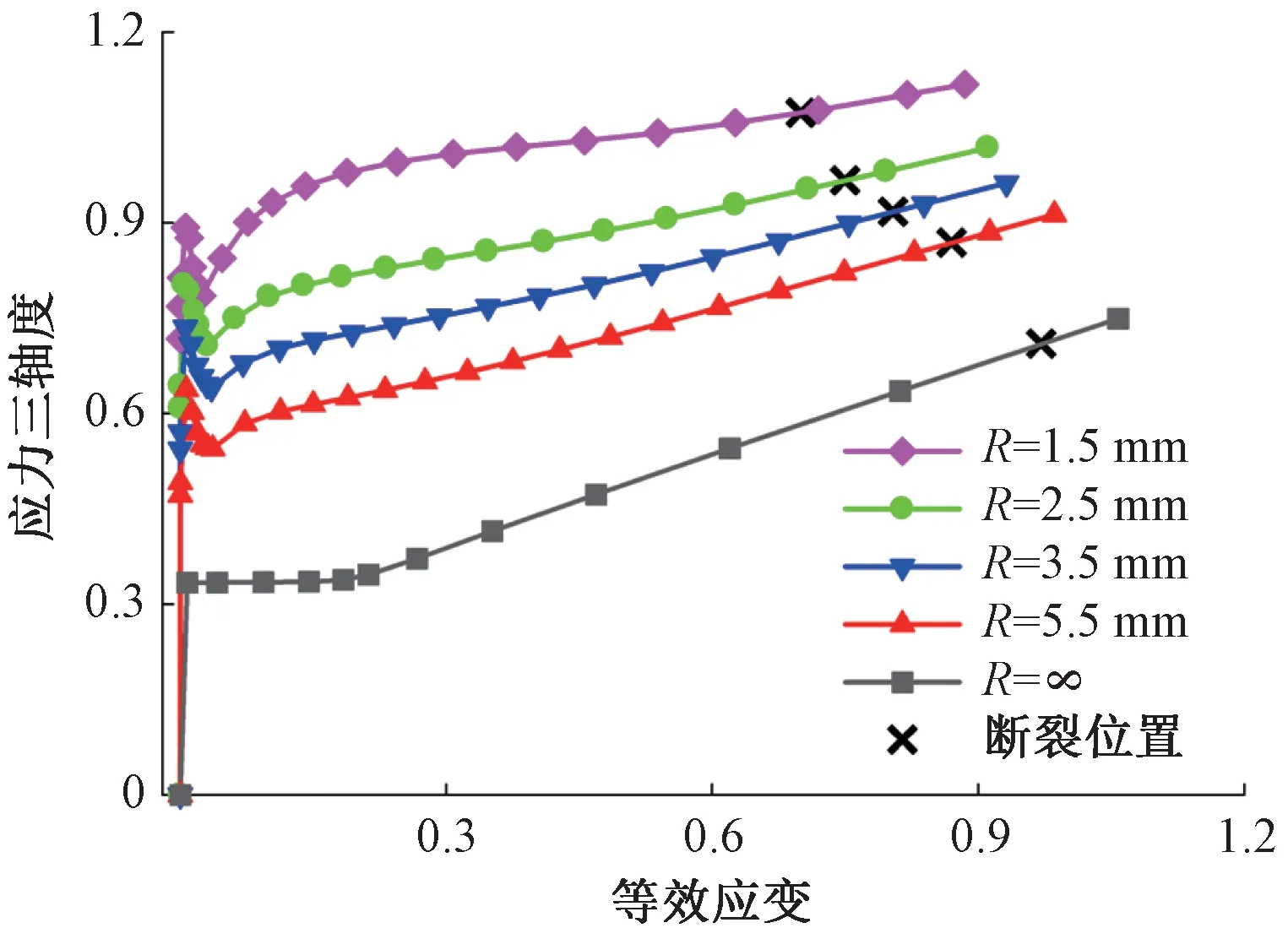
图5 应力三轴度变化规律Figure 5 Evolution of stress triaxiality
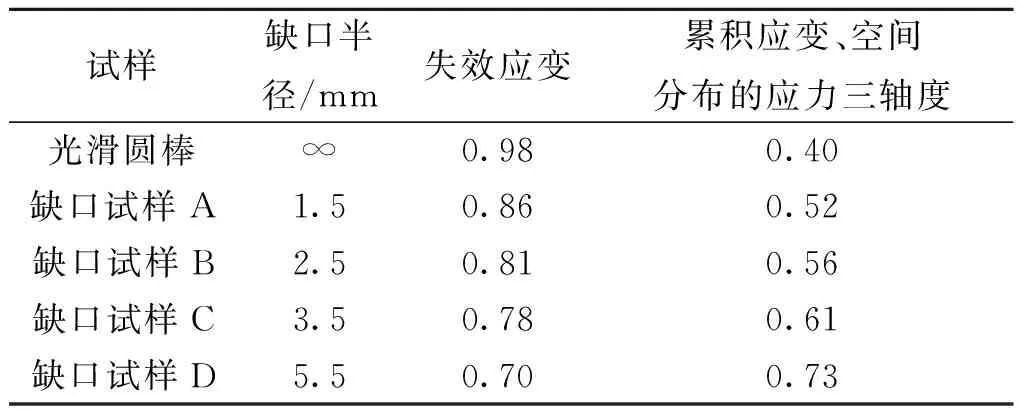
表2 失效应变与应力三轴度计算结果Table 2 Result of fracture strain and stress triaxiality
进一步分析应力三轴度在缺口试样最小横截面上的分布规律,根据式(3)~(5)计算方法以及数值模拟结果得到对应的应力三轴度沿径向的分布。图6为缺口尺寸R=1.5 mm时应力三轴度变化情况。其中r为最小横截面上距中心处的距离。从图6中可以发现不论是采用哪种方法计算得到的应力三轴度都是随着半径的变化而发生改变的,并且在横截面中心处总是最大,并随半径的增大而逐渐减小。
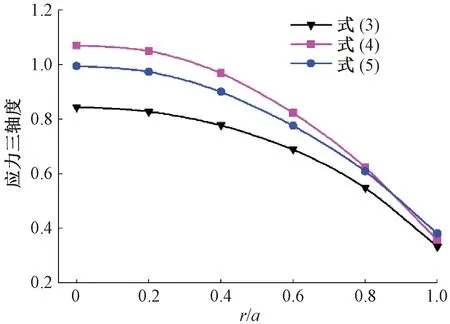
图6 应力三轴度的径向分布Figure 6 Radial distribution of stress triaxiality
通过上述分析,为了考虑应力三轴度在截面不同位置以及随应变的增加而发生变化所带来的影响,采用贾东等[15]提出的既考虑空间分布效应,又考虑应变累积效应的应力三轴度计算方法,其计算公式如下:
(6)
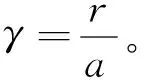
根据表2的数据对式(2)第1部分的参数进行拟合,得到失效参数D1=0.47、D2=1.31、D3=-2.36,失效应变随应力三轴度变化的拟合曲线与所得数据点对比见图7,其中拟合优度为0.99。
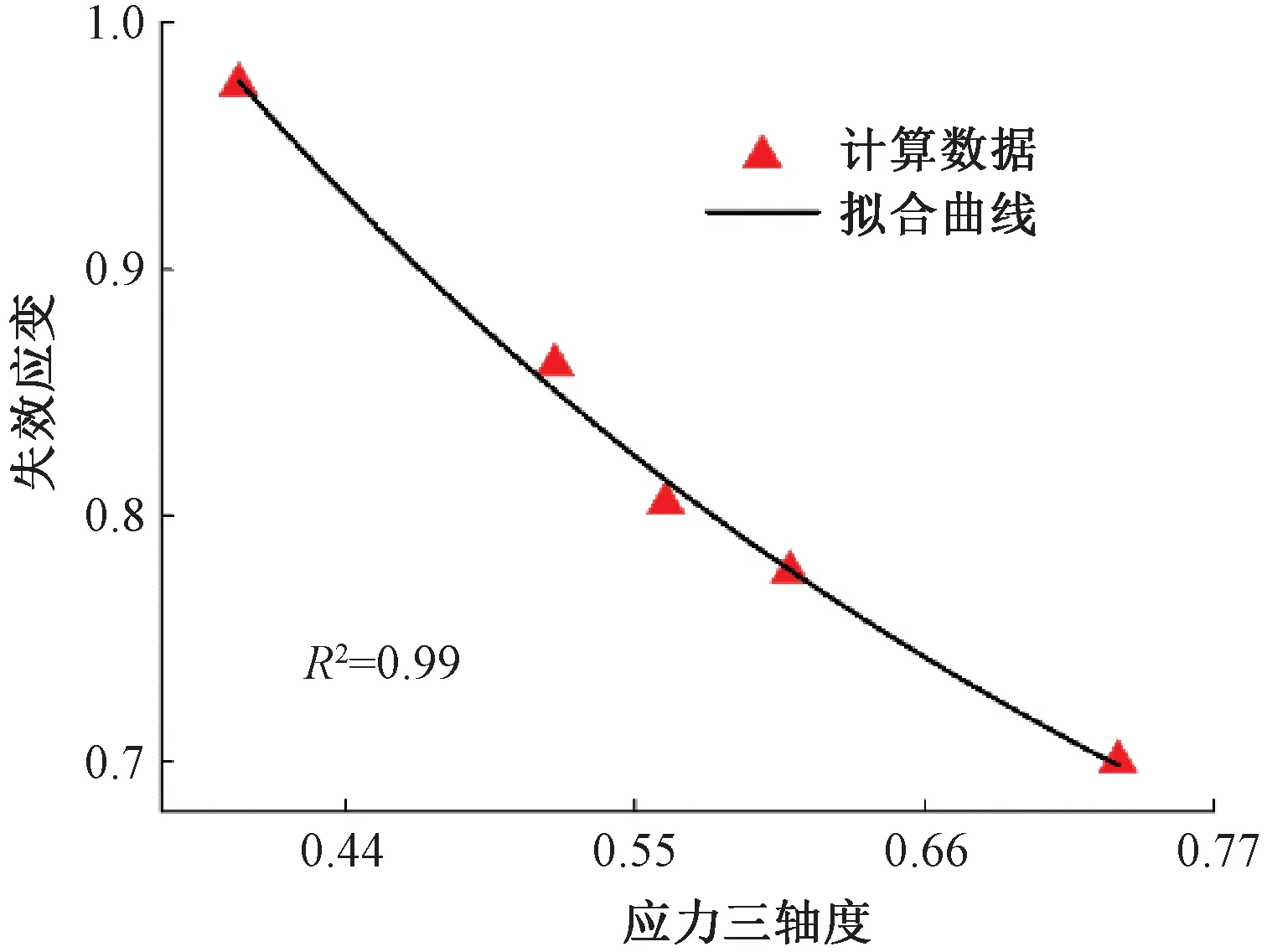
图7 失效应变与应力三轴度的关系Figure 7 Curve of failure strain and stress triaxiality
2.2 应变率对失效应变的影响
在MTS试验机上进行室温下应变率为10-3、10 s-1的拉伸实验,由拉伸速度对应变率进行控制,应变率的计算参考规范[16]所提方法。在SHTB装置上进行高应变率下的冲击实验,由贴在弹性杆上的应变片进行动态应力、应变数据的采集,通过改变打击杆的速度得到不同应力波下的应变率(1 276 s-1、2 100 s-1、2 828 s-1)。得到不同应变率下的应力-应变曲线如图8所示。从图8中可以看出随着应变率的增加,材料屈服应力也随之增大,表明材料有明显的应变率强化效应。
根据式(7)对不同应变率下被拉断试样的断口截面积进行失效应变的计算[17]。
(7)
式中:A0为试样初始横截面积;A为试样断裂时断口处横截面积。
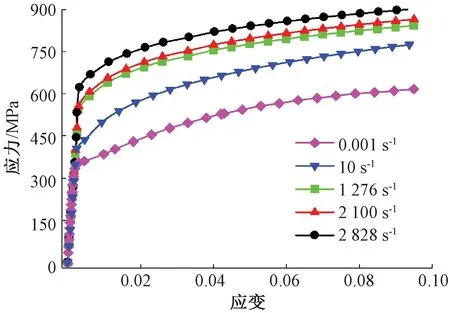
图8 不同应变率下应力-应变曲线Figure 8 Stress-strain curves at different strain rates
根据得到的数据对式(2)第2部分的参数进行拟合,实验数据及拟合曲线如图9所示,从图9中可以看出失效应变随着应变率的上升有所增加。拟合得到失效参数D4=0.012,其中拟合优度为0.90。

图9 失效应变与应变率的关系Figure 9 Relationship between failure strain and strain rate
由于在进行高应变率冲击拉伸时,试样在实验过程中产生较大温升,容易引起材料软化、韧性提高,并且SHTB实验中对于断裂应变较高的试样较难保证在一次脉冲下将试样冲断,也可能由此产生一定的误差。因此综合上述情况在拟合应变率项的参数时,拟合误差相对增大。
2.3 温度对失效应变的影响
在准静态下进行不同温度的光滑试样拉伸实验,实验中选取的温度为25、200、300、400 ℃。不同温度下的应力应变关系如图10所示。
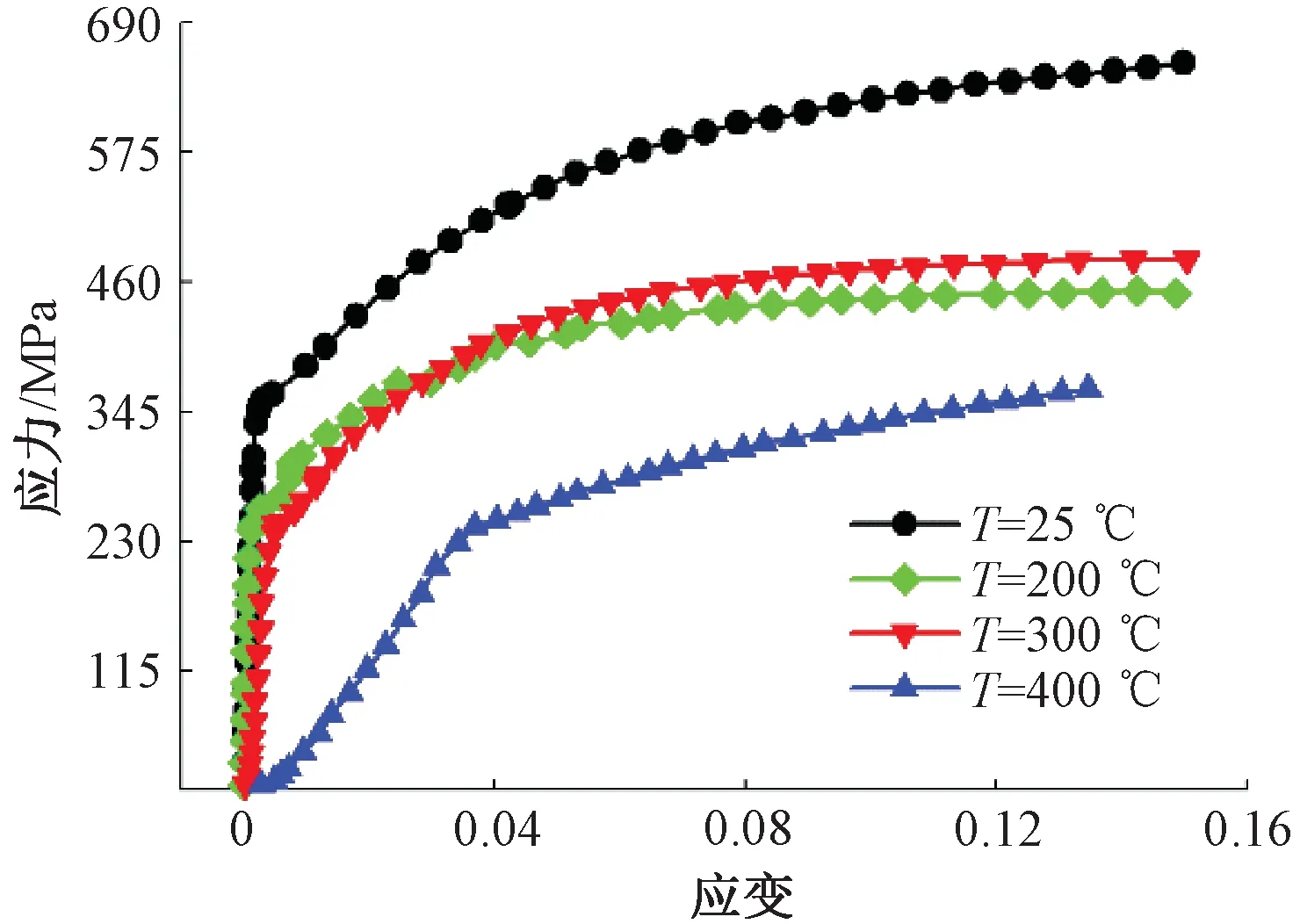
图10 不同温度下拉伸实验结果Figure 10 Tensile test results at different temperatures
从图10可以看出随着温度的升高,材料的屈服应力逐渐降低,但是在300 ℃时,材料的抗拉强度要高于200 ℃条件下的结果,并且在此温度下其断口的颜色与其他温度拉伸所得断口颜色有所不同,断口处呈现蓝色,该现象被一些学者称为蓝脆效应[18]。当材料处于蓝脆温度时其强度增加、延性降低,原因是在塑性变形过程中位错被氮和碳原子钉住以及整体位错密度的增加[19]。本实验表明18CrNiMo7-6 合金钢具有蓝脆效应,且蓝脆温度在300 ℃左右。实验结果表明随着温度的增大失效应变有所下降。拟合曲线与所得数据点对比见图11,对式(2)第3部分进行拟合,其中参考温度为25 ℃,材料融化温度为1 510 ℃,得到D5=-0.84,其中拟合优度值为0.97。至此本文得到了18CrNiMo7-6合金钢所有J-C损伤模型失效参数。
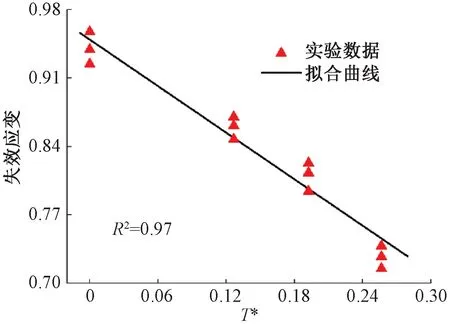
图11 失效应变与温度的关系Figure 11 Relationship between fracture strain and temperature
2.4 参数检验
为了验证实验所得的J-C损伤模型失效参数是否合理,开展了18CrNiMo7-6合金钢Taylor冲击实验。该实验主要用于检验其他方式所获得的材料动态本构关系、损伤模型及其参数[1]。本文中Taylor 冲击实验在南阳理工学院一级轻气炮上进行,装置介绍见文献[20]。实验中采用型号为FASTCAM SA-Z 高速摄像机监控发射试样的运行姿态和破坏情况。实验中弹体尺寸为φ6×30 mm,靶体尺寸为φ55×20 mm,靶体材料为高强装甲钢板,在实验后没有出现明显变形,可认为其在碰撞中保持弹性。采用有限元软件对冲击实验进行模拟,模型参数由实验所获取,并按照实验情况进行建模计算。其中杆弹为可变形体,靶板设为刚体。杆弹和靶板的网格划分均为八节点线性六面体单元(C3D8R),网格尺寸为0.2 mm×0.2 mm×0.2 mm。对靶板添加固定约束,对工件添加平行于轴线方向的初速度,大小与实验保持一致。
设置弹体速度分别为290 m/s和430 m/s。在290 m/s速度下试样底部未发生破坏;当速度增大至430 m/s时,观察到试样底部发生破坏,其破坏形式为花瓣开裂模式。图12给出了不同速度下数值模拟结果与实验结果的比较,可以看出两种结果下试样变形情况一致。实验与数值模拟得到冲击后的弹体高度h与底部直径M记录如表3所示。从表3中试样的变形数据以及相对误差可以看出,模拟结果与实验结果吻合较好,表明了对于18CrNiMo7-6合金钢材料在高速冲击等涉及材料失效行为的模拟时,所选用的J-C损伤模型是合适的,能够对该材料的失效行为进行合理的描述,并且也验证了本文针对此模型所开展的一系列实验得到的损伤参数是合理有效的。

图12 数值模拟与实验结果形态对比Figure 12 Comparison of numerical simulation and finite element results
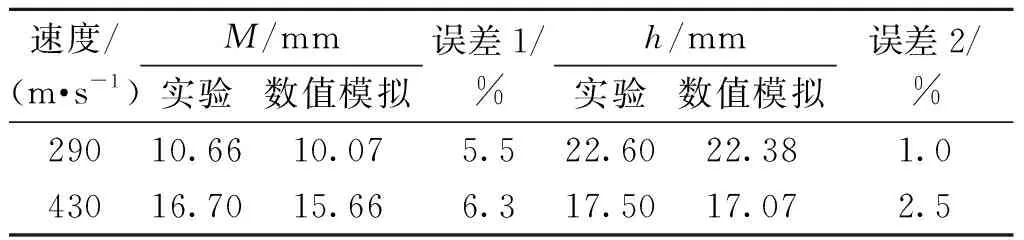
表3 数值模拟与实验结果比较Table 3 Comparison of experimental and numerical simulation results
3 结论
(1) 针对18CrNiMo7-6合金钢材料开展了缺口试样拉伸实验,结合数值模拟确定了既考虑空间分布效应,又考虑应变累积效应的应力三轴度的计算方法,得到了应力三轴度与失效应变的关系;通过不同温度下的拉伸实验发现了材料的屈服强度与失效应变随温度的升高而降低;从不同应变率下的实验结果可以看出随着应变率的升高,材料有较为明显的强化效应,其失效应变也随应变率的增大而增大。根据以上实验结果拟合得到了18CrNiMo7-6合金钢的J-C损伤模型参数,拟合优度表明拟合效果较好。
(2) 开展了18CrNiMo7-6合金钢的Taylor冲击实验,得到了弹体290 m/s和430 m/s冲击速度下的变形状态。根据拟合得到的损伤参数对Taylor冲击实验进行数值模拟。在弹体冲击速度为430 m/s时,实验与仿真得到的冲击试样均发生了破坏,对比弹体的破坏状态发现两者吻合较好,表明了本文针对18CrNiMo7-6合金钢材料进行失效行为的模拟时,所选的J-C损伤模型是合适的,亦表明了通过实验所获得的损伤参数是合理有效的。
——“长三角合金钢材料与制品产业链专刊”前言

