基于差分特征的间歇采样转发干扰辨识与抑制方法

盖季妤 姜 维 张凯翔 梁振楠 陈新亮*④ 刘泉华

①(卫星导航电子信息技术教育部重点实验室(北京理工大学) 北京 100081)

②(北京理工大学重庆创新中心 重庆 401120)

③(电子信息控制重点实验室 成都 610036)

④(北京理工大学长三角研究院(嘉兴) 嘉兴 314019)

1 引言

现代雷达面临的电磁环境日益复杂，各类电子干扰严重制约了雷达探测性能。采用数字射频存储(Digital Radio Frequency Memory,DRFM)技术的间歇采样转发式干扰机通过对雷达发射信号进行切片采样、重复转发，在雷达接收端形成多假目标干扰效果，具有使用灵活、适应性强、威胁性大的特点，已成为雷达干扰技术的主流方式之一[1-8]。

随着间歇采样转发干扰技术的发展，国内外诸多学者在空域、波形域、时频域对干扰的辨识与抑制方法开展了大量研究。在空域，文献[9]利用多通道阵列自适应波束形成技术实现干扰抑制，但当干扰机位于雷达发射波束主瓣时，在空域抑制干扰的同时也会造成目标能量的严重损失[10]。在波形域，可通过设计脉内正交波形[11,12]、多普勒敏感波形[13,14]、失配滤波器[15-17]有效抑制间歇采样转发干扰，但是此类方法需要求解复杂的波形优化问题，难以实时应用于快速变化的干扰场景。在时频域辨识并抑制间歇采样转发干扰的方法主要有两类：一是由时频图估计信源时频参数，辨识并重构干扰，然后与雷达接收信号作差以实现干扰抑制[18]；二是基于时频图构造时频域带通滤波器以抑制干扰[19-21]。其中文献[19,20]对去斜后的雷达接收信号做时频分析，提取纯目标片段构造时频域带通滤波器；文献[21]对雷达接收信号的脉压结果做时频分析，提取时频图频率维峰值3 dB宽度特征以辨识目标与干扰，并根据辨识结果设计滤波器以获得仅含目标的时频图。上述时频域干扰辨识与抑制方法均需做短时傅里叶变换进行时频分析。短时傅里叶变换在时域滑窗降低了时频域分辨率，对于第1类方法，会降低参数估计精度，影响干扰信号的重构与抑制；对于第2类方法，会导致纯目标样本的污染或丢失，影响带通滤波器的构造。另外时频分析复杂度高且需要较大的存储空间，对雷达系统有较高的硬件要求。

不同于传统空域、波形域、时频域的间歇采样转发干扰抑制方法，本文考虑在原匹配滤波的过程中添加“差分窗”以提取雷达接收信号的多阶差分特征，利用目标回波与干扰在差分域上的差异，以第1阶差分特征与其他阶差分特征总能量之比为统计量，在辨识并抑制干扰的同时实现目标的检测。所提方法不需进行复杂的寻优运算、时频分析，且有较好的干扰辨识与抑制、目标检测性能，适用于工程实践。

2 原理

2.1 信号建模

假设雷达发射信号为矩形包络线性调频信号，写为

其中，TP是发射信号脉宽，r ect(t/TP)表示宽度为TP的矩形窗，定义为

发射信号的相位

其中，f0是载频，k是线性调频信号的调频斜率。设目标到雷达的距离为R0，目标回波信号可表示为

其中，AT是目标回波幅度，τ0=2R0/c，c是光速。

间歇采样转发式干扰机对采集到的雷达发射信号进行切片采样、存储、转发，本文考虑基本的间歇采样重复转发干扰模型[21]：设干扰机采样NS次，采样结束后立即重复转发NR次，雷达接收到的干扰信号可表示为

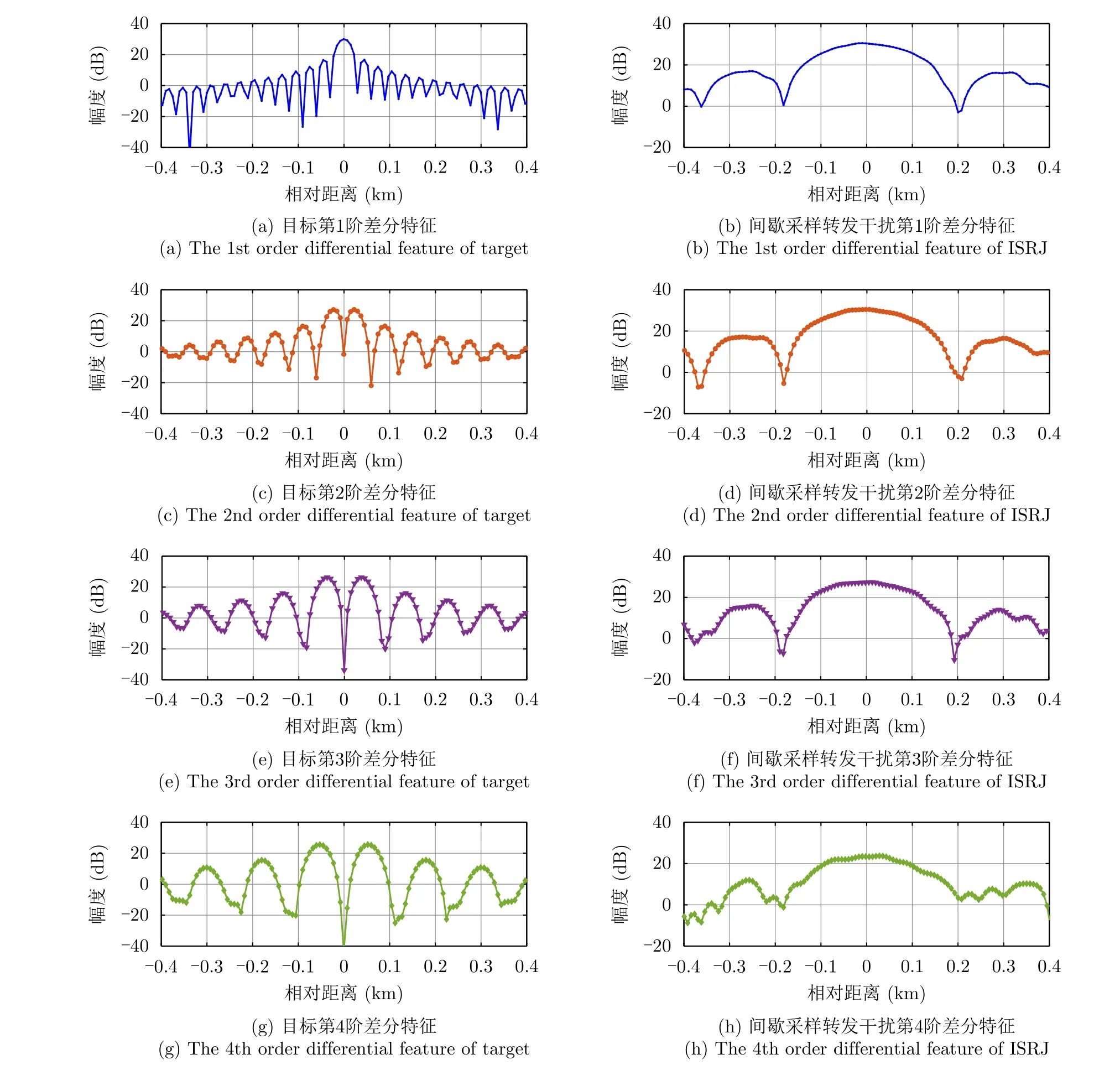
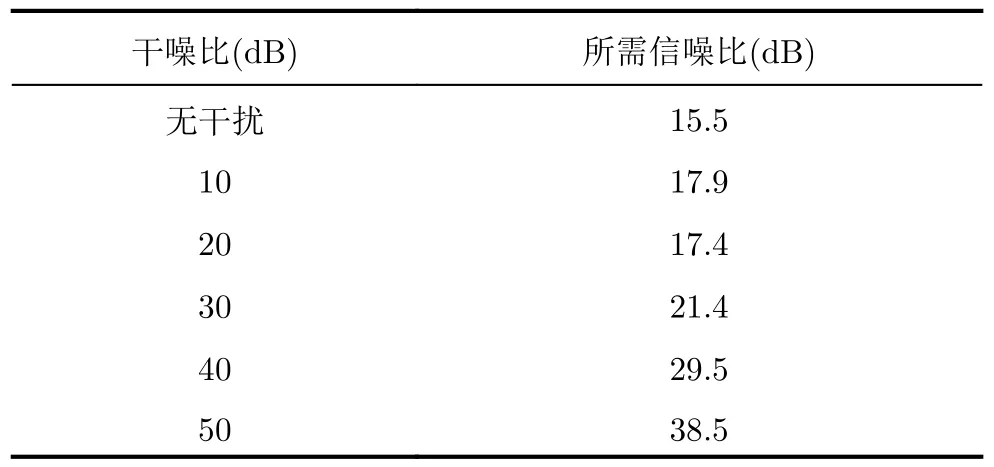
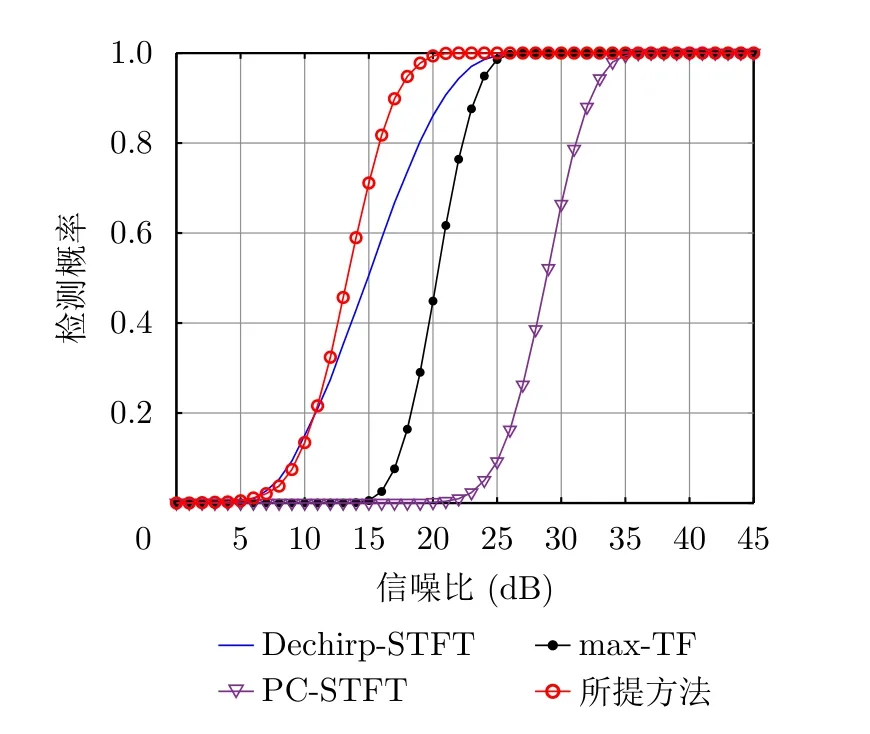
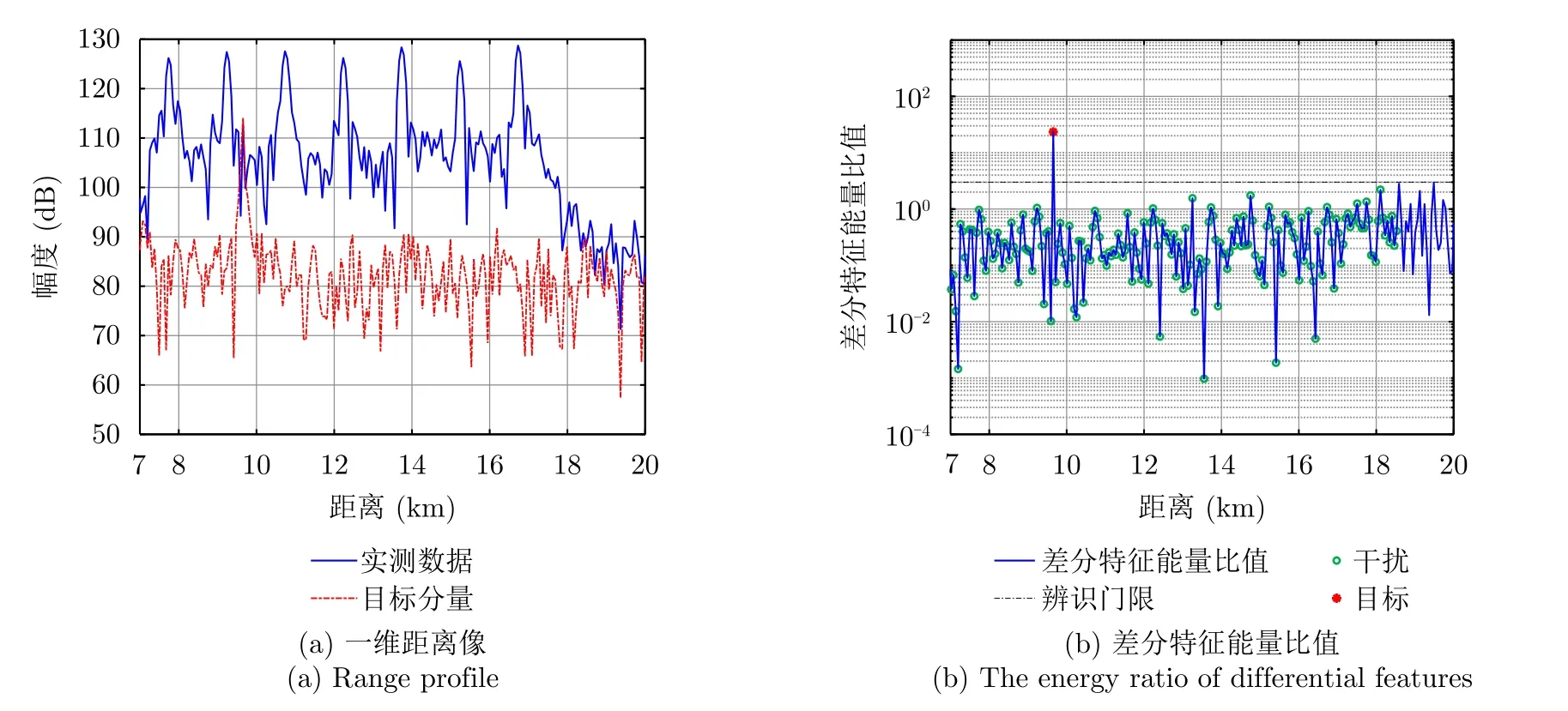
其中，AJ是 干扰幅度，τS是干扰机与雷达之间距离对应的延时，TJ是切片宽度，TJ

图1 间歇采样转发干扰示意图Fig.1 Schematic diagram of ISRJ

这样，雷达接收信号可以写为

其中，n(t)是噪声分量。

2.2 差分特征

常规雷达采用的匹配滤波处理，即脉冲压缩过程，可表示为

其中，符号∗表示卷积，h(t)=(-t)是匹配滤波器的冲激响应函数[1]。匹配滤波也可以视为对目标回波的特征提取，但它所提取的一维特征仅适用于区分目标回波和噪声，无法区分目标回波与干扰。

为有效区分目标回波与干扰，考虑利用如式(8)

所示的分段窗函数wM(t)对h(t)加权以构造一种冲激响应函数为

的滤波器。其中，分段窗函数wM(t)将 长度为TP的区间平均分成了M等份，每份的长度为TC=TP/M，每份的取值记为cM(m),m=0,1,...,M -1。为了使该滤波器对目标回波的响应为0，而对干扰信号的响应非0，该滤波器的冲激响应函数(t)应满足

为此，本文选取窗函数的各项系数cM(m),m=0,1,...,M -1为如表1所示的归一化差分序列。

表1 归一化差分序列Tab.1 Normalized differential sequence

该归一化差分序列满足

可见：在M＞1时有

所示的第M阶差分特征提取方法，(t)称 为差分参考信号，wM(t)称 为差分窗函数。特别地，当M=1时，对应的第1阶差分特征x1(t)即为常规匹配滤波结果。

这样，雷达接收信号中目标分量的第M阶差分特征可表示为

其中

在目标位置处有

同理，雷达接收信号中干扰分量的第M阶差分特征可表示为

在干扰位置处有

式(21)的取值与切片位置、切片脉宽有关，一般情况下，xJM(τS+n1TJ+n2TS)≠0。

以干扰机对发射信号的前1/6段进行采样、转发为例，目标回波和干扰的第1至4阶差分特征如图2所示。可见对于目标回波，除匹配滤波结果外，采用上述方法得到的其他阶差分特征xTM(t),M/=1都在目标位置处存在一个幅度相比于附近位置较低的凹口；对于干扰信号则不存在这种现象，目标回波和干扰信号在差分特征空间中表现出显著的差异。

图2 目标与间歇采样转发干扰差分特征对比Fig.2 Comparison of the differential features between target and ISRJ

2.3 判决准则

常规雷达将匹配滤波结果通过平方律检波器后，与门限γ比较进行目标检测，判决准则如式(22)所示：

其中，H1表 示存在目标，H0表示仅存在噪声。判决结果可表示为

检测门限γ由仅存在噪声时y1(t)的分布和常规雷达虚警概率决定。由于第1阶差分特征x1(t)不能体现目标回波与干扰信号的差异，上述判决方法仅能在无干扰的情况下检测目标，在有干扰的情况下则会出现大量虚警。

为充分利用目标回波和干扰在差分特征空间的差异，有效抑制干扰造成的虚警，提升雷达在干扰条件下的检测性能，本文提出用如下新的判决准则代替常规雷达目标检测方法：

其中，r1(t)是式(23)定义的常规雷达目标检测方法的判决结果，r2(t)是 对过常规检测门限γ的备选信源的辨识结果，辨识方法如式(25)所示：

其中，R(t)构造为第1阶差分特征的能量与其他2阶至Mmax阶差分特征的能量积累结果之比，如式(26)所示：

门限∊可根据最小错误概率准则[22]，由目标、干扰处R(t)的分布决定。由2.2节理论分析可知，若不考虑干扰，目标处的第2阶至Mmax阶差分特征的数学期望为0，仅表现为噪声，差分特征的能量积累结果接近为0，差分特征能量比值R(t)在目标处出现很高的尖峰。对于干扰信号，其恰好与差分匹配滤波器正交的概率极低，此类事件可以忽略，因此干扰处的第2阶至Mmax阶差分特征与干噪比强相关，即干扰信号越强，差分特征越大，干扰的高阶差分特征能量积累结果与第1阶匹配滤波结果的能量随干噪比同步提高。因此差分特征能量比值R(t)在干扰处的响应不高，与其在目标处的响应差异显著。值得一提的是，上述针对干扰的分析亦适用于多个干扰时域重叠的场景，该方法在多干扰场景下仍然有效。

综上所述，本文提出的间歇采样转发干扰场景下的目标检测方法流程图如图3所示。

图3 基于差分特征的间歇采样转发干扰辨识与抑制流程图Fig.3 Flow chart of the ISRJ identification and suppression based on differential features

2.4 性能指标

将雷达回波信号在匹配滤波、平方律检波后的结果y1(t)在纯噪声、目标、干扰处的概率密度函数分别记作f0(y),fT(y),fJ(y)；差分特征能量比值R(t)在纯噪声、目标、干扰处的概率密度函数分别记作g0(y),gT(y),gJ(y)。将噪声、干扰判决为目标会发生虚警，虚∫警概率可表示∫为

检测概率可表示为

3 仿真结果与性能分析

3.1 基于仿真数据的性能分析

3.1.1 参数设置

本文考虑如下仿真场景：雷达接收信号中存在一个目标、两组间歇采样转发干扰，噪声为零均值复高斯白噪声。仿真数据信源参数如表2所示。

仿真设置常规雷达检测的虚警概率为10-6，噪声功率归一化后，平方律检波器的输出服从参数为1的指数分布，对应检测门限γ为13.82。将最高差分阶数Mmax设为6，在各干噪比、信噪比下分别做104次蒙特卡罗仿真，统计R(t)的分布，结果如图4所示，可见：在干扰、目标处，R(t)的取值有明显差异，且信噪比越大，两者差异越大。

图4 不同干噪比、信噪比下，干扰、目标处差分特征能量比值的概率分布Fig.4 The probability distribution of differential features energy ratio under different jamming-to-noise ratio and signal-to-noise ratio for ISRJ and target

下面考虑用统计方法获得辨识门限∊。首先统计表2给出的所有干噪比、信噪比下干扰、目标两类样本处R(t)的分布，如图5(a)所示。然后计算两类辨识错误(干扰辨识为目标、目标辨识为干扰)概率之和与辨识门限∊的关系，如图5(b)。由最小错误概率准则设置辨识门限∊为1.79，此时干扰被判决为目标的概率小于0.67%，目标被判决为干扰的概率小于0.19%。

表2 仿真数据信源参数Tab.2 Source parameters for simulation data

图5 由最小错误概率准则确定辨识门限∊Fig.5 The determination of identification threshold ∊ by minimizing the probability of error

综上所述，设置仿真参数如表3所示。

表3 仿真参数Tab.3 Simulation parameters

3.1.2 特征提取

设置脉压后信噪比为25 dB，干噪比为30 dB；目标出现在26 km处，两干扰出现在20～30 km处。雷达接收信号各分量匹配滤波结果(即一维距离像)如图6(a)所示，目标、干扰均可过常规检测门限γ被判决为待辨识的备选信源。提取差分特征并计算辨识所用的差分特征能量比值R(t)，如图6(b)所示，可见R(t)在目标处出现很高的尖峰，在干扰处的响应相对较低，干扰得以有效辨识与抑制。

图6 仿真数据间歇采样转发干扰辨识与抑制结果Fig.6 ISRJ identification and suppression results for simulation data

3.1.3 检测性能分析

在无干扰场景下，遍历雷达接收信号的信噪比，在各信噪比下做500次蒙特卡罗仿真，所提方法与常规检测方法的检测性能曲线如图7(a)所示，可见两者近似重合，辨识门限几乎不影响目标的检测性能。在干扰场景下，遍历雷达接收信号的信噪比、干噪比，在各信噪比、干噪比下分别做500次蒙特卡罗仿真，所提方法的检测概率如图7(b)所示。在不同干噪比下，为达到95%的检测概率，所需的信噪比如表4所示。当干噪比小于25 dB时，所提方法在当前仿真场景下的检测性能几乎无损失；当干噪比大于25 dB时，所提方法的检测性能存在一定的损失但仍有可能检测到高信噪比的目标。

表4 不同干噪比下，检测概率为95%时所需的信噪比Tab.4 When the detection probability is 95%,the required signal-to-noise ratios under different jamming-to-noise ratios

图7 目标检测概率Fig.7 Target detection probability

假设目标位置已知，仅考虑干扰抑制对目标检测性能的影响，将本文所提方法与文献[19]的方法一、文献[20]、文献[21]这3种典型的时频域滤波算法进行对比仿真，将这3种方法分别简称为Dechirp-STFT (Short-Time Fourier Transform),max-TF(Time-Frequency),PC-STFT (Pulse Compression-STFT)。设置脉压后干噪比为30 dB，其他仿真参数与无干扰场景相同，短时傅里叶变换窗长为6.4 µs，滑窗步进为0.05 µs。4种方法在目标处的检测性能如图8所示。可见在当前仿真场景下，为达到95%的检测概率，本文所提方法相比于3种典型的时频域滤波算法所需的信噪比至少改善4.2 dB。

图8 4种方法检测性能对比(仿真数据)Fig.8 The detection performance comparison of the four methods (simulation data)

3.2 基于实测数据的性能分析

3.2.1 参数设置

在间歇采样转发干扰场景下，采集实测数据，具体信源参数如表5所示。

表5 实测数据信源参数Tab.5 Source parameters for measured data

为便于分析，关闭干扰机，采集纯目标回波数据，作为干扰场景下实测数据的目标分量。仿真设置最高差分阶数Mmax为3，辨识门限∊为3，其他参数与3.1节相同，此时干扰被辨识为目标的错误概率为0.28%。

3.2.2 特征提取

实测数据及其目标分量的一维距离像如图9(a)所示，目标几乎被干扰淹没。用本文所提方法提取信号差分特征并计算差分特征能量比值R(t)如图9(b)所示，可见R(t)在干扰处的响应明显低于目标，目标得以显露。

图9 实测数据间歇采样转发干扰辨识与抑制结果Fig.9 ISRJ identification and suppression results for measured data

3种典型的时频域滤波算法Dechirp-STFT[19],max-TF[20],PC-STFT[21]对去斜后的回波信号或一维距离像做时频分析，然后由目标、干扰时频分布特征的差异构造滤波器以抑制干扰。实测数据及其目标分量的时频图、去斜后信号时频图、一维距离像时频图如图10所示。由图10(b)和图10(e)可见，干扰信号在时域将目标回波完全覆盖，从时频图中无法提取纯目标片段构造滤波器，Dechirp-STFT和max-TF方法失效；由图10(c)和图10(f)，实测数据干扰能量较强且时频图精度低(采样率为2.5 MHz)，导致目标与干扰粘连而难以分辨，PC-STFT方法失效。

图10 时频图Fig.10 Time-Frequency distribution

4 结语

本文提出了一种信号差分特征提取方法，利用目标回波、间歇采样转发干扰信号在差分特征空间上的显著差异，以第1阶差分特征与其他阶差分特征总能量之比为统计量，设计判决准则以实现干扰辨识、抑制以及干扰场景下的目标检测。由于难以解析求得目标、干扰处差分特征能量之比的分布，本文亦给出了用统计方法设置辨识门限的仿真结果。本文仿真验证了雷达回波信号差分特征能量之比可在目标处出现很高的尖峰，而在干扰处其响应相对较低，利用该差异可使干扰得以有效辨识与抑制。在无干扰场景下，所提方法与常规检测方法的检测性能曲线近似重合；在干扰场景下，仿真结果表明所提方法相比于目前已有的3种典型时频域滤波算法具有更好的目标检测性能。