滑坡碎屑流运动及堵江堰塞体堆积特性模型试验

王 涓，宋 丽 婧，刘 轶，廖 海 梅

(贵州大学 土木工程学院，贵州 贵阳 550025)

0 引 言

由降雨、地震、冰雪融化、火山喷发等因素触发山体崩塌、滑坡、泥石流阻塞河道而形成的天然堆积体称为堰塞体。堰塞体的物质结构往往比较松散，颗粒间的胶结情况较差，当上游库水位迅速上涨、静水压力陡增时，堰塞体极易遭受破坏。堰塞体的形成具有突发性、高危险性，而人类活动空间范围的迅速扩展也加剧了堰塞体的致灾风险，致使上下游区域的人民生命财产安全及生态环境稳定受到严重威胁。其中滑坡碎屑流是形成堰塞体的一种主要物质来源，通常具有规模大、运动机制复杂等特点，致使其造成的堰塞体特性至今尚未被完全掌握[1-5]。例如2018年西藏白格村金沙江右岸先后2次发生滑坡堵江，造成的堰塞湖与溃坝洪水给沿岸居民与生活基础设施带来巨大灾害[6]。2008年汶川地震，发生大规模滑坡并堵塞通口河形成库容近3亿m3的唐家山堰塞湖，对下游百万群众构成巨大威胁[7]。

目前针对滑坡碎屑流形成的堰塞体研究方法主要包括现场勘察、物理模型试验及数值模拟等。邓建辉等[6]通过对白格滑坡现场勘察资料的分析，研究滑坡产生的地质环境、滑坡堆积区特性和产生诱因等条件，分析总结了白格滑坡形成机制与过程。周月等[2]通过开展物理模型试验，模拟滑坡运动过程，对滑体运动特性进行分析，得出了滑坡运动过程中冲击破碎是能量耗散的重要因素。吴建川等[8]和张龙等[9]利用PFC3D软件模拟了滑坡运动过程和堵江堆积体形态，并分析了灾害影响范围。同时，滑源体物质组成、滑坡路径地形条件对滑坡碎屑流运动过程具有重要影响。周公旦等[10]通过泥石流滑坡颗粒物质运动的离散元分析，提出了滑体颗粒分选作用能增强颗粒流动性从而影响颗粒运动的流态。王玉峰等[11]以谢家店子滑坡地形条件为基础，开展相关物理模型试验并量化分析了滑坡流态化过程及堆积特性，发现滑坡运动路径中复杂地形的分布会引起碎屑流能量的耗散从而影响碎屑流的运动距离。此外，滑坡碎屑流在运动过程中常伴随碰撞飞溅的现象，其在滑动发生的斜坡甚至对岸斜坡上都会发生，因此会出现最大坝高在对岸的情形[12-14]。例如1987年7月在意大利Adda River发生的大体积滑坡堵江事件，碎屑物在河谷对岸爬高约300 m[15]；2008年汶川地震形成的枷担湾堰塞坝，其最大坝高也出现在对岸；2008年唐家山滑坡强烈碰撞对岸山体，使堰塞体呈现出边缘破碎严重、中部较为完整的结构特征[11，16]。

天然滑坡运动速度快、运动过程短，目前技术尚难以捕捉其运动全过程，而物理模型试验在数据监测方面具有较好的可实现性，因此模型试验是分析滑坡运动和堰塞体几何形态、物质组成特征的重要研究手段。国内外学者开展了大量滑坡运动与堆积体过程的几何学、动力学模型试验研究，其中大部分基于碎屑流的运动机制，研究颗粒尺寸、滑坡体积等不同因素对滑体运动特征和沉积特性的影响。Manzella[17]、Scheidegger[18]、Davies[19]等通过无侧边约束的斜面进行干颗粒流试验，并与现实案例数据进行比较，提出了沉积物纵向标准化范围；ManzellaI[20]、Denlinger[21]等通过分析影响因素与滑体运动过程、堰塞体堆积特征之间的关系，建立了与速度相关的能量耗散模型。郝明辉等[22]通过开展室内模型试验，研究了碎屑粒径、滑床粗糙度和挑坎对滑体运动特性的影响，但未量化其影响因素对堆积体几何特性的影响。葛云峰等[23]通过PIV技术分析滑体运动过程，获得了滑体的速度和位移等运动参数，阐述了滑体颗粒间存在碰撞及能量传递现象。

通过物理模型试验研究滑体运动过程，揭示不同因素对堆积特性的影响，具有较强的可行性，但现阶段研究滑坡堰塞体形成过程的模型试验研究还较少。本文以碎屑物作为滑体，采用室内滑槽物理模型试验模拟滑坡碎屑流堵江运动过程及其堰塞体特性，研究滑坡碎屑流堰塞体的形成过程，分析滑坡体体积、滑体物质及滑床坡度对堰塞体几何形态与颗粒分布的影响，并进一步定量描述了颗粒粒径、滑槽坡度和滑体体积对堰塞体堆积特性的影响。实验过程中，采用1台高速摄像机(千眼狼高速2F04，最大帧率可达到4 700)和4台摄像机观察滑坡-堵江运动全过程。最后利用卷尺和设置装置的参考点获取堰塞体的关键几何参数，并通过透明玻璃截取堰塞体3个横断面，进而推测堰塞体内部颗粒的分布规律。

1 试验方法及试验过程

1.1 试验装置

试验装置包括模拟滑坡运动的斜槽和模拟河道的横槽两部分，如图1所示。斜槽为矩形断面，总长4.5 m，宽0.5 m，深0.5 m，与地面夹角范围为30°～60°，在距离顶端0.5 m处设置了一个闸门。为方便观察，滑槽两侧及底部均采用透明亚克力板材质，并在两侧的亚克力板底部标志了刻度，精度为1 mm。为近似模拟天然河道形状，横槽采用梯形断面，总长2 m，下底宽0.36 m，两侧斜边长0.6 m，坡角为50°。为记录完整的试验在斜槽侧面布置了4台录像机，并采用高速摄像机获得滑体在出口的运动参数。本次试验没有考虑水流对滑体入河堵江过程和堰塞体特性的影响。

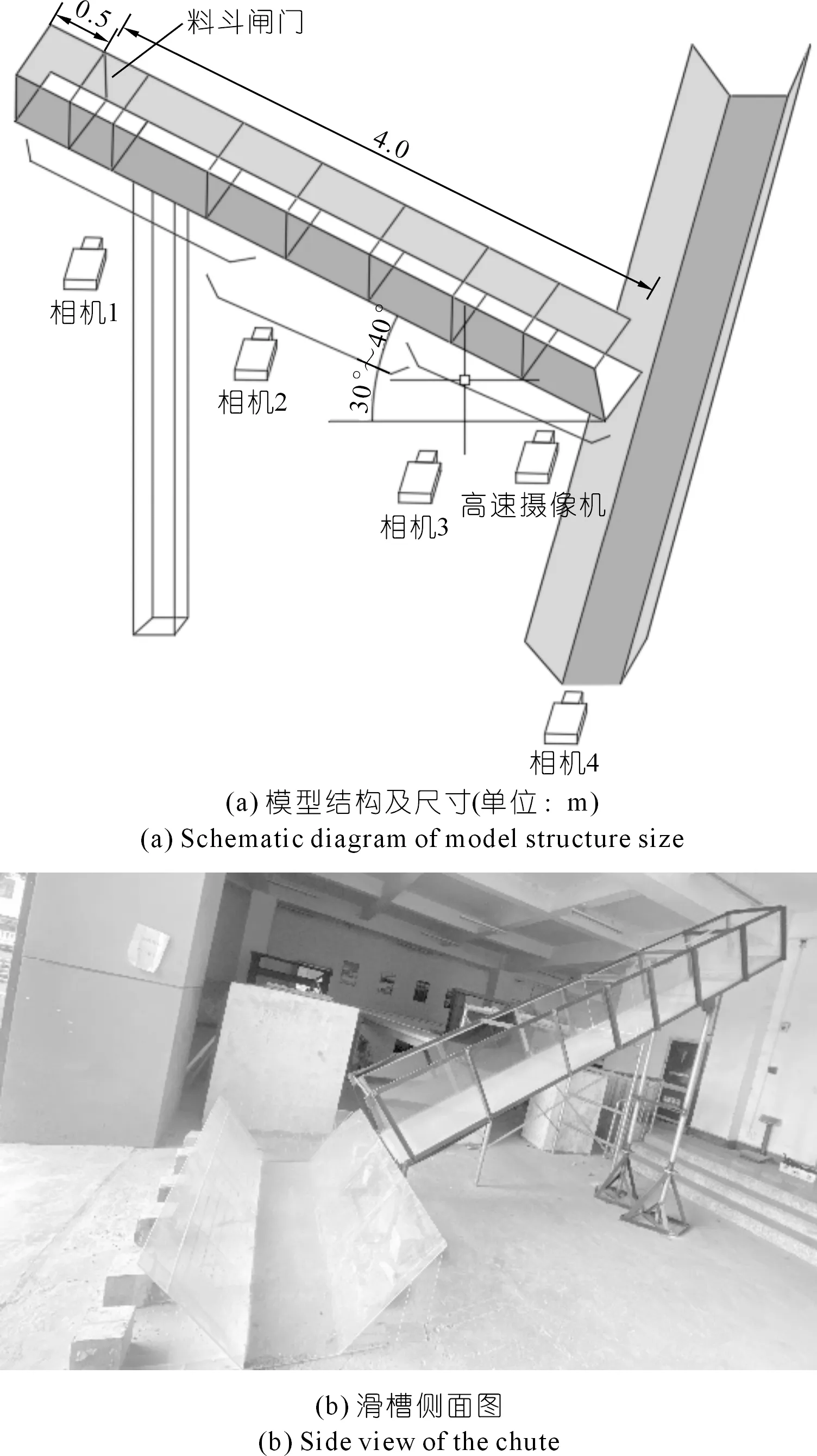
图1 滑坡物理模型装置Fig.1 Physical modeling test apparatus for landslides

1.2 试验材料及设计方案

基于滑坡物质组成的多样性，本次试验采用4种不同尺寸颗粒，分别为d=1～2 mm的细颗粒、d=3～5 mm的中细颗粒、d=6～9 mm的中颗粒、d=12～15 mm的粗颗粒以及细颗粒、中颗粒、粗颗粒的混合体，如图2所示。同时，考虑到部分实际滑源体存在明显分层现象，如石柱县龙井滑坡[24]、三峡库区多处出现的大型-特大型滑坡[25]，因此设置了水平分层的层状滑源体，如图3所示。其中，中颗粒(d=6～9 mm)在底部，细颗粒(d=1～2 mm)在中间，粗颗粒(d=12～15 mm)在上部，不同颗粒层间的接触面较为平整。另外，为了分析滑床坡度对运动过程及堆积特性的影响，斜槽坡度设置了32°及36°两种情况。本文共开展了24组试验，单粒径16组，分层的多粒径8组，具体试验方案见表1。

表1 试验方案设计Tab.1 Design of experiment schemes

图2 不同粒径试验材料Fig.2 Experimental material of different particle sizes

图3 滑坡体放置图Fig.3 Landslide placement diagram

试验开始前，将配置好的颗粒铺设在斜槽闸门后面，使滑体表面为水平面。接着，在滑槽同一侧面安装并调试4台录像机，相机1观察区域为滑槽前段，相机2观察区域为滑槽中段，相机3观察区域为滑槽后段，相机4主观察区域为水槽段，即滑体入河堵江阶段。另外，利用高速摄像机捕获距离斜槽出口30 cm区域内的滑体速度。为了获得完整、连续的滑体运动过程形态与数据，相邻录像机之间确保存在有交叉的共同摄像区域，并在斜槽闸门开启前已保持开启状态。最后，提起闸门，试验开始，滑体在重力作用下发生运动，当所有颗粒进入横槽后，一组试验结束然后对堰塞体的几何参数与颗粒分布进行量测。

2 试验结果分析

2.1 滑体运动过程分析

滑坡堵江运动过程可分为斜槽滑动阶段和入河堆积堵江阶段。本文以第4组试验为例介绍单粒径滑体运动过程。如图4(a)所示，当滑体位于斜槽前段，观察到提起闸门后位于滑体底部的颗粒会率先移动并牵引滑体前缘移动，随后滑体上部迅速掉落滑下。当滑体进入斜槽中段时，由于滑槽底部在两块亚克力板拼接处形成了起伏微小的滑面，滑坡体通过时出现了颗粒碰撞飞溅的现象。当滑体进入后段，速度明显加快，飞溅现象也更加显著。

其他各组单粒径滑体试验的运动过程现象与第4组相类似，但存在些许不同。如第1组滑体颗粒主要贴着滑槽底部运动，在滑槽中段起伏处以及出口处的飞溅程度较弱，而第2组滑体在这两处的飞溅高度则更大。分层多粒径滑体以第22组试验为例说明。其滑体运动状态与单粒径滑体相似，颗粒经过起伏滑面时也出现了飞溅、碰撞现象，出口处的飞溅以大颗粒为主，细颗粒主要沿着滑槽底板运动。同时，滑体前缘多为粗颗粒，细颗粒主要分布在滑体后缘，如图4(b)所示。

图4 滑坡体运动过程Fig.4 Movement process of landslide

2.1.1运动时间分析

将闸门提起的瞬间定为初始时刻t=0，滑体完全滑出斜槽出口的时间视为滑坡结束时间，当出口处颗粒呈现不连续状态作为滑坡运动结束的标志。各组滑体的滑坡运动时间如表2所列。

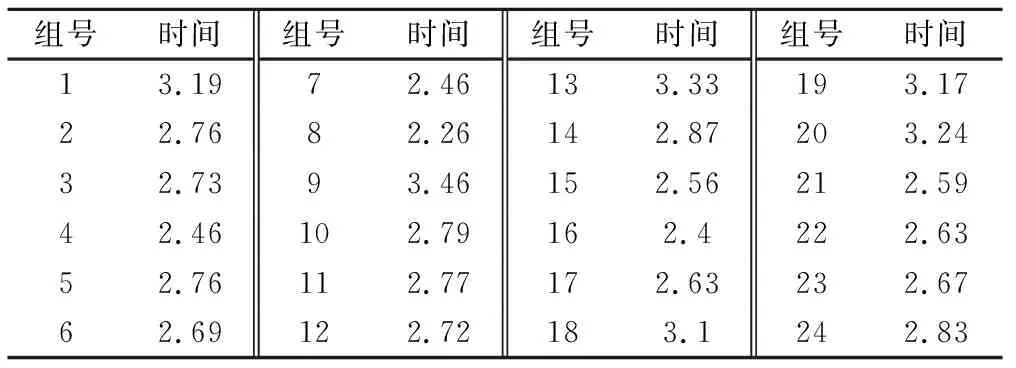
表2 非黏性物质滑坡运动时间统计Tab.2 Time statistics of non-cohesive material landslide movement s

如图5(a)所示，对于单粒径滑体，当滑床坡度一定时，滑体运动时间随着粒径增大而减小。这可能是由于颗粒在运动过程中，重力势能转换为动能，同时颗粒间相互碰撞飞溅产生冲击使后缘颗粒将能量传递给前缘颗粒，而这两种作用随着粒径增大而增强。细颗粒滑体运动时间最长，很可能是因为运动过程中细颗粒之间、细颗粒与滑槽底部之间的摩擦力最大，从而导致较大的动能损失。当坡度发生改变时，滑体运动时间随坡度增加而减小。这可能是坡度较小时，颗粒间因摩擦作用消耗的动能增加，后部物质的能量不能有效传递到前缘，导致运动速度减小。分层多粒径滑体的运动时间如图5(b)所示，滑体运动时间随着细颗粒比例增加而增大，随着坡度增加而减小，原因与单粒径滑体类似。

图5 运动时间随颗粒粒径的变化情况Fig.5 Movement time variation with particle size

2.1.2运动速度分析

滑体在滑槽前、中、后3段的平均速度为各段运动距离与运动时间之比。单粒径滑体的运动速度如图6(a)所示，各3段的平均速度均随粒径增大而增大，并在位于滑槽后段出口处达到峰值。分层多粒径滑体的运动速度如图6(b)所示，滑槽各段的速度均随着大粒径颗粒比例增加而增大，因此细颗粒比例最大的滑体速度最小。同时，滑槽前后两段滑体速度均随着坡度增大而明显增加；而在滑槽中段，滑体速度未随着坡度增大而增大，这可能是因为滑体经过起伏面颗粒滚动前进时碰撞作用程度增强，耗能过多、速度减小所致。

图6 平均速度随颗粒粒径、颗粒质量比及坡度变化情况Fig.6 Average velocity variation with particle size，proportion and slope

另外，采用混合水平正交方法对单粒径滑体的运动速度进行敏感性分析(见表3)。运用不同因素水平的平均值极差(记为R)来判别影响因素的敏感度大小，极差值大的因素对速度的影响大，是影响指标的主要因素；反之，极差值小的因对速度的影响小，是影响指标的次要因素。

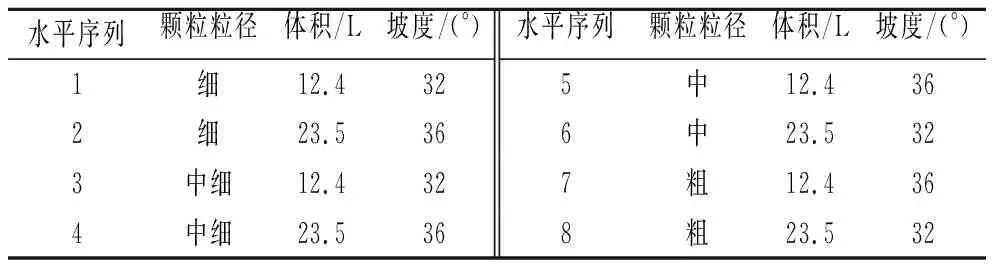
表3 正交分析因素及水平组合Tab.3 Factor and levels of orthogonal analysis

单粒径滑体极差分析结果如表4～6所列。结果显示，滑体在滑槽前段的速度受颗粒粒径影响最大，是主要因素，其次是坡度，最小是体积。滑体在滑槽中段及后段速度均受颗粒粒径影响最大，其次是体积、坡度。在滑槽前段，颗粒粒径决定着颗粒间相互作用及摩擦作用导致的能量耗散，从而影响滑体速度。此时，滑体的势能转换机制占主导作用，坡度对滑体速度的影响作用大于体积。在滑槽中后段，颗粒粒径对速度的影响与前段相似。此时，大体积下的滑体颗粒碰撞程度增强，滑体内部能量传递机制起主导作用，所以滑体体积对速度的影响作用大于坡度。

表4 影响因素各水平速度值Tab.4 The speed values of each level of influencing factors

表5 影响因素各水平速度平均值Tab.5 The average speeds of each level of influencing factors

表6 影响因素平均值极差分析Tab.6 Range analysis on average velocity of the influence factors

2.2 滑坡堰塞体特性分析

2.2.1单一粒径滑体的堵江堆积特性

堰塞体长度L、宽度W及高度H是堰塞体的3个关键几何参数(见图7)，对坝体稳定和溃决洪水大小具有重要影响，本文对这3个参数进行重点分析。

图7 堰塞体尺寸示意Fig.7 Schematic diagram of accumulation body size

试验结果表明，不同单粒径滑源体的堰塞体特性有所区别。从宽度向堆积形态看，细颗粒堰塞体扩散程度最小(见图8(a))，其次是中细颗粒与中颗粒(见图8(b)、(c))，扩散程度最大的是粗颗粒(见图8(d))。从长度向堆积形态看，细颗粒、中细颗粒与中颗粒均有凸起，且以细颗粒最明显；粗颗粒则出现较顺滑的倾斜面。细颗粒堰塞体最大坝高出现在滑槽一侧(见图8(a))，其余的出现在对岸(见图8(b)、(c)、(d))。可能原因是滑体颗粒之间存在能量传递[23]，而细颗粒的速度小、能量传递弱，撞击水槽底部后迅速停止运动，直接在滑槽一侧堆积；其他粒径滑体的速度较大、能量传递较强，滑体前缘撞击水槽底部后发生回弹并向对岸飞溅、堆积，其中以粗颗粒滑体最明显。

图8 单粒径物质堰塞体Fig.8 Landslide dam of single particle

堰塞体几何尺寸与粒径、体积、坡度的变化关系如图9所示。对于堰塞体长度L，其多随着体积和坡度增大而增大。坡度为32°时，小体积下的堰塞体长度随颗粒粒径变化幅度不大，大体积下的堰塞体长度随颗粒粒径增大而增大；坡度为36°时，小体积下堰塞体长度呈现出随颗粒粒径增大先略微增大后减小的变化规律，大体积下的变化规律与之相反(见图9(a))。这可能是因为中细颗粒相比细颗粒在出口处速度提高幅度不大，产生的冲击力相差不大，致使堰塞体长度L变化幅度只有轻微减小，而当滑体颗粒粒径增大，其回弹现象增强，导致堰塞体高度增加，从而堰塞体宽度也随之增加。对于堰塞体宽度W，其会随着坡度、体积、粒径的增大而增大，除细颗粒及中细颗粒粒径情况存在一定偏差(见图9(b))。这可能是由于细颗粒及中细颗粒滑体速度小，获得的动能少，没有强烈的扩散现象。对于堰塞体高度H，堰塞体高度随体积增加出现一定增幅。小体积下的堰塞体高度在同坡度下均随着颗粒粒径增大而增加，大体积下的堰塞体高度在同坡度下随着颗粒粒径增大先减小后增加，且在陡坡下的变化波动更明显(见图9(c))。

图9 堰塞体几何尺寸随坡度、体积及粒径的变化情况Fig.9 Variation of the geometric size of the accumulation with the slope，volume and particle size

为了进一步研究颗粒粒径、滑体体积等影响因素与堰塞体几何特性之间的量化关系，本文使用逻辑回归方法进行量化分析，其中建立不同参数之间定量关系的逻辑回归函数公式主要有加法公式和乘法公式。加法公式形式为

(1)

通过对本试验单粒径堰塞体几何尺寸数据处理分析，其中以堰塞体几何尺寸参数为因变量Yi，以试验设计方案中影响因素为自变量Xi，然后再以最小二乘法建立堰塞体几何参数和影响因素之间的模型。

所得模型的拟合程度可通过相关系数R2的大小来判断，R2的表达式为

(2)

基于试验数据选取相关参数，建立影响因素与单粒径堰塞体高度拟合模型如下：

Y=0.049+0.001∂+0.001V+0.005d

(3)

式中：Y为堰塞体高度预测值，∂为滑槽坡度，V为滑体体积，d为滑体颗粒粒径。

由相关系数可得，对堰塞体高度影响作用最大是颗粒粒径，其次是滑床坡度和滑体体积。此外，通过计算得出该模型R2=0.718，由于试验中粒径选择有一定范围，代入粒径数据时，会因为粒径大小选择结果影响预测结果，产生一定差值，但代入多组数据计算发现与实际测量相差均在0.005以内，说明该模型有较好的拟合程度。

2.2.2分层多粒径滑体的堵江堆积特性

同比例的分层多粒径滑体的堰塞体特性相似，以第17组试验为例进行分析。堰塞体整体形状呈扇形体，横向扩散程度较低，靠近滑坡侧的部位主要为细颗粒(见图10(a))。从平面和3个不同位置的剖面图(见图10)可知，细颗粒在坝体底部，粗颗粒在表面，表现为反粒序现象。可能的原因是细颗粒与滑槽底板接触面积大、流动性较差，同时颗粒间相互的碰撞产生了振荡筛分作用，使细颗粒穿过粗颗粒之间的间隙运移到滑体中下部。

图10 混合物堰塞体Fig.10 Landslide dam of mixed particle

分层多粒径堰塞体的长度变化规律如图11(a)所示。当改变坡度时，堰塞体长度与坡度无明显变化规律。当坡度为32°时，堰塞体长度随细颗粒、中颗粒比例增大而减小，随粗颗粒比例增大而略微增大；当坡度为36°时，则呈现出完全相反的趋势。这可能是由于细颗粒比例的增加，滑体动能少、没有强烈的回弹现象导致。堰塞体的宽度变化规律如图11(b)所示。随着滑床坡度增大，不同粒径比例下的宽度都有不同程度的增加。当坡度为32°时，宽度随细颗粒及中颗粒比例增大而减少，随粗颗粒比例增大而增大；当坡度为36°时，宽度随细颗粒及粗颗粒比例增大而减小，随中颗粒比例增大而增大。这可能是由于粗颗粒速度最大，其运动时间最短，颗粒间相互碰撞导致后缘颗粒可以有效传递动能给前缘，对水槽形成更大冲击力，宽度向扩散程度更强烈所致。堰塞体的高度变化规律如图11(c)所示。坡度为32°时，堰塞体高度随各粒径颗粒比例的增加而增大；坡度为36°时，堰塞体高度则随细颗粒及粗颗粒的比例增大而减小，随中颗粒比例增大而增大。堰塞体高度与坡度正相关。

图11 堰塞体几何尺寸随坡度和粒径的变化情况Fig.11 Variation of the geometric size of the accumulation with the slope and particle size

3 讨 论

本文研究了颗粒粒径、滑体体积、颗粒比例及坡度这几种因素对于滑坡体堆积过程及堆积特性的影响。在单粒径颗粒试验中，随着粒径增大，滑体颗粒撞击水槽底部产生的回弹现象增强，从而影响了堰塞体宽度方向的扩散。而分层多粒径堰塞体则出现明显的反粒序现象，其几何尺寸变化规律与不同粒径颗粒比例变化相关，具体表现为堰塞体宽度和高度都与细颗粒及粗颗粒相关联，堰塞体长度则与各粒径颗粒均相关，其中规律还需继续探讨。通过对高速摄像机在滑体运动过程拍摄的照片分析，发现后缘滑体会通过颗粒间碰撞的方式将能量传递给前缘滑体，从而增大前缘滑体的速度，这与葛云峰等[23]研究滑坡运动过程中的能量传递机制得出的结论相同。此外，本文多粒径的反粒序现象与王玉峰等[26]研究汶川地震产生的众多典型滑坡碎屑流案例得出的现象一致。

由于试验场地限制未能准确模拟实际地质环境，如本文滑槽底部平滑、无明显起伏、其坡度变化范围小；滑源体类型考虑单一，仅考虑碎屑物作为滑体来源，未考虑块体、黏性物质等其他材料，因此滑体滑动过程中的碰撞、破碎、筛分等现象未能在本试验中得到较好呈现；本试验没有考虑试验装置的尺寸效应，后续可通过开展不同尺度的模型试验进行探究。上述几个方面均对滑体速度、运动形态、堆积体特性等具有重要影响，需进一步完善，此外，本文分层多粒径试验数据较少，未能揭示影响因素与堆积体参数间的量化关系，后续也应在这方面加强研究，为更好预测堰塞体几何尺寸提供依据。

4 结 论

(1) 粒径组成、滑体体积及滑床坡度是影响滑体运动时间及速度的重要因素。滑体运动时间随着滑床坡度变陡、颗粒粒径增大而变短，随着滑体体积增加而变长。针对单粒径滑体，滑槽前段的运动速度影响因素重要性排为粒径、坡度、体积，中、后段为粒径、体积、坡度；针对分层多粒径滑体，前、后段滑槽的滑体运动速度主要受坡度影响，且随着坡度增大而增大，而中段的速度与坡度无明显规律。

(2) 单粒径堰塞体宽度及堰塞体长度在不同坡度下分别随滑体体积、颗粒粒径的增大而增大，且均对陡坡更敏感；堰塞体高度与影响因素关系的量化分析结果表明，影响程度最大的是颗粒粒径，然后是滑槽坡度和滑体体积。

(3)分层多粒径堰塞体的宽度和高度均随着坡度增大而增大，而长度与坡度无明显线性关系。同时，分层多粒径堰塞体存在明显的反粒序现象。