三维五向编织复合材料的一种改进细观三单胞建模

崔 灿 ，杨 化 奎 ，温 巍 ，魏 建 军

（江苏工程职业技术学院建筑工程学院，南通 226006）

0 引言

三维编织复合材料的空间结构具有周期性编织规律，这种规律给几何结构建模提供了可能。建立科学合理的模型是研究三维编织复合材料力学性能的前提。[1]20 世纪八九十年代，研究者们提出的用于预测复合材料性能的理论模型主要包括镶嵌模型（Mosaic Model）、纤维起伏模型、桥联模型、纤维倾斜模型、纤维塌陷模型、“米”字型单胞模型等。[2-5]21 世纪初，有研究者建立了内胞、面胞、角胞三单胞模型和细观单胞模型。[6-7]后续有人研究建立了参数化三维有限元实体模型，并进行了有限元验证。[8]英国诺丁汉大学MARTIN SHERBURN 设计开发的开源软件Texgen 通过输入编织工艺参数实现参数化实体建模，能基本实现任意纺织结构的几何建模。[9]2015年，有研究者建立了材料、结构一体化的计算机仿真平台，对三维五向复合材料的力学响应特性及细观损伤进行分析。[10]近年来，有研究者利用图像处理技术模拟了织物中各纱线的真实空间构型，实现了织物三维立体建模，并对织物相关性能进行了分析。[11-13]综上，随着计算机的发展，三维编织复合材料的几何结构仿真也逐渐精准。[14]目前的研究思路主要是先建立宏观、细观、微观三尺度下对应的几何结构模型，再基于纤维束的截面形状假设条件构建能够反映三维编织织物的复杂空间结构。

本文通过分析三维五向复合材料的编织工艺规律，重点研究三维五向编织材料中纤维束的运动轨迹及空间拓扑关系，建立了一种改进的细观三单胞模型。该模型采用可变截面参数化方法反映材料中纤维束横截面形状渐进变化以及纤维束间的相互挤压变形特征，进而确定各编织工艺参数。将编织参数的理论预测值与实测值进行比较，可以验证模型的适用性。

1 编织工艺及纱线运动轨迹

三维五向编织工艺是在三维四步法工艺基础上纵向地添加轴纱进行编织，工艺过程示意图见图1。图1 中编织纱以加圈的英文字母作为标识，如aa 表示第1 行第1 列，ab 表示第1 行第2 列……依此类推。加圈英文字母中间的带底色圆圈表示轴纱。在编织过程中，编织纱携纱器与轴纱携纱器有固定的编织走向，编织纱随携纱器按照四步法进行横向和纵向的运动，而轴纱随携纱器只进行横向往复运动。再经打紧工序操作，整体编织织物得以收紧，结构达到稳定。如此循环操作便可获得具有矩形截面的三维五向编织织物的预制件。此处，将织物经历1 个编织循环沿纵向方向增加的长度设为1 个花节长度h。纱线随编织运动会逐渐呈现规则的周期变化规律，且纱线在不同区域的截面形状以及扭转程度也各不相同。由此可按照这种变化规律对三维五向编织预成形体的表面、棱角和内部三区域进行面胞、角胞、内胞的三单胞划分，划分情况如图2 所示。

图1 四步法三维五向编织工艺过程

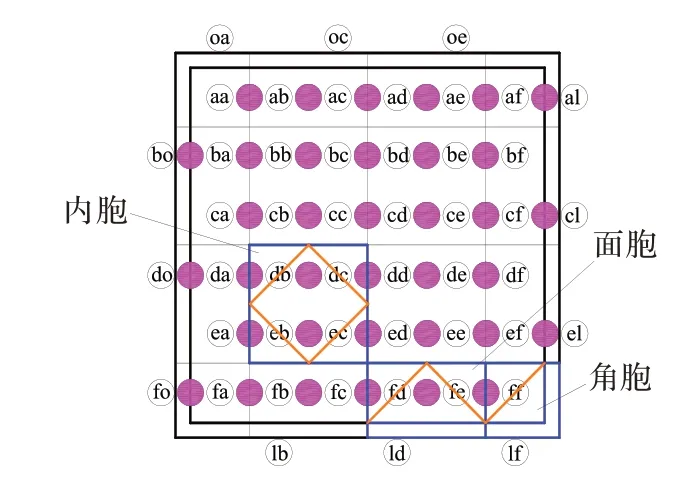
图2 三维五向编织复合材料三单胞划分

由三维五向编织工艺的分析可知，织物的纱线由于编织和打紧工序而呈现一种相互挤压缠绕的形态，从而导致纱线在空间结构中各处的截面形状以及扭转弯曲程度不同，最终造成三维五向编织材料整体空间构型比较复杂。然而，纱线又不是毫无规律地相互缠绕，而是依照一定的编织工艺进行运动，因此纱线的运动轨迹又具有周期性的变化规律。图3、图4 和图5 所示分别为三单胞中1 条编织纱运动轨迹的水平投影图、侧视图和三维立体视图。

图3 三单胞中1 条编织纱的空间运动轨迹水平投影图

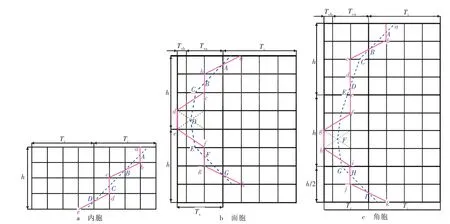
图4 三单胞中1 条编织纱的空间运动轨迹侧视图

图5 三单胞中1 条编织纱的空间运动轨迹三维立体视图

1) 图3a、图4a、图5a 中，a→b→c→d→e为内胞编织纱（编号db）的运动轨迹，打紧后简化为直线ABCD，与Z轴（即纵向）夹角为γ，其投影与xy平面（即水平投影面）夹角约45°。

2) 图3b、图4b、图5b 中，a→b→c→d→e→f→g→h为面胞编织纱（编号fd）的运动轨迹，其中a→b→c和f→g→h的运动轨迹与内胞编织纱的运动轨迹一致，打紧后分别简化为直线AB和FG；而c→d→e→f的运动轨迹中，由于d→e处（即纱线在前一步的编织位置）停顿一步，纱线仅在Z轴方向下移h，经打紧后，该段纱线出现90°的扭转，故将该段纱线简化为以C、D、E为控制点连接的空间曲线，并分别在点C和E处与直线AB和FG相切，曲线的切线与Z轴的夹角为θ。

3) 图3c、图4c、图5c 中，a→b→c→d→e→f→g→h→i→j→k为角胞编织纱（编号 ff ）的运动轨迹，其中a→b→c和i→j→k的运动轨迹与内胞编织纱的运动轨迹一致，打紧后分别简化为直线AB和HI；在c→d→e→f→g→h→i的运动中，先后在d→e和g→h处各出现一次停顿，经打紧后，该段纱线出现180°的扭转，故将该段纱线简化为分别以C、D、E和E、F、G为控制点连接的两条空间曲线，并在点E处相切，在点C和G处与直线AB和HI相切，曲线的切线与Z轴的夹角为β。图6 为三单胞中轴纱的运动轨迹示意图，纱线由1→2→3→4→5→6 在X方向往复运动，打紧后简化为直线ab，平行于Z轴。

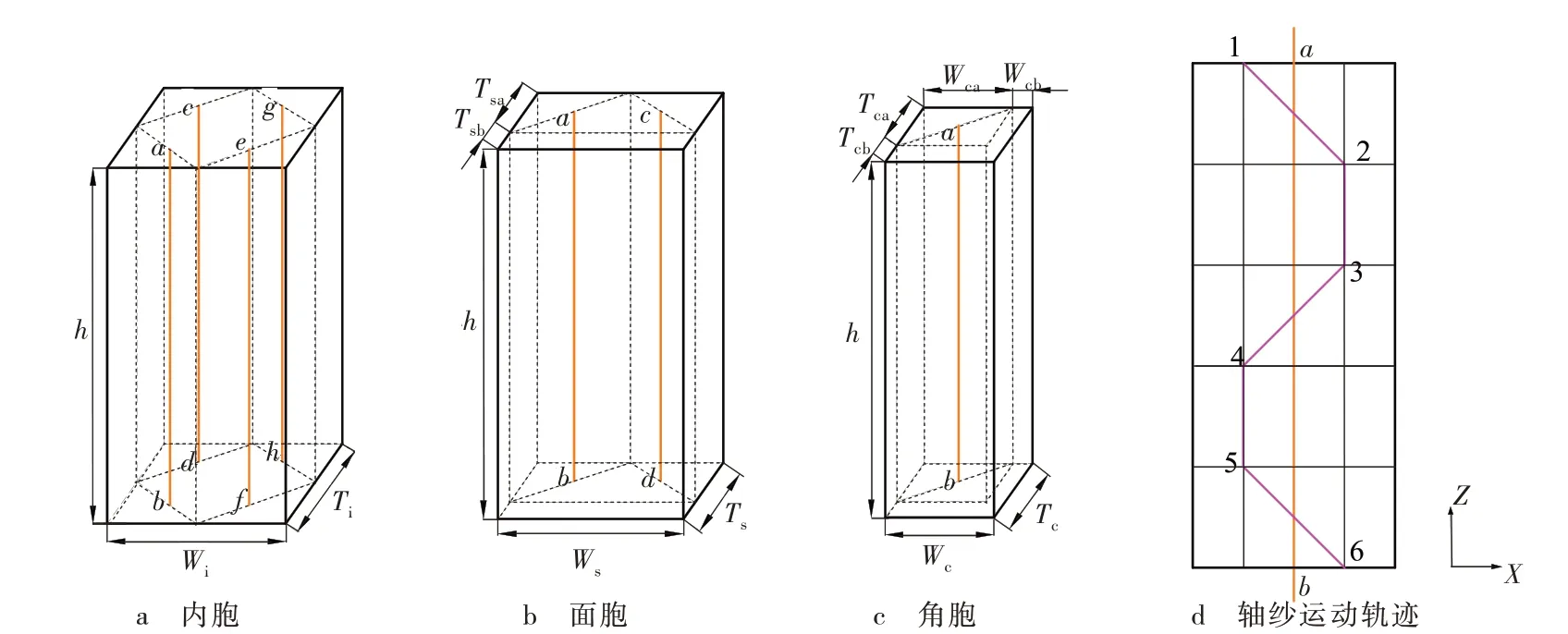
图6 三单胞中轴纱的空间运动轨迹示意图

内胞、面胞、角胞内轴纱的运动轨迹完全一致，所包含的轴纱根数分别为4 根、2 根、1 根。

2 三单胞模型的基本假设及结构参数间关系

建立模型前做出以下基本假设：

1) 整体编织及打紧工序稳定，所有纱线为同一种材料，且不考虑材料缺陷等问题存在。

2)编织纱、轴纱的截面形状分别为六边形和正方形，且不同单胞中各纱线具有不同的纱线填充因子。

3) 因考虑到三单胞模型中每条纱线被挤压后产生的变形程度各不相同，故假设内胞中各纱线横截面形状保持不变，面胞和角胞中编织纱和轴纱的横截面形状变化各有差异，其中面胞和角胞中编织纱的横截面分别沿运动轨迹以正弦曲线发生渐进变化，轴纱的横截面积等比例缩小，变化比例系数为ϕsb、ϕcb、ϕsz和ϕcz（下标sb 表示面胞中的编织纱，cb 表示角胞中的编织纱，sz 表示面胞中的轴纱，cz 表示角胞中的轴纱），整个模型中纱线即便有接触也并不相交。

编织纱和轴纱的横截面尺寸见图7。图7 中，a、b分别为编织纱横截面内切椭圆的长半轴长度、短半轴长度其中γ为内部编织角，r为轴纱截面尺寸因子，rb为轴纱横截面边长，编织纱横截面积Sb=（6+4r）b2cosγ，轴纱横截面积Sz=r2b2。三单胞几何结构模型中内胞的长Wi、宽Ti，面胞的长Ws、宽Ts，角胞的长Wc、宽Tc计算式分别见式（1）、式（2）、式（3）。

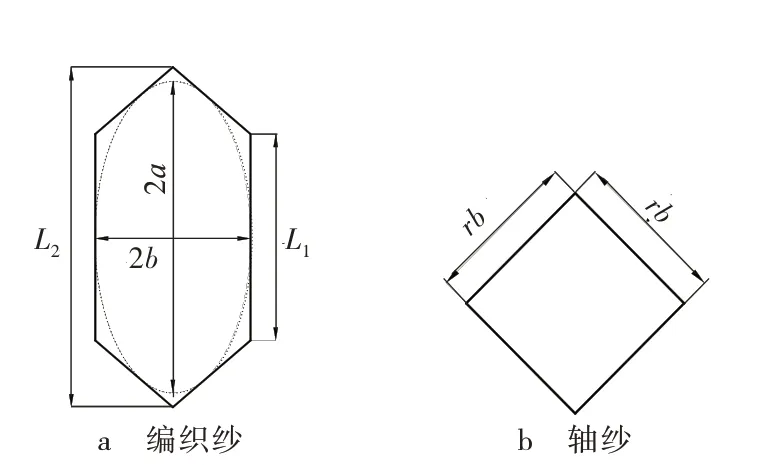
图7 编织纱与轴纱的横截面尺寸

式（2）、式（3）中Tsa、Tsb、Wca、Wcb、Tca、Tcb如图8 所示。

图8 三单胞的曲线细观几何模型

各编织角关系为：tanγ= 3 tanθ=3 tanβ=（其中γ为内部编织角，θ为表面编织角，β为棱角编织角，α为机械编织角）。

图8 所示为三单胞的几何结构模型示意图。依据模型中材料整体尺寸与单胞结构的参数关系，即可获得不同排布规律、不同编织角以及不同纤维体积分数的三单胞实体模型。

三维五向编织复合材料预制件整体的长Wx、宽Ty见式（4）。

式（4）中n为纱线排布列数，m为纱线排布行数，bx、by分别为长度方向和宽度方向上编织纱的短半轴长度。

单胞模型中编织纱的短半轴长度b=（bx+by）/2，预制件的花节长度，纱线填充因子ε、纱线等效直径Dy的计算式见式（5）。

式（5）中Ω 为纱线横截面面积，λ 为纱线线密度，单位为g/m，ρ为纱线体积密度，单位为g/cm3。

经几何分析可得内胞体积Ui、编织纱体积Yib、轴纱体积Yiz以及内胞纤维体积含量Vif的计算式，详见式（6）。

式（6）中εib和εiz分别为内胞中编织纱和轴纱的纱线填充因子。

面胞内包含7 根编织纱，而每根编织纱的运动轨迹简化情况各有不同，为计算方便，对每根纱线进行逐一编号（如图8b所示）。经过几何分析可得面胞的体积Us、编织纱体积Ysb、轴纱体积Ysz以及面胞的纤维体积含量Vsf的计算式，详见式（7）。

式（7）中ϕsbi和ϕsbj为面胞中每段编织纱的横截面积变化因子；εsbi和εsbj为面胞中各段编织纱的纱线填充因子；εsz为面胞中轴纱的纱线填充因子；i表示面胞与内胞连接处编织纱横截面积变化较小处的编织纱线段编号，i=1，2，3，…，7；j表示面胞最外层编织纱横截面积变化最大处的编织纱线段编号，j=1，2，3，4，5。

依照面胞中编织纱的分析方法，将处在1 个机器编制循环中角胞内的4 根编织纱分别编号（如图8c所示）。经几何分析可得角胞体积Uc、编织纱体积Ycb、轴纱体积Ycz以及角胞纤维体积含量Vcf的计算式，详见式（8）。

式（8）中ϕcbi和ϕcbj为角胞中每段编织纱的横截面积变化因子；εcbi和εcbj为角胞中各段编织纱的纱线填充因子；εcz为角胞中轴纱的纱线填充因子。i表示角胞与内胞连接处编织纱横截面积变化较小处的编织纱线段编号，i=1，2，3；j表示角胞最外层编织纱横截面积变化最大处的编织纱线段编号，j=1，2，3,4，5。在不考虑行列奇偶性的情况下，三单胞分别占整体结构的体积分数的计算式见式（9）。

式（9）中Vi、Vs、Vc分别为内胞、面胞和角胞占整体的体积分数，m为纱线排布的行数，n为纱线排布的列数。因此，三维五向编织复合材料总纤维体积分数Vf的计算式为：Vf=VifVi+VsfVs+VcfVc。

3 三单胞模型的建立及验证

本文基于MATLAB R 2016a 软件和Creo 6.0.2.0 软件平台建立三单胞模型，根据结构参数间关系计算三单胞模型尺寸、编织纱和轴纱的横截面形状及尺寸，并确定纱线在运动轨迹上各控制点的空间位置坐标。

内胞模型的编织纱和轴纱都以直线形式简化，只要确定纱线运动轨迹上的两个控制点空间位置坐标，就可建模获得；面胞和角胞编织纱的截面形状呈现渐进变化趋势，且编织纱在空间结构上呈现出90°和180°的扭曲形态，为在模型中构建这种空间曲线的形态变化，同时保证曲线部分能与直线部分光滑衔接，避免在曲线直线交界处出现尖角，且因纱线即便接触也不相交，本文采用Creo 软件对面胞、角胞内编织纱曲线部分进行参数化建模，所得模型的视图见图9、图10。图11 给出了29.4°编织角下的三单胞结构模型。

图9 面胞内编织纱曲线部分模型

图10 角胞内编织纱曲线部分模型

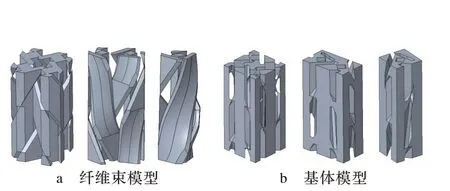
图11 29.4°编织角下三单胞实体结构模型

将模型与实际材料试样的横截面视图、表面视图、三维视图进行对比（如图12、图13、图14 所示），结果发现：三单胞纱线模型横截面整体均呈现周期性形态变化，内部存在较多近似矩形截面形状的空位。模型的外表面纱线呈现规则曲线形态，内表面呈现规则直线形态。纱线模型与基体模型共同组合成为三维编织实体结构模型。然而，对比真实试样，材料整体虽较为紧密，但仍存在较少孔洞（即缺陷），这是由于在树脂固化成型工艺中树脂未能完全浸透材料而引起的。材料表面纱线形态与模型外表面形态较为相似，这表明模型能够较为真实地模拟试样的整体空间形态。为进一步验证模型的正确性，将计算所得的参数预测值与试样的实测数据（见表1）进行对比，结果见表2。由表2 可见：模型预测值与试样实测值比较吻合，且在织物排列结构的行数m和列数n相等时（编织角22.3°、26.5°时），两者吻合度最好，表明模型适用性好，且对织物排列行列相等的情况尤为适用。

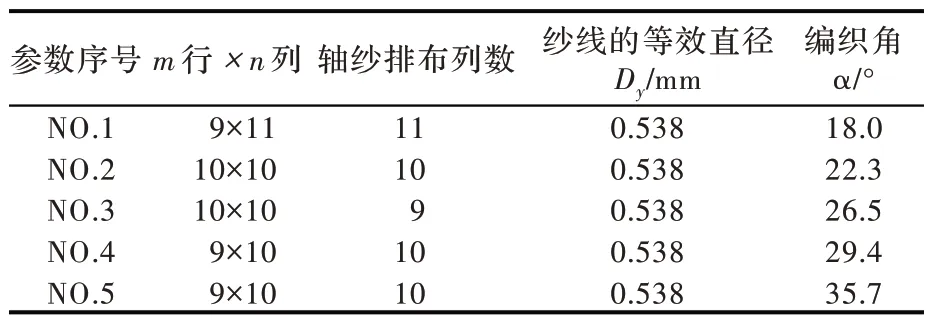
表1 三维五向编织复合材料试样的工艺参数值

表2 三维五向编织复合材料试样的模型预测值与实测值比较

图12 三单胞组合纱线模型与实际材料的横截面视图

图13 三单胞组合纱线模型与实际材料的表面视图

图14 三单胞组合纱线模型与实际材料的三维视图

4 结论

本文建立的细观三单胞模型在考虑纤维束横截面积渐进变化的情况下实现了参数化建模，更真实地反映了编织纱90°和180°的弯曲扭转特征，且模型的理论预测值与实测值较为吻合。主要结论如下：①内胞中纱线的空间轨迹为直线，面胞中纱线和角胞中纱线的空间轨迹为直线和曲线的组合，并且曲线和直线光滑衔接。依托Creo 6.0.2.0 软件中的参数化方程式建模，真实反映了材料内纤维束因挤压变形而成的相互交织形态。②模型给出了整体尺寸与基本编织参数的关系，为获得不同排布情况、不同编织角以及不同纤维体积分数下的三单胞实体模型提供了借鉴。