基于优先级的车间排产算法的研究

杜 芝

（青岛前哨精密机械有限责任公司，山东 青岛 266110）

1 引言

机械制造业多以多品种小批量的离散型生产方式为主，随着ERP和MES在公司的深度应用，在推动公司发展的同时，也涌现出不少问题。ERP只能根据生产订单生产零件级的生产计划建议，缺乏对资源的精细化管控，而MES仅记录生成过程中的各类关键信息，企业生产现场的各类关键信息不能被有效利用，不能满足公司日益增长的业务发展需求。

车间接收到零件生产订单的时候，就需要进行车间的排产。通俗的讲，排产就是将零件各工序按照一定的规则或者方法分配到设备上，使生产有序进行。然而如何进行各工序排序以及与设备的匹配会直接影响到车间设备利用率、物料流转、生产进度和交付率等较多方面的指标。所以一个公司对车间作业进行管理和控制，保证生产各环节有条不紊地进行，需要有效解决车间排程问题。这样一来，公司在接单时就可以根据客户需求准确迅速回复交货期。通过对车间排产的应用可以客观分析出生产环节的卡脖子问题，对突如其来的订单修改和必要插单，找到最合理的时间安排和解决方法；还可以测算最大产能，指导公司科学接单，争取利润最大化。因此，在企业数字化转型快速发展的现阶段，设计开发一套科学、合理、快速且有效的排产算法是重中之重。

2 排产现状

机加车间目前排产不是基于生产订单，且没有一定的规则和方法，导致订单不能按期完成，有些加工完成的零件也不是现有订单所需，导致库存量增大。由于零件种类多，仅加工件就有300余种，且批量小需经常切换加工任务，再加上零件工艺路线复杂、设备分配变化大，给生产现场管理工作带来极大的不确定性，其突出问题是生产现场在制品多，产品生产周期长且进度不透明，设备利用率不高，给产品按期交付带来较大隐患。

本研究以车间生产排程问题为基础，对实际生产过程的现状进行研究，在满足约束条件的前提下，梳理出符合车间现状和发展的优先级排程策略。此处的“优先级”包含两层意思：①生产周期长且交货期短的零件具有较高的排产优先级；②针对每一道工序，有许多台可用设备，在满足车间忍耐度的情况下尽可能的排在优先级最高的设备上，文中会详细说明。用这个方法可以将零件各工序分配到相应的设备上，并根据得到的排序确定各个零件的开始和结束时间，建立各零件任务全周期、执行全过程的生产计划，减少排程的随意性与盲目性。

3 建模

3.1 基础数据

车间排程问题能够描述为以下数学模型：①有a个待加工零件，加工这些零件可使用的机器有m台；②每个零件有特定的加工工艺路线；③在加工每道工序时可用设备列表是已知的，一个工序可对应一个或多个设备，设备根据实际情况分优先级；④每道工序开始前的准备时间和单件加工时间已作为基础数据给定。

3.2 约束条件

车间排产约束条件：①假定在同一时间，同一台设备不能加工多于一种零件；②假定在同一时间，相同零件的同一道工序只能选择一台设备加工；③假定每个工件的每一道工序一旦开始加工就不能停止，直到结束；④假定不同零件的工序之间不存在任何约束关系；⑤假定可用设备列表里的设备均为可用设备，不考虑设备故障和保养。

4 算法实现

排产算法的主逻辑如图所示。首先，初始化建模时候所有的基础数据，包含所有零件的工艺路线、所有工序的准备时间、单件加工时间及每一个工序对应的可用设备列表，有些数据在MES中已经存在的，可以直接拿来用。根据ERP运行完MRP后提供的零件生产计划建议确定零件生产订单，该生产订单含有零件种类、数量和交货期，程序会遍历所有待排产工序，并标记为待排产。

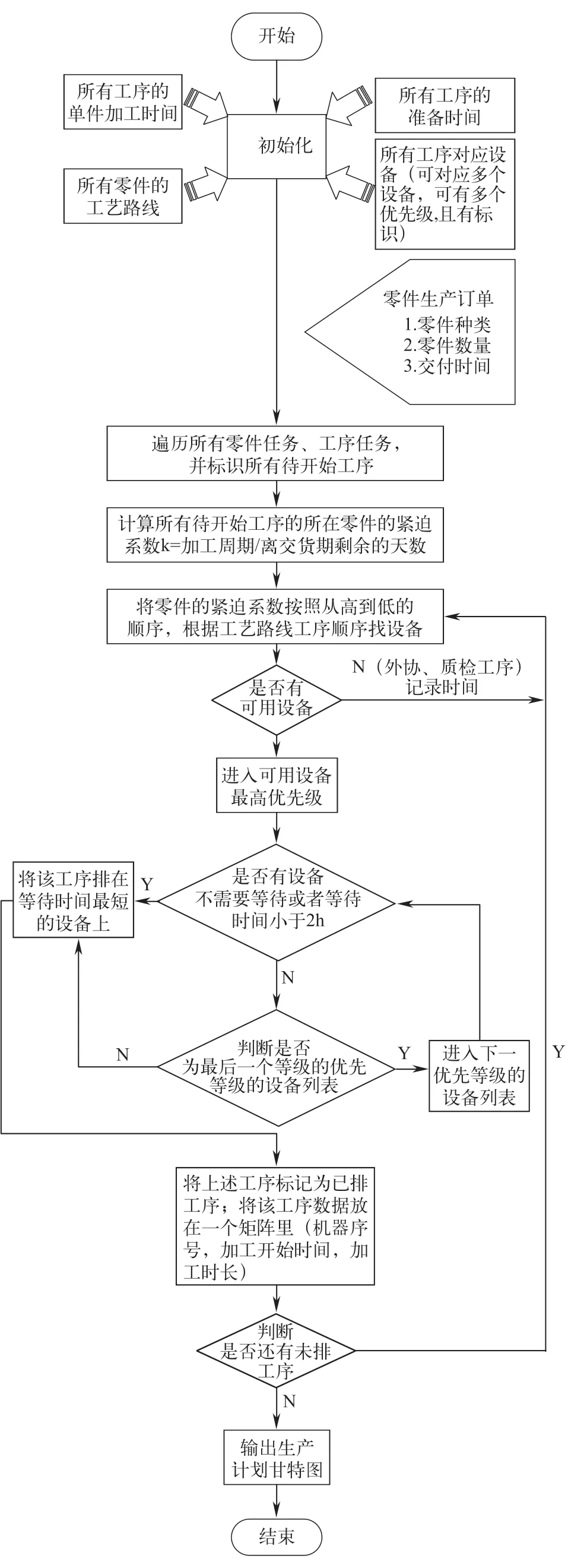
图 优先级排产主逻辑图

然后计算待排产零件的紧迫系数k[1，2]，并做出修改。式中，i为某零件工序顺序值，p为某零件工序总数，t为该某工序开始前的准备时间，ti为某工序单件加工时间，n为该零件待加工数量，公式分母表示的是该零件任务的加工周期。T1为交付时间，T为排产开始时间，公式分子表示离交货期剩余的时间。

当k＞1时，表明任务紧迫，所有的任务都为其让步时，也不能完成工作任务，只有通过资源协调、增加班次或者委外加工等方式才能保证交期；当k=1时，表明在理想情况下，任务恰好可以在交期结束；通常情况下，公司所接的订单k＜1的，但是值越大，表示任务越紧急，该任务就有越高的排产优先级，这就为车间排产提供了依据。

将待排产零件任务按照降序排列，从第一个零件开始，按照加工工艺路线所有工序进行排序，再让每一道工序去找其对应设备[3]。

根据零件的工序与其对应的可用设备列表来看，大多数的工序都对应着不止一台设备，而且这些设备都能够完成该工序的加工，但也存在着优先级问题，比如P工序可用设备为M1，M2和M3，三台设备都可以完成次工序，但如果在M1有空闲的情况下，车间计划员多会将A1在工序在M1上进行加工，因为M2对于加工A1这类工序来说是大材小用，而M3上可能因为经常加工某个工艺，上面的工装不方便拆卸，拆卸需要花费大量时间。这样可以认为在工序P的可用列表里M1的优先级为1，M2和M3的优先级为2。当然，针对不同的加工工序其可用设备列表里的设备可能有更多层级的优先级划分，这在基础数据中均会表示出来。

从紧迫系数最大的零件的第一道工序开始，寻找设备。如果其所对应的优先级最高的设备不需要等待或者等待时间在2h（假设整个车间的最大等待忍耐度是2h）以内，则选择等待时间最小的设备将其排产；如果所在优先级对应的设备均要等待2h以上，进入下一个优先级的对应设备；如果遍历完所有级别的可用设备，等待时间均在2h以上，则选择最高优先级中等待时间最短的一台设备进行排产。遍历完紧迫系数最高的零件的所有工序，再按照零件的紧迫系数的降序遍历第二个零件的所有工序，以此类推，直到所有的待排产工序都排产完毕[4]。

5 算法分析

该优先级排产算法能够将工件按照一定的规则排在机器上，对产品交期的预测有一定的指导作用。缺点是不能考虑使得某一指标最优，如在制品最少，设备利用率最高，产品生产周期最短等。也没有考虑车间日历的情况，但是就目前排产的行业现状来看，本身就不存在最优的算法，需要在今后的探索中基于上述要素进行迭代优化。

6 结束语

本文提出的优先级排产算法是基于我公司生产现状的一种策略，是根据机加车间各类资源的限制和实际需求的一种排产算法。在算法中提出了紧迫系数和车间忍耐度的概念并用复杂公式进行量化，该算法充分考虑到了订单的生产周期和交货期，以及工序与机器的最佳适配，还可以通过优化兼顾设备的利用率、研试制件及重点客户等指标。因为车间生产状况的复杂性和多变性，会使得自动计算得出的排产结果并不能完全契合于车间的实际情况，计划管理人员手动修改调整排产结果也是必要的。截止目前，该排产算法已进入车间应用阶段，并达到预期效果。