动车组齿轮箱传感器优化布置

赵翔彦,马 洋,张学礼,校 艳,吴健强

(1.西安交通工程学院机械与电气工程学院,陕西 西安 710300;2.中国铁路兰州局集团有限公司兰州西车辆段,甘肃 兰州 730050)

我国铁路客运的发展方向是高速化,随着运行时速的大幅度提升,动车组列车的工作环境愈加复杂,为了保证列车安全运行,对列车运行状态进行实时数据监控至关重要,尤其是对动车组牵引传动系统的监控。而齿轮箱作为动车组牵引传动系统的主要零部件之一,它是牵引电机和轮对之间动力转换的连接装置,起着传递转矩、调节转速的作用。为了更准确地监测齿轮箱振动信息,需要选择合适的传感器布置位置。虽然齿轮箱箱体有振动监测传感器,但只能监测箱体表面的振动信息,无法获得内部齿轮和其他部位的振动信息。齿轮箱位于动车组转向架底部,安装位置隐蔽，难于拆卸,工作环境恶劣,且在工作过程中受到多种激励影响,振动产生位置和原因比较复杂,监测器安装位置有限,因此需要优化齿轮箱传感器布置方案[1]。可信度较高的传感器布置方案使齿轮箱运行状态尽在掌握,可对动车组齿轮箱进行精确的故障诊断和预测寿命。齿轮箱作为动车组动力系统重要部件,在列车运行中主要受到3个方面的激励载荷:一是轨道不平顺和车轮磨耗等原因造成轮轨冲击的外部激励,通过轮对传递到齿轮箱;二是牵引电机转轴形成谐波转矩的外部激励;三是齿轮啮合刚度变化造成的周期性振动的内部激励,通过传动轴传递给齿轮箱[2-4]。齿轮箱的故障诊断一直以来是机械行业的研究热点,获取齿轮箱振动状态也有多种方法,如振动监测法、温度检测法、油液分析法等。但温度监测法、油液分析法等具有局限性,很难精确地诊断故障位置,而振动监测法可以获得更多的有效信号,方便于故障诊断[5-6]。

目前,国内外学者对传感器优化布置进行了深入研究,分析了动车组牵引传动系统的振动特性。袁雨青等[7]在运行列车的齿轮箱箱体上布置传感器采集振动信号,发现车轮20阶磨耗产生的振动与齿轮箱固有频率接近,易和齿轮箱产生共振；Kammer[8]提出有效独立法,以有限元模型为基础,从全部自由度中迭代筛选对目标贡献度较小的自由度,以信息矩阵为基础保留对目标模态线性贡献度较大的自由度；刘伟等[9]提出有效独立-加速度幅值和有效独立-模态动能两种方法,既保证了信号不会相互干扰,又保证了采集到较准确的信号源;杨广雪等[10]在武广客运专线对箱体进行线路试验,获得箱体在新轮和磨耗轮两种状态下的振动特性,表明箱体在列车磨耗轮状态下的加速度振动幅值要低于新轮状态,一定程度磨耗的轮对会改善齿轮箱箱体的振动特性；常程城[11]在齿轮箱箱体易产生裂纹处布置传感器,获取齿轮箱箱体振动特性,利用振动频谱分析方法归纳振动传递规律,结果表明齿轮箱箱体低频振动来自轴箱振动传递,高频振动主要受齿轮啮合振动影响；范军等[12]选取两种齿轮箱在同一位置布置加速度传感器,在相同工况下分析测点的时频域振动特性和高频振动特性,得出齿轮箱箱体上的振动与线路条件有着密切的关系。

综合相关文献,大多数学者主要采用有效独立(EI,effective independence)法和模态动能(MKE,modal kinetic energy)法研究分析传感器在机械零部件上的测点位置布置。这两种方法在机械故障诊断的选取测点中应用比较广泛,但二者都有优缺点。EI法虽然能够保证所选测点对目标模态贡献的线性独立性,但是无法保证测点位于动能较大的区域,从而导致结构动态特性信息的丢失；MKE法虽然考虑了各自由度对目标模态的平均动能贡献,却忽略了某一自由度下对目标模态的影响,不能保证目标模态之间的线性独立性。据此,综合分析EI法和MKE法的优缺点,针对EI法引入比例系数的概念,用模态振型比例系数评价两测点间的信息独立程度,提出了一种能够同时满足所选测点模态可测性和避免信息冗余性的测点优化布置算法,提出了基于振动模态的置信准则评价测试点选取方法的优劣,并与EI法和MKE 法进行了比较。结果表明:采用比例系数-有效独立法研究分析齿轮箱结构的振动模态信息,是一种更优的测点布置方法,更能精确地诊断出齿轮箱的故障特征。该方法有助于准确分析齿轮箱箱体的振动特性,为高速列车齿轮箱的故障诊断和健康预测提供理论依据。

1 问题描述

1.1 齿轮箱结构组成

齿轮箱结构如图1所示。齿轮箱是动车组牵引系统中重要的零部件之一,结构组成有:主从动齿轮副、轴承、力矩传动轴和外部齿轮箱箱体。它的主要作用是连接牵引电机与轮对,将牵引电机输出的低扭矩通过齿轮转化为高扭矩转矩,驱动动车组高速运行。

图1 齿轮箱结构Fig.1 Gearbox structure

1.2 齿轮箱常见的故障

齿轮箱安装在动车组转向架底部,工作环境恶劣,工作强度高,长期处于高速旋转状态,箱体内部齿轮之间长期啮合工作会有较严重磨损,轴承长期高负载工作会导致内外圈配合间隙过大、轴不对中、箱体产生裂纹等故障。根据线路运行数据统计,齿轮箱常见故障发生位置占比如下:齿轮54%,轴承21%,传动轴14%,箱体11%。由此可见齿轮和轴承是齿轮箱装置发生故障的主要零部件。齿轮长期啮合高速转动很容易产生磨损故障,出现齿面化学腐蚀(见图2(a) )、断齿(见图2(b))、磨损(见图2(c))等情况。产生故障的原因有:齿轮制造误差、齿轮装配误差和较复杂的工作环境等。

图2 齿轮故障状态Fig.2 Gear status

2 齿轮箱传感器优化布置

2.1 齿轮箱模态分析

为了更准确检测到齿轮箱的运行数据,更早发现齿轮箱的故障,对轮箱传感器布置位置进行优化改进。选取齿轮箱作为研究对象,其三维模型如图3所示,其材料为HT150,密度7 100 kg/m3,泊松比为0.25,弹性模量为1.5×1011Pa。

图3 齿轮箱模型Fig.3 Gearbox model

在分析齿轮箱模态时,因其结构特点,网格单元选取四面体比较适宜。选取网格大小时,若过于密集会导致传感器采集的信号有重复情况,造成信号失真。因此,要保证选取网格略大于传感器信号测取区域,该模型的网格的大小定义为20 mm。考虑齿轮箱安装在动车组转向架底部,为使试验数据更具精确性,模态分析以齿轮箱下箱体底部4个螺栓孔作为固定支承点,添加固定约束。根据齿轮箱传感器布置方案,模态阶数对试验结果有很大影响,在实际结构监测中并不能完全得到结构模态数据,只能尽可能得到频率较明显、位置较平整处的模态信息,因此采用不完全模态信息进行齿轮箱传感器布置。试验数据表明:模态数过多会造成频率相似,计算量过大,导致数据求解稳定性变低;若模态数过少,会导致模态频率跨度过大,结果不具有线性标准性,影响传感器布置。因此选取前7阶模态作为试验数据,它具有良好的线性相关性,满足传感器布置要求。最终将齿轮箱划分为7 998个节点,3 818个单元。采用Lock lanczos运算法提取模态参数,齿轮箱的前7阶模态的分析结果见表1。

2.2 传感器布置方案确定

(1) 比例系数-有效独立法 有效独立法最初是由Kammer提出的一种传感器优化布置方法,其主要是从所得测点集合出发,利用算法语言对所得节点数进行迭代筛选,保留目标模态动能响应较大的节点,剔除对目标模态动能响应较小的节点,从而使有限的传感器尽可能多的获得所测目标信号[13-14]。有效独立法根据模态叠加原理,从模态坐标最小二乘估计的估计误差的协方差最小化角度出发,通过求解模态矩阵所构造的Fisher矩阵的特征方程,构造矩阵E从而通过对角线迭代计算的方式,最终得到传感器布置位置。

表1 齿轮箱模态分析结果

设传感器输出响应为Us,即

(1)

(2)

其中:E为数学期望;Q为Fisher信息矩阵。

假设噪声相互独立且每个传感器的统计特性都相同,则

(3)

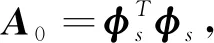
因此,试验构造的矩阵E为

(4)

E是幂等矩阵,对角线上第n个元素表示第n个测点对矩阵φs秩的贡献度,即对矩阵A0的贡献度,所以E表示所测节点候选传感器位置的独立分布状态,E对角线上的元素表示相应节点所在传感器对模态矩阵线性无关的贡献。得到矩阵E,以对角线上各元素节点振型进行排序,迭代筛除对角线响应小的节点,保留响应大的节点,最终保留具有突出特性的传感器布置节点。使用此算法可以有效保留模态矩阵线性无关性,使得齿轮箱原有结构特性能最大限度的保留。

传统有效独立法可以有效地估计结构的振动特性,但是它忽略了两个待选测点有相似的Fisher信息矩阵的情况。虽然每个待选测点对模态矩阵线性独立性的贡献都很大,但是如果他们的信息矩阵基本相同,那么选择这两个测点和其中一个测点得到的结构模态信息是相同的,这就产生了冗余现象。针对这一问题,定义模态振型比例系数为两个节点模态向量间的余弦值[15],用来评价测点之间的信息独立性,即

(5)

其中:φi和φj分别为第i和第j个测点提供的模态振型,即模态矩阵的第i行和第j行,N为模态截断数目。对于布置方案中任意两个测点,均满足

0≤lij≤1,∀i,j。

(6)

当lij=0时,说明两个测点提供的信息矩阵是相同的,则选择其中的一个测点就可以表示结构模态信息;当lij=1时,两个测点提供的信息矩阵相互独立。

(2) 确定传感器位置 根据上述所提取的齿轮箱振型信息,考虑齿轮箱上下箱体结合、内部齿轮啮合、轴承连接处和齿轮箱结构本体应力集中等因素,采用比例系数-有效独立法计算,从而使传感器布置位置尽量靠近振动频率较高的节点上,综合上述因素影响,设定比例系数-有效独立法初始测点群。算法流程如图4所示。

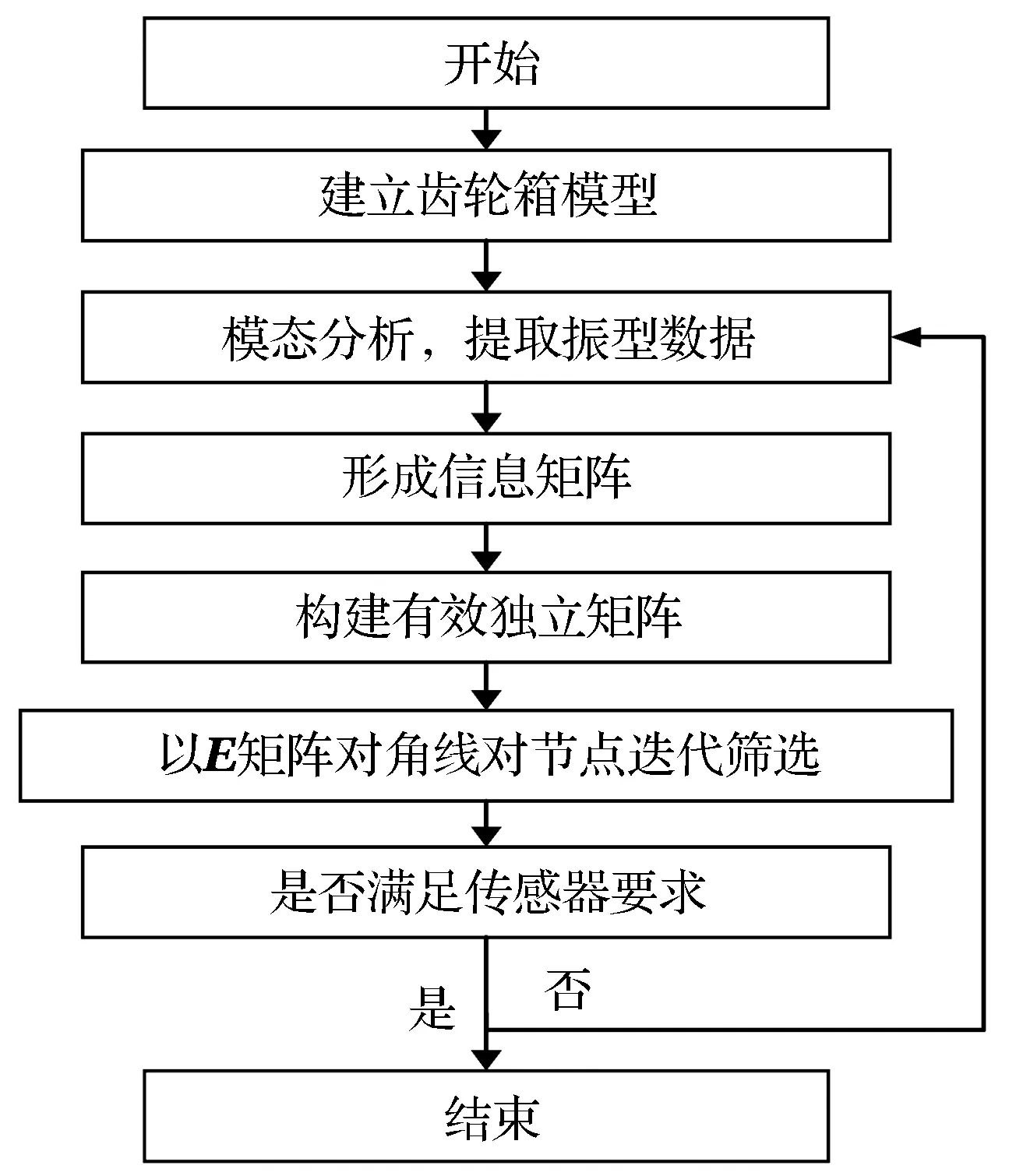
图4 传感器测点选取流程Fig.4 Flow chart of sensor measurement point selection

通过齿轮箱试验模态数据,分别提取各模态对应的振型数据,形成Fisher信息矩阵,运用比例系数-有效独立法筛选所有节点。结合齿轮箱箱体有效空间情况,针对形变总量中变形比较明显的区域,从7 998个节点中筛选出6个节点作为传感器布置位置,分别是主动轮上方、上箱体中部、输入端、上箱体中部靠近输出端、从动轮上方和齿轮箱箱体边应力集中点处。传感器初选位置如表2所列。

根据齿轮箱模态形变总量图,传感器布置位置如图5所示。2号点在齿轮箱上箱体中部位置,满足第4阶段模态形变最大处;3号点和4号点分别在从动轮顶部以及从动轮输出端盖处,满足第5阶段和第6阶段形变应力集中点;6号点在靠近从动轮侧上下箱体连接处,满足第3阶段、第6阶段、第7阶段形变最大处。

表2 传感器初选位置

3 齿轮箱传感器布置方案评价标准

3.1 模态置信准则

模态置信准则(MAC,modal assurance criterion)应用于传感器布置评价方案中,是目前比较常见的评价标准[16]。根据机械结构振动特性,对它分析选择自由度时要尽可能使模态向量的空间夹角更大。这使原有结构模态信息最大化保留,对试验分析结果影响较小,在对结构做振动特性试验时,必须使传感器布置位置采集到的模态信息保持相互线性独立性。在实际机械结构振动力学测试中,获取的目标自由度远远小于结构本身所具有的自由度,且采集的数据受测试环境中噪声和传感器精度的影响,不易保证所测得的模态矩阵之间的正交性,因此会对相距较近模态造成线性相关,使结构模态信息丢失,影响识别精度。

图5 传感器布置初选测点Fig.5 Sensor arrangement primary measuring points

在布置传感器过程中,考虑节点之间获得的结构模态相互线性独立,Carne认为衡量各模态独立性最简单的方法是构造模态保证准则矩阵[17-20],其计算公式如下:

(7)

MAC矩阵中非对角元素表示各模态间的独立性,MACij=0时,表示i模态向量和j模态向量正交;MACij=1时,表示i模态向量和j模态向量重合,故要求MAC矩阵中非对角元素越小越好,从而提高各模态的可分辨性。由于理论与实际存在差别,模态信息保证矩阵中的非对角元素不可能都趋于零,Carne认为在机械复杂结构中,非对角元素最大可取至0.25。

3.2 传感器布置方案评价

MAC矩阵中非对角线元素平均值和最大值也是评价模态相关性的指标,Fisher信息矩阵是评价外界因素对测点模态干扰影响的指标,其均值越小,幅值波动越平稳,则说明所选测点模态动能越稳定。试验所得到的矩阵MAC数据组为

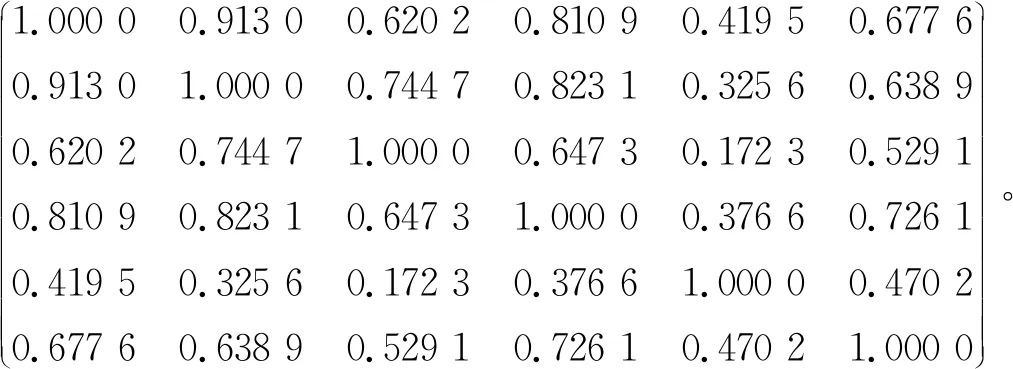
MAC矩阵也称为振型相关系数,是振型向量之间的点积,计算得到的标量值在0～1之间,MAC矩阵见图6。

图6 MAC矩阵Fig.6 MAC matrix diagram

模态置信度矩阵中非对角元素越小,说明各阶计算振型独立性越好,传感器配置效果越好,反之则各阶计算振型相关性越大,传感器配置效果越差。根据MAC数据和MAC矩阵图,表明试验数据采集良好,数据之间没有明显波动,且数据相互之间有良好的线性独立性,模态矩阵中元素最小值为0.172 3,符合试验中动车组齿轮箱传感器优化布置方案要求。

4 结论

为了解决动车组齿轮箱结构健康监测中的传感器优化布置问题,综合考虑EI法和MKE法的优缺点,针对EI法引入比例系数的概念,用模态振型比例系数评价两测点间的信息独立程度,提出了一种能够同时满足所选测点模态可测性和避免信息冗余性的测点优化布置算法,同时提出了基于振动模态的置信准则评价测试点选取方法的优劣,并与EI法和MKE法进行了比较研究,验证了所提方法的可行性和有效性。得到如下结论:

(1) 建立齿轮箱三维模型以及有限元模型,采用Block lanczos运算法提取模态参数,提取模态振型信息,构成Fisher信息矩阵,利用比例系数-有效独立法对齿轮箱节点迭代筛选出传感器布置位置的6个最优节点。

(2) 采用模态置信准则(MAC)作为标准评价齿轮箱传感器布置方案,根据MAC矩阵图,表明试验数据采集良好,数据之间没有明显波动,且数据相互之间有良好的线性独立性,模态矩阵中元素最小值为0.172 3,符合试验中动车组齿轮箱传感器优化布置方案要求。

(3) 比例系数-有效独立法是一种更优的测点布置方法,用其研究分析齿轮箱结构的振动模态信息,能更加精确地诊断出齿轮箱的故障特征。该方法有助于准确分析齿轮箱箱体的振动特性,为高速列车齿轮箱的故障诊断和健康预测提供理论依据。