基于Wolffersdorff模型面板堆石坝应力应变数值计算

黄小华，吴乐海

(福建水利电力职业技术学院，福建 永安 366000)

在全球能源紧缺，碳中和政策的背景下，新能源的开发已变得越来越受关注。利用流量和落差发电的水电能源能实现零碳排放，符合当下的能源要求。作为当前坝工界主要坝型之一的面板堆石坝因其具有施工方便，投资相对较低，在高度提升情况下占地较小等优点，在水利工程中得到广泛应用[1]。由于面板堆石坝防渗的主体是混凝土面板，受力主体为堆石料，若在设计阶段对堆石料变形预测不当，后期可能会导致面板脱空、拉裂等情况的发生，从而造成严重渗漏，还有可能造成溃坝的风险，因此对堆石料应力应变的研究显得尤为重要[2- 3]。由于堆石料具有剪胀剪缩、非线性等性质，因此在堆石料的应力应变分析中选择一个合理的本构模型至关重要。目前，弹塑性本构模型和非线性弹性模型是国内外坝工界对混凝土面板堆石坝力学分析的2大主要本构模型。但是，这2类本构模型都不能很好地反映堆石料剪胀剪缩、非线性等力学特征，在考虑颗粒破损方面也较为欠缺，且忽略了屈服面与应力路径的关系[4- 6]。近年来，国内外有学者将亚塑性理论应用到无黏性土的本构模型研究中，提成各种亚塑性本构模型，该类模型能弥补传统本构模型的不足，能更好地反映堆石料特殊的力学特征。

本文简单介绍Wolffersdorff亚塑性本构模型及其有限元计算方程。并将该亚塑性本构模型应用于福建仙游抽水蓄能电站下库混凝土面板堆石坝力学数值计算中，同时将该模型计算的数值成果与沈珠江双屈服面弹塑性本构模型计算的数值成果进行对比。旨在验证该本构模型应用于面板堆石坝应力应变分析的可行性。

1 Wolffersdorff亚塑性本构模型

亚塑性本构模型理论是在寻求颗粒骨架之间的级配性质的基础上[7]，以连续介质力学理论，通过建立应力率与应变率的张量函数，在函数中加入其他本构理论，如非线性理论、考虑颗粒破损[8]、湿化效应[9]、剪胀性[10]等情况，对亚塑性本构模型进行不断完善，从而得到适用于堆石料的本构模型。Wolffersdorff[11]对砂砾料进行研究，在前人研究压缩性模型的基础上引入Druker-Prager临界准则，加入了临界状态函数“F”，使得模型在模拟颗粒破坏状态下的应力应变关系更加真实。Wolffersdorff模型表达式见式(1)所示。

(1)

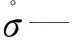
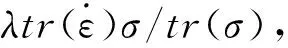
(2)

模型中参数α和β的求取，吴长彬[14]在常规三轴压缩试验下得到与平均压力ps有关，为简化其关系，引入参数k1、b1、k2、b2，如式(3)—(4)所示：

α=k1ln(T33/pα)+b1

(3)

β=k2ln(T33/pα)+b2

(4)

简化后的参数共11个：λ、hs、n、φc、ei0、ed0、ec0、k1、b1、k2、b2，使得参数获取更加容易，根据福建仙游抽水蓄能电站的筑坝材料试验报告数据[15]计算得到主堆石料和次堆石料的模型参数见表1：

2 亚塑性材料矩证模量[D]的确定

有限元的理论是将整体进行分割成单元，将单元利用虚功原理外力功与应力功平衡，列出平衡方程，再对单元进行叠加求得整体平衡方程。单元的平衡方程如下：

(5)

式中，{δ*}e—节点虚位移；{ε*}—虚应变列阵，可表示为{ε*}=[B]{δ*}e；{σ}—单元应力列阵{σ}=[D][B]{δ}e。

[K(D)]{δ}={R}

(6)

式中，{δ}—整体节点位移列阵；{R}—整体结点荷载列阵；[K]—整体劲度矩阵；[D]—材料矩阵模量。因此上式有限元平衡方程的求解取决于[D]，由率型本构方程[16]：

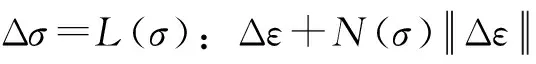
(7)

(8)

因此，可得到矩阵[D]的表达式为：

(9)

对式(8)进行展开：

(10)

表1 模型参数表

提出式(2)中的Δε，结合式(10)，可得到矩阵模量[D]分量：

(11)

式中，下标i=1，3;j=1，3，从而可得整体的劲度矩阵[K]求解出有限元平衡方程(6)。

3 亚塑性本构模型在工程中的应用

3.1 工程概况及计算方法

为了验证改进的Wolffersdorff亚塑性本构模型应用于面板堆石坝应力应变分析的可行性，本次选用的工程案例为福建仙游抽水蓄能电站下库混凝土面板堆石坝，该大坝的基本参数如下：坝高75.1m，坝顶宽度8.0m，坝长263m，前坡坡比：1∶1.4，后坡坡比：1∶1.35，混凝土面板的材料特性参数取γ=24.0kN/m3、μ=0.167、E=2.8×107kPa。大坝的断面图如图1所示，对大坝有限元网格剖分如图2所示。

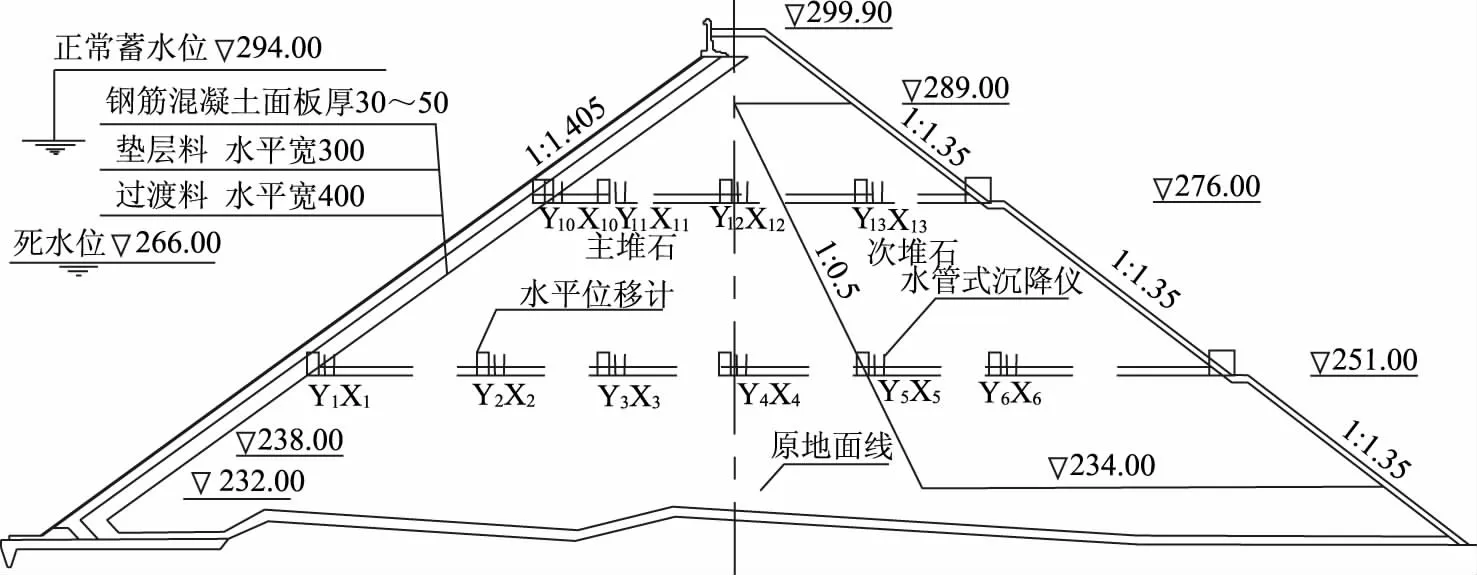
图1 大坝断面图(单位：m)

图2 大坝有限元网格图

对式(6)式非线性有限元方程的求解，采用中点增量法，对仙游面板堆石坝的下库大坝进行分28级加载，施加本级荷载的一半力{ΔR}i于结构，得到本级的平均值，使得结构的精度得到提高，中点增量法示意图如图3所示。

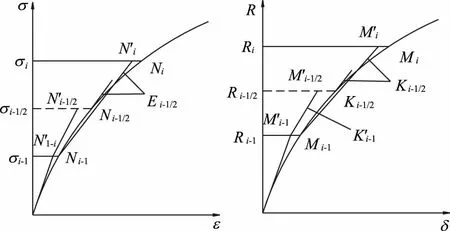
图3 中点增量法

3.2 计算结果分析

3.2.1坝体应力应变结果分析

在对福建仙游抽水蓄能电站下库面板堆石坝的三维有限元分析中，堆石料的本构模型分别采用改进的Wolffersdorff亚塑性本构模型和沈珠江弹塑性模型，计算工况为竣工期和正常蓄水期。2种本构模型计算的坝体应力及变形结果见表2，各种工况下的水平位移、垂直位移及大小主应力等值线图如图4—7所示。其中，水平方向的位移以向下游为正，垂直方向的位移以向下为正，应力以压为正。

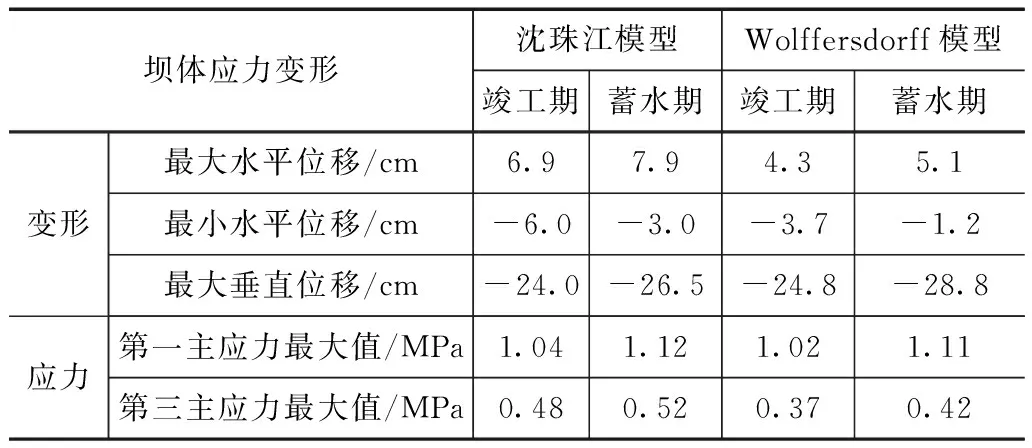
表2 不同模型坝体应力应变结果对比

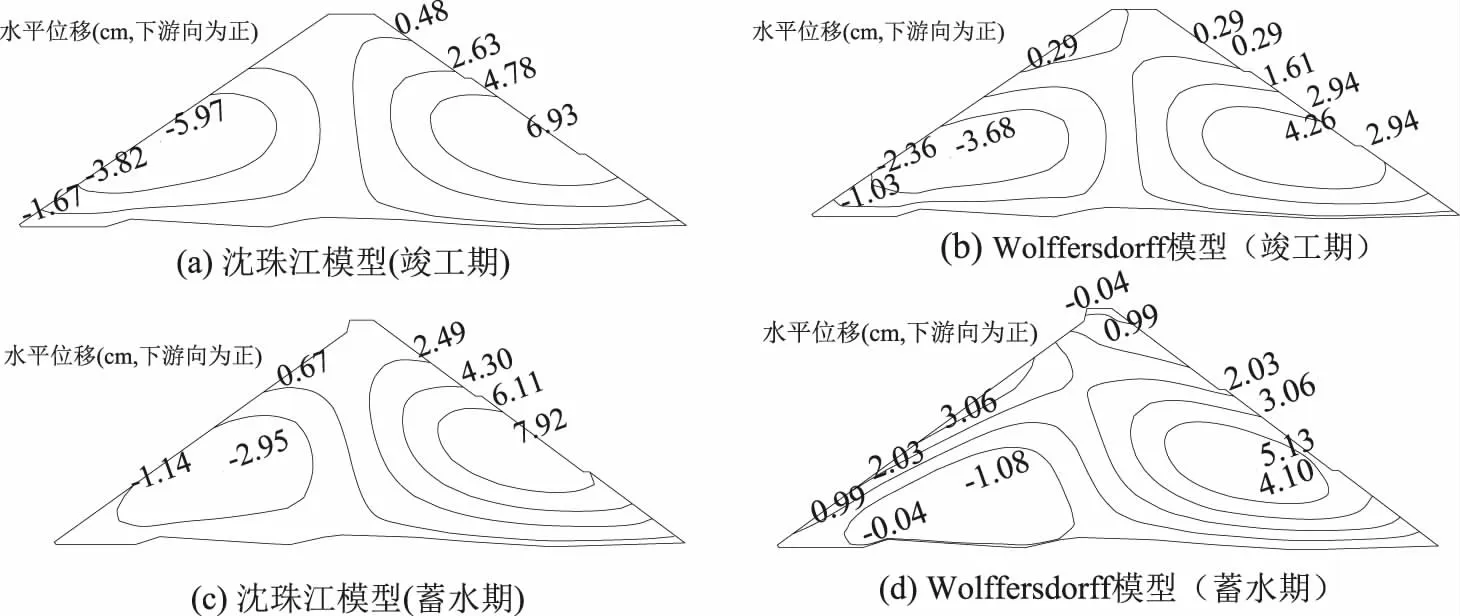
图4 大坝河床断面水平位移等值线分布图

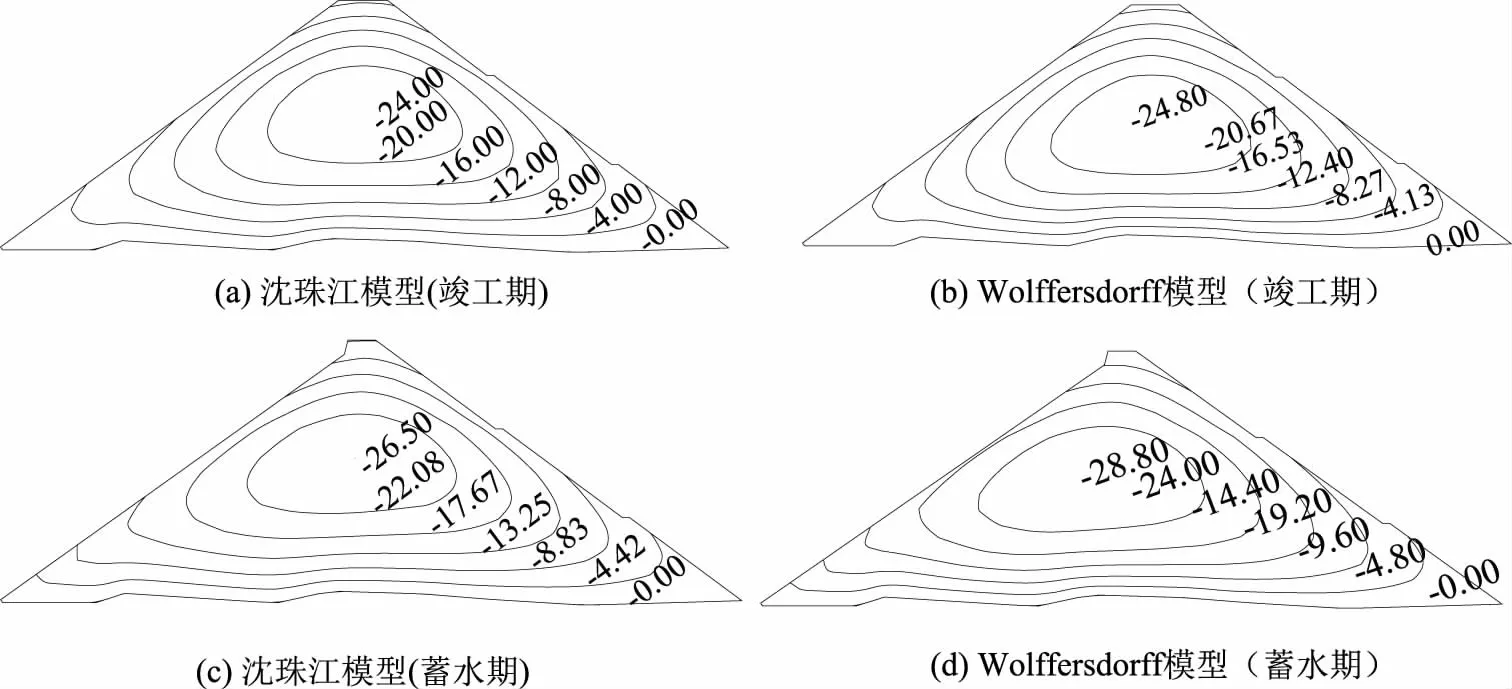
图5 大坝河床断面垂直位移等值线分布图

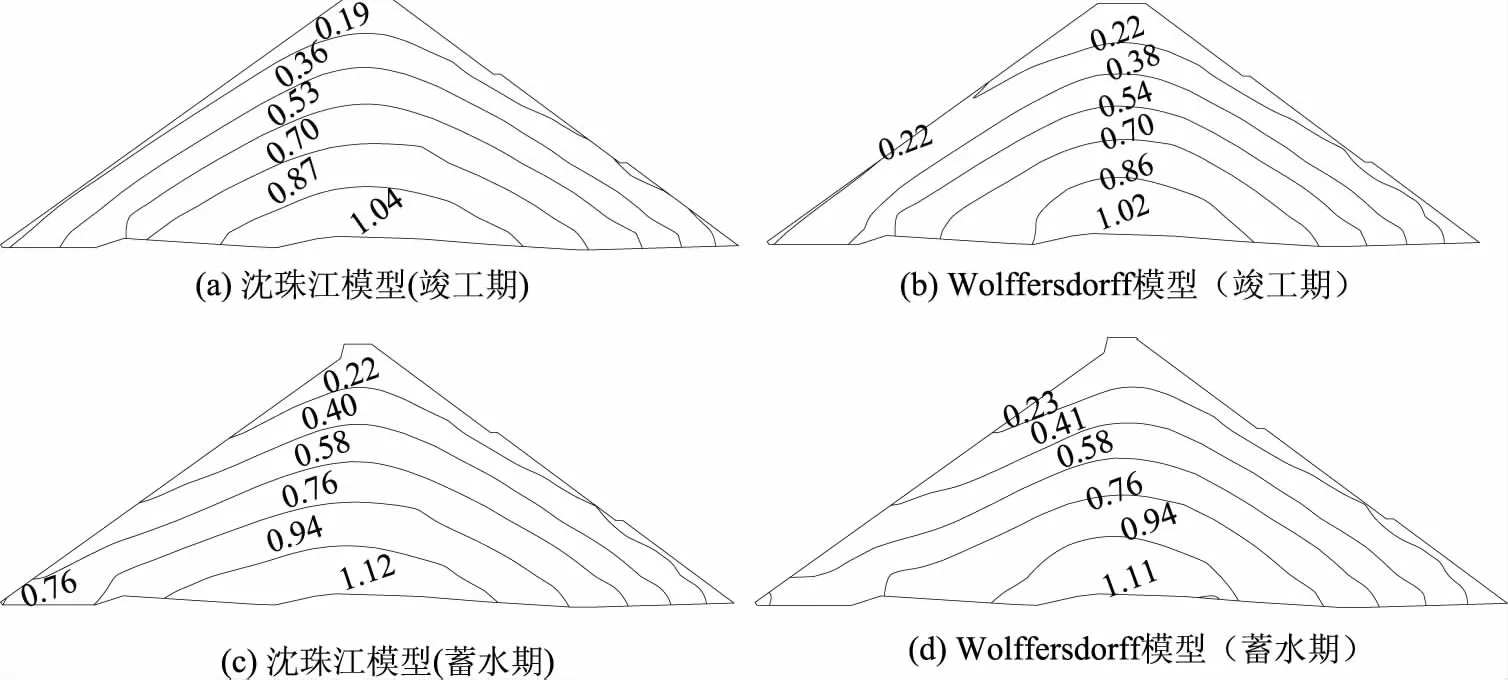
图6 大坝河床断面第一主应力等值线分布图

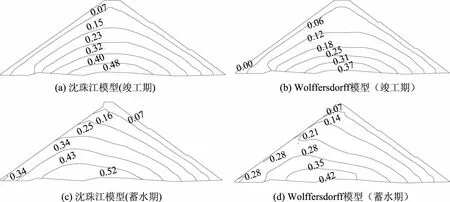
图7 大坝河床断面第三主应力等值线分布图

由表2可以看出，竣工期Wolffersdorff模型计算出的最大水平位移为4.3cm，最大垂直位移为24.8cm，沈珠江模型最大水平位移6.9cm，最大垂直位移24.0cm。竣工期Wolffersdorff模型计算出的最大水平位移比沈珠江模型更大，增幅达到60%，2种本构模型计算出的最大垂直位移较为接近，约占坝高的0.33%；蓄水期Wolffersdorff模型最大水平位移5.1cm，最大垂直位移28.8cm，沈珠江模型最大水平位移7.9cm，最大垂直位移26.5cm。蓄水期Wolffersdorff模型计算出的最大水平位移比沈珠江模型增大55%，最大垂直位移的比较中，Wolffersdorff模型也比沈珠江模型更大2.3cm。从计算结果上看，2种模型位移的计算结果偏差不大，在水压力作用下，下游向的水平位移比上游向的水平位移来的更大。从位移等值线分布云图分析，两者模型分布特征基本相似，在堆石的自重作用下，坝体垂直位移最大值出现在1/2坝高处，并向四周逐渐减小。水平位移大致成对称性，呈下凸上凹形状，略有不同在于蓄水期Wolffersdorff模型坝体上游侧中上部位指向下游侧，沈珠江模型指向上游侧。

由表2可知，竣工期Wolffersdorff模型第一主应力最大值为1.02MPa，第三主应力最大值为0.37MPa，沈珠江模型相应的应力为1.04，0.48MPa，从计算结果可以看出，在竣工期，2种本构模型第一主应力计算数值非常接近，第三主应力二者差值为0.11MPa，从应力的等值线分布图来看，两者模型的应力分布规律相似，大小主应力均出现在大坝的底部。蓄水期Wolffersdorff模型第一主应力最大值为1.11MPa，第三主应力最大值为0.42MPa，对比沈珠江模型为1.12、0.52MPa，2种模型计算结果非常接近。从图7还可以看出，2种模型的第三主应力最大值较竣工期均有往上游移动的趋势。

3.2.2面板应力应变结果分析

蓄水期2种本构模型计算的面板应力变形计算成果见表3、如图8—9所示，规定应力以压为正，变形以下游向为正。

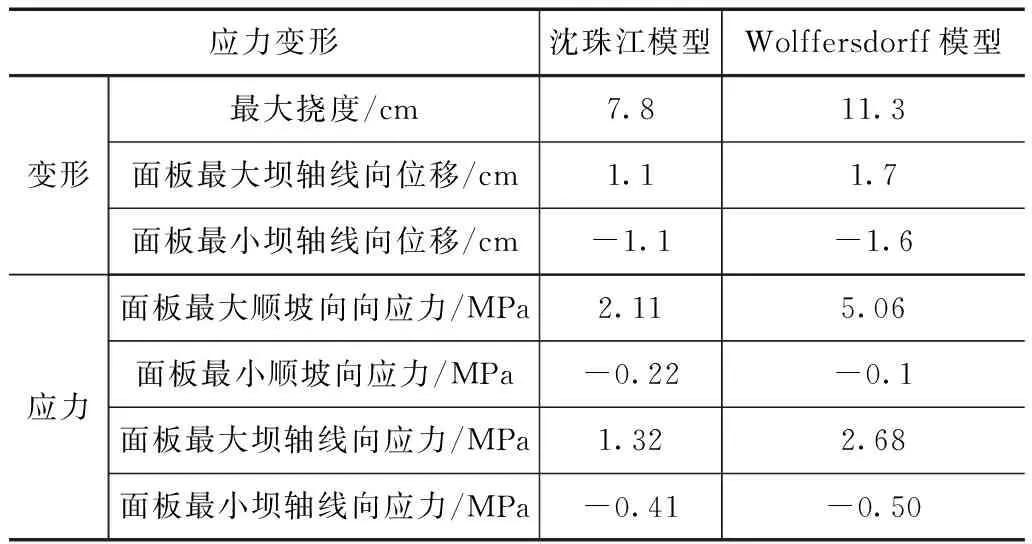
表3 不同模型蓄水期面板应力应变结果对比

如图8蓄水期面板位移云图所示，Wolffersdorff模型和沈珠江模型挠度位移和轴线向位移分布规律相同，最大挠度部分均出现在坝体1/2～1/3区域，并从坝体两侧向中间逐渐变大。从云图可以看出，混凝土面板最大扰度的位置与坝体堆石料最大垂直位置非常接近。从表3的变形计算结果可知，沈珠江模型最大挠度为7.8cm，轴线向位移最大为1.1cm，最小为-1.1cm。Wolffersdorff模型最大挠度为11.3cm，轴线向位移最大为1.7cm，最小为-1.6cm。Wolffersdorff模型计算的最大扰度比沈珠江模型增加45%，相比下Wolffersdorff模型的计算结果偏于安全。

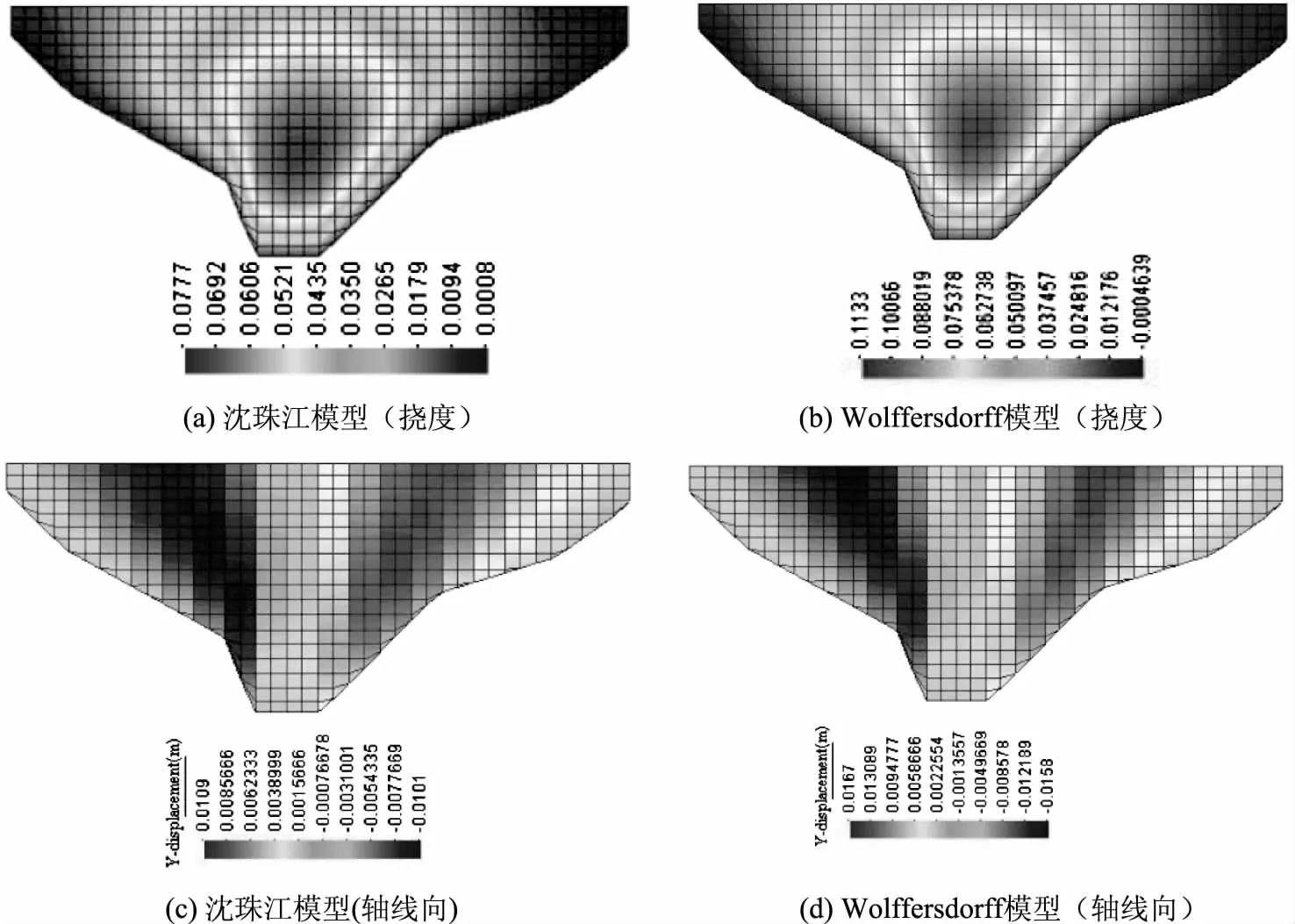
图8 蓄水期面板位移云图

如图9蓄水期面板应力云图所示，2种模型的顺坡向和轴线向的应力分布规律相似，都能够体现顺坡向应力中部受压，顶部和底部受拉的状态，轴线向应力中部受压，两边受拉状态，应力状态分布合理。沈珠江模型最大顺坡向应力为2.11MPa，最小为-0.22MPa，轴线向最大应力为1.1MPa，最小为-0.4MPa。Wolffersdorff模型最大顺坡向应力为5.06MPa,最小为-0.1MPa，轴线向最大应力为2.68MPa，最小为-0.4MPa。从计算结果可以看出，Wolffersdorff模型计算的面板应力分布比沈珠江模型更为合理。沈珠江模型计算的混凝土面板底部顺坡向拉应力存在应力过大的问题，与实际情况不符。

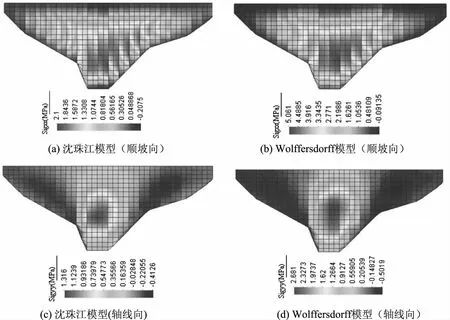
图9 蓄水期面板应力云图

4 结论

(1)Wolffersdorff模型的建立是以连续介质力学为基础，沈珠江模型是以弹塑性模型为基础，两者理论不同，但两模型通过对仙游面板堆石坝的坝体及面板应力应变计算对比分析，两者结果相差不大，从实际验证了改进后的Wolffersdorff模型可以应用于实际工程的应力应变分析。

(2)在混凝土面板应力应变计算方面，相比于沈珠江弹塑性模型，Wolffersdorff模型计算参数简单，容易确定，使用简便，且能够反映堆石料剪胀性，应力应变非线性等力学特征。但是该模型也存在一些不足，如不能考虑堆石料流变特征等，有待进一步研究。