北疆多厢互联式输水渡槽隔震问题研究

陈学光，李海枫

(1.新疆水利水电勘测设计研究院有限责任公司，新疆 乌鲁木齐 830000；2.中国水利水电科学研究院，北京 100038)

1 概述

我国是世界上地震最活跃的国家之一，目前国内很多区域、长距离调水工程基本穿越地震带，引调水工程的跨渠(沟)建筑物输水渡槽一旦遭受震害，将可能造成巨大损失[1]。因此，对于高烈度地区，设置何种隔震措施以削弱渡槽地震响应是一个非常值得研究的问题。目前，水工建筑物抗震设计标准规定对于VII度以上地区，宜采取减隔震设计，但是并未给出详细的减隔震设计流程[2- 3]；非线性时程分析方法虽然可以较精确地进行隔震计算分析，但是该方法难度较大且相对比较费时，不便于设计人员掌握。

本文将基于振型分解反应谱的等效线性化分析方法用于多厢互联式渡槽隔震设计；多厢互联式渡槽横槽向可视为考虑Housner一阶晃动的双自由度质量弹簧体系，顺槽向视为不考虑水体作用的单自由度质量弹簧体系，横槽向为设计控制方向，顺槽向为验算方向；等效刚度和等效阻尼比可由ASSTHO规范提供的等效线性化方法进行确定。该方法方可有效地进行多厢互联式渡槽隔震设计。

2 隔震简化模型及分析方法

2.1 隔震简化模型

对于常规梁式渡槽而言，可采用隔震简化模型进行研究。由于渡槽结构的特殊性，槽内有质量巨大的水体，顺槽和横槽方向上水体与槽体间相互作用是不同的。

鉴于空槽工况是顺槽向抗震最不利工况，建立顺槽向模型时可忽略水体的作用，参考规则桥梁结构隔震模型的形式，同时忽略槽墩刚度和阻尼影响，渡槽结构隔震模型可简化为仅有一跨槽体质量的单自由度模型，如图1所示。图中M为一跨槽体质量，kb和Cb分别为一跨槽体下所有隔震支座的纵向刚度之和以及阻尼系数之和。

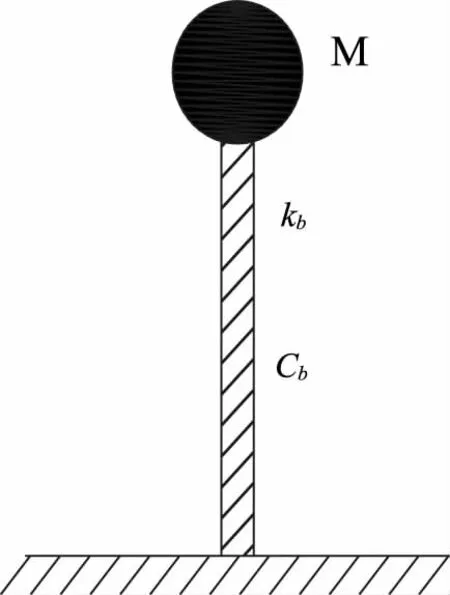
图1 单自由度模型

当地震激励方向为横槽向时，水体与槽体两侧壁之间存在复杂的动力相互作用，由GB 51247—2018《水工建筑物抗震设计标准》可知，渡槽隔震设计中采用Housner一阶水体晃动模型。根据聂丽英等关于多个梁式渡槽横槽向隔震简化模型对比研究可知[4]，槽墩对槽-水耦合体与隔震装置构成的结构体系影响较小，可以假定槽墩为刚体，即渡槽横槽向隔震模型可以采用双自由度模型。当槽墩刚度远大于支座刚度时，槽墩刚度、阻尼对整个结构体系的刚度、阻尼影响很小，故在进行隔震设计时可忽略槽墩的影响[11]。综合以上分析，渡槽横槽向隔震模型可以采用如图2所示的双自由度模型。图中，mc等效水体晃动质量(kg)；kc为等效水体晃动刚度(N/m)；cc为水体阻尼系数(N·s/m)；mb为等效固结水体与一跨槽体的总质量(kg)；kb为一跨槽体下所有隔震支座的横向刚度之和(N/m)；cb为一跨槽体之下所有隔震支座的阻尼系数之和，(N·s/m)。

图2 双自由度模型

对于双槽和多槽结构，由于水体晃动周期以及对流晃动质量和等效刚度为单槽控制，且隔震装置在地震作用下水平位移相同，因此多槽上部水体模型为并联模型。以三槽为例，存在以下关系。

(1)

2.2 隔震分析方法

隔震结构地震反应分析方法取决于所处设计阶段、场地类型、支座的力学特性、设计结构的复杂程度等因素，鉴于渡槽与桥梁具有结构相似性，可参考桥梁隔震计算分析方法。目前，国内外规范中关于桥梁隔震计算分析方法大致可分为单自由度反应谱法、多自由度反应谱法、动力时程法等。当采用多自由度反应谱法时，隔震支座可简化为线性分析模型，即采用等效刚度和等效阻尼比进行描述。由于隔震支座具有非线性特性，支座等效刚度和等效阻尼比在整个地震过程中不是常量，而是支座位移的函数，采用多自由度反应谱法时，计算分析过程应进行迭代求解。

等效线性化方法的概念最初由Jacobsen提出。弹塑性结构的等效线性化方法，是以线性等效刚度考虑弹塑性结构屈服后的刚度衰减，以等效黏滞阻尼考虑结构的弹塑性耗能，通过求解等效弹性体系的响应，从而近似获得原来非线性体系的响应[12]，如式(2)所示。

(2)

式中，ξeq—等效阻尼比；ωeq—等效振动频率,Hz。

对于隔震系统而言，原来非线性系统的力—位移骨架曲线可用非退化的双线性模型来表示，如图3所示。

图3 非退化双线性模型

图中，Fy—隔震装置的屈服力,N；xy—隔震装置的屈服位移,mm；xeq—等效线性化对应的位移,mm；xu—隔震装置所允许发生的最大位移,mm；K1—弹性刚度,N/m；K2—屈服后刚度,N/m；α=K2/K1—屈服后刚度比，一般取0.15。

等效线性化方法的关键在于确定等效刚度Keq和等效黏滞阻尼系数Ceq或等效阻尼比ξeq，其确定原则是等效线性系统要与原来非线性系统的位移反应或能量耗散的均方差达到最小。如果采取的等效原则不同，那么等效求得的等效刚度和等效阻尼比也不同，因此形成不同的等效线性化方法[10- 11]，具体见表1。根据已有研究成果如图4—5所示，桥梁设计规范中采用等效线性化方法为ASSTHO规范提供的等效线性化方法，鉴于渡槽与桥梁具有结构相似性，建议渡槽结构采用ASSTHO规范提供的等效线性化方法进行隔震设计。

图4 等效刚度比随延性比的变化曲线

图5 等效阻尼比随延性比的变化曲线

表1 等效刚度与阻尼比公式

3 隔震参数确定

隔震周期和隔震装置等效附加阻尼比这两项参数直接决定了隔震结构地震响应值的大小。要达到将结构与可能引起破坏的地面运动尽可能分离开来的隔震目的，可通过延长结构基本周期，避开地震能量集中范围，从而降低结构的地震力；通过延长周期以达到地震力折减，必然伴随着结构位移增大，带来设计上的困难。因此，对隔震周期选取不宜过大，在受力减小同时还应满足位移控制要求。输水渡槽设置有止水带，所以隔震同时也需要控制槽身在地震作用下位移的大小，确保不会因为位移过大而导致渡槽漏水，造成不必要的经济损失。张艳红等研究指出[12]，为了防止相邻渡槽之间的止水材料被拉断及地震过程中出现落梁现象，支座变形不宜超过0.075m，但相关规范并无规定，故位移限值需根据具体工程来具体确定。

根据聂丽英等人[13]研究，渡槽隔震周期Tb的确定原则可以总结为如图6所示：

图6 隔震周期选择示意图

(1)隔震周期Tb假定时需满足隔震前槽体振动周期T0的两倍，并小于水体晃动周期Tc，即式(3)所示。

2T0

(3)

式中，Tb—隔震周期,s；T0—隔震前振动周期,s；Tc—水体晃动周期,s。

(2)选取隔震周期后，进行隔震设计，得到隔震设计参数，随后对θ值进行验算，确保θ值大于或等于0.9，以避免隔震设计对于波高的放大影响。

(4)

式中，θ—等效晃动频率与水体晃动频率之比；γ—质量比；η—刚度比。

渡槽在加入铅芯橡胶隔震支座后，渡槽阻尼体系仍然可以采用经典阻尼假定[14]。从隔震原理来说，隔震设计会导致结构在地震作用下位移增大，而阻尼的增加可以在限制位移的同时减小结构的受力。现有隔震设计中附加阻尼的方式通常有2种，一是通过隔震支座自身提供，如铅芯橡胶支座、高阻尼橡胶支座等；二是通过附加阻尼装置提供，如非线性液体黏滞阻尼器。对于渡槽隔震而言，比较常用的铅芯橡胶支座，国内外众多学者经过试验研究，发现其等效附加阻尼比在0.1～0.3之间。而众多公司生产的铅芯橡胶支座的产品说明书中也可以看出，常规的LRB支座的等效附加阻尼比在0.1～0.3之间。故在进行铅芯橡胶支座隔震设计时，可在0.1～0.3内假定其等效附加阻尼比。目前，附加阻尼比为0.15的支座最为常见。

4 隔震设计流程

对于常规梁式渡槽而言，可采用基于反应谱的等效线性化分析方法进行隔震设计[18]。由第2节隔震简化模型可知，横槽向为考虑Housner一阶晃动的双自由度质量弹簧体系，而顺槽向为不考虑水体作用的单自由度质量弹簧体系，横槽向为设计控制方向，顺槽向为验算方向。虽然目前工程采用的隔震装置有所不同，但是隔震设计基本流程是一致的，具体如下。

(1)根据第3节提及的隔震周期选择准则，选择隔震周期，并计算其等效刚度；

(2)假定隔震装置的附加等效阻尼比，修正反应谱并计算地震响应；

(3)验算剪力和位移是否满足抗震要求，若不满足，则重新选择隔震周期；若满足，则采用等效线性化方法进行隔震装置的参数计算；

(4)完成隔震装置参数计算后，需验算隔震周期是否满足第3节中对于θ值的限定，若不满足，则重新假定隔震周期进行隔震计算即重复第(1)～(3)步；

(5)进行顺槽向抗震验算，若不满足要求，则需重新假定隔震周期进行隔震计算即重复第(1)～(4)步。

(6)确定隔震支座几何尺寸，并校核支座性能(承载力、稳定性和构造要求等)。

5 多厢互联式渡槽隔震措施研究

5.1 工程概述

北疆某输水渡槽区域位于地震烈度为Ⅷ度为同，槽身总长54m，双槽3跨箱形结构。槽身采用C50纤维钢筋混凝土，单向预应力简支梁结构，跨度为18m；各跨布置2孔箱形槽身，槽身净宽为4.4m，槽身净高度7m，总高度7.5m。计算模型如图7所示，其中槽身和槽墩采用六面体实体单元模拟，支座采用弹簧单元模拟，锚索采用三维锚索单元，冲击动水压力采用附加质量单元模拟，对流动水压力采用附加质量单元+弹簧单元组成的弹簧系统来考虑。根据规范规定，采用振型分解反应谱法开展渡槽动力分析；该渡槽属于梁式渡槽，可采用基于振型分解反应谱的等效线性化分析方法进行隔震支座设计研究，并采用振型分解反应谱法进行不同支座型式下渡槽隔震效果评估。

图7 槽身及槽墩有限元模型

5.2 地震工况下槽身应力分析

由渡槽应力云图可知(如图8所示)，地震工况下边墙、中墙中下部以及顶板中部区域环向受拉，拉应力基本在1.2MPa以内，仅在边跨靠近边墩附近的中墙底部(即距八字墙顶部0.8m区域内，深度约8cm)的环向拉应力超过了1.85MPa，最大可达3.0MPa；内壁纵向槽身各跨连接处存在很小的受拉区，拉应力基本在0.4MPa以内，其他区域受压；内壁第一主应力全部为拉应力，大部分区域拉应力在1.50MPa以内，中墙底部主拉应力超过2.24MPa，甚至达到3.0MPa。槽身外壁环向边墙上部以及底板大部分区域受拉，拉应力基本在1.50MPa以内，其中，底板端部部分区域拉应力超过1.85MPa，最大可达2.50MPa；槽身各跨连接处纵向存在一定范围受拉区，最大拉应力不超过1.0MPa，其他区域均受压；外壁第一主应力基本在2.20MPa以内。综合来看，地震工况下内壁环向仅在边跨部分剖面存在很小范围的超标拉应力(即拉应力大于1.85MPa)，纵向不存在超标拉应力，这使得槽身基本满足“裂缝控制等级二级”的要求。

图8 地震工况时内壁应力分布云图(单位：0.01MPa)

5.3 隔震支座设计研究

对该渡槽而言，其设防地震目标地震加速度为0.15g。单跨槽体体重9.135×105kg，槽体水重9.07344×105kg。隔震支座应布置在墩顶与槽身之间，每个槽墩顶部布置6个支座，支座等效阻尼比取0.15。工程场地特征周期为0.30s，隔震前渡槽基本周期T0为0.396s，水体晃动周期Tc为3.399s，隔震前支座处最大剪力Q未隔震为7371.064kN。晃动控制周期Tc=3.368s，由式(3)可知，该渡槽隔震周期Tb应满足：0786s≤Tb<3399s。根据本工程特点，在隔震前周期基础上放大2～6倍T0来研究隔震支座选取问题，具体计算成果见表2。

表2 铅芯橡胶隔震支座设计参数

由于渡槽是输水建筑物，设置有止水带，所以隔震同时需控制槽身在地震作用下位移大小，确保不会因为位移过大二导致渡槽漏水，造成不必要的经济损失。为防止相邻渡槽之间的止水材料被拉断及地震过程中出现落梁现象，支座变形不易超过0.075m。参考类似工程经验并结合本工程特点，选取4倍隔震周期进行隔震支座设计。

因此，每个槽墩支座特征参数为：

Qd=155.64×103N；K1=72.00×106N/m；K2=10.80×106N/m。

对于单跨而言，每侧设置3个支座，每个隔震支座的特征参数为：

Qd=51.88×103N；K1=24.00×106N/m；K2=3.6×106N/m；等效阻尼比0.15。

5.4 隔震效果评估

为评估隔震效果，现将刚性支承、抗震型盆式支座以及铅芯橡胶支座3种支座形式下的渡槽动力工作性态进行对比分析。表3为3种不同支座型式下通水时支座最大位移对比情况，图9—10为3种不同支座型式下通水时槽身内壁环向及纵向正应力分布对比情况。

表3 支座位移对比表 单位：mm

图9 不同支座形式下渡槽内壁环向应力分布对比图

图10 不同支座形式下渡槽内壁纵向应力分布对比图

由于采用铅芯橡胶支座，降低支座水平刚度，改变渡槽结构的振动特性，减少槽身地震反应，减低了槽墩的地震反应；此时，支座处的最大顺槽向位移为36.20mm，最大横槽向位移为35.57mm，满足支座变形不易超过75mm的要求。由槽身内壁应力分布云图可知，由于采用铅芯橡胶支座等隔震措施，减少槽身的地震反应，相比刚性支座和抗震型盆式支座，槽身内外壁应力大幅度降低，基本不存在应力超标区。

综合以上分析可知，采用铅芯橡胶支座以后，改变渡槽结构的振动特性，减少槽身地震反应，相比其他两种支承型式，槽身内外壁基本不存在应力超标区，虽然支座处位移有所增大，但最大支座变形不超过75mm，满足相应变形要求。

6 结论

通过以上研究，可得出如下研究结论：

采用基于振型分解反应谱的等效线性化分析方法用于渡槽隔震设计可以真实反映输水渡槽的应力应变情况。通过铅芯支座的缓冲作用，改善了槽身应力分布情况，避免地震时槽身产生较大剪力导致失稳。采用铅芯橡胶支座以后，可明显改善槽身振动特性，减少槽身地震反应，槽身内外壁基本不存在应力超标区，但最大支座变形不超过75mm，满足相应变形要求，隔震效果显著。为高地震区输水渡槽的隔震设计提供他宝贵的工程经验。