基于TOPSIS模型及综合权重的武威市水资源承载力和水安全评价

黄 博，李博文，雷正烨，康元丽，马亚丽，孙栋元，李 龙

(甘肃农业大学水利水电工程学院，甘肃 兰州 730070)

水资源是国家可持续发展的重要战略资源，也是生态环境建设的基础资源[1]。水的资源属性本质上是水为人类社会存续提供生活生产资料与服务功能的能力[2]，它已经成为制约人类生存和发展的关键因素[3]。长期以来，武威市自然环境恶劣，加之人口的增长和社会经济的发展，水资源量低于严重缺水线[4]。水资源匮乏，生态环境脆弱，供需矛盾突出，这些因素成为了制约城市发展和社会经济发展的主要因素。

科学评价水资源承载[5]和水资源安全是保障社会经济稳定发展的前提。水资源安全研究是水资源安全战略的基础，是国内外研究的热点[6]。目前，许有鹏[7]建立模糊综合评判方法评价区域水资源承载力，门宝辉等[8]基于云理论评价北京市水资源承载力，相关研究较多，这里不再赘述。刘晓等[9]提出水资源承载力的新定义及相关的量化方法；针对水资源安全概念，笔者认为水资源安全是国家或地区水资源在可持续发展的目标下，支撑水资源总量、水资源质量和水资源应急保障等方面的水平。吴开亚等[10]选取万元工业产值耗水量、水资源开发利用率等指标建立评价指标模型，对巢湖流域水资源安全进行评价；还有一些学者认为，水贫困指数[11]是水资源安全评价的重要指标。水资源承载力和水资源安全的综合研究成果相对较少，研究方法主要有经验估算法、指标体系评价法等，田海兰等[12]用经验估算-供需平衡法对河北省海域承载力进行研究，从精度方面来看，不能满足要求；指标体系评价法是目前国内进行水资源承载力和水资源安全研究运用最广使用最多的方法，操作上直观、简便，结果更加可信。王涛等[13]建立模糊分析模型，利用层次分析法对安庆市水资源承载力进行研究；张志君等[14]建立模糊集对分析法对新疆水资源安全进行研究；程芳芳[15]利用主成分分析法对太原市水资源承载力进行研究。

基于上述研究背景，本项目以武威市水资源承载和水资源安全立项。采用水资源承载力TOPSIS模型和水资源安全评价指数，利用综合权重[16]确定指标的评价思路，分别从主、客观两方面考虑，保留经验打分优势的同时保证估计精度，提高结果的可信度。研究结果主要分析水资源承载能力和水资源安全等级及其成因，为未来武威市水资源综合开发利用提供决策依据，同时为我国其他干旱半干旱地区水资源承载和水资源安全评价提供借鉴。

1 研究区概况及数据来源

1.1 研究区概况

武威是甘肃省辖地级市，位于河西走廊东端。南北长326km，东西宽204km，总面积3.23万km2。武威地势呈西高东低，属温带大陆性干旱气候。多年平均水资源总量14.94亿m2，人均水资源量819m2。年平均日照时数2876.9h，年平均蒸发量2163.6mm，年平均降水量212.2mm。武威市水资源水平较低，供不应求。

1.2 数据来源

武威市2011—2020年水资源承载力评价指标值原始数据来源于《甘肃省水资源公报(2011—2020)》《中国统计年鉴》等。

2 研究方法

2.1 评价指标体系的建立

水资源评价指标体系是一个面积范围大和跨领域的复杂系统[17]，本文结合武威市水资源现状，主要参考高玉琴等[18]、李明然[19]关于水资源评价体系的指标选取，以科学性、综合性和可获取性原则为基础，结合国内外学者现有的研究成果，分别从水资源系统、社会系统、经济系统和生态系统中选取了24项评价指标，构建了武威市水资源评价指标体系，见表1。

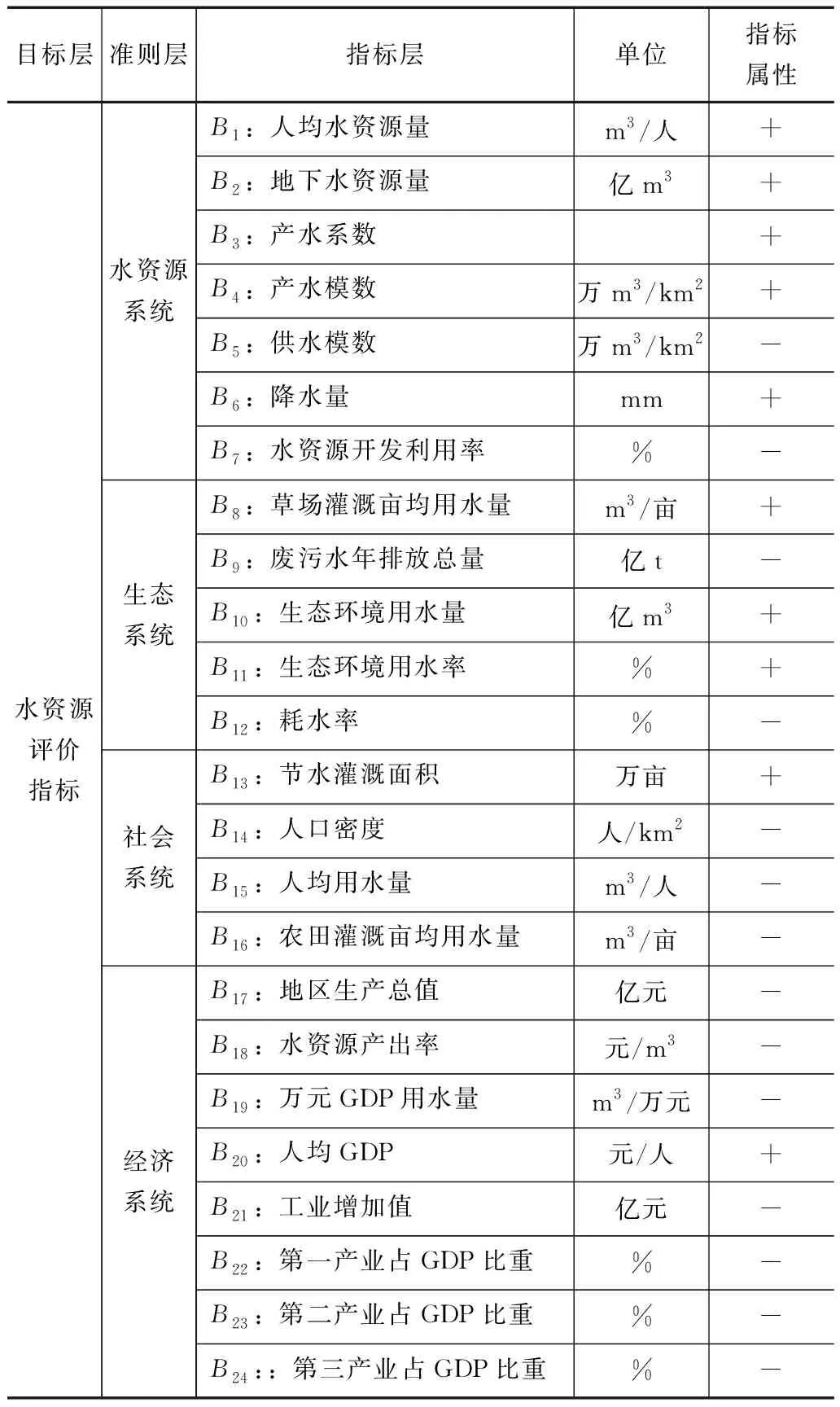
表1 武威市水资源评价指标体系

2.2 主观权重

层次分析法是一种简便、灵活而又实用的多准则决策方法[20]。是用群体判断克服单一判断的主观偏好进行群体综合，并通过判断矩阵的一致性检验检查主观判断的一致性，最后再以定量的形式给出排序结果[21]。

(1)构造判断矩阵。利用对比法和1～9尺度表[22]。

主观评价矩阵U，uij表示因素ui对uj的相对重要性数值(i，j=1，2，…，n)，取值范围为1～9，uji=1/uij

(2)计算重要性排序。根据判断矩阵，由公式

UW=λmaxw

(1)

(3)一致性检验

CI=(λmax-n)/(n-1)

(2)

CR=CI/RI

(3)

其中RI是对应指数标度的随机一致性比率，当CR<0.1时，满足一致性检验。

2.3 客观权重

2.3.1熵权法

熵权法基于信息论，是一种通过各指标信息效用值的大小来确定指标权重，着重突出指标间局部差异的客观赋权的方法，可以避免由于人为主观因素造成的偏差[23]。

(1)建立数据矩阵：A=(xij)m×n，其中xij为第i年第j个指标的数值。

(2)数据标准化处理：对水资源承载力指标进行标准化处理，目的是为了消除各项指标的计量单位不同带来的影响。

对原始数据进行标准化处理得到标准化矩阵A′。

a.对正向指标：

(4)

b.对负向指标：

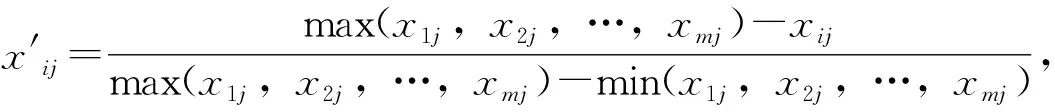
(5)

(3)计算第j项指标的熵值：

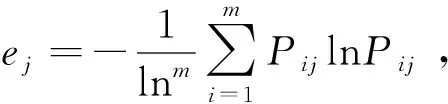
(6)

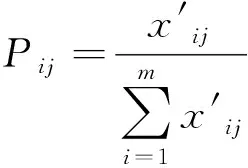
(4)计算各项指标的权重：

(7)

2.3.2CRITIC权重法

CRITIC权重法是根据评价指标的对比强度和冲突性来综合衡量指标的客观赋权法[24]。对于多指标多对象的综合评价问题，CRITIC权重法去消除一些相关性较强的指标的影响，减少指标之间信息上的重叠，更有利于得到可信的评价结果[25]。

(1)计算标准差：

(8)

(2)计算信息量：

(9)

式中，rij为指标间的相关系数。

(3)第j个指标的权重：

(10)

2.4 综合权重

综合权重可对主客观权重进行协调优化，对多指标综合评价问题确定其综合权重[16，26]。乘数合成归一法能够有效反映出各项指标在评价体系中的权重占比，这样得到综合权重性能更高，使结果更具有参考性。其最优赋权法计算公式为

(11)

2.5 TOPSIS模型和安全评价指数

2.5.1TOPSIS模型

TOPSIS法又称优劣解距离法，是根据评价对象与理想解的欧氏距离对评价对象进行排序。通过分析样本的优劣状态，建立正(负)理想点，确定样本与理想点的距离，进而求得样本与理想点的贴近度[27，28]。具体步骤如下。

(1)将负向指标进行正向化处理，得到决策矩阵Z=(zij)m×n，

(12)

(13)

(3)计算各评价对象指标值与最优解、最劣解的距离：

(14)

(4)确定贴进度Si;

(15)

Si越大，水资源承载力就越大。参考孙维维[29]在安徽省水资源承载力评价研究中水资源承载力等级划分，见表2。

2.5.2安全评价指数

利用线性加权法计算水资源安全评价指数Ci，公式为：

表2 承载力评价等级

(16)

式中，wj—第j个指标的综合权重值；xij—其标准化值。根据水资源安全评价指数的大小，采用均分原理，对安全评价等级进行划分[30]，见表3。

表3 安全评价等级

3 结果与分析

3.1 原始数据分析

经整理得到武威市水资源评价指标原始数据，见表4。

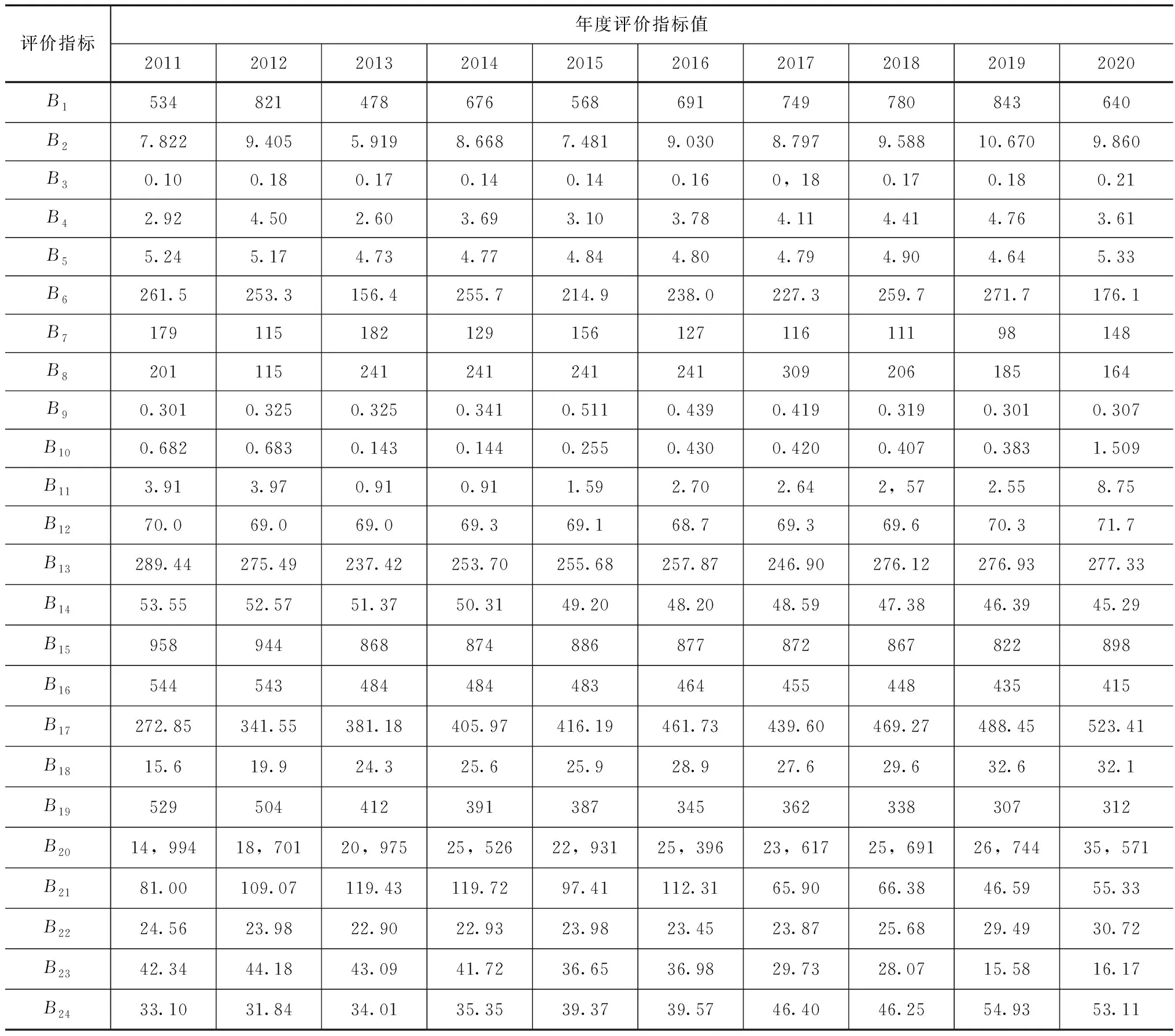
表4 武威市2011—2020年水资源评价指标原始数据

根据表1可知，武威市2011—2020年人均水资源量在甘肃省水资源量平均线1100m3/人以下，水资源警戒线700m3/人处徘徊，处于变化的不稳定状态。地下水资源量变化不大，处于稳定状态。降水量受气候条件影响较大，年降水量在150～270mm之间浮动，低于甘肃省年降水量平均水平。水资源开发利用率远超国际公认的40%的水资源开发生态警戒线，严重挤占生态流量，水资源自净能力锐减。废污水年排放总量先增大后减小，10年内基本维持在0.3亿t左右，总体呈逐年稳定下降趋势，有利于生态系统发展。耗水率稳定维持在70%左右，相较于全国的50%和甘肃的62.3%来说耗水率较高，不利于生态系统发展。节水灌溉面积呈缓慢减少趋势，水资源利用程度并未得到有效发展。万元GDP用水量呈下降趋势，水资源与经济的协调度稳步提高。地区生产总值、人均GDP呈逐年快速增长状态，2020年地区生产总值相较于2011年翻了一番左右，2020年人均GDP是2011年的2.3倍左右，经济发展态势良好。第一产业占GDP比重稳定增大，第二产业占GDP比重稳定减小，第三产业占GDP比重稳定增高，产业发展的重心正由工业逐渐向农业和手工业转变。

3.2 指标权重

3.2.1一致性检验

层次分析法的计算结果显示，最大特征根为27.5756，根据RI表查到对应的RI值为1.6497，因此CR=CI/RI=0.0942<0.1，通过一次性检验，见表5。

表5 一致性检验结果

3.2.2基于主、客观方法的综合权重

利用层次分析法计算指标的主观权重，利用熵权法和CRITIC法计算指标的客观权重。为了数据更具有参考性，增加数据可信度，对3种不同的方法采用综合权重法，利用公式(11)求出综合权重，见表6。

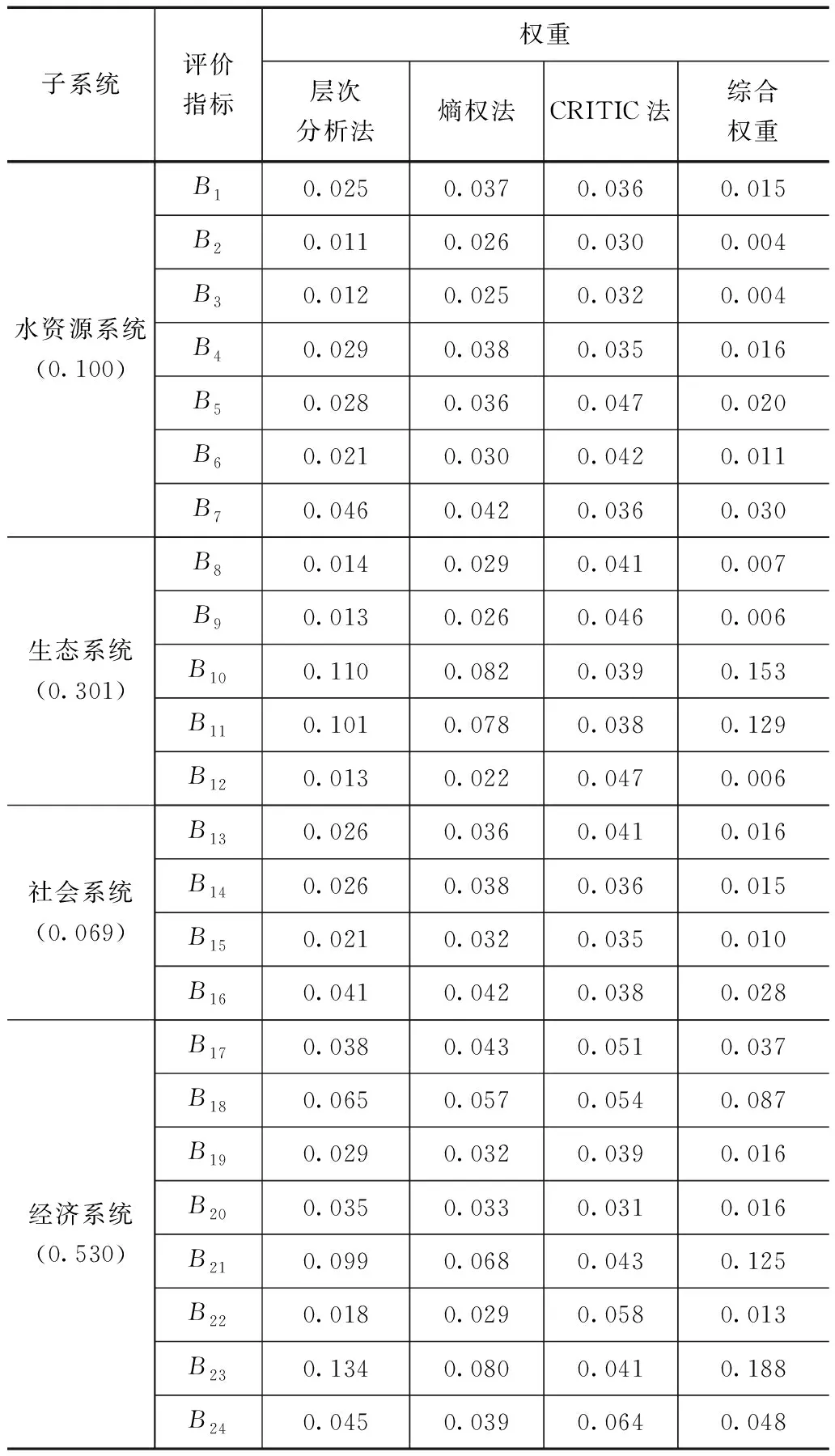
表6 水资源评价指标权重

如图1所示，总体来看经济系统(0.530)和生态系统(0.301)各项指标所占权重较大，对水资源承载力的影响突出，水资源系统(0.100)和社会系统(0.069)各项指标所占权重较小，对水资源承载力的影响较小。生态系统中5个指标：生态环境用水量(0.153)和生态环境用水率(0.129)的综合权重都在0.1以上，说明生态环境用水量和生态环境用水率对水资源承载及安全有较大影响，加大生态环境用水量和提高生态环境用水率可以提高武威市水资源承载能力和水资源安全等级。经济系统中个指标：工业增加值(0.125)、第二产业占GDP比重(0.188)的综合权重都在0.1以上，说明第二产业对水资源承载及安全的影响较大，保障产业链、供应链稳定，现仍需要高质量发展第二产业，但是第二产业高能耗、高排放、低能效问题突出[31]，在发展第二产业的同时，水污染、污水排放任务紧迫而艰巨。

图1 4种权重比较

3.3 水资源承载力贴近度Si评价分析

根据公式(15)，利用TOPSIS模型对武威市2011—2020年水资源承载力进行评价，得到年度评价值、评价等级及排序，见表7。

表7 贴近度Si计算结果、评价等级及排序

结合表7来看，近10年武威市水资源承载力贴近度Si平均值为0.10，水资源承载力水平较低。2014年贴近度Si为0.046，该年水资源承载力水平最低，2020年为0.230，该年水资源承载力水平最高。2011—2014年小幅度降低，2014—2020年逐年稳步上升，2020年水平为近10年最好，水资源承载力等级达到超载等级，其余年份承载力水平基本保持在0.1附近，均处于严重超载等级。

3.4 水资源安全评价值Ci分析

根据公式(16)，利用水资源安全评价指数对武威市2011—2020年水资源安全进行评价，得到年度评价值、评价等级及排序，见表8。

表8 安全评价值Ci计算结果、评价等级及排序

结合表8分析，10年间武威市水资源安全评价值Ci平均值为0.41，发展较为稳定。2013年水资源安全评价值Ci为0.200，水平较差，其余年份处于临界安全和较安全状态。2020年水资源安全评价值Ci为0.717，水平较好，较2013年的最低值0.200高出了接近50个百分点，达到了较安全水平。

3.5 变化趋势对比分析

根据TOPSIS模型计算得出水资源承载力评价值，如图2所示，武威市2011—2020年水资源承载力贴近度Si线性拟合值整体呈缓慢上升趋势；由水资源安全评价等级指数得出安全评价值，可以看出武威市2011—2020年水资源安全评价值整体呈上升趋势。

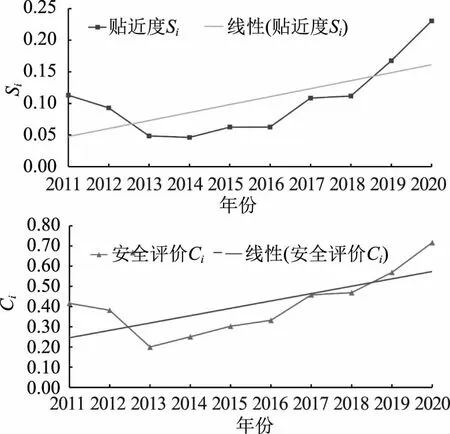
图2 承载力贴近度Si与安全评价值Ci变化趋势

TOPSIS模型与水资源安全评价值最小值年份出现些许差异，是由于TOPSIS法在判断贴近度时需要计算评价指标与最优解、最劣解的距离，可能会出现与最优解距离小与最劣解距离也小的问题，因此数据表现出差异性，属于随机误差[32]。2013、2014年水资源评价指数皆处于10年期间的较低水平，2013年水资源承载力为0.049水资源安全评价指数为0.200，2014年水资源承载力为0.046水资源安全评价指数0.251，说明2013和2014年武威市水资源承载和安全都非常脆弱。究其原因，2013年武威市生态环境用水率极低，仅有0.91%，与10年平均水平3.05%相比相差3倍，；且人均水资源量处于10年期间的最低值，首次突破小于500m3/人，严重制约了水资源承载力，导致水资源安全处于极不安全水平。就客观来讲，受到了干旱气候的影响，2013年武威市平均降水总量为176.1mm，较历年同期减少了三成，出现了严重的冬、春、夏、秋连旱，持续干旱对农业牧业生产和生态环境造成了严重的影响。2020年水资源承载力较好，主要是客观因素如降水量、总水资源量达到近10年最大值，其次人均GDP明显提升，万元GDP用水量呈逐年下降趋势，加之经济快速发展，促进了武威市的良好发展，为未来水资源承载力和水资源安全持续向好发展奠定基础。

4 结论

(1)利用主观和客观两方面确定综合权重确定评价指标权重可以提高指标的参考性，文章评价结果与武威市水资源开发利用情况相符，有很强的参考性；在水资源评价中，经济系统和生态系统所占权重较大，水资源系统和社会系统所占权重较小。

(2)生态系统对水资源承载和水资源安全评价的影响很大，生态环境用水量和生态环境用水率对武威市水资源承载力和水资源安全有较大影响。未来应加大生态环境用水量同时保证生态环境用水效率，完善现代化农业生产技术，提高水资源利用率。

(3)武威市水资源承载力水平最好的年份为2020年，最差的年份为2013年。水资源承载力处于严重超载等级；武威市水资源安全水平最好的年份为2020年，最差的年份为2014年。水资源安全处于临界安全等级。未来武威市水资源承载力和水资源安全均有向好发展趋势。

(4)水资源承载力是水资源安全的基本度量，采用同一评价体系对武威市水资源承载力与水资源安全进行评价，评价的结果一致，可以相互验证。

通过此次研究，对武威市2011—2020年10年间水资源承载力和水资源安全有了简单认识，水是各项可持续发展目标的基石。该地区水资源问题还面临着巨大挑战，解决地区水资源承载力和水资源安全问题，要深刻理解经济与生态之间的平衡关系。此外，文章仍有不足之处，水资源安全目前还没有一个准确的定义，在评价水资源安全时，相关概念、理论、评价体系的建立和评价方法还需要进一步研究。