基于数值模拟的雾炮风筒结构优化

王文丽,毕方淇,张立凯,宫玉敏,张义胜

(淄博市农业机械研究所，山东 淄博 255038)

近年来，在农业远距离植保、城市建筑及特种作业场地降尘、养殖区域降温等领域，雾炮机的使用日趋广泛[1-2]。对于雾炮领域的研究主要集中在喷嘴雾化方面，史永杰[3]针对目前存在需大功率设备进行加压、雾化范围小及液滴分布不均匀等问题,研究了液滴粒径离散程度，发现喷腔长孔比及出口收缩角、喷嘴出口直径对喷嘴液滴粒径的影响显著。刘涛[4]对气液分散体系中两液滴相互碰撞过程进行研究，部分揭示了气液流动中液滴碰撞的物理本质。陈云等[5]对雾炮管路系统进行设计分析，有效降低了雾炮机运行过程中的噪声。周红伟等[6]通过加大管路通径、优化管路连接方式，提高了雾炮机喷雾效果。

雾炮机工作中，液体首先依靠喷嘴雾化，随后通过风力进行输送，雾化与风送相互配合才能符合既定的要求并取得良好的效果，而风送气流也在较大程度上影响了雾炮机的最大喷射距离。当下对于风送和风筒结构研究较少，尚未查到关于风筒结构对气流流动的影响研究。本文针对风筒锥角、锥角起始位置及内部导风板倾斜角度三因素，采用正交试验的方法，通过对不同结构风筒进行数值模拟，以期得出较优的风筒结构，在不改变设计功率的前提下，提高气流在风筒外流速，进而提高送风效率。

1 模型与试验设计

1.1 几何模型

本文所研究的雾炮机风筒内径为325 mm，内部扇叶采用铝制7叶风扇，扇叶实物如图1(a)所示。其中，扇叶中心区域直径105 mm，厚度40 mm，叶片长度95 mm，叶片宽度56 mm，厚4 mm。对轴孔进行简化，几何模型如图1(b)所示。

(a)扇叶实物 (b)模型

为减少计算量，采用周期性几何模型进行流域建模，并选择整圆周的1/7进行建模，如图2所示。

图2中，1为流体计算中的稳流区域，位于风筒入风口外，直径320 mm，长200 mm。2至3为风筒区域，总长500 mm，其中，2为风筒内扇叶所在周期性旋转区域，长60 mm；3为风筒内扇叶外部分，长440 mm，区域3由圆柱段和圆锥段组成，靠近区域2部分为圆柱段，靠近区域4部分为圆锥段，具体尺寸见表1。4为外流域，直径1 200 mm，长3 600 mm。5为导风板，长180 mm，高60 mm，与风筒出风口间距为10 mm，紧贴在风筒内壁上，其倾斜角度见表1。

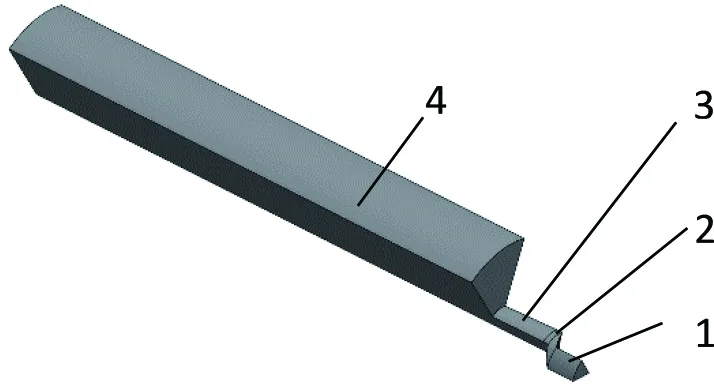
(a)整体模型

1.2 试验设计

雾炮机风筒结构较为单一，对内部气流造成影响的6个参数分别为：风筒长度、风筒直径、风筒是否带有锥角及锥角部分长度、风筒内是否存在导流板和风机安装位置。综合考虑整机尺寸协调性和结构强度，确定风筒长度、风筒直径和风机安装位置3个参数保持不变，对剩余参数进行研究。取风筒锥角A、锥角起始位置与进风口距离B，导风板倾斜角度C为设计因子，其中：锥角A取值不宜超过10°，否则易导致出风口直径过小，阻碍气流流出，为较好覆盖整个区间和兼顾区间边界值，取2°、5°、8°三值；根据市面风筒结构，考虑为进风口处电机安装预留空间，锥角起始位置与进风口距离B不可过小，B取100、200、300 mm；导风板倾斜角度C取值主要考虑让导流板起到导向作用，使流体能沿风筒方向前进更远的距离，取值不应过大，结合常见导流板角度，取0°、15°、30°。综上，建立三因素三水平正交表(见表1)，评价指标为外流域出风口壁面中心点风速vmax。

2 控制方程

对于流场分析，作如下假设：

1)工作介质为不可压缩连续流体；

2)流场计算收敛后处于稳定状态，流场物理量只与空间欧拉坐标有关而与时间无关。

流场按纳维-斯托克斯方程(N-S方程)[7]和连续性基本微分方程共同计算。纳维-斯托克斯方程( N-S方程)为

(1)

其中拉普拉斯算子

(2)

式中：X、Y、Z分别为3个坐标方向的质量力，N；μ为速度，m/s;ρ为空气密度，取1.225 kg/m3；p为压强，取101 325 Pa；v为空气运动学粘性系数，取1.8×10-5m2/s。

3 数值模拟

3.1 网格处理

根据建立的几何模型，综合考虑计算精度及计算经济性，确定采用混合网格对网格进行周期性设置，周期角度为51.428 57°。其中，扇叶所在区域2采用非结构网格，其与其他区域交界面Surface预设为interface，网格尺寸6 mm；其他区域采用结构网格，最小尺寸6 mm，增长率1.05，最大尺寸20 mm，结构网格整体Determinant质量0.6以上。网格划分如图3所示。

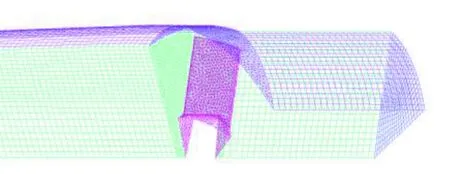
图3 网格划分

3.2 网格独立性验证

数值模拟中，网格数量对模拟精度和收敛性有重要影响，为保证计算可靠性，对网格进行独立性验证。分别采用235 784、466 887、964 572三种不同数量网格模型进行数值模拟，在相同边界条件下，流域出口壁面中心点风速vmax如图4所示。

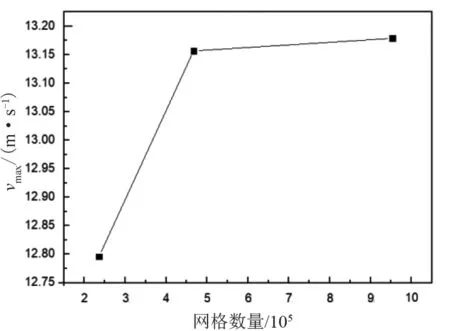
图4 不同网格数量下外流域出风口壁面中心点风速曲线

由图4可知，当网格数量较少时，模型计算误差较大；随着网格数量的增多，结果逐渐稳定。为在保证计算可靠性的前提下提高计算效率，采用466 887网格进行数值模拟。

3.3 边界条件及求解设置

网格导入FLUENT后，周期性边界自动识别为Periodic。旋流模型采用SSTk-ω[7-9]模型，风筒稳流区域侧单面壁为入口，入口为压力入口，压力为0。风筒之外所有区域均为出口，出口为压力出口，出口压力为0；扇叶区域采用MRF方式进行设置，转速1 500 r/min;扇叶壁面设置为滑移壁面，滑移方式为转动，与相邻区域相对转动速度为0。匹配扇叶两侧Interface。

为提高收敛速度，压力速度耦合采用Coupled算法[8-11]进行稳态计算。

4 结果及分析

经计算发现，模型最大速度发生在扇叶尖端区域，最大速度约25.1 m/s，流域整体流线图如图5所示。

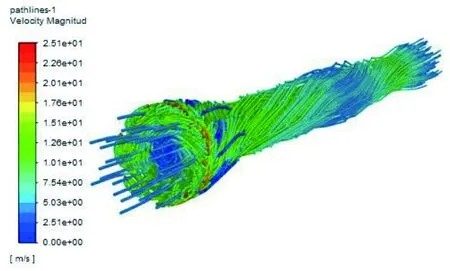
图5 流域整体流线图

根据图5可以看到，气流在经过风扇后，以一定螺旋角度向前流动，当气流离开风筒后，气流的螺旋前进会保持小段距离，最终逐渐趋于层流。

在模型外流域轴心处设置一条线，纪录计算收敛后不同位置的速度，绘制出速度-位置曲线如图6所示，汇总正交试验方案及结果见表2。

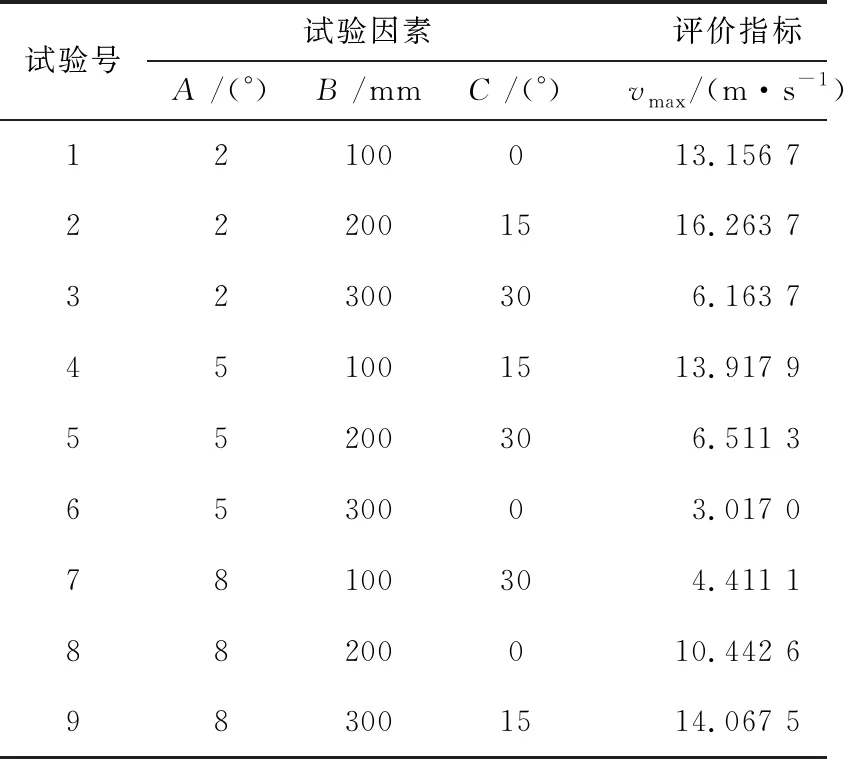
表2 正交试验方案及结果

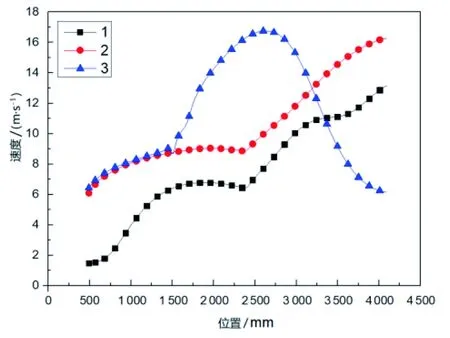
(a)试验1、2、3

由图6可以看出，当气流在离开风筒之后，中心轴线空气流动速度并不是立即衰减，会存在上升阶段。当风筒结构设计较为合理时，该上升阶段可持续较长时间，如试验1、2、8，即使距离出风口3 600 mm远时，其轴心速度依然有上升趋势；次之为工况4、9，气流到达该位置时，其速度已经开始衰减；结构较为不合理的工况为3、5、6、7，气流在离开风筒后衰减较快。由此可以看出合理的风筒设计对于保持气流速度的重要性。

根据表2可知，不同的风筒结构，吹出的气流流速差异较大。其中A1B2C2效果最好，外流域出风口壁面中心点风速vmax为16.263 7 m/s，为本次正交试验最优解。

对正交表进一步分析，计算其水平效应估计值I、K值和极差R,结果见表3。根据表3可知，对于影响气流在离开风筒后流动速度的重要程度，导风板倾斜角度>锥角>锥角起始位置与进风口距离。为此，推测产生这种现象的原因在于，当扇叶在风筒内转动时，带动气流以一定螺旋角度旋转，同时在风筒内形成一个个小的气旋，推动气流向前流动。当导风板处于一个合适的角度时，可以在较少阻碍气流流动的前提下，引导气流吹向指定区域；而当其设计不够合理时，效果将大打折扣。同时，通过试验数据可以看出，风筒锥角及锥角起始位置对送风速度同样存在影响，但相对来说，其影响程度低于导流板倾角造成的影响。为此，在后续优化设置时，可以首先固定其他参数，优先对导流板进行进一步的优化分析，之后再优化其他因素，预期可得到较为理想的效果。

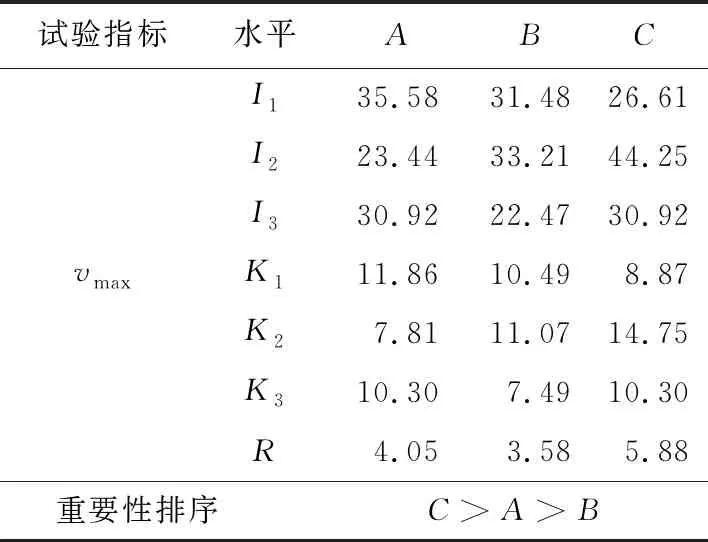
表3 最大轴心速度极差分析

5 结论

本文通过对雾炮机风筒建模并进行基于正交试验设计的数值模拟，得出如下结论：

1)根据基于正交试验设计的数值模拟，获得了外流域出风口壁面中心点最大风速16.263 7 m/s，得出最优风筒结构参数A1B2C2。

2)通过正交试验可知，导风板倾斜角度、锥角、锥角起始位置与进风口距离对外流域出风口壁面中心点风速大小影响程度是递减的，该研究可为后续风筒结构优化提供参考。