振动台正弦振动虚拟仿真技术研究

饶玉文，牛金皓

（1.南京晨光集团有限责任公司，南京 210000； 2.南京晨光集团有限责任公司，南京 210000）

引言

振动台作为模拟振动环境，检验产品可靠性、动强度的一种有效手段，已经被广泛应用于设计的验证试验中[1]。然而振动台在实际应用中受到试验设备和测点数量的限制不能全面获得试验件各个部分的响应特性[2]，因此在有些情况下不能仅仅以振动台试验结果作为结构、产品设计的唯一依据。虚拟振动仿真技术利用计算机技术的优势弥补了振动试验存在的缺陷，通过虚拟仿真不仅可以预示振动响应，还可以对产品试验不便测试的部位进行模拟测试[3]，指导试验开展和结构与方案设计。

电动振动台主要由活动系统（驱动线圈和工作台）、磁路系统、弹性支撑系统、导向系统及冷却装置等组成，其中导向机构限制振动台的横向运动，弹性支撑系统产生恢复力和支撑力[4]，活动系统是指在带有工作台面的骨架上绕制激励线圈，并用环氧树脂将两者固封在一起的组合件，通常称为动圈，动圈是活动系统的关键部件，是振动台的核心部分[5]。振动试验仿真最关键的技术是建立正确的系统分析模型[6]，因此可以获取准确的动圈模型后，施加对应真实状态下的边界条件和激振力便可模拟振动台的虚拟振动仿真。

本文以8 t电动振动台为对象，通过模态试验对动圈实物模型进行修正，利用ANSYS软件进行两次频响计算，最终求出正弦振动条件下台面两点平均控制的响应。

1 振动台结构模型建立

1.1 动圈结构建模

动圈是主要由骨架、线圈、工作台面和台面螺钉等部分组成，其中骨架部分含侧板和8片环形立板，结构示意图如图1所示。其中螺钉为不锈钢材料，骨架为铝合金材料，线圈部分比较复杂，本文振动台为水冷式振动台，驱动线圈由镁铝合金薄环、水管、铜制线圈以及环氧树脂组合而成，建模时将线圈视为实体结构。

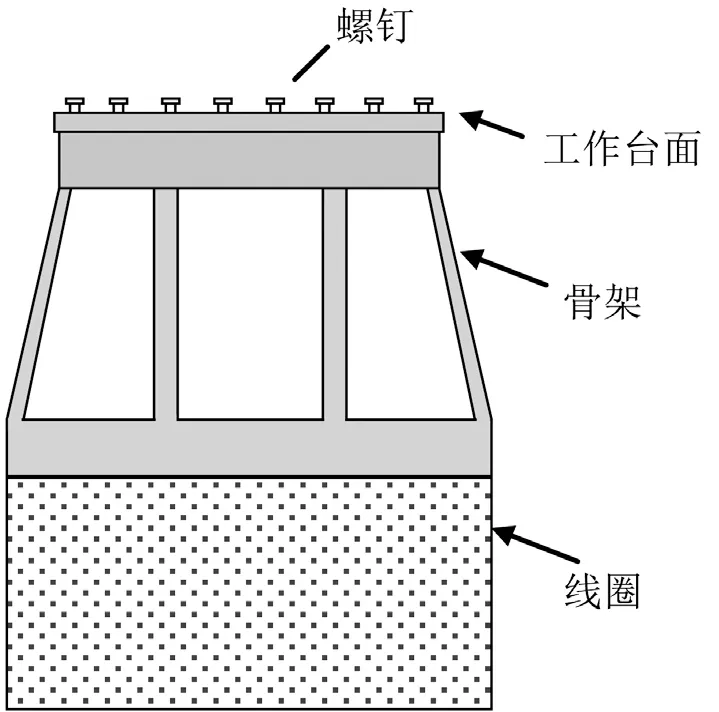
图1 动圈结构示意图

1.2 动圈模型修正

有限元是基于材料属性（杨氏模量、泊松比、质量密度等）和要模拟系统的物理尺寸进行求解的[7]。为建立更加准确的数学模型，需要对模型进行修正处理，动圈模型修正的主要原则是修正各部分结构的弹性模量、密度和质量，同时保证数值计算的固有频率和振型与模态试验的结果一致。模态试验数据是仿真模型修改的主要依据，修正结果的优劣将直接影响仿真的精度，其中动圈骨架和台面螺钉均可在材料参数手册中参数值附近进行查找调整，驱动线圈组成较为复杂，只能通过不断调整参数以达到与试验数据相近的结果。

1.2.1 动圈模态试验

自由模态反映的是试件固有的振动特性，最能反映结构的自身特点[8]。采用橡皮绳悬挂动圈模拟自由边界，以反映动圈的真实固有特性。根据动圈结构特点共布置88个三向测点，分别分布在动圈台面、骨架和线圈上，试验状态与模态测点布置如图2所示，使用多参考点移动传感器法进行力锤敲击模态试验。

图2 模态试验

1.2.2 模型修正

根据模型修正原则和模态试验结果，不断调整材料参数，适当修正模型边缘结构，最终动圈各个部分材料参数值确定如下：骨架密度为2 800 kg/m3，弹性模量为69 GPa；线圈密度3 000 kg/m3，弹性模量72.3 GPa。动圈重量为52.37 kg，实际重量为50.8 kg，误差为2.9 %。模态频率与振型结果如表1所示。

表1 试验与计算模态结果对比

根据模态结果与振型图可以看出，动圈一阶模态388.9 Hz，表现为肋板扭转。二阶与三阶、四阶与五阶均为对称模态，表现为线圈的呼吸扩张运动，前五阶误差均在5 %以内。其中一阶轴向共振频率影响动圈轴向伸缩运动并决定了振动台台工作频率的上限范围[9]，模态试验得到轴向一阶频率为2 080.6 Hz，修正后动圈的一阶轴向频率为2 207.2 Hz，误差为6.08 %，修正得到的动圈模型能够反映动圈的基本特征。

2 正弦振动仿真分析

2.1 激励施加分析

电动振动台的基本工作原理与扩音器原理类似，是基于载流导体在磁场中受到电磁力作用而运动。振动台台体中的励磁线圈产生恒定磁场，信号发生器产生交变信号，经过功率放大器后，输入到动圈，电磁力会在驱动线圈的绕组下产生，使得台面产生向上和向下的往复运动，电磁力 F = BIL[10]。其中 B 为恒定磁场中的磁感应强度（Wb/m2），L 为动圈绕线的有效长度（m），I 为动圈中的电流（A）。

台面在激振力F的作用下振动，振动幅值取决于电流I，对于给定的振动台，电流与电压成正比，因此可用力F来代替驱动电压进行激励，线性假设条件下，控制点响应A（f）、驱动线圈中的驱动力幅值F（f）、频响函数值H（f）存在以下关系：

以两点平均控制为例，需进行两次频响计算，先施加一定的激振力谱F1（f），获取台面控制点1和控制点2的响应B1（f）和B2（f），这两点的平均响应为：

此时由式（1）求出频响函数值H（f）=B（f）/F1（f），若实际振动给出的正弦振动条件为则新的激振力谱为：

2.2 正弦扫频仿真

振动台动圈通过工作台面的U型悬挂弹簧悬挂在振动台刚性台体上，悬挂弹簧均匀分布在工作台面下方的四周边缘，构成弹性支撑系统提供恢复力和支撑力，限制动圈旋转和摆动的作用，在ANSYS中约束弹簧连接部位节点，仅保留轴向自由度，动圈中央刚性轴限制动圈不必要的横向运动，在ANSYS中采用弹簧单元约束刚性轴底部，仅保留垂向平动自由度。以动圈台面两点平均控制为例，进行2 g状态下的正弦扫描振动，响应计算范围为（5～2 000）Hz，模态计算范围为（0～3 000）Hz。

在动圈驱动线圈表面任意施加600 N的激振力，进行第一次频响计算，计算得到台面控制点1与控制点2的加速度响应，如图3（a）所示，整体趋势与图3（b）电动振动台典型恒流幅频特性曲线一致，第一个谐振频率是由振动台的悬挂支承系统谐振而引起的，称为悬挂系统自振频率，第二个谐振峰是由于振动台动圈谐振引起的，为动圈第一轴向共振频率。

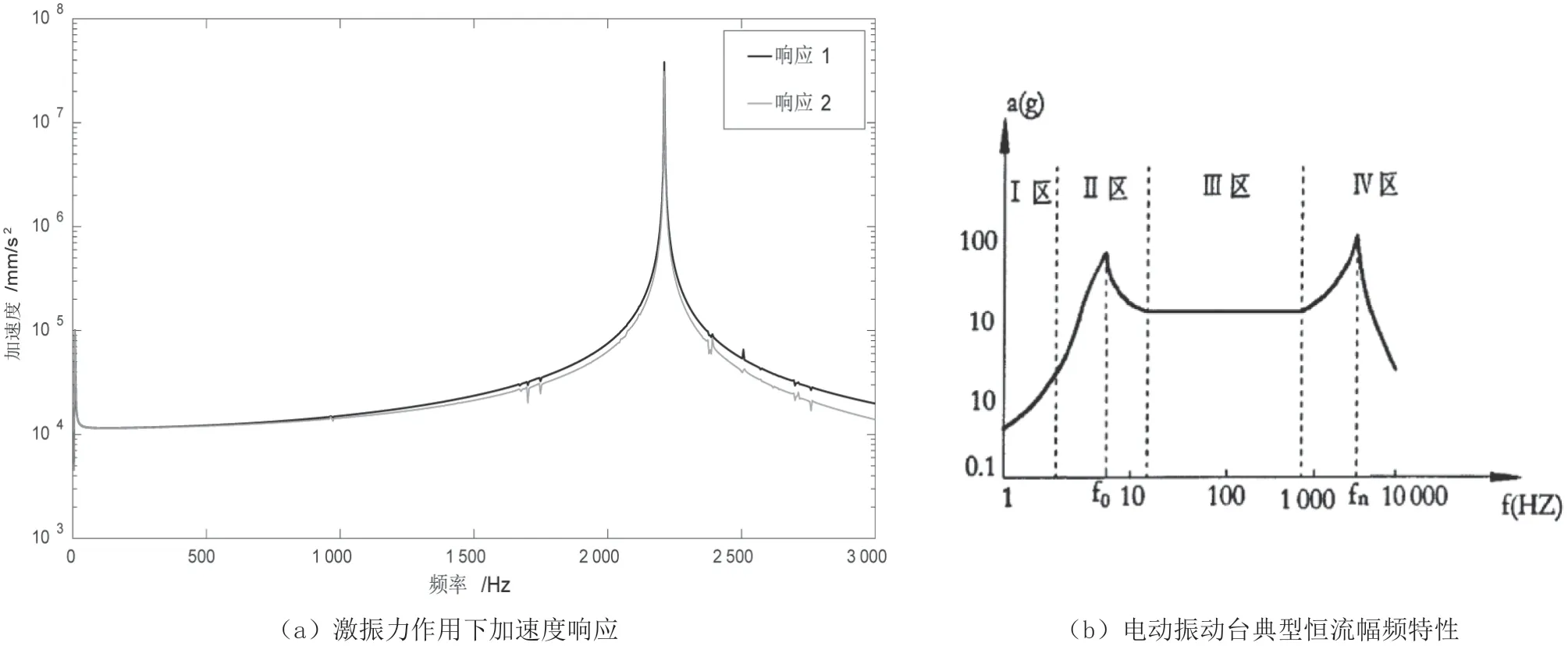
图3 幅频特性

根据得到的台面两点加速度响应的平均值和公式（3），可求出最终施加在驱动线圈上的激振力谱。经过力谱输入仿真计算，便可得到动圈台面两点加速度平均响应结果。

2.3 正弦扫频试验

图4为8 t振动台正弦扫频试验，点1和点2为振动控制点，点3、4为振动监测点，对台面进行频率范围（5～2 000）Hz的2 g加速度正弦扫频振动，控制方式为两点平均控制，试验粘贴测点位置与有限元模型测点位置尽量保持一致，将两点平均控制响应谱的试验结果与仿真结果进行对比，见图5，在（5～2 000）内的试验与仿真的加速度响应结果较为吻合，仿真的加速度值在2 g上下浮动，变化较小，可以看出仿真的精度较高。在1 700 Hz之前两者结果十分接近，1 700 Hz之后，试验结果出现一定波动性。

图4 扫频试验

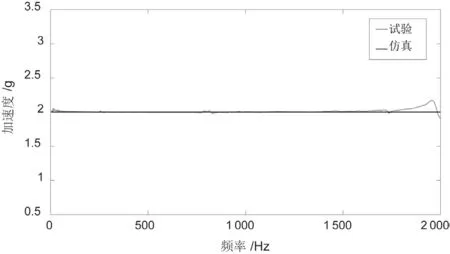
图5 两点平均控制响应谱结果对比

从图6和图7中可以看出，台面监测点3与监测点4的仿真结果曲线都较为平稳，而监测点的实验结果均在1 200 Hz后出现波动，这主要是因为振动台实际结构复杂，存在运动部件在高频段自身会发生弹性变形及局部振型等因素，虚拟仿真则有效避免了不均匀性的影响。

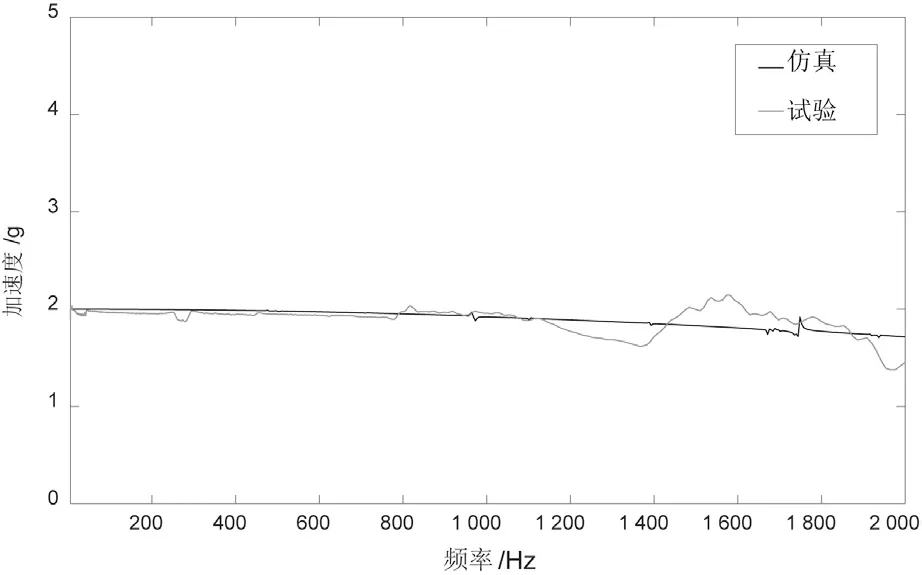
图7 监测点4加速度响应

4 结论

本文根据动圈实际结构与模型试验数据对动圈进行模型修正，修正各部分结构参数后使得模型有限元得到的前五阶固有频率与模态试验结果一致，误差在5 %以内，一阶轴向固有频率的仿真与试验结果较为接近，同时保证了质量和振型的一致性，建立了能够反映8 t电动振动台动圈特性的动圈有限元模型，根据动圈实际安装状态施加相应的边界条件，基于振动台工作原理，进行频响计算反推出2 g加速度正弦振动条件下施加在驱动线圈上的激振力谱，以该激振力谱为条件进行正弦扫频虚拟仿真，与实际扫频试验结果进行了对比，台面两个控制点得到的平均加速度响应值的仿真与试验结果较为吻合，虚拟仿真扫频能够较好的模拟出正弦振动试验结果。由于振动台结构本身的非线性等因素，正弦扫频试验部分监测点在高频段会出现局部的波动，而仿真在线性假设条件下避免了这些因素，仿真结果均很平稳，精度较高，但两者结果的整体趋势仍然一致，正弦振动虚拟仿真可以对扫频振动进行较好的预测。