面向变压器继电保护的励磁涌流分析及二次谐波制动保护

杨松，季华艳，张寅

（国网安徽省电力有限公司安庆供电公司，安庆 430030）

引言

随着近几年国家对于电力需求的大幅提升，电网系统的结构进一步完善，资源分配状况进一步合理，随着国家在维护和检测继电保护装置的发展不断进步，其运维效率也不断提升，在大数据崛起和电网系统逐渐成熟的背景下，如何有效利用海量数据对电网设备进行安全运维和保护检测就成了研究重点[1]。在电力系统的保护和检测中加入大数据分析，目的是为了在海量的状态测量值下，更为准确地进行状态检测和故障诊断，这对于电力系统日常工作中实现更高精度的测量要求[2]。目前我国在电力设备的重点研制计划之一，就是对变压器的能源消耗和设备精度进一步提高。电力变压器在过去几年的发展十分迅速，体积不断减小，效率不断提高，其作为设备网络之间的链接纽带，对电力电网系统的输电送电和安全运维有着重要意义[3]。

截至2018年，我国的国产变压器继电保护设备基本达到100 %，且运行时间达到7年以上的设备占比接近60 %。但是，变压器设备由于自身保护缺陷的存在，制造不良占比超过50 %。由于国家目前的研究重点放在了超高压和特高压电网系统的研制和发展上，变压器承担能量转化及输送的任务，对电网继电保护的稳定性和安全性具有重要意义。同时，提高电网系统的继电保护水平能够有效避免电网故障甚至系统崩溃等严重事故[4]。

在实际工程应用中，需要结合变压器电路原理和结构体系，充分考虑励磁电流，该现象容易造成变压装置和保护设备的差动保护误动，因此准确辨识励磁涌流的特征是保护变压器装置的重中之重。在传统的磁滞现象保护技术中，通常只是将铁芯磁化转化为较为简易的磁滞回线，该方法往往存在准确性较低、模型误差大等缺点，所以将磁化保护策略和材料等效模型加以考虑，能够进一步提高变压器的保护准确度和安全可靠性[5,6]。在材料等效模型方面，可以将物理定义清晰、参数特征明确的Jiles-Atherton模型加以考虑。对此，本文通过粒子群算法对Jiles-Atherton模型进行参数寻优，获得更为精确的B-H曲线，同时基于传统的差动保护方法与二次谐波制动方法进行融合，对变压器装置中的励磁涌流现象加以控制，解决变压器设备内部和外部故障，进一步探索不同温度下J-A改进模型保护设备的安全稳定性。

为了强化变压器设备的保护，解决内部和外部的故障问题，本文在传统J-A模型的基础上，采用能量等式改进模型，提高特征参数的识别效果；融合差动保护和二次谐波制动，对变压器内部和外部故障和励磁涌流进行精准识别和预警，最后验证了不同温度下J-A改进模型的有效性和稳定性。

1 J-A改进模型与参数智能识别

1.1 传统Jiles-Atherton模型

如果铁磁的内部磁畴运动存在无障碍位移，则可认为材料能量无损耗，其内外磁化强度相同，这就是无磁滞磁化[7]。因此，将Man和M分别表示为无磁滞下的磁化强度和外磁化强度：

式中：

a—定义曲线形状参数；

α—磁畴间耦合场参数；

He和Ms—有效磁场和饱和磁化强度。

采用Langevin函数表示磁化曲线：

当H = 0时Man= 0、当H = ∞时Man→ 1，存在：

若存在H = 0时Man= 0、H = ∞时Man→ 1，则磁化曲线变形为：

Jiles与Atherton定义磁畴壁弹性位移形成的非可逆磁化强度Mirr和钉扎效应形成的可逆磁化强度Mrev的总和定义为磁化强度：

磁化初期为无磁滞磁化（可逆磁化），真空磁导率μ0=4π×10-7H/m，由式（1）可得能量等式：

分别定义方向系数δ和牵制系数k，出现磁滞磁化的能量等式：

同时定义可逆磁化系数为c：

则式（5）转化为：

H与非可逆分量Mirr关系可表示为：

H与可逆分量Mrev关系可表示为：

H与磁化强度M的关系可表示为：

定义磁感应强度B，则磁滞回线为：

1.2 改进J-A模型

外电场在交变磁场中的铁磁材料上产生电流：

畸变磁通波形下，定义结构参数、叠片厚度和电导率分别为β、e和σ，总功率损耗为：

磁畴壁位移时，会感应出造成材料退磁的涡流。定义耦合常数G和耦合场参数V0，横截面积S，对这类额外损耗的表述为：

材料在实际工况下通常为50 Hz，则：

则额外损耗的变化表达为：

结合涡流损耗和额外损耗：

此外，引入温度系数Ti调整损耗和最大磁化强度，引入调整系数Ti= ((Tc-T0) /Tc)β1调整pe、pex、Ms的温度特性。定义居里温度和当前温度分别为Tc和T0，临界指数为β1，则：

1.3 PSO参数寻优

粒子群优化算法（PSO）基于位置和速度随机产生算法粒子，即可能解，通过适应度函数评估可能解。对于数值来说，寻优中的多个数值会聚合成一个点并通过最优解位置Pt和局部最优解Gt实时更新数值点的位置和速度。定义粒子速度和位置分别为v和x，迭代次数为t，加速因子和惯性因子分别为c（c1、c2）和ω，则调整公式：

调整位置和速度的运动为c1r1(Pt-xt)，与群体交流的调整运动为c2r2(Gt-xt)。在基于J-A改进模型的参数智能识别中，首先初始化粒子群的初始位置和初始速度，采用PSO获取空间局部最优解，通过多个局部最优解的对比进一步获取空间全局最优解。

1.4 参数智能识别

本文采用PSO算法对式（20）中的Ms、a、k、c、α、Ti进行参数寻优，以式（20）作为目标函数，并构建下式得适应值函数[8]。其中，磁感应强度的实验值和计算值（PSO寻优）分别为M实验n和M计算n，则适应值F表示为：

PSO寻优流程为：

1）基于PID应用经验，设定无干扰状态时的c1=c2=2，ω = 1，t = 250。由PSO设定初始值Ms、a、k、c、α、Ti，并将PSO寻优值前传至式（20）。

2）由式（20）和式（22）求得适应值F。

3）若F不满足输出条件则重复步骤（1）和步骤（2），若满足条件则输出最优参数。流程示意图如图1所示。

图1 PSO参数寻优流程示意图

2 二次谐波制动方法

2.1 磁滞回线

本文采取TDS3054C示波器通过实验获取参数智能识别的模型数据。表1为实验电路参数，表2为不同实验温度下PSO寻优参数值，表3为不同实验温度下的最大励磁强度值，包括实验测量值、传统J-A模型计算值和改进J-A模型计算值。

表1 实验电路参数

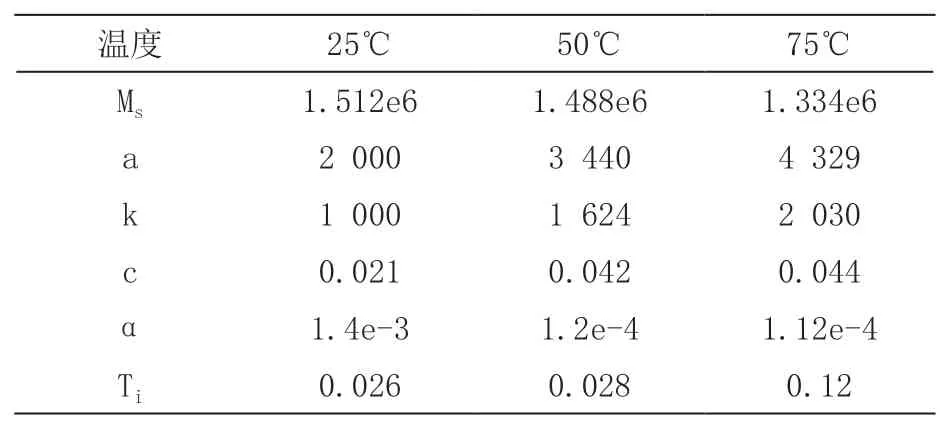
表2 PSO寻优参数值

表3 最大励磁强度值对比

采用J-A改进模型能够缓解能量不平衡，在表现铁磁材料的温度特性方面具有良好效果，克服了方向系数与磁化量变化不一致的缺陷。在温度较低（25 ℃与50 ℃）时，最大磁化强度差距不大，这表明变压器受低温度的影响不大；随着温度升高（75 ℃），最大磁化强度降低，造成了变压器铁芯退磁效果。对实验结果分析可知，J-A改进模型能够较好地捕捉温度对变压器材料的影响和铁芯损耗特性，反映出磁化过程，能够保证该方法在不同温度下的有效性和稳定性。

2.2 比率差动结合二次谐波制动

保护装置的内外故障在变压器空载时的励磁涌流中很难区分，由基波含量和二次谐波含量进行二次谐波判别[9,10]。由于二次谐波同样出现在严重短路的变压器内部区域，因此本文为消除保护元件拒动现象，加入了速动元件，加入二次谐波制动的原理图如图2所示。在二次谐波模型中，通过J-A改进模型根据温度变化调整经典磁化曲线，最终获取准确度较高的二次谐波制动比。

图2 比率制动与结合二次谐波制动原理图

3 变压器保护试验

3.1 变压器内部故障保护制动

本文对三个容量50 MVA、并联负荷5 MW/ 1 Mvar的三相变压器进行内部故障实验，设置两个35 kV的三相电源，频率为50 Hz，分别设置0 °、10 °的初相角。三个变压器参数分别为350 kV-0.2-0.08；5 kV-0.2-0.08；5 kV-0.2-0.08。故障信号设置为（0.3～0.5）s。

设置比率制动系数为0.5，一次侧和二次侧A相电流分别为Iam和Ian，当动作电流大于制动电流时，差动保护动作[11]。比率制动模块的参数如下：

差动电流：

制动电流：

分析图3可知，正常工况下的变压器由于低差动电流不发生保护动作。而在（0.3～0.5）s左右遇到A相接地短路、AB两相接地短路、AB相间短路、三相接地短路和匝间短路后，均由较大差动电流激发保护动作。对整体实验结果分析，不同类型故障均可设置为1，同时，保护装置无误动，正常动作。

图3 变压器内部故障波形图

3.2 变压器外部故障保护制动

本文对三个容量50 MVA、并联负荷5 MW/ 1 Mvar的三相变压器进行外部故障实验，设置两个35 kV的三相电源，频率为50 Hz，分别设置0 °、10 °的初相角。三个变压器参数分别为350 kV-0.2-0.08；5 kV-0.2-0.08；5 kV-0.2-0.08。故障设置在25 ℃下，（0.3～0.5）s。

分析图4可知，正常工况下的变压器由于低差动电流不发生保护动作。分析图4（a）可知，在（0.3～0.5）s左右遇到区域内三相短路故障后，立即出现制动保护动作。而分析图4（b）可知，在（0.3～0.5）s左右遇到区域外三相短路故障后，变压器由于低差动电流不发生保护动作。

图4 变压器外部故障波形图

3.3 结合J-A模型的变压器励磁涌流制动

内外故障保护均具有良好性能。在变压器空载时，采用J-A改进模型进一步考虑励磁涌流，添加二次谐波制动模块，修正磁化曲线。故障设置在不同初相角下，时间在（0.3～0.5）s，并设置0.02 s的二次谐波延迟判定时间。二次谐波在不同初相角下的含量如表4所示。

分析表4可知，二次谐波在不同初相角占据主导地位。考虑到A相谐波占比呈明显波动状态，所以要采取其他相过高的二次谐波判别励磁涌流。对比分析差动保护和比率差动结合二次谐波制动的实验结果，进一步探索J-A模型的有效性和可靠性。

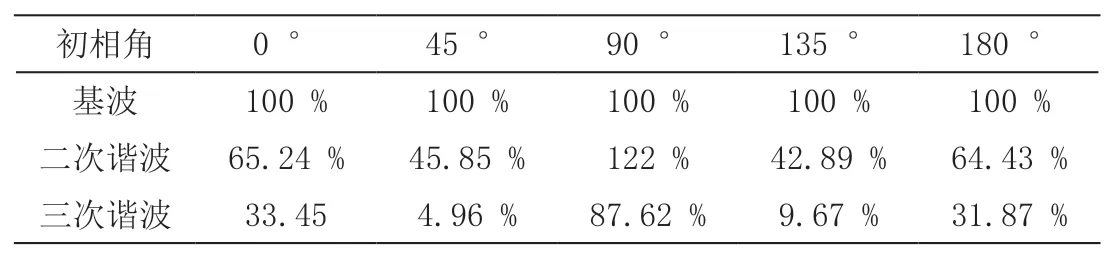
表4 二次谐波在不同初相角下含量对比

1）初相角0 °

图5为在初相角0 °时，不同温度下的变压器故障信号波形图。分析图5可知，变压器在25 ℃、50 ℃和75 ℃时空载进行合闸，合闸后的（0.3～0.5）s在区域内均出现三相短路，出现差动电流保护。加入二次谐波制动，动作信号只在短路故障后才出现保护动作，而励磁涌流时并无动作，能够准确避免励磁涌流误动；无二次谐波保护则出现误动现象。不同的是，温度越高，二次谐波比越低。

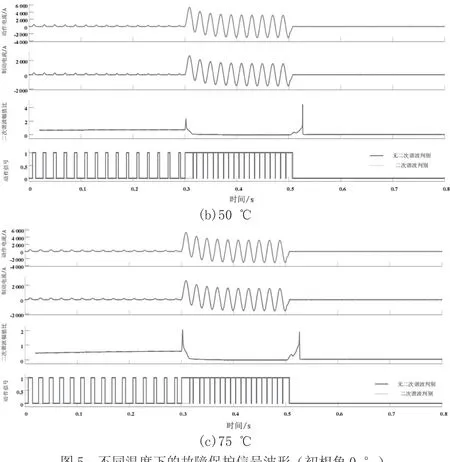
图5 不同温度下的故障保护信号波形（初相角0 °）

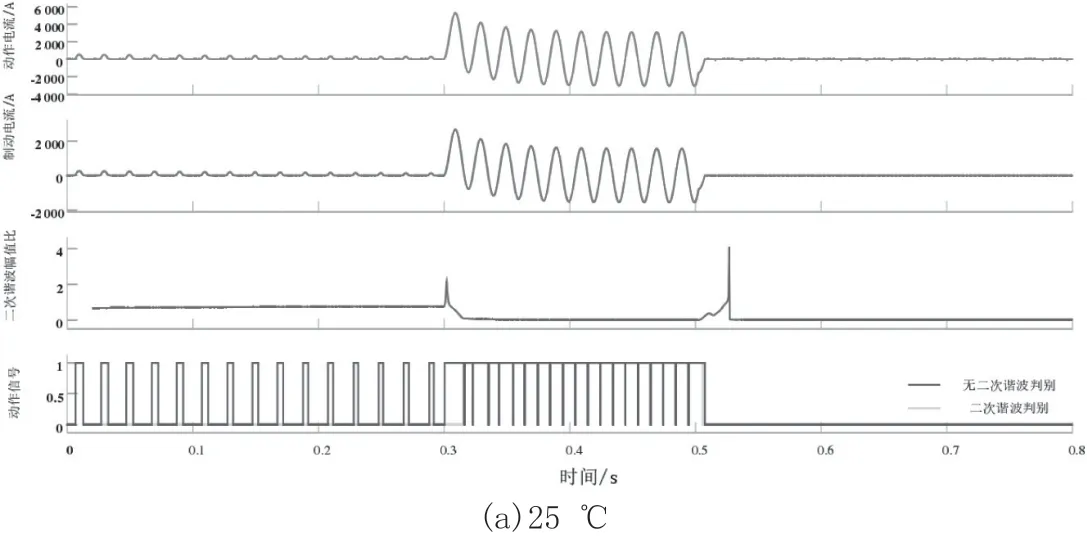
图5 不同温度下的故障保护信号波形（初相角0 °）

2）初相角45 °

图6为在初相角45 °时，不同温度下的变压器故障信号波形图。分析图6可知，变压器在25 ℃、50 ℃和75 ℃时空载进行合闸，合闸后的（0.3～0.5） s在区域内均出现三相短路，出现差动电流保护。加入二次谐波制动，动作信号只在短路故障后才出现保护动作，而励磁涌流时并无动作，能够准确避免励磁涌流误动；无二次谐波保护则出现误动现象。不同的是，温度越高，二次谐波比越低。

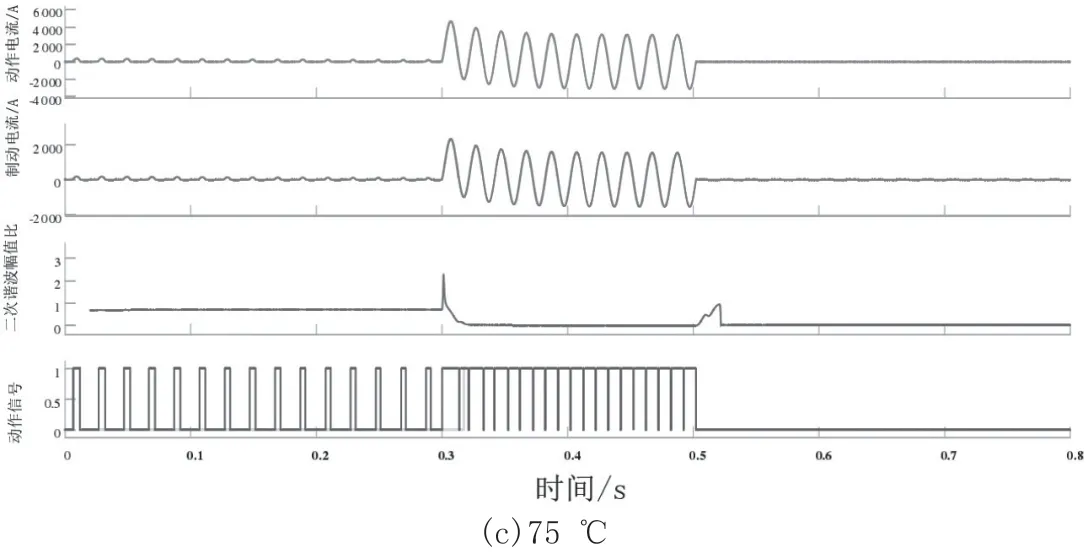
图6 不同温度下的故障保护信号波形（初相角45 °）

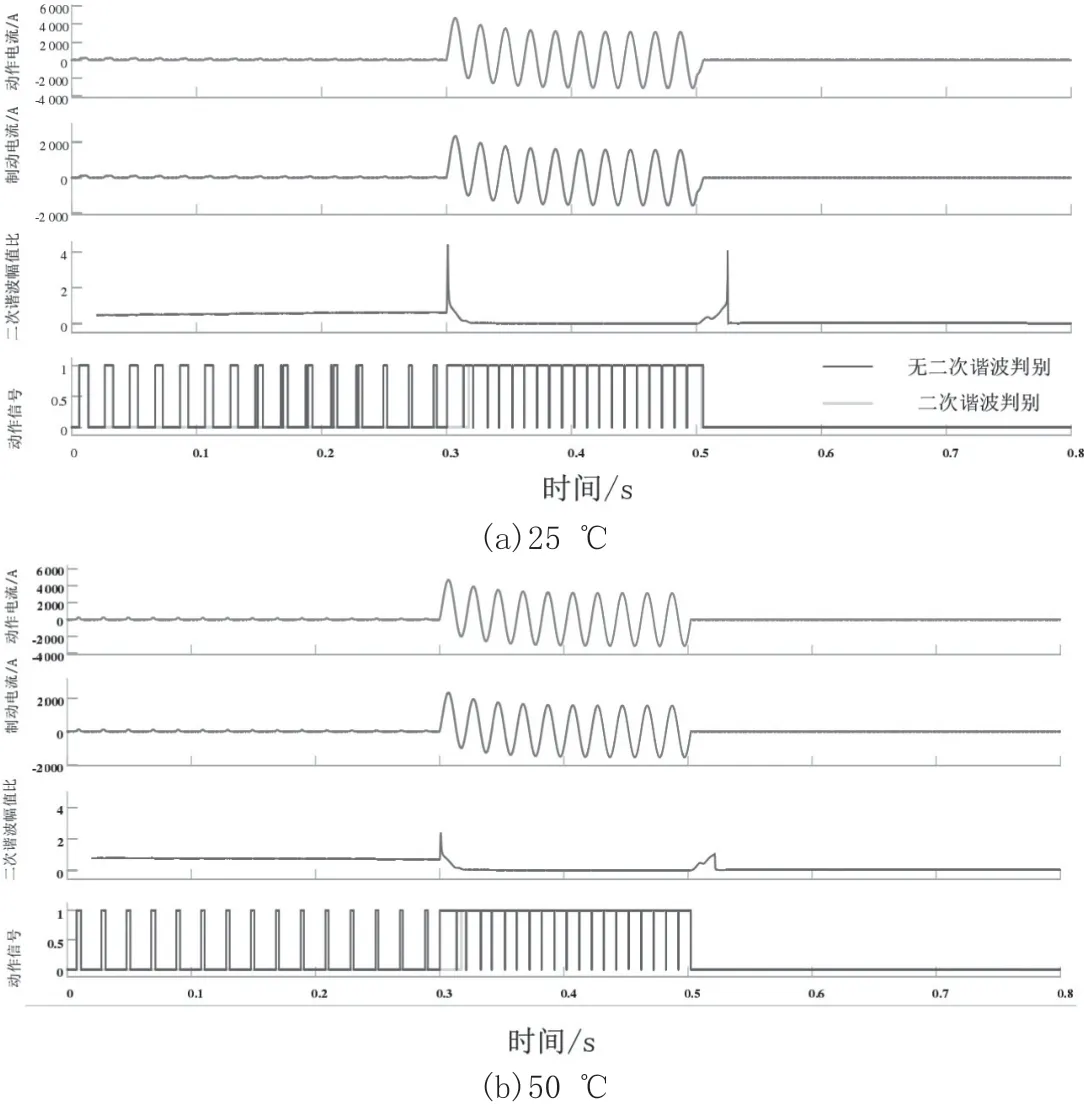
图6 不同温度下的故障保护信号波形（初相角45 °）

引入J-A改进模型，对不同初相角、不同温度时的变压器故障进行实验。实验结果如图7所示。图7为初相角0 °、45 °、90 °下，25 ℃、50 ℃、75 ℃时的二次谐波比波形图。分析图7可知，二次谐波与基波的比值与温度呈正相关关系，温度越高，二者比值越低。而在二次谐波比方面，25 ℃、50 ℃时随时间增加而下降，75 ℃时随时间增加而上升。

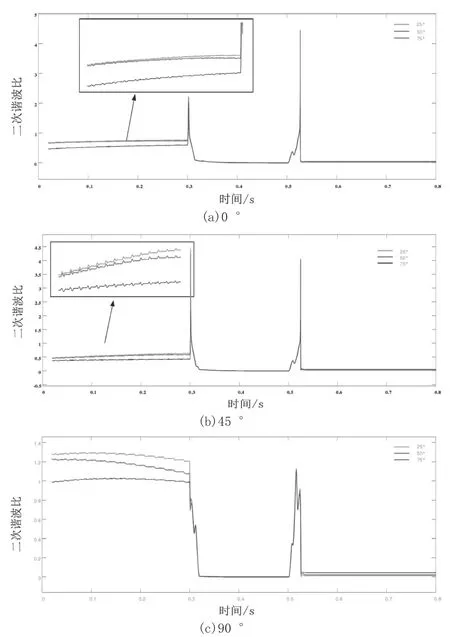
图7 不同初相角下二次谐波制动对比

对前文分析得知，不同温度下，在初相角0 °、45 °中引入J-A改进模型能够获得正确的保护策略。对不同温度下的二次谐波比分析得知，温度升高到一定限度后，变压器铁磁材料会出现磁化过程被破坏的情况，也会影响变压器的保护动作。

4 结论

本文对变压器保护装置进行励磁涌流分析，并对保护方法进行研究，得出以下结论：

1）在传统J-A模型中引入涡流损耗和额外损耗，在数学模型中引入PSO算法智能识别特征参数，提出J-A改进模型，解决了能量不平衡缺陷；

2）在原有的差动保护基础上，结合了二次谐波制动，采用J-A改进模型分析变压器磁滞过程；

3）采用J-A改进模型提取二次谐波，对比分析不同制动保护方法的实验结果，进一步探索J-A改进模型在不同温度下保护动作的有效性和可靠性。实验表明，二次谐波与基波的比值与温度呈正相关关系，温度越高，二者比值越低。而在二次谐波比方面，25℃、50 ℃时随时间增加而下降，75 ℃时随时间增加而上升。引入J-A模型能够自行调整二次谐波制动系数，有效防止励磁涌流误动，准确反应实际应用中的温度影响。