汽车制动舒适性建模与控制
赵明强,吴宇轩,李弘志
(长安大学 汽车学院,陕西 西安 710064)
近年来,人们开始越来越关注汽车舒适性,其已经成为评价汽车性能一项重要指标。制动是行驶过程中的一种常见工况,汽车频繁制动会导致乘员舒适度降低。车辆在制动时,乘员感到不适主要发生在两个阶段:制动力突然增大造成的车辆俯冲和惯性力突然消失造成的汽车后仰。为了改善汽车舒适性,人们希望找到一种控制方法,减小制动时的俯仰。
汽车舒适性自21世纪以来一直备受学术界的关注,而制动俯仰很大程度上受到悬架与制动力大小的影响。
关于制动系统的进步创新稍晚一些,1996年,德国BOSCH公司与 Daimler-Chrysler公司共同开发了最早的一款电控液压制动系统(Electric Hydraulic Brake, EHB)[1],该系统能实现前后轮制动压力的分配跟随路况而变化,以此保证弯道制动时的完全性与舒适性。
我国研究主动悬架与半主动悬架起步时间比较晚,和西方发达国家相比有着不小的差距。但是,国内不少的院校与汽车工业研究所对主动悬架的控制策略进行了大量的研究,在他们的努力下,我国的主动悬架与半主动悬架技术取得较大的发展。比如厦门金龙、丹东黄海等客车厂家生产的大型铰接快速公交(Bus Rapid Transit, BRT)城市客车均采用了一种新配置电子控制空气悬架。霍书豪[2]针对非紧急制动过程中的车身俯仰运动,提出一种基于Skyhook控制原理的比例-积分-微分(Proportion Integral Differential, PID)控制算法,来控制制动过程中的俯仰角变化达到汽车舒适性模型。董德志[3]针对线控制动与半主动悬架制动工况对线控制动系统参数辨识与轮缸压力控制器设计。另外不少学者也在通过研究控制动力提高制动舒适性,龚贤武等[4]制动稳定性要求和ECER13制动法规的理想安全制动范围的情况下,引入变比例阀液压分配线来代替理想的制动力分配曲线,得出适用的制动力分配范围。郭金刚等0综合考虑电功率等影响因素的限制,结合安全制动范围进行制动力分配。
1 汽车制动俯仰模型的建立及分析
本文主要研究车辆纵向及垂向的动力学特性,忽略车辆的侧向动力学特性、车辆左右两侧的差异性、空气阻力、车轮旋转动力学、地面不平度。因此,本文采用1/2汽车模型,前后车轮各一个,车辆各个轴的左右车轮的贡献相等。簧上质量模型如图1所示。
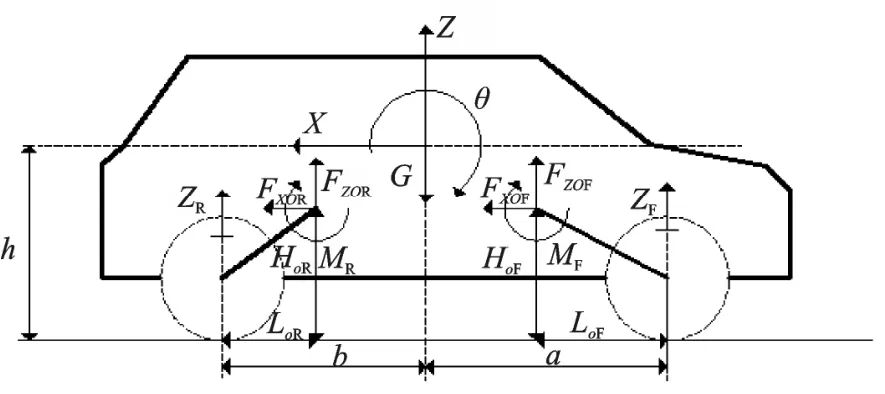
图1 簧上质量模型
汽车制动减速度表示为
整个汽车前后轴处的位移和速度可以表示为
式中,a为质心到前轴的距离;b为质心到后轴的距离;ZR为后底盘位移;RZ˙为后底盘位移速度[6];ZF为前底盘位移;FZ˙为前底盘位移速度;Z为底盘位移; 为底盘位移速度;θ为底盘俯仰角;θ˙为底盘俯仰角速度[7]。
因为θ比较小,所以可以近似计算为
由此得到简化后的公式为
根据几何学,前后悬架的旋转角度与旋转角速度可以计算为
由于前后悬架的旋转角度较小,可以近似计算为
同理旋转角速度也可以近似计算为
悬架扭矩M可以计算为静止时重力引起的扭矩与悬架弹簧力与减震器力引起的扭矩。其中MF,MR为前后悬架扭矩。后悬架扭矩为
式中,kF,kR为前后悬架的扭矩刚度;cF,cR为前后悬架的阻尼系数;kF,kR,cF,cR由悬架的弹簧刚度与阻尼系数等效而来,计算方法如下:
M为悬架弹簧力与减震器力引起的扭矩,即悬架垂直力F引起的扭矩;F为弹簧力与阻尼力的合力,即
式中,Kf、Cf为前后悬架弹簧刚度与阻尼系数,此时将在悬架的俯仰中心处对F取力矩M,即[8]
将式(7)、式(8)代入式(12)可得
由此可得等效后弹簧刚度与阻尼系数计算公式为
式中,L0F为前悬架俯仰中心到轮胎接地点的水平距离。
同理也可由此推导出后悬架等效后的弹簧刚度与阻尼系数为
式中,L0R为后悬架俯仰中心到轮胎接地点的水平距离。
从围绕质心的力矩平衡得到俯仰角加速度的运动方程为
式中,J为汽车绕质心y轴的转动惯量;L0F、L0R为前后悬架弹簧与车身的连接点到前后悬架俯仰中心纵向的距离;H0F、H0R为前后悬架弹簧与车身的连接点到前后悬架俯仰中心的垂直距离。
车身垂直方向的振动方程为
图2为簧下质量模型,对于簧下部分图2(忽略簧下质量)进行分析,即
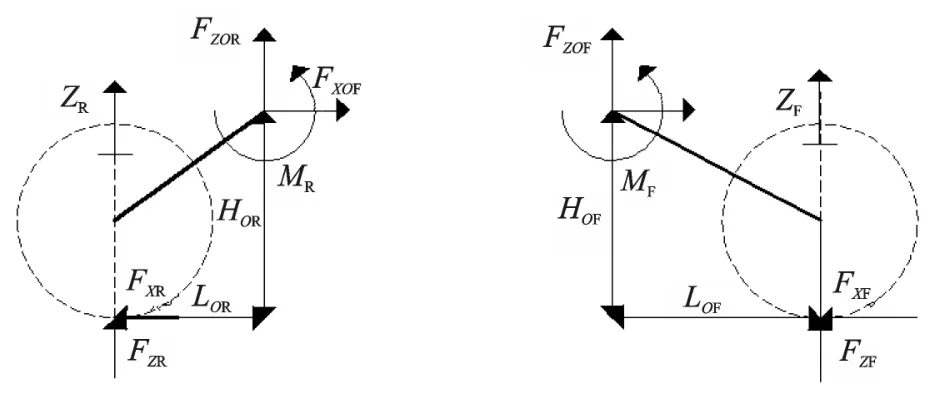
图2 簧下质量模型
根据前后悬架纵倾中心处的力矩平衡,可以得到
根据此动力学模型,将式(5)、式(6)、式(8)—式(11)、式(13)、代入(12)可以得到以下汽车俯仰角方程[9]为
将式(5)、式(6)、式(8)、式(9)、式(15)代入式(13)得到汽车质心的垂直振动方程为
汽车制动俯仰模型仿真分析如下:
用Simulink搭建模型进行仿真可以得到俯仰角仿真图,如图3所示。汽车参数如表1所示。
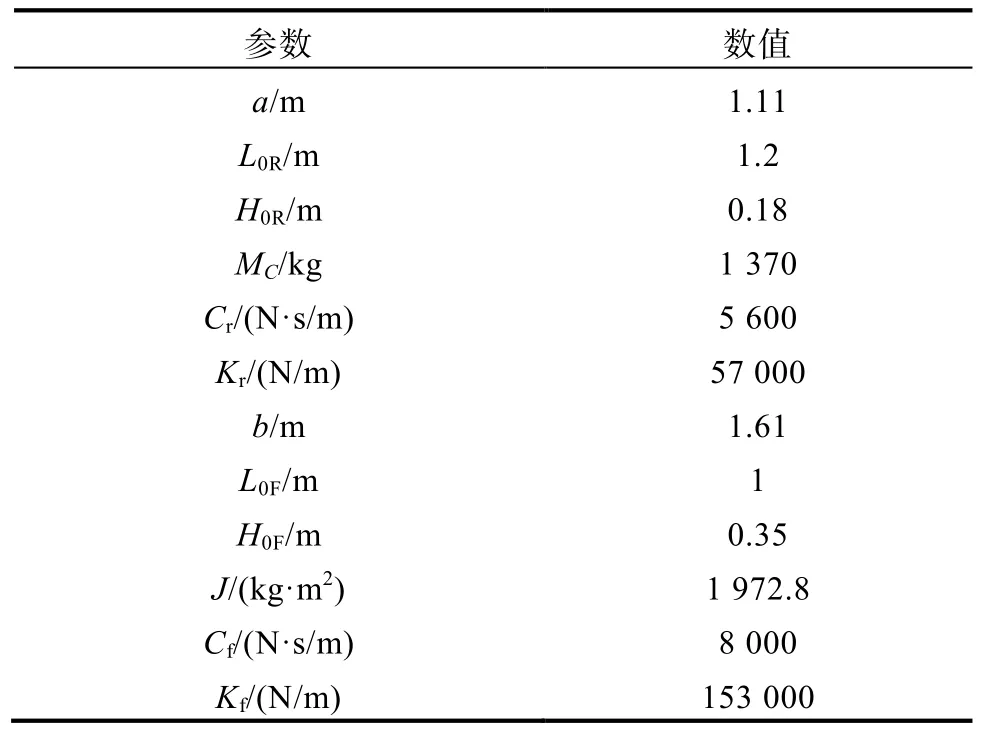
表1 汽车参数表

图3 俯仰角仿真图
以汽车静止状态为初始状态,此时俯仰角、俯仰角加速度、俯仰角速度、垂直位移、垂直位移速度、垂直位移加速度都为0。设定仿真时制动减速度为
将制动初速度设置为20 m/s,制动分配系数设置为0.34[7]。由仿真结果可以得知制动力突然增大造成的车辆俯冲,俯仰角会先增大,然后到达一个稳定值0.23°。随着速度的减小,当制动减速度为0时,惯性力突然消失造成的汽车后仰,由于惯性力突然俯仰角消失回弹到0°。
在汽车制动过程中,汽车会出现由于惯性力造成的轴荷转移的现象。由于汽车的轴荷转移,此时前后悬架所受的车身垂直力突变,前后悬架的弹性元件会有形变量产生,汽车产生俯冲,简单来说就是动态力使汽车俯仰[11-12]。由于悬架的弹性元件的作用,前后悬架会产生受到来自车身,导致悬架的前后产生不同悬架挠度而引起的悬架力,这部分不同大小的悬架力会以悬架力矩的形式作用在质心,以此对抗地面作用力矩导致的车辆俯仰,以试图达到车身的平衡状态。而减加速度消失后,这个平衡又被破坏,悬架等弹性元件又会试图恢复形变,再次对车辆进行力矩做功产生后仰振动。
为了更好地分析制动俯仰过程,可以根据汽车的俯仰角响应,将整个制动俯仰过程分为三个部分制动前期、制动中期、制动后期。
2 制动俯仰的调节控制
霍书豪[2]对于同一制动强度的不同制动阶段做了研究,制动初期的平顺性与制动中期的平顺性相当,或者稍差与后者;而制动后期的平顺性则明显比前两个阶段要差。因此,将调节的重点放在制动后期。对于制动前中期,出于对制动安全性的考虑,不改变制动力大小,选择通过调节制动力分配系数来减小俯仰角。在制动后期,汽车的后仰是由于制动力突然消失造成,此时只调节制动力分配系数无用,对于制动后期,应该找到一种控制前后轮制动力的方法优化汽车的俯仰。
本文对制动中期进行俯仰优化,发现要使稳定时的俯仰角最小,应该使得制动力分配系数最大,汽车俯仰的状态空间模型为
列出系统哈密尔顿函数为
根据上述条件用Matlab求解λ,得到
要得到最优控制,应该使前轮制动力系数uF保持最大。但是极小值原理只是给出了目标泛函取得极值的必要条件,而不是充要条件。为了验证探究是否使得目标泛函达到极小值,本文在Simulink中进行仿真验证,得到制动前期俯仰角对比如图4所示。为了直观验证控制是否有效,将使用极小值原理控制后得到的俯仰角与保持制动力恒定的工况下的俯仰角进行对比。

图4 制动前期俯仰角对比图
可以发现,在满足制动中期最小俯仰角的情况下,采用此控制可以达到控制目的。虽然在前0.2 s时,控制后的俯仰角稍大一点,但是相差不多,同时使得制动前期的俯仰角波动减小,达到了控制的目的。因此,该控制方法可行。
2.1 无限时间状态调节器的设计
前后制动力变化如图5、图6所示,通过对比使用线性二次型调节器(Linear Quadratic Regul- ator, LQR)控制,消除俯仰回弹现象,同时使得制动俯仰角较平缓,此时制动俯仰角会在3 s内缓慢变为0,大大提高了制动后期的舒适性。使用LQR控制器虽然减小了俯仰角加速度、俯仰角、冲击度的大小,但还是使得冲击度大于评价标准。为了保持制动安全性,本文选择在速度为1 m/s的时候进行控制,此时制动力虽然不是突变为0,但也会在短时间内减小,如果想要减小冲击度,可以选择将控制时的初速度变大。但会使制动距离增加。但考虑对于轿车而言,冲击度的影响较小,所以不再过多优化冲击度。用此LQR控制会使制动距离会增加0.25 m,占制动总距离的0.62%。这是可以接受的。

图5 前轮制动力变化
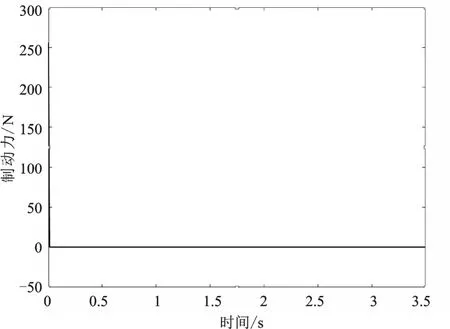
图6 后轮制动力变化
对于制动初速度较低时,不推荐使用控制器,因为此时制动距离比较短,使用控制器可能会使制动距离增大几倍,容易发生碰撞。在控制中,更加重要的是,在制动工况减速的最后一段时间之内,虽然增加的制动距离对驾驶员来说几乎是不可见的,但是使用LQR无限时间状态调节器时的初速度应限制在一个低-中速度范围内,以避免在紧急制动事件中产生较长的制动距离,降低制动的安全性。
对于此LQR控制器,最为重要的是权重Q的选择,对于不同的车型与不同的制动减速度,Q的选择也不一样。总体来说,俯仰角速度θ˙分配最大权重,速度v分配大权重,前后轮制动力也分配一定的权重(制动力越小,权重越高)。如果要使制动距离变短,应使速度v权重变大,如果要使俯仰角变化较平缓,应该使得俯仰角速度θ˙权重更大。权重的具体选择取决于对控制的要求。图7为俯仰角随时间变化趋势图。
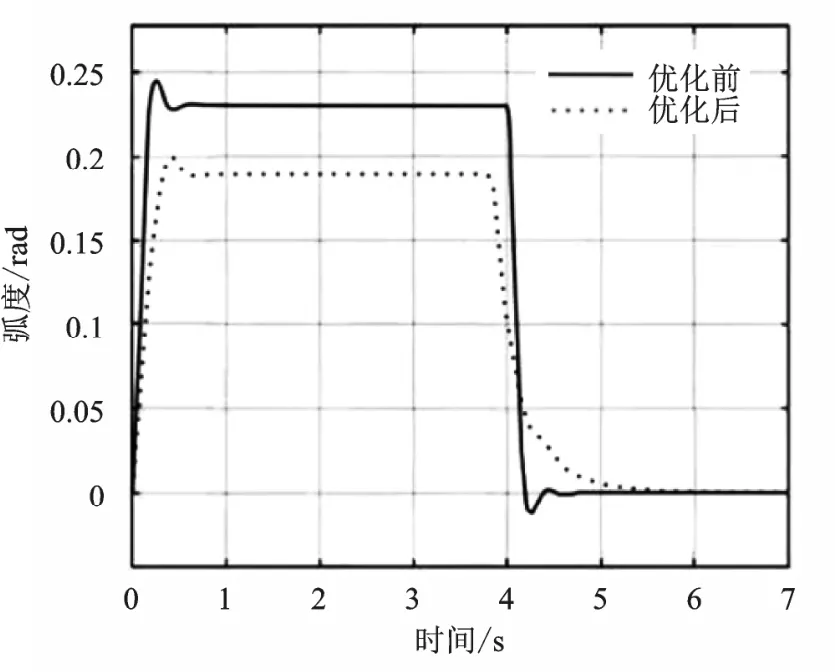
图7 俯仰角随时间变化
2.2 LQR线性参数调节
LQR线性参数调节类似PID控制器参数调节,凭借经验调节,对比不同参数下的数据选取一个最优方案。调节过程中不同参数下的俯仰角变化不同,仿真得出图像平滑性不同,选取出一个俯仰角最为平滑的数据即可。
3 总结
本文通过分析简化汽车制动俯仰模型,找到影响制动俯仰的关键因素,并用俯仰角、俯仰角加速度、冲击度评价俯仰舒适性。同时设计了一种制动力调节方法,优化制动俯仰角。在制动前中期,通过调节制动力分配系数,减小制动俯仰角,该方法未改变汽车总制动力大小,保证了制动安全性。
对于制动前期,以包含uF,uR的分数项作为输入,得到系统的状态方程。再利用极小值原理,求出在约束下的最优控制,使得俯仰角最小。
在制动中期,通过对微分方程的推导整理,找到使稳定时俯仰角最小的制动力分配系数,达到优化的目的。但是当制动力达到极限时,控制器不起作用。
对于制动后期,在速度为1 m/s时,采用LQR控制实现最佳制动力控制,消除制动回弹现象,并使俯仰角变化较平缓,但由于改变了制动加速度,会使得制动安全性有一定降低。在汽车制动速度较低时不推荐使用,以免发生碰撞。
文章也有一些待改进的地方,比如在模型上,忽略了簧下质量、轮胎动力学,会导致与实际的模型有偏差,默认地面水平,忽略了地面的不平度对俯仰的影响。由于简化汽车的振动模型,必然使得仿真结果与实际结果有所误差。但对汽车制动时整车俯仰振动的优化,仍然具有参考的意义。在控制器上,LQR对模型的精度要求比较高,如果传感器测量值的误差较大会影响控制,导致控制系统优化效果不佳,可以考虑设计卡尔曼滤波器,传感器测出的观察值与系统预测的预测值计算出一个较准确的真实值,使LQR无限时间状态调节器的控制效果更好。对于不同的情况,Q权重的选择都不一样,需要根据经验不断调试,这是一个十分繁琐的过程。不过,从Simulink的仿真结果来看,优化后的俯仰角有一定的减小,如果想更进一步地优化俯仰,可以考虑在控制动力得到最小俯仰的条件下,通过控制悬架刚度与阻尼。

