复杂层状土层地质对堤岸渗流特性的影响研究

王海龙，杜宁宇，王一朵

(1.江苏省地质局，江苏 南京 210000；2.河海大学河海里尔学院，江苏 南京 210098；3.河海大学土木与交通学院，江苏 南京 210098)

0 引言

随着大坝构筑物的发展，大坝渗流及稳定性研究得到越来越多的重视[1]。水库建成蓄水后，在上、下游水位作用下，坝体和坝基均会出现渗流现象，进而影响坝坡稳定性[2]。韩文娟[3]通过建立均质坝体模型，研究了坝体土料不同渗透系数在水位下降条件下的坝体浸润线和上游逸出点渗透坡降的变化规律，岳庆河等[4]深入分析了在水位下降时坝体材料渗透系数大小以及渗透系数的各向异性对大坝渗流及稳定的影响，李子阳[5]基于饱和-非饱和渗流理论，考虑了渗透系数与基质吸力的非线性关系，研究大坝非稳定渗流场和渗透稳定性的变化规律，坝体材料的渗透系数大小及渗透系数的各向异性会不同程度地影响大坝的渗流及稳定性，为此钟学梅[6]对两个影响因素进行敏感性分析，在此基础上，王宁[7]研究了坝体土体参数对大坝渗流及稳定的影响，包括土体渗透系数大小以及强度参数。

在实际工程中，坝基的地质条件并不是单一均质的，以上众多学者[8-10]在研究大坝渗流分析模型中，仅将坝基作为同一种材料来考虑，忽略了坝基的复杂地质情况。以合肥市大房郢水库为例，该工程沿坝轴线方向的长度较长，沿坝轴线方向的土层分布也发生变化，不同断面位置的地质条件存在差异，如分层土层种类、土层厚度以及土层起伏等。由于各土层渗透性的差异，不同土层分布将对大坝渗流产生不同的影响。因此，建立复杂的坝基地质条件模型更加符合实际情况。本文以合肥市大房郢水库大坝为依托，基于现场监测结果，通过数值模拟研究不同库水位下复杂地质条件对大坝渗流及稳定性的影响。

本文采用饱和-非饱和渗透模拟分析，根据饱和-非饱和渗流理论，开展二维有限元数值模拟，通过二维数值模拟，得出复杂地质对大坝渗流影响的一般规律。

1 模拟几何模型

图1展示了合肥市大房郢水库工程堤岸的计算模型。

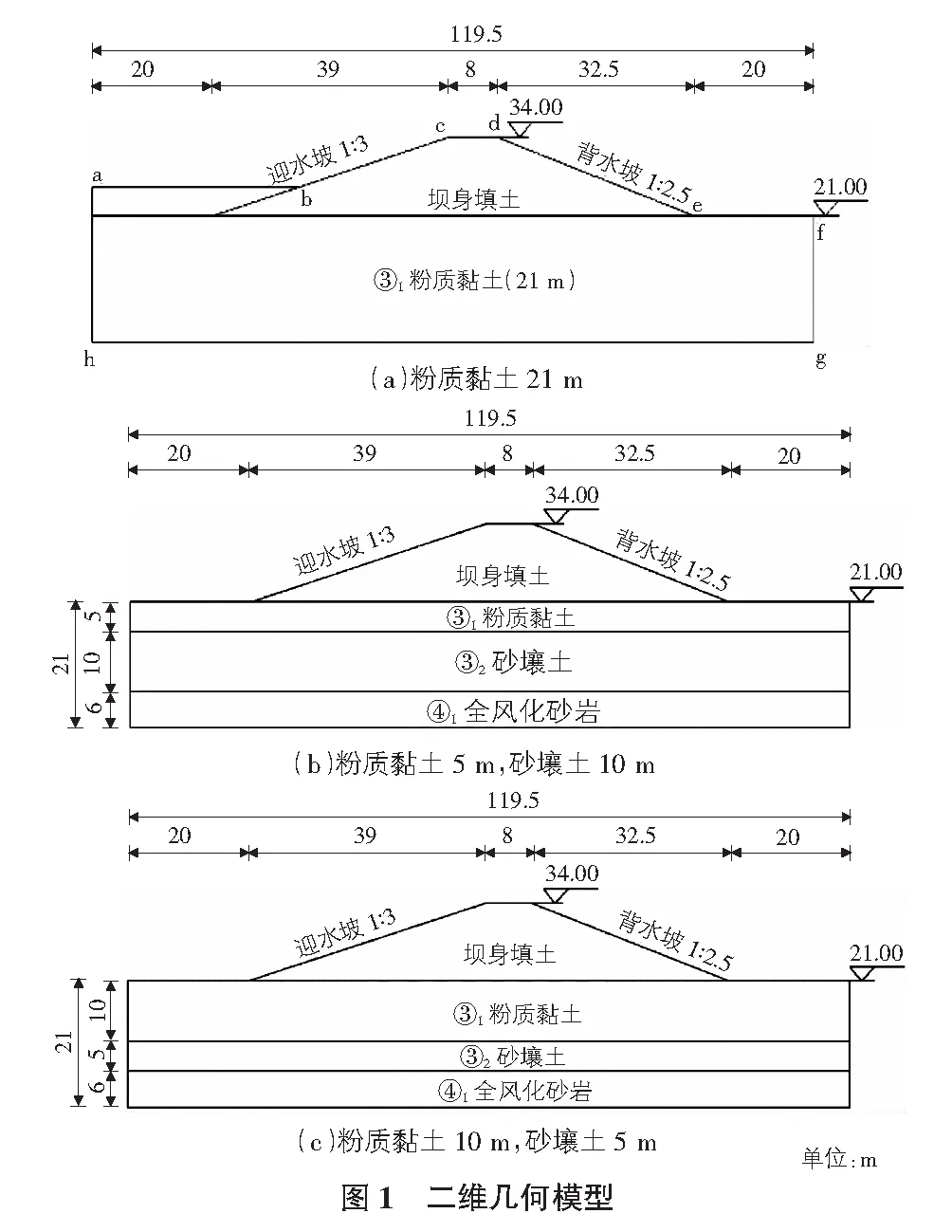
图1中坝高为13 m，上游坝坡比为1∶3，下游坝坡比为1∶2.5，上下游坝坡脚外延伸的长度为20 m，将下游坝脚外延伸的长度分别取20 m,30 m，以研究模型尺寸对渗流结果的影响，结果表明，当下游坝脚外延伸的长度为20 m,30 m时的渗流场变化一致，因此在不影响大坝渗流场的情况下，取最小下游坝脚外延伸长度为20 m。

2 土体参数

大坝为碾压式土坝，坝体材料的各向异性比值为4，即坝身填土水平向渗透系数与竖直向渗透系数比值为4，坝基老填土的水平向渗透系数与竖直向渗透系数比值为1.1，坝基其余土层水平向渗透系数与竖直向渗透系数相同。大房郢水库大坝各土层的土体物理力学性质指标见表1。

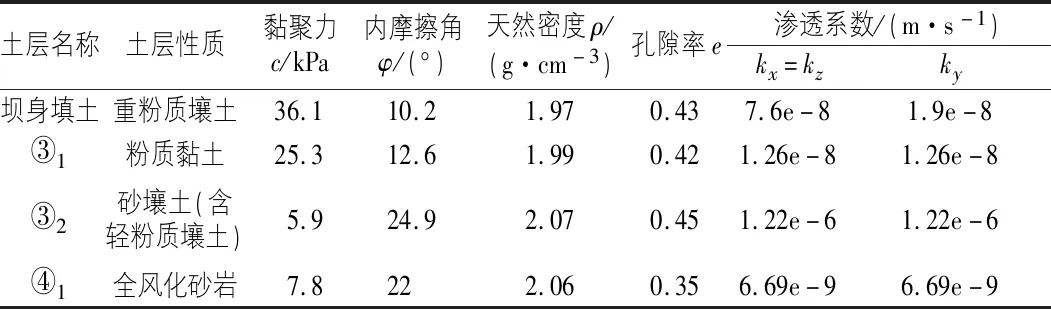
表1 大房郢水库土层分区及主要参数

由主坝纵剖图及各土层物理力学性质指标可知，大房郢水库大坝地面线以上即坝体部分土层较为一致，均为渗透系数较小的填土层，地面线以下土层均含有老填土层，其渗透系数大于填土层的渗透系数，而老填土层以下的坝基土层较为复杂，坝基地质条件复杂性体现在坝基含有②1～③2土层不等，且各土层的位置和厚度不同，它们的渗透系数差异较大，而坝基的最底层即相对不透水层均为④1层全风化砂岩，该土层的渗透系数很小。综上可将此复杂土层简化为三个断面进行计算。

3 边界条件

二维边界条件如图1(a)所示，图中ab为水头边界条件，de为下游坡面，设置为自由渗出面，坝基底部hg及坝基两侧设置为不透水边界条件，此边界的流量为零，下游边界ef为自由渗出面，设置为流量边界条件。

4 模拟结果分析

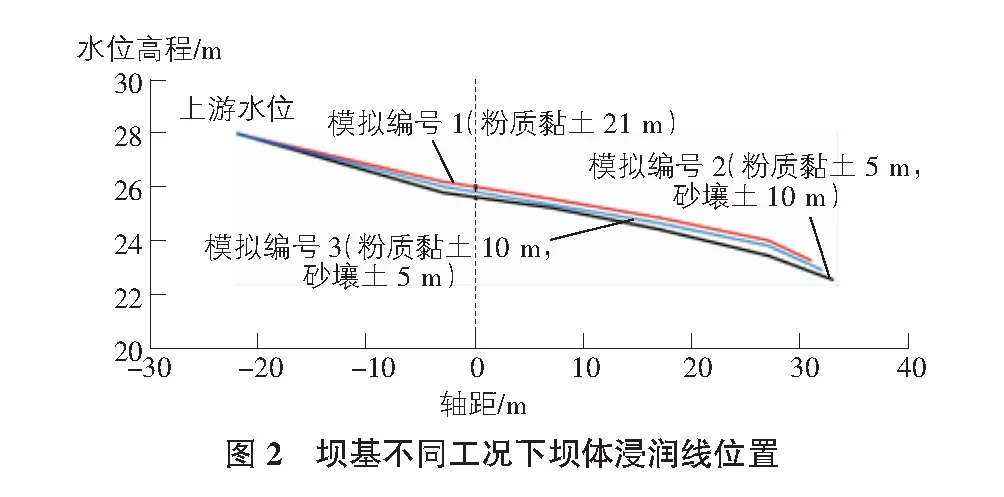
4.1 坝体浸润线变化

坝基不同工况下坝体浸润线如图2所示，图2中虚线表示大坝中心线即测线的所在位置。模拟编号1坝基为均质粉质黏土21 m，模拟编号2坝基为粉质黏土5 m砂壤土10 m的层状土层，模拟编号3坝基为粉质黏土10 m砂壤土5 m的层状土层。坝基为均质土层与层状土层的坝体浸润线有一定差异，坝基为均质粉质黏土的坝体浸润线最高，在层状土层坝基中，坝基较上层粉质黏土厚10 m的坝体浸润线高于粉质黏土厚5 m的坝体浸润线。由图3测线处孔隙水压力变化可知，测线处均质粉质黏土坝基的浸润线高程较高，坝基为粉质黏土厚10 m的浸润线高程次之，坝基为粉质黏土厚5 m的浸润线高程最低。具体表现为：测线处均质粉质黏土的坝体浸润线高程比层状土层坝基中粉质黏土厚10 m的坝体浸润线高0.14 m；层状土层坝基中，粉质黏土厚10 m的坝体浸润线比粉质黏土厚5 m的坝体浸润线高0.16 m。表明与均质土层坝基相比，层状土层坝基的浸润线高程低0.3 m左右，在层状土层坝基中，坝基较上层的下卧阻水层厚度增大、下卧导水层厚度减小，坝体浸润线升高。当下卧阻水层厚度增大5 m、下卧导水层厚度减小5 m时，坝体浸润线升高0.16 m。

4.2 水力梯度变化

图3分别展示了均质粉质黏土坝基、粉质黏土厚5 m的层状土层坝基以及粉质黏土厚10 m的层状土层坝基的水力梯度的分布规律，其水力梯度最大值均位于坡脚处，小于临界水力梯度，故都不会发生渗透破坏。

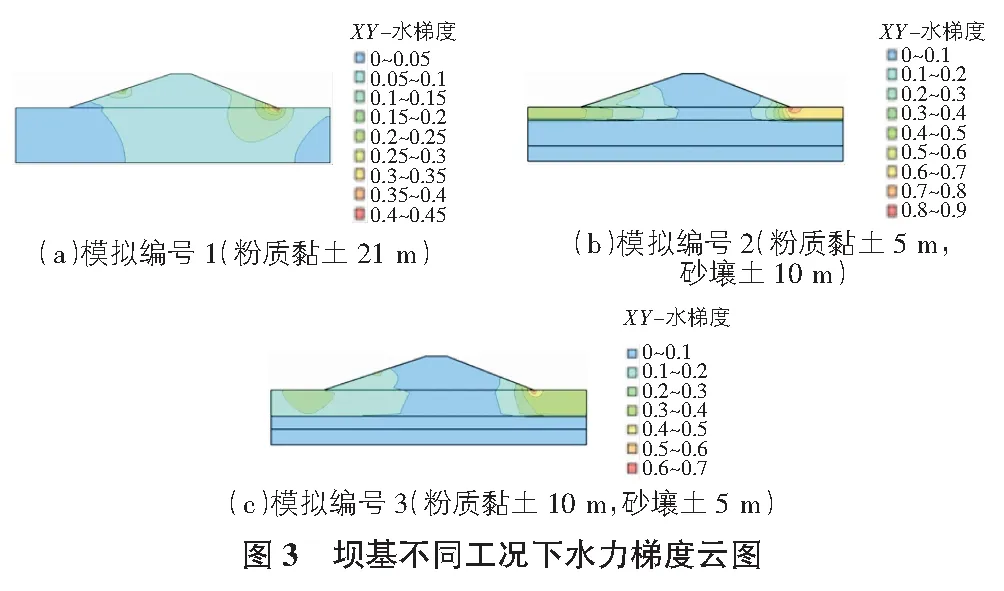
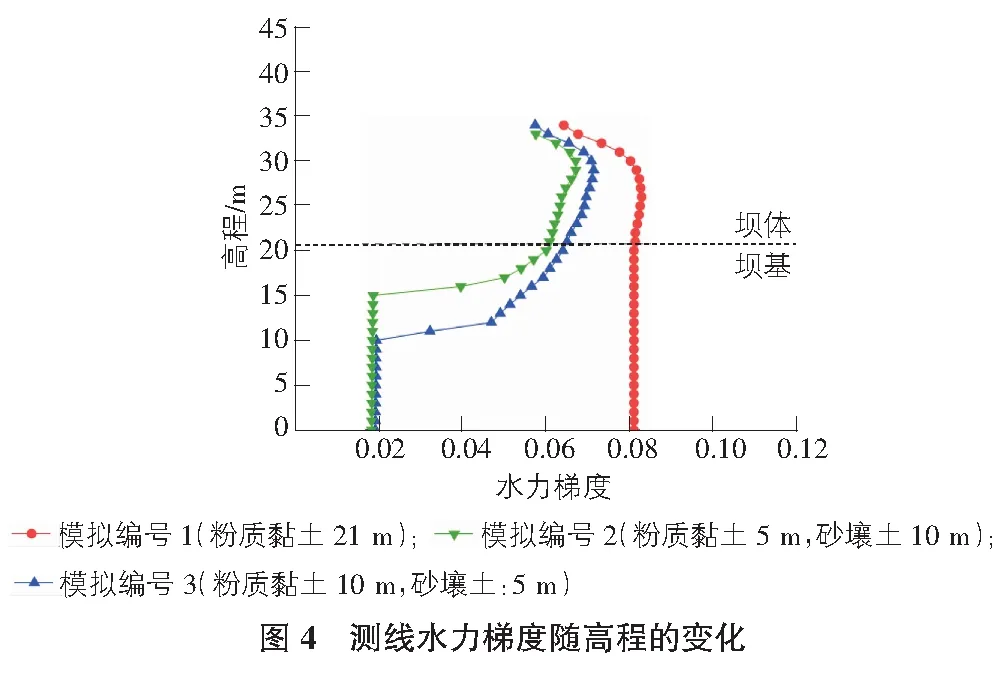
坝基不同工况下测线处水力梯度随高程的变化如图4所示，图4中虚线为高程21 m位置处，即坝体和坝基的分界线。均质土层、层状土层及其不同厚度的坝基，其水力梯度的分布有一定的差异。坝基不同工况下测线处的水力梯度均未超过各土层的临界水力梯度，均质粉质黏土坝基测线处最大水力梯度为0.083，层状土层坝基中，粉质黏土厚5 m的坝基，其测线处最大水力梯度为0.067 1，粉质黏土厚10 m的坝基测线处最大水力梯度为0.071 3。表明均质粉质黏土坝基测线处最大水力梯度最大，坝基较上层下卧阻水层厚度越大，水力梯度越大，当下卧阻水层厚度增大5 m时，测线处最大水力梯度增大6.3%。对于层状土层坝基，在坝体土层范围内，水力梯度随高程的增大呈现先增大后减小的趋势，具体表现为：坝基为粉质黏土厚10 m的水力梯度由0.065增大至0.071 3后逐渐降低至0.057 3；坝基为粉质黏土厚5 m的水力梯度由0.061增大至0.067 1后逐渐降低至0.057 5。在坝基土层范围内，层状土层坝基的水力梯度的变化趋势与均质土层坝基有所不同，其水力梯度的变化趋势呈现两段式，在坝基较下层即全风化砂岩和砂壤土层内水力梯度不变，而在坝基较上层下卧阻水层即粉质黏土层内，水力梯度随着高程的增大而增大，下卧阻水层厚度为5 m的坝基，其水力梯度增大了0.042 3，下卧阻水层厚度为10 m的坝基，其水力梯度增大了0.045 7，表明下卧阻水层厚度越大，水力梯度增大幅度越大。

4.3 流速变化

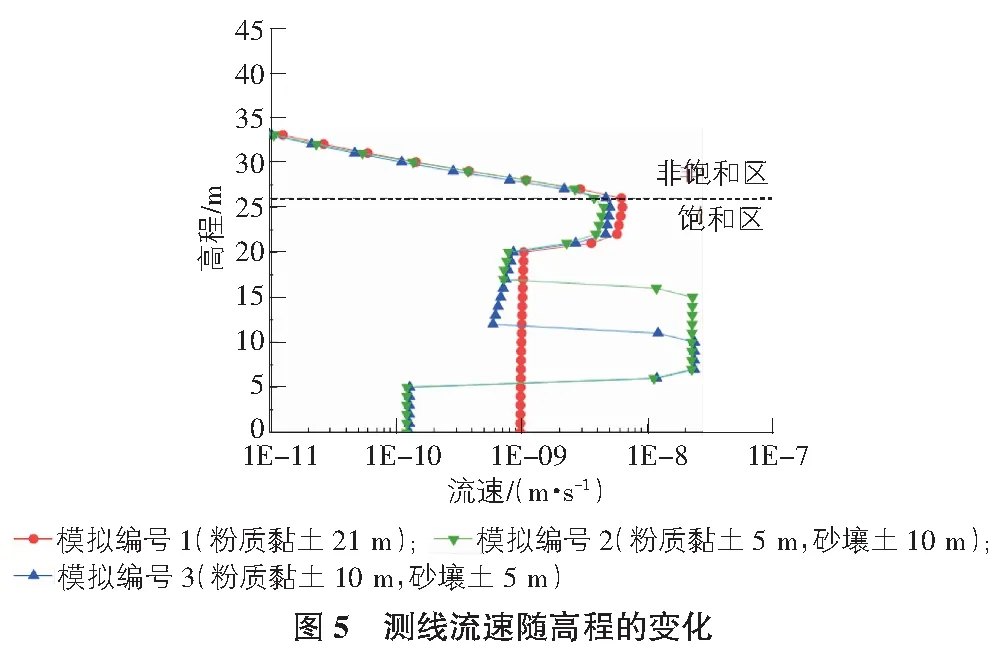
坝基不同工况下测线处流速随高程的变化如图5所示，图5中虚线为饱和区与非饱和区的分界线。对于层状土层坝基，在坝基较上层粉质黏土层内，土体渗透系数不变，由于水力梯度随高程的增大而增大，因而流速也随之增大。而在坝基较下层即砂壤土以及全风化砂岩土层内，水力梯度不变，渗透系数不变，水在各土层内的流速保持不变，但由于受到土层分层渗透系数发生变化的影响，在不同土层交界处流速会发生突变。具体表现为：对于粉质黏土厚10 m的层状土层坝基，在0 m～6 m,6 m～11 m饱和区域内，流速保持不变，在6 m处由于土层渗透系数变大，流速发生突变，在11 m～21 m粉质黏土层内，流速随水力梯度的增大而呈折线型上升，在21 m处由于土层渗透系数变大，流速发生突变。对于粉质黏土厚5 m的层状土层坝基，在0 m～6 m,6 m～16 m饱和区域内，流速保持不变，在16 m处由于土层渗透系数变大，流速发生突变，在16 m～21 m粉质黏土层内，流速随水力梯度的增大而呈折线型上升，在21 m处由于土层渗透系数变大，流速发生突变。对于不同厚度的层状土层坝基，坝基较上层粉质黏土厚10 m的流速略大于粉质黏土厚5 m的流速，表明坝基较上层下卧阻水层的厚度越厚，其测线处流速也越大，当下卧阻水层的厚度增大为10 m时，测线处最大流速为2.35e-8 m/s。

5 结论

本文根据饱和-非饱和渗流理论，开展二维有限元数值模拟，研究库水位不变条件下复杂地质二维大坝的坝体浸润线、水力梯度以及流速矢量的变化，同时将数值模拟结果与现场测压管水位数据进行比较，分析不同地质条件对坝坡稳定性的影响。主要结论如下：1)与均质土层坝基相比，层状土层坝基测线处的孔隙水压力值小3 kPa～4 kPa，浸润线高程降低0.3 m，上下游坝坡稳定安全系数分别提高了9.3%,10.9%；对于不同厚度的层状土层坝基，坝基较上层下卧阻水层厚度越厚，坝体浸润线越高，坝坡稳定性越差。当下卧阻水层厚度增大5 m、下卧导水层厚度减小5 m时，坝体浸润线高程升高0.16 m，上下游坝坡安全系数分别降低了6%,8.3%。2)在坝基土层范围内水力梯度有明显差异，具体层状坝基水力梯度的变化趋势呈现两段式，在坝基较下层水力梯度不变，在坝基较上层下卧阻水层内水力梯度随着高程的增大而增大，且下卧阻水层厚度越大，水力梯度增大幅度越大，当下卧阻水层厚度增大5 m时，测线处最大水力梯度增大6.3%。3)对于层状土层坝基，在坝基较上层粉质黏土层内，土体渗透系数不变，由于水力梯度随高程的增大而增大，因而流速也随之增大。在饱和区域内，流速的变化趋势主要受水力梯度及不同土层渗透系数的影响，当土层的渗透系数发生变化时，流速在土层交界处发生突变。对于不同厚度的层状土层坝基，坝基较上层下卧阻水层的厚度增大，其测线处流速也变大，当下卧阻水层的厚度增大为10 m时，测线处最大流速为2.35e-8 m/s。