爆炸波在复合钢板衬砌结构中的传播规律研究★
赵 越,刘 晓,李庆洲,赵明凯,宋 城
(1.兰陵县公共住房经营有限公司,山东 兰陵 277700;2.民航机场智能建造与工业化工程技术研究中心,天津 300456;3.民航机场建设工程有限公司,天津 300456;4.山东科技大学土木工程与建筑学院,山东 青岛 266590)
随着我国的城市化进程不断加快,交通拥堵问题日益显著,地铁作为一种便捷的交通方式,凭借其节约地面空间、噪声小、污染小的优点在全国范围内得到了大力推广。地铁隧道的发展加快了出行速度,有效地满足了城市交通需求,但也极易成为恐怖分子实行爆炸袭击活动的重点目标,存在一定的安全隐患。其中,复合钢板可以作为一种衬砌防护结构,能够吸收爆炸冲击波带来的能量,并且具有较高的抗剪强度,在地铁区间隧道的抗爆防护方面具有很高的适用性。因此,研究爆炸冲击波在复合钢板衬砌结构中的传播规律,在减少恐怖爆炸活动造成的财产损失和人员伤亡等方面有着重要的研究价值[1-3]。
要对地铁隧道实行合理有效的防护措施,了解爆炸冲击波[4]在隧道中的传播规律是保证地铁隧道安全运行的关键。与地上空间相比,地铁隧道区间是一个相对的“封闭系统”,炸药在地铁隧道区间中爆炸产生的空气冲击波会在封闭空间内部不断地传播和反射,其传播规律相比于传统空气冲击波而言更加复杂[5-6]。目前,有关爆炸荷载在地铁隧道中的冲击反应研究主要可以分为试验方法和数值方法。张玉磊等[7]使用不同药量的TNT开展了静爆实验,研究了不同装药量级TNT产生的爆炸冲击波在空气中的传播规律。爆炸试验非常昂贵,试验的可控性差,并且具有一定的风险性。因此,为弥补试验方法的不足,数值模拟方法得到了快速发展。
SMITH等[8]分别采用模型试验和数值模拟的方法研究了地下封闭空间内部产生的爆炸冲击波对衬砌结构的影响规律。孔德森等[9]基于实际的工程地质条件,采用流固耦合算法研究了爆炸冲击波对地铁区间隧道的冲击反应。李世强等[10]采用有限元软件AUTODYN研究了爆炸冲击波在某地铁车站内的传播规律和衰减规律,并得出了冲击波的杀伤范围。曲树盛等[11]采用Euler方法研究了爆炸冲击波在隧道区间的传播过程,得出了避免人员伤亡的安全距离,并分析了结构高度和出口距爆炸源的距离对冲击波传播的影响。GIANNOPOULOS等[12]采用激光扫描方法获取地铁车站及车厢的几何数据,使用EURO-PLEXUS程序的风险分析模块研究了不同装药量的TNT在地铁隧道区间爆炸后带来的损害。以上研究主要集中在爆炸冲击波在未设防护的地铁区间隧道的传播规律及杀伤范围。然而,目前有关爆炸冲击波在已设有复合材料防护的地铁区间隧道内的传播规律研究还不多见,研究成果也不够全面。
鉴于上述研究成果,基于流体动力学和爆炸学中的知识,本文提出了一种使用复合钢板作为衬砌结构的地铁防爆方法,建立了空气-炸药-复合钢板衬砌结构-周围土体的爆炸冲击模型。在地铁隧道区间使用复合钢板作为防护结构的条件下,研究了不同TNT炸药当量下爆炸冲击波的反射叠加效应和衰减规律,为地铁的抗爆防护设计提供参考依据。
1 数值模型的建立
1.1 复合钢板衬砌防护结构
复合钢板兼备金属材料和高分子材料的特性,被视为代替金属板的理想环保材料,具有防振和防噪声的优良性能。基于复合钢板的以上优良特性,将其应用于地铁隧道的防护领域[13]。复合钢板衬砌结构是由高强度聚酯纤维和两层钢板组成,其厚度比例为2∶1∶2,其中高强度聚酯纤维在两层钢板之间,采用焊接法制成。将其作为隧道的抗爆结构,具有良好的延展性和硬度,满足防护材料所需要的性能指标。复合钢板的结构特征见图1。

由于爆炸冲击波在地铁隧道区间的传播过程中呈现出非线性特征,使用双线性弹塑性本构模型[14]来描述复合钢板衬砌结构,使用Cowper-Symonds模型来描述复合钢板材料的应变率。因此,防护结构的动态屈服强度可以表达为:
(1)


表1 复合钢板衬砌结构的参数值
1.2 防护结构模型的建立
本文以南京市某地铁隧道工程为依托,使用动力学分析软件LS-DYNA建立复合钢板衬砌防护结构的数值模型。其数值模型结构简图如图2所示。
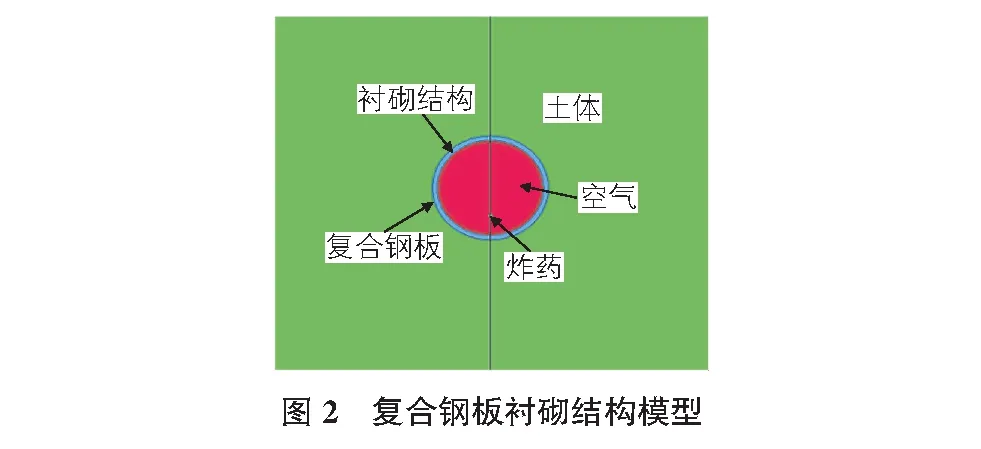
研究对象为圆筒形盾构隧道,埋深为15 m,外径为6.0 m,内径为5.4 m,复合钢板厚度为0.1 m,衬砌厚度为0.3 m。由于防护结构模型具有对称性,因此在建模计算过程中使用1/2模型。同时为减少边界效应,建立尺度为36×36×15的立方体结构作为整体的爆炸冲击模型,分别研究在10 kg TNT与30 kg TNT炸药当量下,爆炸源距离防护结构底部1.1 m处时产生的冲击效应。
1.3 炸药燃烧模型与参数
由于爆炸是瞬间发生的,因此可以忽略爆炸产生的冲击波在炸药和介质交界处之间的传播时间,只研究爆炸冲击波的外部传播规律[15]。炸药的爆炸参数列于表2。

表2 爆炸参数
TNT炸药产生的爆炸冲击效应可以使用JWL状态方程进行描述。爆炸产生的压力可以由单位体积的初始内能和相对体积来表达:
(2)
其中,P为压力;V为相对体积;E0为单位体积的初始内能;A,B,R1,R2,ω均为材料系数。基于LS-DYNA程序提供的“*EOS-JWL”关键字描述状态方程,将使用的具体参数值列于表3。

表3 JWL状态方程参数
整体结构中土体部分使用MAT-SOIL-AND-FOAM模型来描述。屈服函数f可以表达为:
f=J2-(a0+a1p+a2p2)
(3)
土体的变形特征使用Drucker-Prager屈服准则来描述。因此,土体的内摩擦角φ和土的黏聚力c可以表示为:
(4)
(5)
2 数值模型的计算结果分析
2.1 隧道结构受到爆炸冲击的应力分布
由于爆炸产生的冲击波是在半封闭的地铁区间隧道内进行传播,防护结构的动力响应变得更加复杂。因此,只研究模型内部空气的相关力学特性。同时,爆炸产生的冲击波作用时间短、频率高,从零荷载到最大值荷载只需要几毫秒。此外,防护结构在冲击波作用下产生的应力应变行为与冲击波的作用速率呈正相关。因此,为了更有针对性地研究爆炸荷载峰值的破坏作用并节约计算时间,数值模型的爆炸时间取50 ms。10 kg TNT炸药作用下与30 kg TNT炸药作用下衬砌防护结构各时间点的应力变化特征如图3所示。

由图3可以看出,炸药爆炸产生的冲击波会以球形波阵的形式向外传播,30 kg TNT作用下产生的冲击波能量更大,影响范围更广。爆炸点距离隧道底部仅有1.1 m,因此,爆炸冲击波会率先作用于衬砌底部。随着冲击压力增大,爆炸作用下的反射波继续向更远的范围内传播,随着距离的增加,爆炸产生的冲击波压强逐渐降低。同时,冲击波会在地铁区间隧道内部产生多次反射,这种反射叠加作用使隧道的爆源截面上出现多次应力峰值,并减缓了冲击波强度的衰弱作用,冲击传播规律更为复杂。此外,爆炸发生初期,隧道底部的冲击波传播速度较快,顶部冲击波在经历反射叠加作用后,速度也会有一定程度的加快。
2.2 不同爆炸当量下的压力时程曲线
为研究地铁区间隧道在爆炸冲击波作用下的受力特性,实验时分别在爆炸截面上环形布置28个测点,各测点的截面布置如图4所示。

由图4可以看出,1号~5号测点与爆源炸药中心的距离为1.1 m;6号~9号测点与爆源炸药中心的距离为2.2 m;10号~12号测点与爆源炸药中心的距离为3.3 m;13号测点与爆源炸药中心的距离为4 m;14号测点与爆源炸药中心的距离为4.3 m;15号~28号测点距离爆源的直线距离为6 m,其位置与1号~14号测点相对应。
2.2.1 10 kg TNT爆炸当量下的压力时程曲线
研究装药量为10 kg TNT产生的爆炸冲击波在安装有复合钢板地铁区间隧道的影响特征,并通过压力时程曲线研究冲击波的传播规律。10 kg TNT药量作用下1号,6号,10号,14号测点的压力时程曲线如图5所示。

由图5可以看出,爆炸冲击波在隧道区间的传播过程中会产生反射叠加作用,在1号测点处产生最大压力,数值为1.56 MPa,随后迅速衰减。6号~9号测点中,在6号测点处产生最大压力,数值为0.62 MPa;10号~12号测点中,在10号测点处产生最大压力,数值为0.46 MPa。由此可知,爆炸发生时衬砌结构外侧受到较大的压力作用。由1号和14号测点的压力时程曲线可以看出:1号测点只出现一次应力峰值,14号测点处历经多次应力峰值。由于爆炸是瞬时发生的,冲击波的反射叠加时间非常短暂,因此在1号测点处只出现一个应力峰值,并且1号点的应力值要远大于其他同距离的4个测点。因爆炸冲击波在密闭空间内的反射叠加作用,14号测点处会出现多次应力峰值,这与实际情况是一致的。
下面研究距爆源6 m处截面上的15号~28号测点的压力时程曲线,10 kg TNT爆炸当量作用下爆源截面处15号,20号,24号,28号测点的压力时程曲线见图6。

由图6可以看出,在靠近爆源中心的测点只出现一次峰值,并且持续时间较短;在距离爆源中心超过一定距离后的测点则出现多个峰值。这是因为爆炸冲击波在传播过程中会出现多次的反射叠加作用,初始的传播方向开始发散,导致测点处出现多次峰值。经过多次的反射叠加作用,反射冲击波的传播时间随着反射次数的叠加而逐渐增长,同一直线上各测点的峰值也会随着冲击波传播距离的增加而呈现出逐渐减小的趋势。
2.2.2 30 kg TNT爆炸当量下的压力时程曲线
选取测点1号~28号研究30 kg TNT炸药当量下爆炸产生的冲击效应,爆源截面处1号,6号,10号,14号测点的压力时程曲线如图7所示。

由图7可以看出,爆炸冲击波发生反射叠加作用与10 kg TNT爆炸当量作用下的特征相似。爆炸冲击波的最大应力发生在1号测点,数值为7.28 MPa,随后迅速衰减;在6号~9号测点中,最大应力发生在6号测点,数值为1.9 MPa;10号~12号测点中,最大应力发生在10号测点,数值为1.7 MPa。由此可知,衬砌结构外侧受到的爆炸冲击作用更强。由图7中各测点的压力时程曲线可以看出,部分测点出现多次峰值,相邻测点的应力变化特征出现较大区别。
通过对比分析30 kg TNT与10 kg TNT炸药作用下不同测点的压力时程曲线可知:与爆源中心距离3 m的范围内出现最大应力,最大应力峰值与炸药量之间并不是简单的倍数关系。部分测点在爆炸冲击作用下出现多次应力峰值,并且二次反射波峰值要高于初次爆炸时的冲击波峰值。也就是说,这些测点位置处会受到更严重的二次破坏。图8为距离爆源6 m处截面上测点压力时程曲线。

由图8可以看出,30 kg TNT产生的冲击波在3 m~6 m距离范围内出现多次反射叠加,压力峰值持续出现,之后趋于稳定状态;当距离超过6 m后,压力值出现多个峰值,并且持续时间较长;同一距离的30 kg TNT与10 kg TNT各测点峰值增幅之间接近倍数关系。
由两种不同爆炸当量下的压力时程曲线可以看出:在距离爆源中心2.2 m的范围内,最大应力峰值出现在爆源中心线的底部位置,并且明显高于同距离测点的应力值;在距离爆源中心2.2 m~6 m的范围内,30 kg TNT与10 kg TNT爆炸当量下的压力时程曲线具有相似的变化特征,应力值随着时间的变化逐渐趋于平稳并且呈现出逐渐减弱的趋势;在距离爆源中心超过6 m的范围后,在第一峰值处并不一定会出现最大超压,不同测点处的应力特征也变得更为复杂。
2.3 爆炸产生的超压冲击
超压准则是指当爆炸冲击波产生的超压达到或超过一定值后便会对结构造成一定的伤害甚至破坏。目前主要通过爆炸-冲量准则、冲量准则和超压准则等方法来衡量发生的破坏作用。由于超压准则较为直观,因此,隧道结构在受到爆炸冲击时产生的动力响应可以用超压准则来分析。选用亨里奇公式计算超压峰值,将理论值与数值模拟结果进行对比分析,10 kg TNT与30 kg TNT炸药作用下的超压冲击结果分别列于表4,表5。
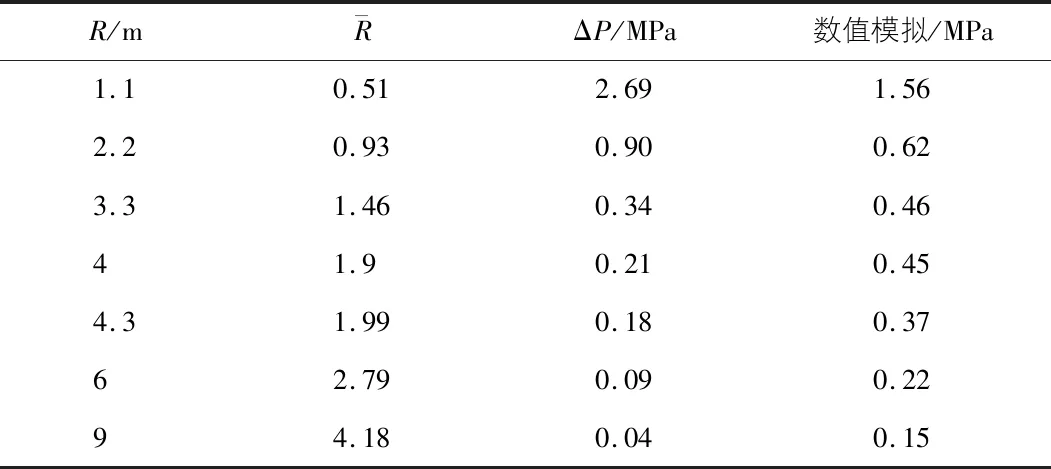
表4 10 kg TNT爆炸作用下超压峰值
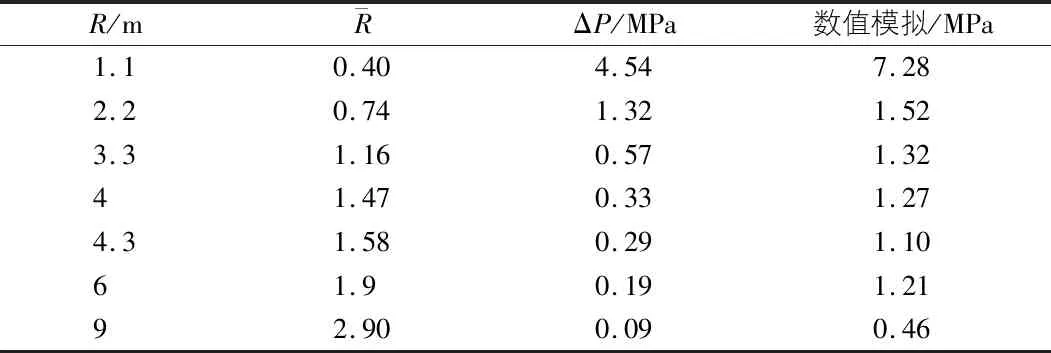
表5 30 kg TNT爆炸作用下超压峰值
由表4,表5给出的压力差值可以看出:数值模拟结果与理论计算结果并不是完全吻合的。在10 kg TNT炸药当量下产生的压力峰值的模拟值在距离爆源中心较近的范围内要小于理论值。随着距离的增加,模拟值与理论值的差值逐渐减小,并且当距离增大到一定程度后模拟值逐渐大于理论值;在30 kg TNT炸药当量下产生的压力峰值在距离爆源中心较近的范围内要大于理论值。两种计算方式得出的压力差值随着距离的增大而逐渐减小。在10 kg TNT和30 kg TNT炸药当量下,应力峰值在距离爆源中心2.2 m之外的范围内逐渐趋于稳定状态并且呈现出明显的减弱趋势,这符合爆炸波在隧道区间内传播的基本特征。
3 结论
1)爆炸冲击波在地铁区间隧道的传播过程中会出现复杂的反射叠加作用,由于爆炸冲击波的作用,衬砌结构底部出现最大压力,衬砌结构外侧相对于衬砌内部受到较大的压力作用。部分测点受到冲击波的反射叠加作用而出现多次应力峰值。2)爆源中心截面处的复合钢板衬砌结构受到最大的破坏作用。30 kg TNT炸药当量下爆炸冲击波的影响范围更大,使衬砌结构发生显著的塑性形变,应力峰值随着距离增加而呈现出逐渐减小的趋势。3)相同测点的应力峰值随着传播距离的减小得到一定程度的增大;10 kg TNT和30 kg TNT炸药当量下产生的应力峰值分别从1.4 MPa和6.5 MPa增加至1.55 MPa和7.28 MPa;不同测点的应力值随着时间的推进开始减小并逐渐趋于平稳,这符合爆炸冲击波传播的基本规律。