基于遗传算法的智能公交调度系统的研究
李清逸 李文娟 谢 鹏 刘向东 闫利霞
(苏州城市学院,江苏 苏州 215000)
随着我国国力的不断增强,国民经济飞速发展,城市化建设也得到不断推进,城市人口逐渐上升,公共交通和私家车成为城市居民的出行主要工具,私家车数量的增加造成了较为严重的空气污染和交通拥堵,不断增长的城市人口为公共交通带来了巨大压力。科学规划交通,合理调度资源,建设现代化的城市智能交通调度系统迫在眉睫。
智能公交调度系统在实际公共交通中的应用增多,许多学者针对出现的问题和不足采用不同的算法进行研究和改善。其中遗传算法、启发式算法、BP神经网络和其他智能优化算法对智能公交的调度优化方面有较大帮助。与其他优化算法相比,遗传算法的搜索从群体出发,在解决多辆公交调度的优化问题方面有较大优势。
1 智能公交调度系统现状
2021年智能公交领域进入发展冷却期,全国城市公交客流量大幅下降,但智能公交调度仍是城市公交发展的主要方向。随着智能公交调度系统的不断发展,一线城市与非一线城市的差距逐渐扩大。一线城市的发展趋于饱和,非一线城市的智能化基础设施完善程度有待提高、信息化基础较为薄弱、城市信息化设备老旧等因素为智能公交调度系统的发展带来巨大挑战。
在政策支持、技术进步、城市化进程和机动车保有量持续攀升等多重因素推动下,我国智能交通行业规模将稳步上升。综合政策规划和交通运输行业细分市场的发展状况,预计到2026年我国智能交通行业市场规模将突破4 000亿元,年均复合增长率在16%左右,智能公交系统的整体发展趋势稳步上升。2021~2026年中国智能交通行业市场规模预测如图1所示。
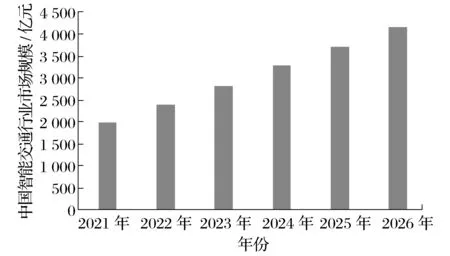
图1 2021~2026年中国智能交通行业市场规模预测
2 公交调度模型
公交调度指根据线路实时客流量情况,确定线路中各时间段发车次数及发车间隔,制成发车时间表,借此指挥城市公交的运营。
2.1 公交调度
公交调度分为动态调度和静态调度。动态调度指调度员在公交发车后,根据道路交通情况、车辆运行情况以及突发事件等其他实时信息,对公交的行车间隔等运营信息进行调整,保证公交车运行通畅,维持正常设定的服务水平。在动态调度中遗传算法应用较多,遗传算法能够较好地解决陷入局部最优解的问题。静态调度主要是确定线路上的车辆配比和发车计划,在满足客流需求的条件下,使城市公交的运营变得科学高效。静态调度是公交调度的基础,文章主要从静态调度入手,研究基于遗传算法的公交调度系统。
2.2 公交调度优化问题分析
调度的目的是合理规划资源分配,制定科学高效的行车计划,在运能供应充足和满足客流需求的条件下,提高行车速度和公里数,节约公司成本,公交调度的核心问题是保证乘客和公交公司的利益最大化。乘客利益方面,候车时间长短是乘客满意度的重要因素,如果要缩短乘客候车时长,需要增加运营的公交车数量,提高公交车到站频率。对公交公司而言,增加公交车运行数量,不符合经济利益,也为城市道路容量带来压力。公交公司利益方面,公交公司的收入要承担公交车的日常维护、折损、燃油和人员工资等问题。乘客利益与公交公司利益成对立状态,找出调度优化的平衡点是问题的关键。
2.3 模型建立
建立的目标函数包括乘客利益最大化,即乘客的平均等车时间最短;公交公司利益最大化,公司的发车次数最少。
目标函数如下:
式中:C1——乘客候车成本;σ1——乘客单位时间内的候车成本(元/min);a——站点;b——车辆数;C2——公司运营成本;σ2——一辆公交单位时间内的运营成本(元/min);ρ——a站的到站率;Tb,a——第b辆车到达a站的时间;tb,a——第b辆车离开a站的时间。
为了使目标函数满足乘客利益和公司利益的平衡,达到双目标优化的效果,需要分别对乘客候车成本和公交公司运营成本进行加权整合,加权系数分别为α、β,约束条件为最大发车间隔时间,文章选取为10 min,最小发车间隔时间为1 min,则目标函数为(其中min为函数的最小值,即目标函数C的结果为最小成本):
3 基于遗传算法的智能公交调度
静态公交车调度是多目标优化问题,遗传算法的搜索从群体出发,经过编码,选择,交叉,变异四个过程,能够快速找出问题的最佳解决方案。
3.1 基于遗传算法的公交调度模型求解
(1)编码。由于遗传算法不能直接处理问题空间的参数,必须通过编码将需要求解的问题表示成遗传空间的染色体或者个体[1]。系统采用浮点数编码中的实数编码较为简便,以公交的发车时间为变量,客流量峰值控制发车间隔。根据发车时段划分生成发车间隔,结合种群大小和一段时间内首末班车的发车时间和截止时间,完成初始种群选取。实数算法的优势在于种群的个体就是问题的解,不需要使用函数进行转换,且个体的优良基因段将会继续遗传到下一代,使得每一代都有进化。
(2)选择操作。选择操作是为了在群体中开展优胜劣汰。采用选择操作中的轮盘赌选择法和最佳个体保存法,使适应度值越好的个体被选择的概率越大。在遗传中每一代先保留一个最佳个体,且个体中不含重复的基因片段,按照选择概率划分区域将个体放入轮盘,然后对随机算子选中的个体进行配对。
(3)交叉操作。采用单点交叉可以得到更多合理的发车时间表。通过随机算子决定是否进行交叉操作,进行交叉的频率受设置的交叉率影响,个体在随机选择的位置点上进行交叉,得到两个新的个体,如果新个体中含重复片段,则重新选择交叉位点,直至新个体中不含重复的基因片段。
(4)变异操作。采用实数编码限制了变异基因的变异范围,不允许新个体中含有重复的基因片段。由随机算子决定是否进行变异操作,若进行编译操作,随机选择变异染色体的某个基因,将其转化为二进制编码后随机选择一位二进制位点进行变。如果变异后所选基因的值为0、1或者不在可变异区间内则重新进行变异。
3.2 算法的应用
(1)初始化变量。运算参数设定包括乘客的候车成本为1 元/min;公司运营成本为2 元/min,线路的站点总数为25个,线路的车辆总数为10辆,首班车时间为6:00,末班车的时间为21:00,发车次数为50次,平均运行时间为20 km/h。公交的到站率由每个站点的购票人数和发车间隔求出,将公交的发车时间到截止时间划分为几个时段区间,发车次数由预设定给出,具结合实际公交客流量数据样例。
(2)不同权重下最小成本的计算结果。模型中的权重取值代表利益中乘客利益和公交公司利益的占比大小,目标函数中权重的不同取值代表不同的最小成本,按照参数和苏州公交公司某条线路单日客流量数据进行计算得到不同权重下的计算结果,在α=0.5,β=0.5时(α+β=1)最小成本明显低于其他测试值。最小成本随α占比变化如图2所示。
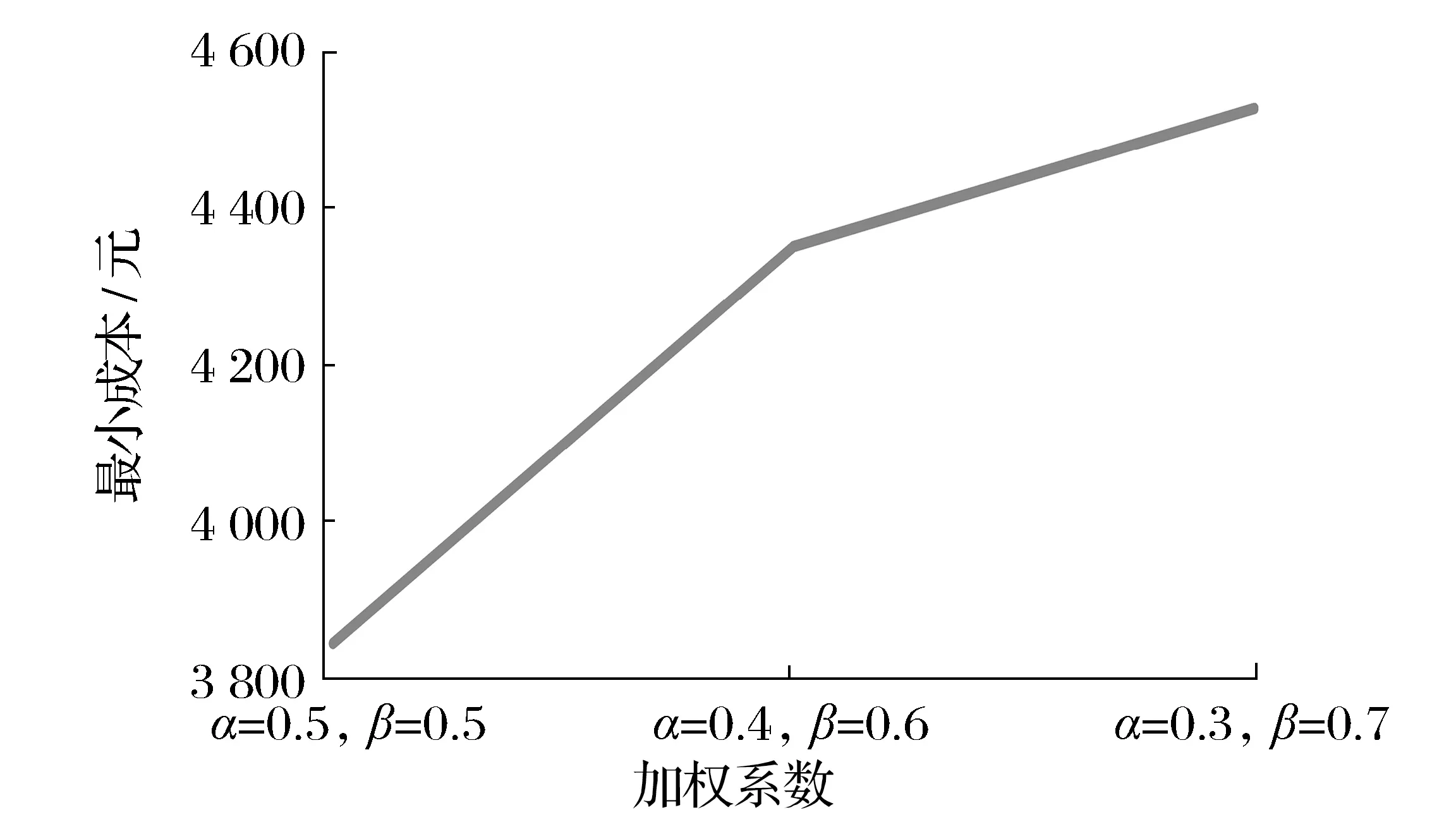
图2 最小成本随α占比变化
(3)不同交叉率、变异率、迭代次数下平均成本的计算结果。交叉率会对实验结果产生不同程度的影响,当交叉概率P1=0.7时,种群的平均成本较小,优于其他交叉概率下的测试值。
不同变异率对平均成本的影响较大,当变异概率P2=0.000 5时的平均成本优于其他测试值。
平均成本随迭代次数的增加而减小,当迭代次数n=400时的平均成本趋于稳定状态。
平均成本随交叉概率变化如图3所示。

图3 平均成本随交叉概率变化
平均成本随变异概率变化如图4所示。
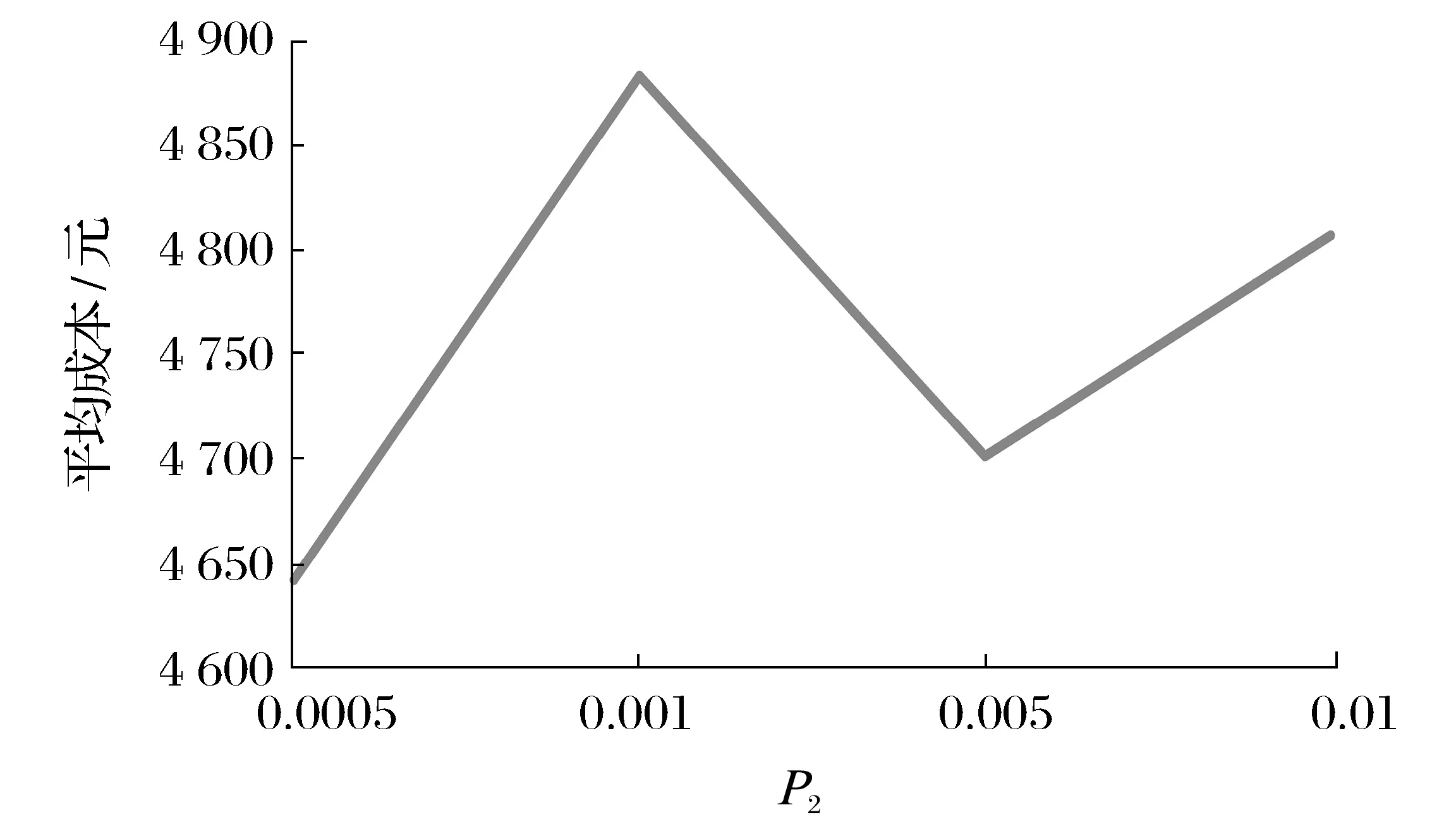
图4 平均成本随变异概率变化
平均成本随迭代次数变化如图5所示。
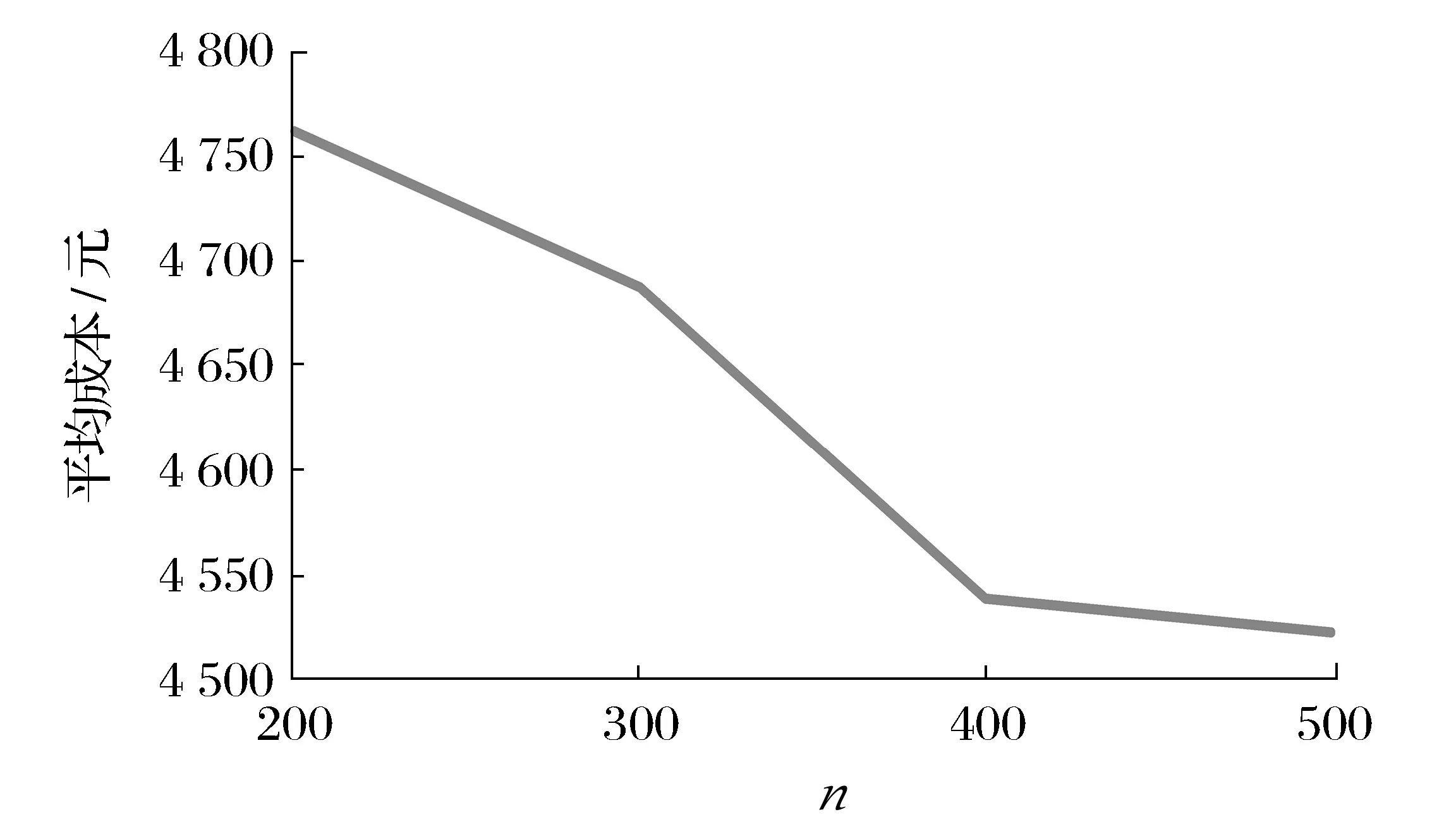
图5 平均成本随迭代次数变化
4 结语
随着时代的快速发展,解决城市交通拥堵的问题迫在眉睫,大力发展城市公交,优化城市公交调度系统能够有效解决交通拥堵问题,结合遗传算法、科学规划交通以及合理调度资源为城市公交的发展带来更多可能。在未来的实践中,应结合动态调度分析在各类异常情况下的调度决策问题,联合实际城市公交现状找到问题的更优解,形成更加成熟的现代化城市公交调度系统。

