钻孔数据空间插值方法的比较分析
孟宇豪
(苏州科技大学,江苏 苏州 215000)
钻孔数据作为地质勘察资料的重要信息之一,是地质建模、资源评价的原始数据来源,在建模和评价过程中起主要作用,是可以获得的第一手地下地质实物信息。目前,钻探工程已经被运用至多个领域,包括矿产资源的探查、地下水文、土层信息的勘察、工程基础的施工钻孔等,部分钻孔可将勘探与采集相结合,开采地下水、石油、天然气等资源。其数据分布的广度、密度、真实程度直接影响建模和评价结果的客观真实程度。但是,钻孔数据普遍存在离散分布、疏密不均的缺点,这就导致研究人员单纯依靠地勘资料直接提供的钻孔数据,难以创建较为精细、准确的三维地质模型,难以对地资源进行准确评价。利用插值方法对钻孔数据进行空间插值拟合,可以解决钻孔数据离散化、分布不均的缺点,为三维地质建模和地下资源评价提供可靠支撑。因此,对不同空间插值方法下的钻孔数据插值精度进行比较分析,可以提高插值结果的精确程度,对地质建模和地下资源评价具有重要意义。
1 空间插值方法
1.1 插值方法分类
目前,研究人员对空间插值方法的分类标准并未达成一致,不同种类的空间插值方法适用不同领域,需要对各类插值方法的特点进行分析比对,选择适合地层曲面的插值方法。插值方法分类标准包括整体空间插值法、局部空间插值法和边界内插法;确定性插值法和地统计学插值法;精确性插值法和近似性插值法。
整体性插值指用研究区范围内所有原始数据进行整体空间拟合,适合对具有大范围变化趋势的数据进行插值,插值区域内的所有原始数据对每个插值点都有影响,单个原始数据的变化也会影响整个区域最后的插值结果。实际情况下,地质体中地层往往具有短程变化趋势,单一的大范围变化描述并不适用。局部空间插值指将整体插值区域分成多个插值子区域,每个子区域之间互不影响,局部空间插值法的单个原始数据点只能对所在子区域内的插值数据产生影响,不会影响整个插值区域,相比整体插值,局部空间插值对空间内的短程变化趋势具有更好的表述。边界内插法只适用于区域变化,只发生在边界位置,区域内部则默认均匀不变,这与地层变化的情况不符,不做讨论。确定性插值指以研究区内部的已知数据或已知变化趋势为基础利用数学函数来预测其他区域预测点的数值。
地统计学插值法即指克里金插值法,克里金插值法的优点在于它不仅引用了数学函数还增添了统计学的相关理论。统计学理论的添加使得克里金插值法在插值过程中可以产生不确定的插值曲面,以此来测算预测值的误差大小,在地理信息相关的插值作业中,克里金插值法被广泛运用。
精确性插值指插值结果中保留原始数据的插值法,在空间几何上的表现为,插值所得的曲面通过所有原始数据点。近似性插值指插值结果中对原始数据不做强制保留,插值所得的曲面不一定通过原始数据点。适用于地层曲面的插值法类别主要有局部空间插值法、确定性插值法、地统计学插值法、精确性插值法。
1.2 插值方法对比
插值方法种类较多,有的插值方法较为简单,有的则较为复杂,如克里金插值法。各个插值方法在优缺点和适用情况上也有很大差异,同一个插值方法处理不同类型的数据,其插值结果的误差也有很大区别,甚至在同一片区域内,不同的地层之间的最优插值方法也会不同。选择适合研究区的插值方法,可以提高建模结果的精确性,降低建模难度。文章主要采用反距离加权插值法、径向基函数插值法以及克里金插值法对某地区钻孔数据进行插值研究[1]。
(1)反距离加权插值法。反距离加权插值法基于空间相近相似原理即彼此距离较近的事物要比彼此距离较远的事物更相似,是一种确定性插值法。反距离插值法的搜索邻域可以通过设定半径大小人为改变,这使得该插值法在短程变化趋势和全局变化趋势的表述上都有较好表现,但其插值后的曲面不够平滑,容易引起“鸭蛋效应”[2]。
反距离权重插值法的一个重要影响因素是反距离的幂值,不同的幂值会产生不同的插值结果,幂值的高低可以根据原始数据的空间相关性进行选择。幂值越高,越强调近点的影响力,所得到的插值曲面越不平滑,过高的幂值会导致插值结果出现区域化、分级化的现象,造成插值结果精度下降,幂值越低,越忽视近点的影响力,最终的插值曲面越平滑。
(2)径向基函数插值法。径向基函数插值法是一种确定性插值方法,即插值表面必须通过每一个测得的采样值。径向基函数插值法包括五种基函数,分别是薄板样条函数、张力样条函数、规则样条函数、高次曲面函数和反高次曲面函数。反距离权重法虽然也能对短程变化进行表述,但表述较为生硬,插值后的表面不够平滑,与地层上下表面的变化趋势不够吻合,相比于反距离加权插值法,径向基函数插值法插值后的区域表面更加平滑,更加贴合地层上下表面的变化[3]。
(3)克里金插值法。克里金插值法是20世纪50年代初南非矿业工程师D.G.KRIGE发明的一种空间插值法。与前两种插值方法相比加入了统计学的相关理论,不仅可以拟合出预测曲面,还可以对预测值的误差进行验证分析,但克里金插值法的计算量较大,插值过程耗时较长,对数据的分布要求较高[4]。
1.3 插值选取流程
文章采用逐层对比择优的方法进行最优插值方案选择,操作流程:用反距离加权插值法、径向基函数插值法、克里金插值法分别对研究区内的9层土层进行插值拟合;针对不同的插值方法选取不同的插值参数,得出三种插值法的各土层插值结果;利用交叉验证的方式,计算各类插值方法的平均绝对误差和均方根误差;对比分析,选择最适合研究区土层的插值方法;利用验证指标的变化趋势对比图以及钻孔数据的预测值和实测值数值关系图检验选取结果的客观性。
2 插值过程及验证方法
2.1 插值过程
文章借助Arcgis软件中的Arcmap对研究区地层进行空间插值的研究,插值流程:在Arcmap中导入离散点坐标,生成离散点分布图;使用地统计分析模板选择插值方法以及插值单位;根据不同的插值方法设定不同参数;得到插值结果,分析误差。钻孔离散点分布如图1所示。
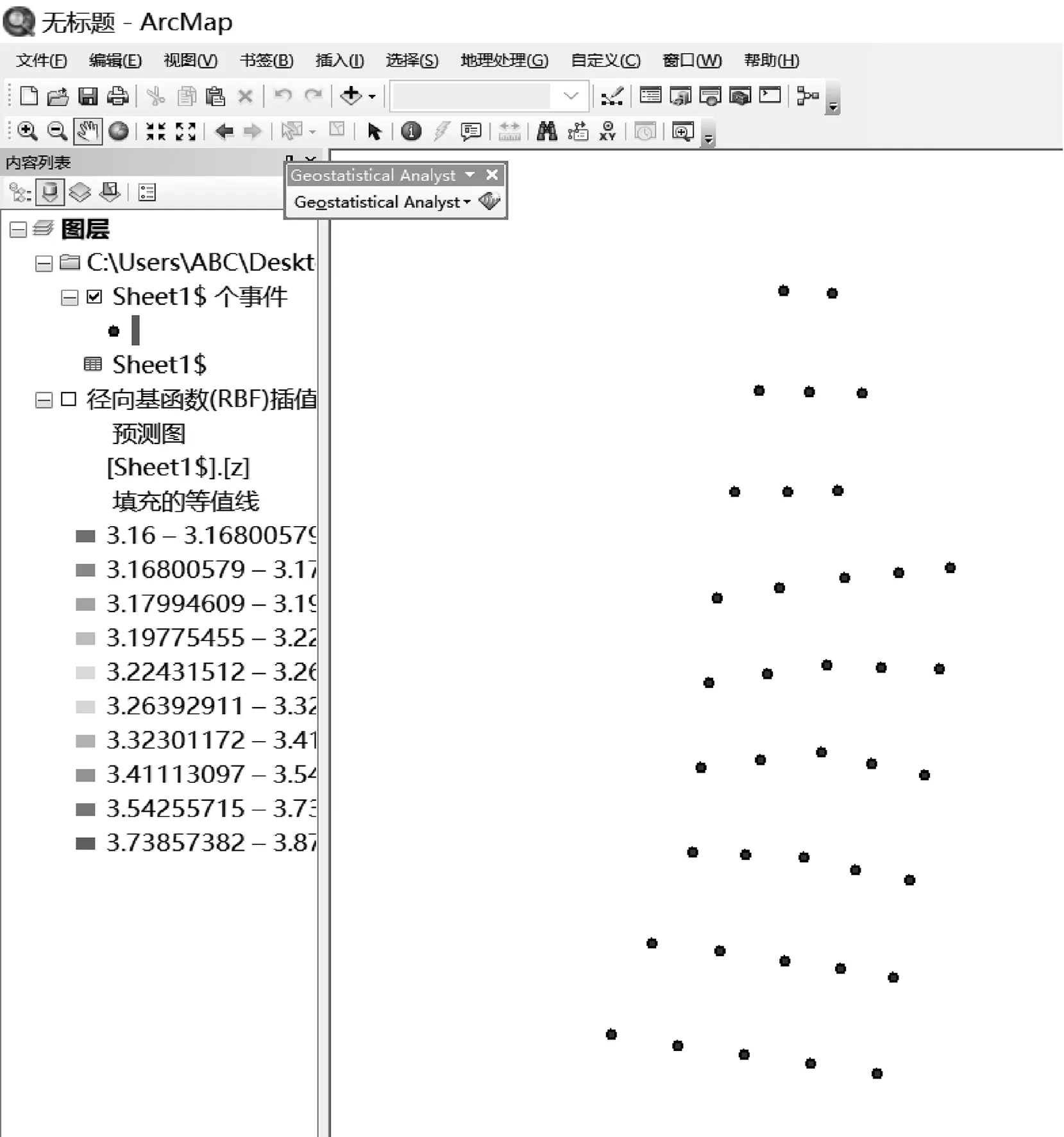
图1 钻孔离散点分布
2.2 验证方法
针对插值结果的误差验证可以将结果的精确性进行量化比较,从而选择最合适、误差最小的插值方法进行插值拟合[5]。文章采用交叉验证的方式进行插值结果的误差验证。交叉验证指的是从获取的数据内随机抽选一个点,将其层面标高当作检验样本。在剩余的钻孔点中运用插值方法计算该点数值,将估计值和原始值进行对比,得到检验样本误差。将该点放到初始数据内,重新抽取一个检验样本点,并选取其他的点开展插值估计,依次替换剩余样本。
验证指标包括(MAE)平均绝对误差(式1)、(RMSE)均方根误差(式2)。
式中:M——建模插值结果;N——验证样本数据;n——验证样本数。
3 结果与分析
研究区位于苏州市平江区皮市街以东,观成巷以南,旧学前以北,牛角浜以西。场地大部分原有建筑已拆除,地表多为建筑垃圾,因填土内建筑垃圾及原有建筑的水泥地坪及基础等障碍物影响,局部勘探孔稍做移位。研究区内场地地势平坦,地面标高在3.16~3.87 m。由于构造作用,地质体内部小范围存在地层尖灭等复杂情况,但总体呈连续成层分布。
研究区共有概化为9个土层,分别为填土、黏土、粉质黏土、粉土、粉土夹粉砂、粉质黏土夹黏土、粉砂、粉质黏土夹砂土、砂土,对上述9个土层分别进行三种插值方法的插值拟合,对插值结果进行交叉验证,选取各个土层最适合的插值方法,最优插值结果汇总如表1所示。
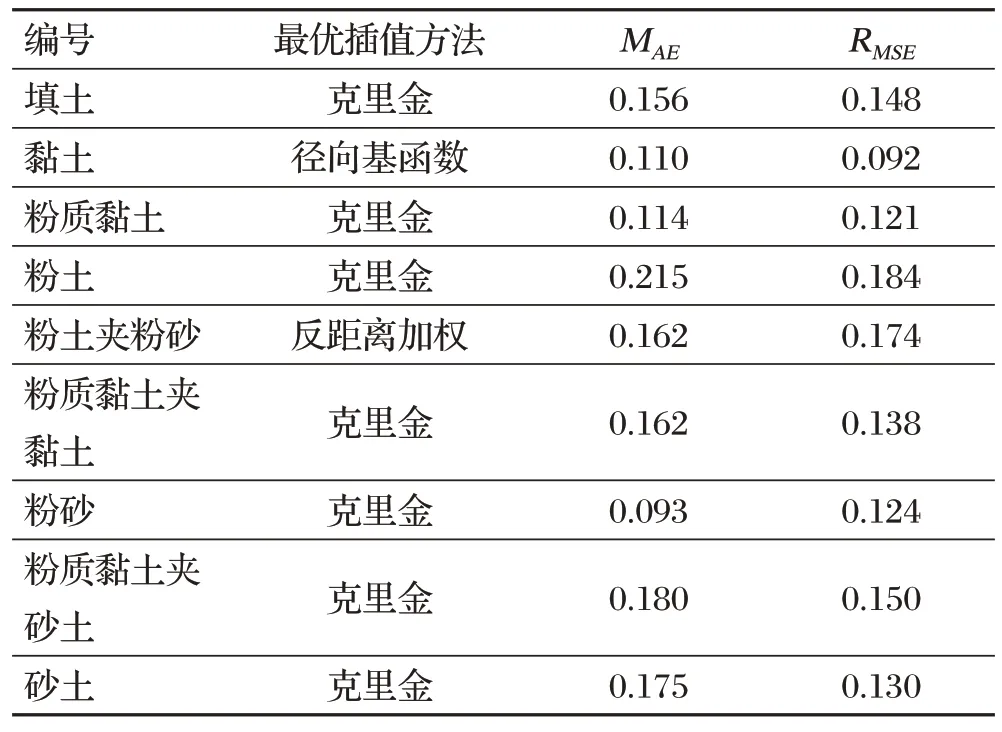
表1 最优插值结果汇总
从表1可以得到,除第2和第5土层,其他土层的最优插值方法均为克里金插值法,第7层精度最高,第4层粉土层精度最低,由于各个钻孔的粉土层埋深变化幅度更大导致实测值与预测值的差值较大,与实际情况相符,研究区钻孔数据的最优插值法为克里金插值法。
为了进一步验证选取结果的客观性,绘制各土层最优插值结果的MAE、RMSE值的变化折线图。可以发现MAE、RMSE两种验证指标的变化趋势基本一致,符合实际,侧面印证了文章采用的交叉验证方法能够较为准确地选择出各地层的最优插值方案。
粉土层实测值与预测值数值关系如图2所示。最优插值法MAE、RMSE值变化趋势如图3所示。
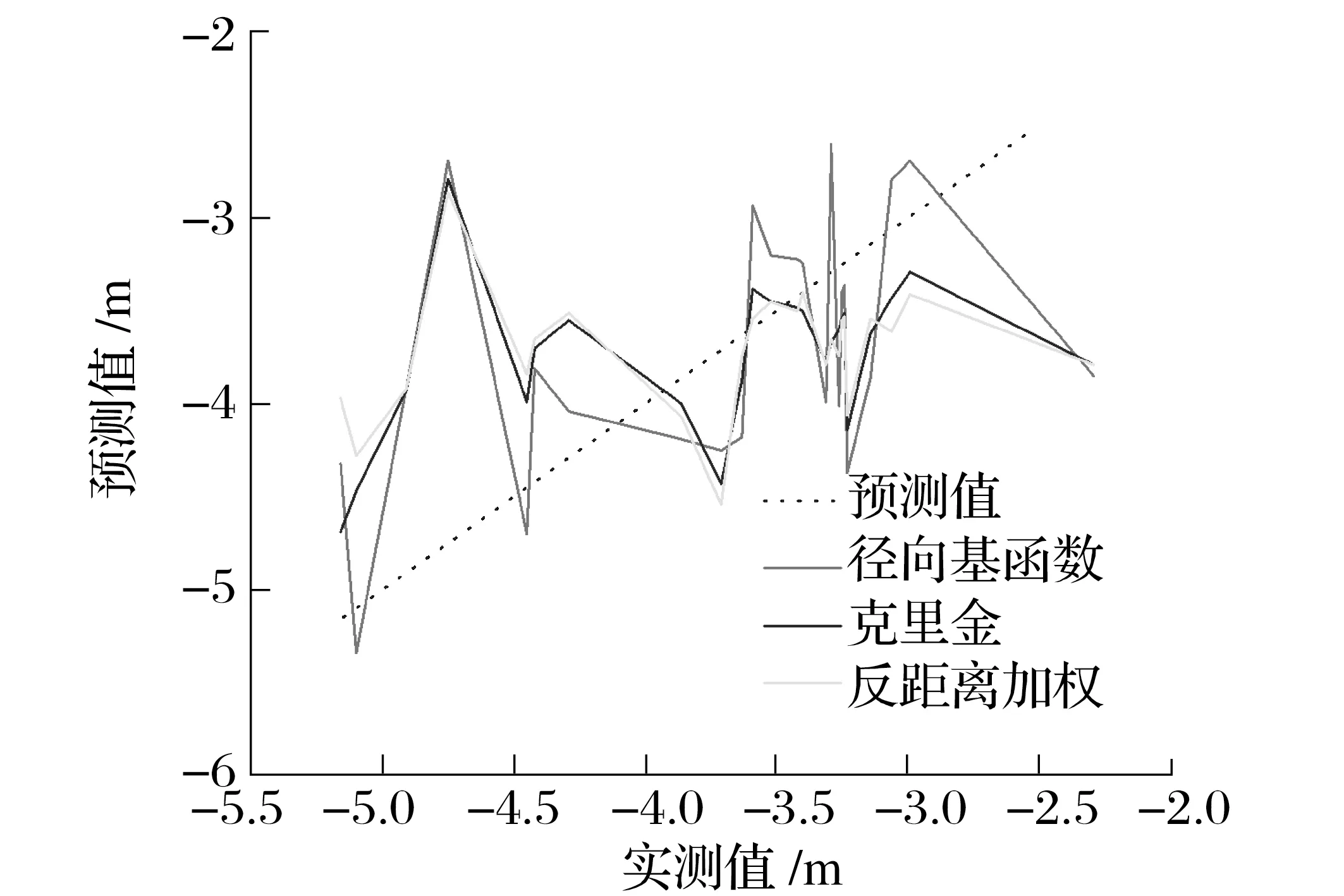
图2 粉土层实测值与预测值数值关系

图3 最优插值法MAE、RMSE值变化趋势
4 结语
文章基于Arcgis对某地区的钻孔数据进行插值拟合,利用交叉验证的方法从反距离加权插值法、径向基函数插值法、克里金插值法中选取最适合研究区的插值方法,并对结果进行分析验证,结果显示,研究区钻孔数据的最优插值方法为克里金插值法,粉土层的插值精度最低,粉砂层的插值精度最高。

