一种新型钢筋折弯机构的设计与仿真分析
周泽云,朱明清,曾广成,刘星伯,钟利萍
(1.中南林业科技大学机电工程学院,湖南长沙 410004;2.长沙智能机器人研究院有限公司,湖南长沙 410000;3.中交第二航务工程局有限公司,湖北武汉 430040)
0 前言
在建筑领域,钢筋部品的使用十分广泛。钢筋部品由钢筋网片组成,而钢筋网片由纵横交替的主筋与箍筋组成,网片之间用两端弯曲的拉钩筋固定[1-2]。
在建筑工地,传统的做法一般都是将拉钩筋先通过折弯机两端折弯后由人工放入网片内,再进行捆扎。由于是先折弯后放入,这就要求折弯后的拉钩筋要比网片间距略长,其结果会削减部分保护层,降低整个结构的强度。而将拉钩筋先放置在网片上再进行折弯可以最大程度地降低保护层的削减。
市面上常见的便携式钢筋折弯机采用电动机作为动力将钢筋直接拉入V形槽内完成弯曲动作。这样的设计不适合在钢筋网片上直接弯曲,因为产生的振动大、能耗高并且不符合当今智能化与节能低碳的要求。鉴于此,本文作者设计了一种新型的钢筋折弯机构,该机构可以作为建筑机器人的执行机构,实现将拉钩筋放入网片内然后折弯至最大135°的操作,并且拉钩筋不会凸出网片,提升了该工序的自动化与智能化水平及产品质量[3-5]。
1 几何建模
钢筋折弯机构如图1所示。根据折弯需求,采用最简单曲柄滑块机构即可达到目的。液压缸根据折弯精度需求也可改为电动推杆。在折弯过程中,为了减少机构对整个钢筋框架的振动,设计了半圆形的挡槽,该设计能保证弯折过程中产生的力不对外输出。使用时,将主筋与挡槽紧贴进行勾筋的定位,而勾筋则由夹持块固定,在弯杆的推动下勾筋被折弯到所需角度并始终紧贴主筋。
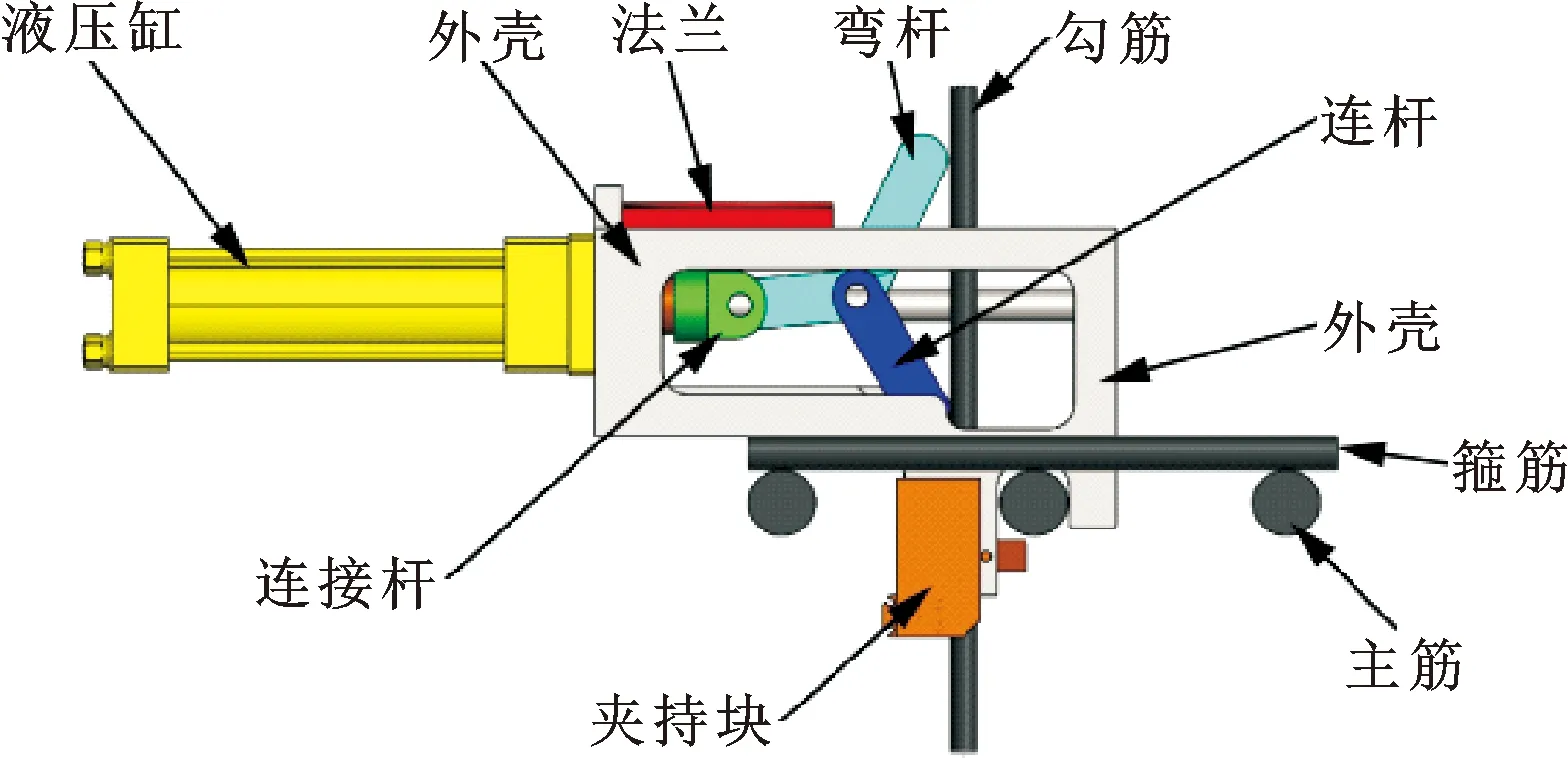
图1 钢筋折弯机构
该机构主要由夹持部分、折弯部分组成。夹持部分由上下两个气缸拉动夹紧块将钢筋夹紧,避免钢筋的滑动。折弯部分是由弯杆、连杆、液压杆、连接块组成的曲柄滑块机构。机构工作时由弯杆将钢筋折弯到最大135°。
2 数学分析
2.1 机构简化
折弯部分可以简化为曲柄滑块机构对其进行运动学与动力学分析[6]。钢筋折弯动作简图见图2。

图2 折弯动作简图
以点D为转动点的DE代表钢筋,A为液压杆,B为支点,E为钢筋DE与折弯机构的接触点。杆件AC、CB、AO、CE、ED、OB的长度分别为a、b、d、f、g、x,其中x为变量其余均为常数。α、β、ρ、λ分别代表杆AC、CB、CE、ED从水平方向沿着逆时针转动的角位移。
2.2 运动学分析
2.2.1 位置分析
运动学分析的目的是得到机构运动过程中的位置、速度、加速度,以此判断机构是否干涉、能否满足工作需求以及确定运动空间。为了得到较为精确的结果,采用复数分析法进行机构运动学分析。
构建封闭矢量方程式:
OA+AC=OB+BC
(1)
将式(1)改写为复数形式:
id+aeiα=x+beiβ
(2)
按欧拉公式展开:
id+a(cosα+isinα)=x+b(cosβ+isinβ)
(3)
该方程实部与虚部相等可得:
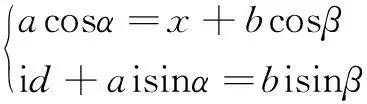
(4)
计算得出:
(5)
2.2.2 角速度分析
将式(2)对时间求导可得:
iaω1eiα=vx+ibω2eiβ
(6)
将实部与虚部分开列出方程组可解得:
(7)
式中:ω1为α的角速度;ω2为β的角速度;vx为杆A的水平运动速度。
2.2.3 角加速度分析
将式(6)对时间求导可得:
(8)
将实部与虚部分开列出方程组可解得:
(9)
式中:ε1为α的角加速度;ε2为β的角加速度;εx为杆A的水平加速度。
2.3 动力学分析
由于工作时反力的大小与方向都在随着x的变化而变化,故先计算出力的变化规律。在封闭的矢量多边形BDEC中建立矢量方程:
beiβ+feiρ=c+geiλ
(10)
将实部与虚部分开列出方程组可解得:
g2=b2+f2+c2-2bfcos(α-β-γ)-2bccosβ+2fccos(α-γ)
(11)
根据经验公式[7-8]:
(12)
式中:M为弯曲钢筋所需弯矩;K1为形状系数;K2为相对强化系数;K3为钢筋抗弯曲截面模数;r为钢筋半径;g为弯曲半径;σs为屈服强度。
设杆件2的质心为G2,BG2的水平距离为P12x,竖直距离为P12y,CG2的水平距离为P23x,竖直距离为P23y。同理可得到杆3的质心为G3,杆4的质心G4以及CG4的水平距离P34x、竖直距离P34y。质心位置如图3所示。

图3 质心位置
为了得到能与工作阻力Fg平衡的主动力F,可以采用动态静力分析法对整个机构进行分析,即通过达朗贝尔原理引入惯性力作为假想力进行静力分析[9-10]。各活动杆件的受力分析如图4所示。机构有3个活动杆件便可列出3个方程组,共8个方程、8个未知数。

图4 各活动杆件受力分析
(13)
(14)
(15)

将方程组改写成矩阵形式:
G·R=H
(16)
G=
矩阵G为系数矩阵,矩阵R为待求未知矩阵,而矩阵F则由惯性力、工作阻力、惯性力矩、阻力矩构成,求这些量所需要的质量、质心位置与质心加速度可以通过实际的模型与材料并结合运动学模型得出。
通过对机构的动力学分析,如:计算工作阻力、分析每个杆件的受力状况并运用动态静力分析法得到了机构的动力学模型,为机构的选材、液压缸的选型等提供了理论基础,并为类似机构的动力学分析提供参考。
3 仿真分析
文中的运动学与动力学仿真均基于ADAMS,通过对模型施加初速度和摩擦力来模拟实际使用情况,探究实际使用中整个机构的运动与受力并为有限元分析提供初始数据。
在a、b、d、f及γ分别等于70、80、63、90 mm及120°的条件下建立模型,设液压杆的初速度为0、加速度为20 mm/s2、末速度为20 mm/s,对杆ED施加力矩M代替钢筋给予机构的工作反力,并设置动摩擦因数为0.3对模型进行仿真。
以图2中点B为液压杆位移的原点,得到杆AC、CB、ED从水平方向沿逆时针转动的角位移α、β、λ与液压杆水平位移x关系,如图5所示。

图5 各杆的角位移与液压杆水平位移x关系曲线
杆ED的角位移λ从90°开始较为平缓地运动到 -45°,这代表钢筋的折弯角度从0°平缓地运动到135°,折弯过程中没有突变,这代表整个机构在运动中十分平滑,造成的振动较小。
由图6可知机构在不同运动姿态下的工作反力Fg与其方向τ的关系,为下一步有限元分析提供初始条件。通过液压缸出力F与其伸出长度x的关系能够准确判断出液压缸的负载均在设计承受范围内。
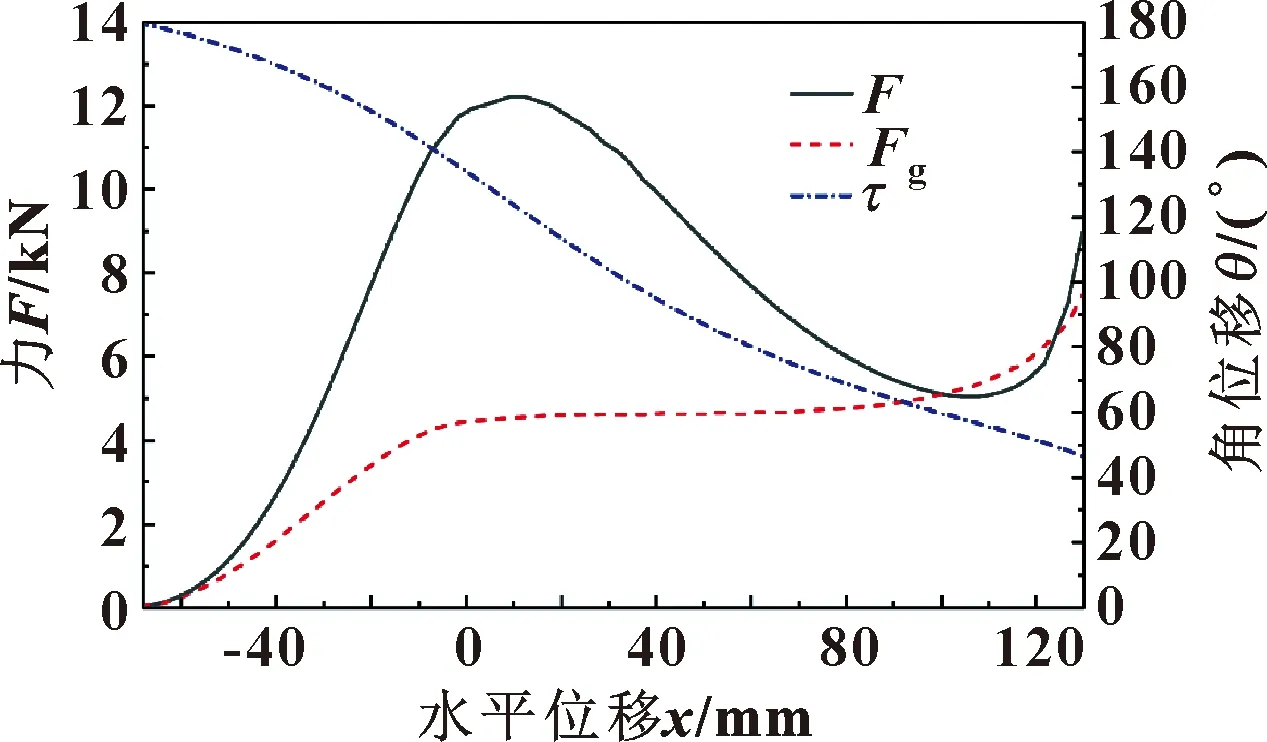
图6 液压杆出力F与工作反力Fg的大小与方向关系曲线
4 有限元仿真
4.1 仿真预处理
采用ANSYS软件的静态仿真模块进行有限元仿真。根据经验,材料选用45钢,其属性见表1。

表1 45钢材料属性
折弯机构受到钢筋给予的工作反力,作用在弯杆与钢筋的接触面上。根据ADAMS仿真结果,在钢筋被折弯到45°时对应着反力方向135°,大小4 430 N,钢筋被折弯90°时对应着反力方向90°,大小4 630 N,钢筋被折弯到135°时对应着反力方向45°,大小7 450 N。根据结果分别对弯杆端面施加反力,分别求出钢筋被折弯到45°、90°、135°时机构所受的应力与变形。
4.2 仿真结果与分析
仿真结果如图7—图9所示。结果表明:机构的最大位移在钢筋被折弯到45°时的接触处产生,最大值约为1.21 mm;机构所承受的最大应力在钢筋被折弯到145°时产生,最大应力为315.72 MPa,安全系数取1.1,45钢的许用应力为323 MPa,整个机构的强度满足要求。
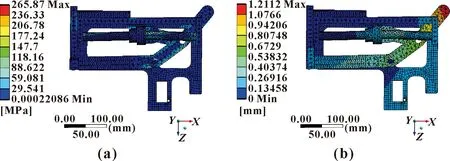
图7 钢筋被弯折到45°时弯折机构的

图8 钢筋被弯折到90°时弯折机构应力云图(a)与位移云图(b)

图9 钢筋被弯折到135°时弯折机构应力云图 (a)与位移云图 (b)
5 实物样机及试验
基于3D模型加工出了钢筋折弯机构实物,如图10所示。样机特性见表2。折弯部分采用电动推杆作为动力源,使运动更加精准;夹持部分采用气缸作为动力源,在满足要求的条件下降低了成本。经过弯折试验,机构能达到所设计的最大折弯角度,弯折成品如图11所示。

图10 钢筋弯折机构实物样机

表2 样机特性

图11 弯折成品展示
6 结论
对机构进行运动学与动力学的理论分析与计算,得到机构的运动范围及各杆件的受力情况,证明其在理论上是可行的。
对机构进行建模并基于ADAMS进行运动学与动力学仿真,模拟机构在实际工作中的状态与受力,并且为下一步的有限元分析提供机构在不同状态时的受力情况。
基于ANSYS对机构进行有限元分析,得到折弯机构将钢筋折弯至不同角度时的应力与位移云图,证明机构在各种运动状态下强度均是合格的。
根据3D模型加工出样机并进行弯折试验,达到了预期结果,验证之前理论计算与仿真的正确性,也为后续的改进提供参考。

