基于子空间重构的无监督时间序列异常检测

戈宁振，翁小清，袁子璇

（河北经贸大学信息技术学院，石家庄 050061）

0 引 言

时间序列是由一系列具有固定时间间隔的实值型样本组成的序列型数据［1］，广泛地存在于金融、工业制造以及医学等领域中。 当少量观测样本或由多个观测样本构成的序列显著地偏离大多数观测样本时，有理由怀疑这些观测样本是由不同机制产生的，这样的观测样本被认为是异常样本［2］。 时间序列异常检测就是在时间序列数据中找到这样的观测样本，为后续任务提供有价值的信息。 时间序列异常检测广泛地应用于工业生产监控［3］、金融风险预警［4］、医疗数据分析［5］以及网络入侵检测［6］等领域。

近几年来，基于深度学习的异常检测模型得到了广泛应用。 其中，基于重构的异常检测方法能够在复杂数据中提取特征信息，同时对噪声具有鲁棒性，受到了大量研究人员的关注。 例如Xu 等学者［6］利用变分自编码模型（variational autoencoder，VAE）检测服务器KPI 异常。 Yin 等学者［7］利用卷积神经网络构建的自编码模型（autoencoder，AE）检测物联网设备时间序列异常。 Zhou 等学者［8］利用对抗生成网络（generative adversarial networks，GAN）检测心跳时间序列异常。 基于重构的方法通过学习正常数据潜在的分布模式，假定不符合这些模式的异常数据难以重构，利用重构误差进行异常检测。 然而大多数基于重构的方法只假定正常数据服从单一模式，尤其对于子序列样本数据，忽略了多模式存在的可能。 如图1 所示，在MIT－BIH［9］心跳数据中，标记为正常的心跳样本存在多种波形，各个波形的形状差异较大，有理由认为这些波形遵循不同的模式。 如果不考虑数据中的多种模式，检测模型可能只会关注到单一模式，这必然导致遵循其他模式的心跳波形难以重构，造成大量的误判。

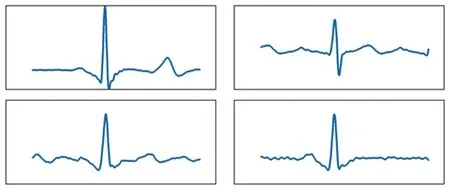
图1 4 个标记为正常的心跳波形，各个波形间存在显著差异Fig. 1 Four heartbeats are marked as normal and there are significant differences between them

针对上述问题，本文提出了一种基于子空间重构的异常检测算法（GMMSAE），旨在尽可能地学习时间序列数据中潜在的多种模式，以提高检测效果。GMMSAE 首先利用高斯混合模型（gaussian mixture model，GMM）在稀疏自编码（sparse autoencoder，SAE）的潜在变量上进行聚类，利用聚类结果将原始输入样本分割为不同的组，这样的组称其为子空间，每个子空间中的数据遵循特定的模式。 之后每个子空间训练对应的SAE 模型，以达到学习复杂数据中多种模式的目标。 在检测阶段，每个样本利用这些子空间模型进行重构，最小的重构误差作为样本异常得分，异常得分高于指定阈值的样本被认为是异常的。 本文在多个真实的时序数据集上进行了实验，结果表明：提出的方法在AUC（area under curve）和AP（average precision）两个性能指标上，显著地优于已有方法。

1 相关工作

在时间序列异常检测领域，早期时间序列检测模型主要基于统计学方法。 此类方法通过对时间序列历史数据进行建模，挖掘数据中蕴含的模式或规律对未来数据预测，利用预测误差识别异常数据。常见的方法有差分整合移动平均自回归模型（ autoregressive integrated moving average model，ARIMA）［10］、 隐马尔可夫模型（hidden markov model，HMM）［11］以及指数权重移动平均模型（exponentially weighted moving average，EWMA）［12］等。 基于统计模型的异常检测算法具有可解释性强、效率高等特点，但却无法捕获时间序列的非线性特征，难以适用于复杂的检测场景。

相比于基于统计学的检测算法，机器学习算法可以在不关注数据底层分布的情况下进行异常识别［13］，因此基于传统机器学习的异常检测模型具有更广泛的应用场景。 此类方法主要分为基于距离的方法、基于密度的方法、基于聚类的方法以及基于分类的方法［14］。 如Jones 等学者［15］通过定义范例样本（正常样本），计算其他样本与范例样本之间的距离定义异常分数，异常分数高的样本被认为是异常的。 但现实世界中的时间序列数据复杂多变，寻找一个能够同时考虑形状信息和尺度信息的距离度量是困难的。Breunig 等学者［16］将局部离群因子（local outlier factor，LOF）用于时间序列异常检测。 LOF 是一种基于密度的异常检测方法，通过密度估计的方式，将低密度区域的数据识别为异常。 基于密度的方法需要大量样本进行密度估计，对数据规模有一定要求。Thuy 等学者［17］利用Leader 聚类进行异常识别，将远离大多数类簇的样本识别为异常样本。 但在聚类算法中，类簇的数量难以确定，设定不合适会严重影响检测效果。 单类支持向量机（one－class SVM，OCSVM）［18－19］广泛地应用于基于分类的异常检测。 此类方法将异常检测转化为二分类问题，即正常样本属于一类，其他类别的样本都属于异常，通过寻找合适的分类边界将正常数据和异常数据进行区分，非常适用于类分布极度不平衡的数据。 但对于高维复杂的时间序列，分类边界很难找到。 总地来说，基于传统机器学习方法的检测模型在数据量较小、数据维数较低的情况下，能够获得较好的检测性能。 但随着时间序列数据日益庞大且复杂，这些方法难以提取有效特征，导致检测效果不理想。

近些年，随着深度神经网络的快速发展，大量基于深度神经网络模型的时间序列异常检测算法得到了应用，并取得了显著效果［20］。 如长短期记忆网络（long short－term memory，LSTM）［21］，该方法能够有效地捕获时间序列的时序依赖，非常适合时间序列建模。 Hundman 等学者［22］利用LSTM 作为预测器检测航天器时间序列中的异常，比传统算法的性能有显著提高。 相比于基于预测的异常检测，基于重构的深度学习模型具有更高的性能以及对噪音数据的更鲁棒，大多数研究者聚焦于基于重构的检测模型。 基于重构的异常检测模型尽可能地还原输入样本，利用重构样本与输入样本之间的误差进行异常检测。 如Thill 等学者［23］利用时序卷积自编码模型（temporal convolution network autoencoder，TCN －AE）检测心跳样本异常，该方法通过重构不同时间尺度的时序特征，以提高样本的重构准确度。 然而，TCN－AE 没有正则化，容易出现过拟合，导致检测精度降低。 针对此问题，Li 等学者［24］提出了一种基于平滑诱导的变分自编码器进行异常识别，该方法在损失函数中引入了扩展的Kullback－Leibler（KL）散度作为平滑度正则器惩罚非平滑的重建，使潜在空间的学习可以更加关注“正常”模式，而不是盲目地最小化原始信号和潜在变量生成的信号之间的重建误差，有效地避免了过拟合。 Siouda 等学者［25］提出SAE，从特征稀疏化角度避免了过拟合问题，在心跳样本异常检测中取得了理想的效果。 另外一类基于重构的异常检测方法是基于GAN 的，GAN 通过生成器和判别器之间的对抗训练生成高质量的重构特征。 例如，Zenati 等学者［26］基于双向GAN 构建异常检测模型，能够有效地减少训练时间并提高检测性能。 但此模型结构复杂，不适用于数据较少、维度较低的小数据集。 Zhou 等学者［8］提出了一种基于GAN 的心跳异常检测模型，通过重构心跳样本进行异常检测。 但此模型只适用于周期性数据，对于非常周期性的样本数据难以检测。 由于GAN 内在的结构问题，基于GAN 的方法往往难以训练，存在模式崩溃的问题［27］。

通过以上回顾可以看出，在复杂多变的时间序列数据中，已有基于AE 的重构检测方法容易过拟合，而基于GAN 的模型难以训练。 同时，这些方法在大多只考虑了数据服从单一的分布模式，忽略了存在多模式的可能。 因此，有必要构建一种简洁高效，同时能够全面地捕获潜在模式的检测模型。 因此，本文提出了一种基于子空间重构的无监督时间序列异常检测模型，通过高斯混合模型在SAE 的潜在空间中聚类，将输入样本划分为多个独立的子空间，并利用SAE 出色的特征学习能力来捕获多模式特征，以提高检测效果。 同时，本文提出的模型结构简单，训练效率高，具有很好的泛化能力。

2 本文方法原理与设计

本文提出的模型主要由SAE 和GMM 构成，本节将先分别介绍这2 种相关技术，之后描述整体模型以及模型的训练和异常检测。

2.1 稀疏自编码

AE 是一种基于无监督训练的神经网络结构，其目标是尽可能地将输出值还原为输入值，因此被广泛地应用于基于重构的异常检测。 传统的AE 模型聚焦于学习稠密的特征，容易出现过拟合问题。 相比于稠密特征，稀疏特征具有更强的表达能力，受稀疏编码的启发，SAE 通过在损失函数中添加稀疏惩罚项来学习样本中的稀疏特征。 稀疏惩罚项尽可能地抑制”激活”的神经元，使学习到的特征不仅仅是输入样本的重复。

给定时间序列x，假设在第jth隐藏层的神经元为nj（x），当nj（x）的输出值等于“1”时，意味着此神经元处于激活状态，否则，等于“0” 时，表示非激活状态。 在特征学习过程中，隐藏层神经元的激活值通过（1） 来计算：

其中，ω为权重矩阵，b为偏置。 因此，nj（x） 的平均激活值定义如式（2） 所示：

其中，m表示特征空间的维度。 因此当神经元的平均激活值远远大于期望值时，通过附加一个正则化项对其惩罚，能够使模型学习到的特征趋向于稀疏。 在SAE 中，稀疏正则项使用Kullback－Leibler散度来实现，如式（3）所示：

当训练稀疏自编码时，有可能通过增加权重值和减少隐藏神经元的值来降低稀疏正则化项的权重，因此SAE 通过增加一个L2 正则化项防止这种现象的发生，L2 的定义如公式（4） 所示：

其中，J表示隐藏层数量；L表示神经元数量；K表示训练样本数量。 SAE 最终的损失是一个经过调整后的均方误差，定义如式（5）所示：

其中，α为稀疏惩罚项系数，用来控制稀疏正则的权重，β为L2 权重正则的控制系数。

2.2 高斯混合模型

高斯混合模式是由K个分模型构造的概率模型，每个分模型服从正态分布。 通常情况下，给定时间序列x，其概率密度分布可以表示为：

更新参数需要计算第k个高斯分模型在当前参数下生成xi的概率tik，计算方式如式（8）所示：

模型参数更新如式（9）所示：

其中，Nk为第k个分模型所覆盖的样本数量。 EM中的E 步和M 通过交替的迭代，直到模型收敛。

2.3 模型架构

为了全面地学习时间序列中潜在的多种模式，本文结合SAE 和GMM 构造了基于重构的无监督异常检测模型，模型的总体结构如图2 所示。

图2 模型结构图Fig. 2 Model framework

由图2 可知，在训练阶段，模型首先利用SAE提取输入数据在潜在空间高级别的特征。 SAE 的基本结构包括一个编码器和一个解码器。 编码器将原始输入转换为潜在空间的低维表示，用z来表示。而解码器则尽可能地将z重构回原始空间。 一旦SAE 训练完成，就可以获得包含输入数据关键特征的隐藏表示z。

当输入数据的特征提取完成后，使用GMM 对隐藏表示z进行聚类，并根据聚类结果的索引将原始输入数据分成不同的组，每个组是一个独立的子空间，同一子空间的数据遵循相同的模式。 为了准确地学习每个子空间的样本特征，每个子空间训练一个独立的SAE，这些SAE 被称为子模型。 子模型的结构与上述SAE 的结构相同。 显然，对于给定数据，并不知道存在多少个子空间，而子空间越多，则需要训练更多子模型。 研究可知，每个子空间的样本数量远远小于原始样本数量，如此一来模型的训练时间将大大减少，同时这些子模型可以并行训练。因此，整个模型的训练时间并没有增加。

2.4 异常检测

本文提出的模型根据子模型重构误差识别异常样本。 样本的重构误差越大，则其为异常的概率就越高。 在本文的模型中，样本的异常得分是通过输入和重构之间的均方误差（Mean Square Error，MSE） 来计算的。 在检测步骤中，每个样本被所有子模型同时重构，因此一个样本会有多个重构误差。通常情况下，如果测试样本遵循某个子空间的模式，那么测试样本可以被其对应的子模型重构得很好，而其他子模型的重构误差自然较大。 因此，研究选择所有子模型中最小的重构误差为样本最终的异常得分，如公式（10）所示：

其中，Esubmodel－i表示第i个子模型对样本x的重构误差。 当样本的异常得分高于指定阈值时，该样本被认为是异常的。

3 实验

为了验证本文模型的有效性，本节分别进行了对比实验、消融实验、参数敏感实验以及可视化实验，从多个角度分析了基于子空间重构的异常检测模型的性能。

3.1 环境和数据集

实验模型基于Python 3.6 和Matlab 2022a 进行构建，硬件平台为Windows 10，CPU Inter Xeon（R）CPU E3－1231 v3@ 3.40 GHz，内存16 GB，GPU NVIDIA GTX1080ti。

本文在6 个数据集上进行了实验，这些数据集分别来自MIT－BIH 数据集和UCR 数据集，数据集详情描述如下：

（1）MIT－BIH 数据集［9］。 来源于Beth Isral 医院采集的48 个病人的心电图记录，并由2 名以上心脏病专家在每个心跳节拍的波峰位置标记出心跳类型。 根据AAMI（Association for the Advancement of Medical Instrumentation）［28］的建议，当心跳节拍被标记为N，L和R4 时表示正常，而其他类型为异常心跳。 由于部分记录的数据质量不够，102、103、107和218 的记录在该实验中被删除。 此数据集共包含2 860 万个数据点，共计97 568 个心跳节拍样本。为进行公平比较，本文采用文献［8］中的数据处理方式，将原始心跳记录分割为周期相同的心跳节拍样本进行异常检测。

（2）UCR 数据集［29］。 是时间序列异常领域重要的基准数据集，很多时间序列相关的算法使用了该数据集进行评估。 UCR 共包含128 个不同领域的数据集，本文从中选取了5 个数据集，包含不同的标签种类及特征长度，能够有效地反映检测算法的泛化能力。 所有数据集的统计信息见表1。

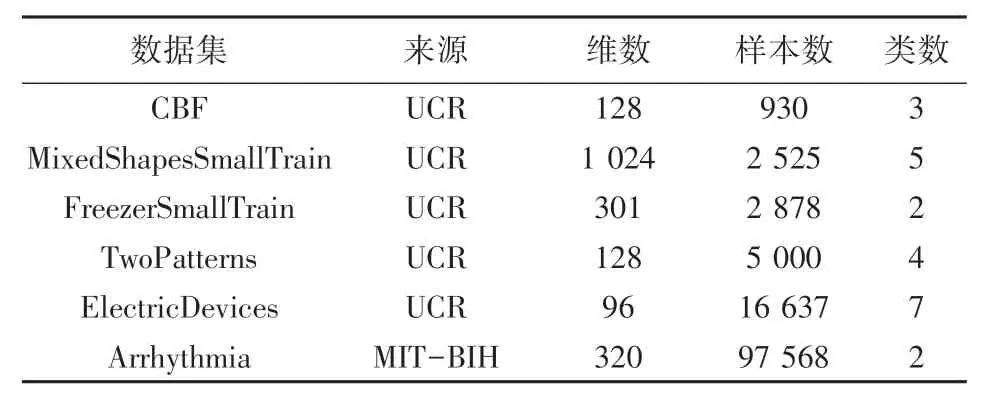
表1 数据集统计信息Tab. 1 Statistical information of datasets

3.2 评价指标

本文采用（Average Precision，AP） 和（Area Under Curve，AUC）评估模型性能。AP和AUC能够同时考虑模型对负类和正类样本的分类能力，在样本极度不平衡的状态下能够对分类模型做出公正的评估。

AP和AUC的计算涉及精确度（Precision）、召回率（Recall） 和假阳率（False Positive Rate，FPR），各个指标的计算方式如下：

其中，TP表示被预测为正类的正样本数量；FN表示预测为负类的正样本数量；FP表示预测为正类的负样本数量；TN表示预测为负类的负样本数量。因此，精确度表示预测为正类且实际为正类的样本占所有预测为正类的样本比例。 召回率表示被正确预测的正例占所有实际正例的比率。 假阳率表示被错误预测的正类占所有实际为负类的比率。 在此实验中，负类表示正常样本，正类表示异常样本。

AP的计算结果基于PR曲线（Precision Recall Curve），如图3 所示。 图3 中，横轴和纵轴分别为召回率和精确度，PR曲线与横轴及纵轴所围成的面积即为AP值。 召回率和精确度是此消彼长的，当模型能够平衡对异常样本的覆盖能力及检测精确度时，AP的值就会比较高。

图3 PR 曲线Fig. 3 PR curve

AUC的计算结果基于ROC曲线（Receiver Operating Characteristic Curve）。 与PR曲线类似，但该曲线是以假阳率为横轴，真阳率（召回率）为纵轴，ROC曲线与横轴及纵轴所围成的面积即为AUC值。 因此，当模型能够权衡对正类与负类的覆盖能力时，AUC的值就会比较高。

3.3 实验设置和参数

本文所有实验采用”One VS all”的方式进行模型训练，将所有数据集中的一类数据作为正常数据，其余类别的数据为异常数据。 为保证实验的公平性及可信性，按照文献［30］中的数据分割方式，将数据集中80%的样本作为训练样本，剩余20%作为测试样本。 此外，从训练集中采样25%的样本作为验证集进行参数调整，剩余训练集中所有正常样本参与模型训练。

本文模型存在一个重要参数，即子空间数量m，不同的数据集具有不同的m。 根据实验测试结果，各数据集最优实验结果对应的m见表2。

表2 数据集子空间数量Tab. 2 The subspace number of each dataset

模型常规的训练参数：训练轮数为200，学习率为0.000 1，L2 正则项权重系数为0.5，稀疏比率为0.05，稀疏正则项权重系数为1。

3.4 实验结果与分析

3.4.1 对比实验

为了验证本文模型的有效性，与5 个基准模型进行了性能对比实验，基准模型分别为AnoGAN［31］，ALAD［26］，Ganomaly［32］，BeatGAN［8］以及MMGAN［30］，实验结果见表3、表4 及表5。 其中，表3、表4 分别为AUC和AP的实验结果，表5 为单侧Wilcoxon 符号秩检验结果。

表3 AUC 实验结果Tab. 3 Experimental results of AUC

表4 AP 实验结果Tab. 4 Experimental results of AP

表5 单侧Wilcoxon 符合秩检验Tab. 5 One－sided Wilcoxon rank test

从表3 和表4 的指标平均结果（MeanAP，MeanAUC） 可知，GMMSAE 在所有数据集上取得了最优平均性能（MeanAUC0.946 6，MeanAP0.956 7），与平均性能表现紧随其后的MMGAN 相比，总体性能提高了 7. 0% （AUC），15.4%（AP）。 证明了GMMSAE 利用子空间重构能够充分提取复杂数据中的多种模式，使模型更好地适用于多种检测场景。

从表5 可以看出，GMMSAE 与AnoGAN、ALAD、Ganomaly、BeatGAN 以及MMGAN，在AUC和AP的单侧Wilcoxon 符号秩检验概率p值均小于0.05，说明GMMSAE 的检测性能显著地好于其他5 个基准模型。

从表3 和表4 可以看出，在5 个数据量较小的UCR 数据集上，GMMSAE 的检测效果提升明显，在AUC和AP这2 个指标上，相对于MMGAN 提高了8.3%和18.5%，证明了GMMSAE 在小数据量的应用场景下，能够充分利用现有的信息对多模式特征进行捕获。 另外，GMMSAE 在MIT－BIH 数据集上，相对于MMGAN，AUC和AP上分别提高了1.1%和1.9%，证明了AEGMM 在大数据量的应用场景下，同样能够高质量地提取多模式特征。 相对比UCR数据集，GMMSAE 在MIT－BIH 上的性能提升相对不显著，主要原因是MIT－BIH 的弱周期性导致各个心跳节拍样本在时序位置存在大量差异，而这些差异会严重影响模型的整体性能。

对各个基准模型进行分析。 AnoGAN 需要寻找输入空间与潜在空间的最佳映射进行异常检测，而对于复杂且高维的多模式数据，往往很难找到最佳映射。 同时AnoGAN 对训练数据的数据量要求较高，因此其在5 个数据量较小的UCR 数据集上检测效果不理想。 ALAD 利用双向GAN 进行异常检测，但结构复杂，同样在数据量较小的场景下效率较低。Ganomaly 本质上是基于图像设计的模型，而时间序列样本数据存在很少的空间特征信息，因此检测效果不佳。 BeatGAN 对周期性较强的数据集上检测效果较好，但对于非周期性数据，如Two－Patterns 和Electric－Devices 上的检测效果较差。 MMGAN 在频域空间中考虑了多模态特征，因此相比前几个基准模型，在各个数据集上的检测效果有明显提升。 但MMGAN 未考虑原始数据在时域下的多种模式，同时部分数据在频域下的特征较为混乱，例如5 个UCR 数据集，因此在这5 个数据集上检测效果低于GMMSAE。

通过以上分析可以发现，现有异常检测算法都存在各自的局限性，对数据的规模及周期有要求，并不能作为通用模型对时间序列异常进行高效检测。本文提出的模型无论在小数据量、还是在大数据量的场景下都取得了令人满意的检测效果，解决了传统方法的应用局限性。

3.4.2 消融实验

为了验证所提模型各部分的有效性，在ElectricDevices 数据集上进行了消融实验，2 个变种模型分别为：

（1） GMMSAE w／o（without） GMM。 在模型中只使用SAE，不使用子空间重构。

（2）GMMSAE。 本文的最终模型，即使用SAE作为重构模型，并结合了子空间重构策略。

各模型的实验结果见表6。

表6 ElectricDevices 数据集消融实验Tab. 6 Ablation results on ElectricDevices

从表6 中分析可得，相较于未使用子空间重构的模型，GMMSAE 在AUC和AP两个指标上分别提高了6%和18.74%，这证明了多模式提取能够帮助模型学习到更全面的特征，有效地提高检测效果。

3.4.3 参数敏感实验

为验证子空间数量m对模型性能的影响，还进行了参数敏感试验。 在图4 中，分别给出了AP和AUC在Two－Patterns 数据集上随m的变化情况。由图4 可知，当m从2 增加到4 时，AP和AUC存在明显提升。 当m处于5 到10 之间，AP和AUC性能出现比较剧烈的波动。 之后，一直到m ＝20，AP和AUC总体维持在一个稳定的区间。 可以分析得出，当数据中存在多种模式时，分割的子空间较少，模型不能够完全捕获这些模式，因此性能没有达到最优。而当子空间过多时，模型的性能没有明显地提升，说明过多的分割子空间并不会提升性能。 因此针对不同的数据，选择合适的子空间分割数量，才能使模型的性能达到最优。

图4 AP 和AUC 性能变化Fig. 4 The performance change of AP and AUC

3.4.4 数据可视化实验

为了进一步探索本文模型针对不同样本的重构情况，本节对多个属于不同模式的正常样本进行了重构可视化，另外也对多个不同类型的异常样本进行了可视化。 具体而言，选取了MIT－BIH 数据集中4 个正常样本进行可视化，这些样本的整体特征不同，可以认为各样本分别遵循不同模式，重构效果如图5 所示。 另外，选取了MIT－BIH 中4 个属于不同类型（S，V，F，Q） 的异常样本进行可视化，如图6 所示。

图5 不同模式正常样本的重构Fig. 5 The reconstruction of normal samples with different patterns

图6 异常样本的重构Fig. 6 The reconstruction of abnormal samples

由图5 可知，每个子图中蓝色曲线表示原始样本，黄色曲线表示重构后的样本。 通过观察，虽然4个样本整体的形状特征不同，但各个样本的重构效果很好，原始样本与重构样本之间的误差很小。 因此通过子空间重构，模型可以有效地学习到数据中潜在的多种模式，达到对多模式样本重构的目的。

由图6 可知，红色曲线表示原始异常样本，绿色曲线表示重构后的样本。 通过观察，对于类型不同的异常样本，重构后的样本与原始样本差异很大，证明了模型并没有过拟合异常样本。 另外观测发现，重构后的样本呈现多种模式，进一步证明了本文的模型能够充分学习到数据中潜在的多种模式。

综合以上所有的实验结果，性能对比实验证明了本文模型在AUC和AP两个指标上实现了显著提升；消融实验证明了本文提出的子空间重构策略的有效性；参数敏感性实验证明了，模型在合适的参数区间具有稳定性；可视化实验证明了，本文提出的模型能够很好地重构多模式样本，并且不会拟合异常样本。 可以得出结论：本文提出的方法不但在性能上具有优秀的表现，同时能够适用于多种检测场景。

4 结束语

本文提出一种基于子空间重构的时间序列异常检测模型。 该模型能够学习复杂时间序列数据中的多种模式，一定程度上提高了异常检测的准确性。在6 个数据集上进了实验，结果表示，模型的性能显著地好于已有的时间序列异常检测方法，证明了多模式学习可以充分利用已有信息提高异常检测的准确度。 但本文提出的模型需要针对不同数据集调整子空间的分割数量，这是一个耗时、且成本较高的过程。 因此，下一阶段将考虑参数自适应调整以期望本文提出的模型具有更高的实际应用价值。