基于PSO-SVM-RF的离心泵转子故障诊断研究
范传翰,宋礼威,刘厚林,董 亮,肖幸鑫,陈泽宇
(1.江苏大学流体机械工程技术研究中心,江苏 镇江 212000;2.中广核工程有限公司核电安全监控技术与装备国家重点实验室,广东 深圳 518172)
0 引 言
离心泵广泛应用于国民经济的各个领域。由于离心泵工作环境复杂,运行工况调节频繁从而导致离心泵发生故障的概率增大,造成效率降低,甚至会出现安全事故。转子是离心泵中的重要组件之一,机组在长期运行过程中容易导致转子发生故障。其中,转子不平衡、不对中故障最为常见[1]。近年来,随着计算机技术的进步,国内外学者利用不同的方法为不同设备的故障诊断提供了很多参考[2]。屈梁生[3]系统研究了全息谱技术所衍生各项技术及在各类机械故障诊断实践中的应用。Dong[4]等人将小波包分解(WPD)与主成分分析(PCA)和径向基函数(RBF)神经网络相结合,完成了对离心泵汽蚀状态进行检测,并取得了较好的结果。董明[5]等人利用典型故障气体的相对含量在高维空间的分布特性输入到SVM(支持向量机)中对变压器故障类型诊断。薛延刚[6]等人改进了SVM 模型并引入故障分类准确性判定因子对水电机组进行了智能诊断。张丽平[7]研究了PSO(粒子群)算法的基本结构、算法特点、改进方法、实现模式及应用等方面并将其引入到BP 神经网络中,取得了满意的结果。蔡振宇[8]等人将PSO-SVM(粒子群优化支持向量机)模型应用到振动机械故障诊断实例中,其结果表明相较于传统神经网络,PSO-SVM具有更高的准确性。
随机森林是通过集成学习的思想将多棵树(决策树)集成的一种算法,有着较高的准确率、可解释性及能够评估各个特征重要性等优势。Wang[9]等人通过提取振动信号的无量纲指数做为特征参数,利用随机森林训练,预测精度高达100%。马富齐[10]利用随机森林的特性通过剔除掉冗余的特征向量,进行了对机组的故障诊断。单增海[11]等人将得到的多传感器信息融合后,进行特征筛选,利用多粒度级联森林模型完成了对液压泵健康状态评估。段智勇[12]等人利用随机森林算法对屏蔽泵进行故障诊断,并取得了满意的效果。徐书凡[13]将潜油螺杆泵井的参数数据输入随机森林模型,完成了对潜油螺杆泵采油系统故障诊断。
当前在针对离心泵转子故障能够评估其故障特征重要性特征的研究较少,并且非重要特征之间的相关性会进一步削弱故障识别的效果,从而影响故障诊断效率及准确率。本文旨在通过随机森林对提取出的故障特征重要性进行分析、筛选,结合PSO-SVM 对离心泵转子常见故障状态进行识别。通过在离心泵上放置振动加速度传感器进行原始信号采集,利用时域、频域处理方法,提取原始信号的时、频域特征参数矩阵,通过随机森林得到重要性较高的特征,并将之与随机森林分类得到的分类结果进行组合,得到新的故障特征参数矩阵,进入PSOSVM 中进行训练、验证。这样既能降低非重要故障特征对离心泵转子故障识别效果的影响,也能减少故障特征参数矩阵的维度,从而减少冗余的故障信息,降低计算的复杂程度。
1 随机森林计算特征重要度原理
随机森林(Random Forest,简称RF)是Bagging 的一个扩展变体[14]。它首先基于bagging 思想,无放回的可重复的对初始数据集进行采样,再利用这些采样集训练决策树,同传统决策树选择特征(信息增益)不同的是RF 选择特征时随机从特征集中抽取一部分特征子集,并从这些子集中选择一个最优属性用于构建决策树的节点,进行下一步的分裂。由于构建每一颗决策树时是从数据集中进行随机可重复进行采样,因此还有部分数据集是没有被采样到的,这部分数据称为袋外数据(oob),将这部分数据代入已建立的决策树中,可以用于计算决策树的预测错误率(袋外数据误差,oobErr)。
由于原始信号具有信息量大、特征隐蔽和包含较多的噪声等特点,单纯直观分析无法获得被监测对象的具体健康状态信息,因此需要通过不同的信号处理方法对原始信号进行转换和处理,从而提取出能够反映运行设备的状态特征信息[15]。均方根值、峰值、峰值因子、峭度、脉冲因子、裕度因子和波形因子是振动信号进行时域统计分析最常用的参数指标[16]。为了更多反应原始信号携带的特征信息。另外选取了较为常用的4个时域特征和3个频域统计指标,时域特征为方差、均值、峭度因子、偏度;频域为重心频率、均方根频率、标准差频率。本文统计共14个时、频域指标作为故障特征的统计指标,计算公式如表1。
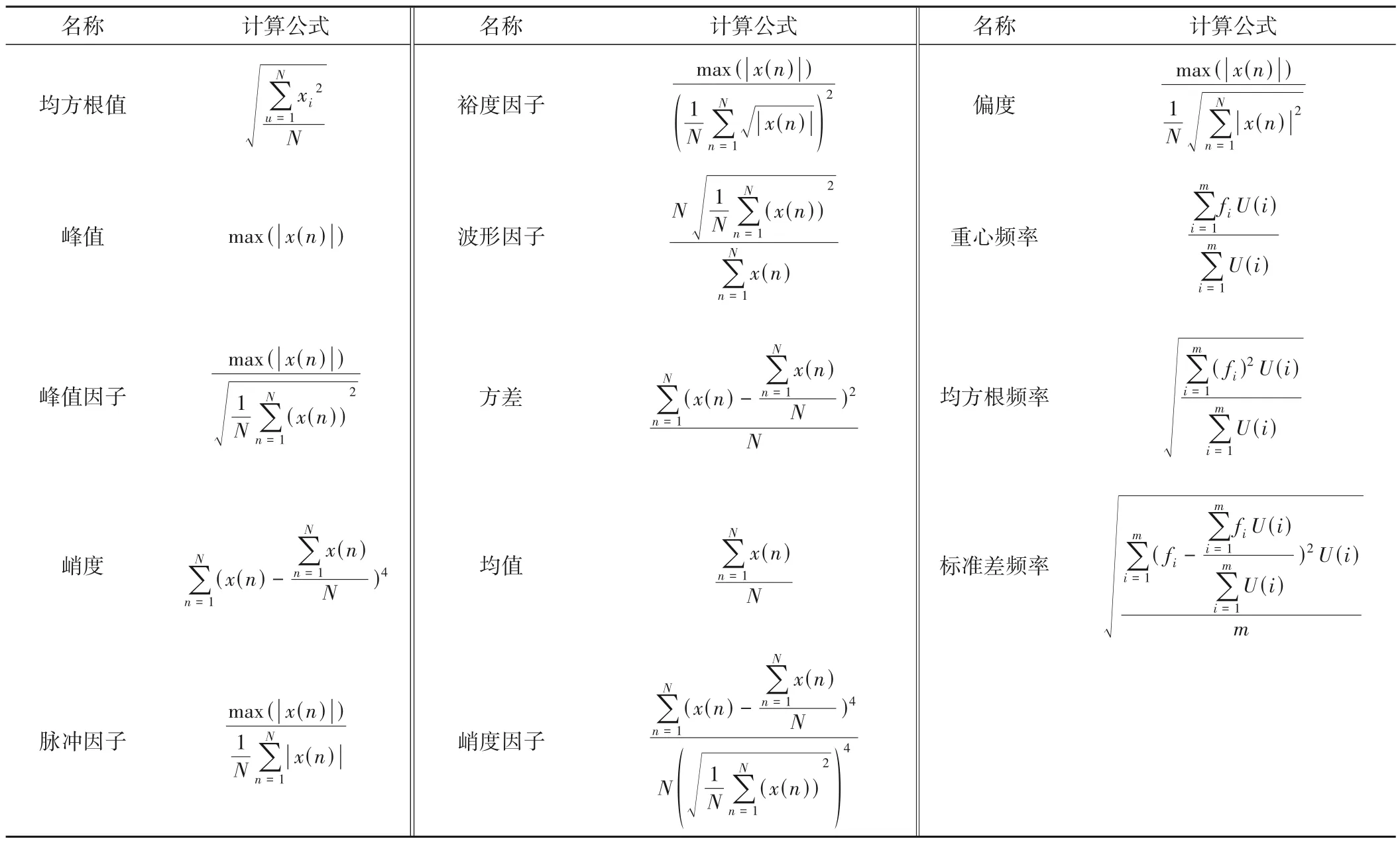
表1 特征计算方法Tab.1 Calculation method of characteristics
表中的x(n)为信号的时域序列,n=1,2,3,…,N,N为样本点数;U(i)表示的是信号x(n)的频谱,其中i=1,2,3,…,m,m为谱线的个数;fi表示的是第i根谱线的频率值。
对于随机森林中某个特征重要性a的计算步骤如下:
(1)假设随机森林中共有n颗决策树,对于一棵树Ti,其中i=1,2,3,…,n,用袋外数据oob(i)代入已建立的决策树Ti中,计算该树的袋外数据误差,记作oobErr01(i)。
(2)然后随机置换oob(i)中第j列的特征参数,置换的方法是通过permutation 方式将oob(i)中所有样本的第j个特征参数重新打乱分布,保持其他特征参数不变,重新计算该树的袋外数据误差,记作oobErr02(i)。
(3)则该特征重要性a的计算公式如下:
若加入噪声后袋外数据准确率下降,即oobErr02(i)上升,特征重要性a增大,则该特征重要程度比较高。
本文利用随机森林算法和PSO-SVM 进行离心泵转子不平衡、不对中故障诊断的流程图见图1。

图1 诊断流程图Fig.1 Diagnostic flow chart
2 离心泵转子不平衡、平行不对中故障实验
以一台离心泵作为实验对象,离心泵的主要参数为:额定流量10.6 m³∕h;额定转速2 900 r∕min;额定扬程26 m;比转速49.88。信号采集选用的振动加速度传感器精度为±1%。
振动加速度传感器布置在离心泵进口法兰水平径向。实验过程中先调节变频电机的转速使其达到设定转速,然后调节泵的出口阀门,使其达到设定的流量位置,待运行稳定时采集数据。
转子不平衡故障复现时分别用2.6、6.3、9 g 的配重块安装在联轴器的螺栓上,使其产生质量偏心。不同重量的配重实验时,配重块安装在同一位置。为了提高该诊断模型在不同工况下的诊断率,根据泵的相似定律,每个配重实验分别在0.7n、0.85n、1.0n转速工况,0.7Qn、0.85Qn、1.0Qn流量工况下进行,共27组实验。

图2 实验现场测点布置图Fig.2 Layout of experimental points
转子平行不对中故障复现时,通过移动电机的位置,使转子产生不对中现象。不同平行不对中故障(30 丝、40 丝、50 丝)实验时,分别在0.7n、0.85n、1.0n转速工况,0.7Qn、0.85Qn、1.0Qn流量工况下进行,共27组实验。
3 实验数据分析与处理
实验所用传感器采集设定采集频率为25 600 Hz,采样时间1 s。其中正常、不平衡、不对中在1.0n、1.0Qn工况下进口法兰水平径向的振动加速度信号时域图形如图3所示。

图3 不同设备状态下时域图Fig.3 Time domain diagram under different device states
由于不平衡、不对中的特征频率主要出现在低频段,本文分析频谱图时只截取0~500 Hz作为分析频段。
图4为正常工况下、不平衡程度为6.3 g、不对中程度为30丝时额定转速、流量的轴承座测点的频域图。不平衡工况下对比正常工况下的频域图,可以看到图中一倍频(48.33 Hz)的幅值有所增大,这符合不平衡故障发生时的特征表现,频谱图中出现6倍频是由于实验泵所用叶轮为6叶片叶轮,出现的6倍频为叶频。不对中工况下对比相较于正常工况下的频域图,可以看到频谱图中二倍频的幅值有所增大,同时一倍频幅值有所降低,这符合转子平行不对中故障发生时的特征表现。

图4 频域图Fig.4 Frequency domain diagram
4 模型训练与分析
将实验采集获得的数据进行处理,按照上节特征提取方法提取故障特征参数,得到一个315×14的故障特征矩阵并进行标签标记,采用模型训练方法主要分为以下几个步骤进行。
(1)故障特征集再构建,将故障特征集作为随机森林的输入,利用随机森林每次会有约1∕3 的样本没有参与决策树的建立,得到每个特征的重要性测度指标,将重要性前6个的故障特征及随机森林分类器得到的分类结果作为新特征集的组成,得到新故障特征集。
(2)SVM 算法属于有监督学习算法,是最优秀的分类算法之一,广泛的应用于科学技术领域,因此本文选择SVM 为故障识别的学习算法。由于支持向量机(SVM)中核函数半径(g)、惩罚因子(c)难以选择最优的[17],本文选择RBF 作为SVM 的核函数,利用粒子群优化支持向量机(PSO-SVM),寻找最优的粒子点为SVM 的最优核函数半径和惩罚因子。将得到的新故障特征集等比例分组,50%作为SVM 的训练集,用于训练模型;50%作为SVM的测试集,用于验证模型。
本文中,随机森林决策树数量设为400,最小叶节点设置为5,将原始特征矩阵输入得到每个特征的重要性评估由大到小排序如图5所示。

图5 特征重要性评估Fig.5 Characteristics importance evaluation
取重要性排序前6 的特征分别为峭度、方差、均方根、重心频率、均方根频率、标准差频率。同时将随机森林分类器得到的不同故障的分类概率结果作为新的故障特征,同重要性较高的6个特征最终得到一个新的315×9特征集。
4.1 支持向量机诊断的结果对比
故障特征矩阵进行分组,分组情况如表2所示。

表2 故障特征分组情况Tab.2 Grouping of fault features
将分组后的原始故障特征矩阵与新故障特征矩阵的训练集分别输入PSO-SVM 中进行分类训练,PSO-SVM 适应度曲线如图6所示,从图6中可以看出重构后的原始特征在通过PSO算法计算最佳的适应度在经过第4 次迭代后达到最优,此时的最优核函数半径g等于0.01,惩罚因子c等于12.395 9,SVM 训练精度100%,相较于原始特征矩阵输入SVM 中通过PSO 算法计算最佳的适应度在经过第33次迭代后达到最优,训练精度为85.6%,无论是迭代次数还是训练精度都有大幅度改善。

图6 PSO-SVM 适应度曲线Fig.6 PSO-SVM fitness curve
利用测试数据进行故障诊断,得到的结果如图7。从图7中可以看出利用原始故障特征集进行验证时有大部分正常状态下的数据被识别成了不对中或不平衡,模型对正常状态下的故障特征数据识别表现不好,不能很好的区分正常与不对中故障。数据显示重构特征矩阵训练的SVM 故障诊断模型对测试集的分类精度达到99.36%,相较于原始故障训练的SVM 故障诊断模型的识别精确度86.7%,对故障的识别精度有明显的提升,其部分诊断概率详情见表3。

表3 进口法兰水平径向测点部分概率详情Tab.4 Partial probability details of inlet flange horizontal and radial measurement points

图7 进口法兰水平径向测点PSO-SVM 诊断结果Fig.7 PSO-SVM diagnosis results of horizontal and radial measurement points of inlet flange
5 结 论
利用随机森林筛选出的重要特征,并将其与随机森林的分类结果重新组合形成新的故障特征矩阵,通过将原始特征矩阵与重构后的特征矩阵分别输入进PSO-SVM,得到每组特征向量对应不同标签的预测结果,主要的结论如下。
(1)重构后的故障特征矩阵在进入PSO-SVM 中进行训练时,表现出更好的适应度,在寻优过程中仅迭代4 次,便达到最佳训练精度,且训练精度明显高于原始故障矩阵的训练精度,达到100%;
(2)进行模型精度测试时,重构后的故障特征矩阵表现明显好于原始故障特征矩阵,其测试精度达到99.36%,能够明显区分出正常、不对中、不平衡下的数据。

