并联水库群共同供水任务分配规则研究
万 芳,靳 玮,柴启辉,张 飞
(1.华北水利水电大学,河南 郑州 450045;2.开封市柳园口灌区管理所,河南 开封 475000)
水库群共同供水任务如何在水库间进行合理分配是影响供水调度效果的重要环节,水库群供水调度分配规则研究较多[1-4],但目前关于共同供水任务分配规则的研究较少,旨在确定水库群对各用户的供水水平和每个成员水库分别承担的供水任务,其作用是回答“对用户供多少水”和“由谁供水”的问题,对于供水水库群,由于共同用户的存在,使得水库群联合供水需要解决共同供水任务分配问题。对于并联供水水库群,通过共同用户相互联系,不仅要参照每个成员水库的状态特征确定供水决策,还要根据每个成员水库的状态特征合理分配共同供水任务。李昱等[5]通过构建两个虚拟聚合水库和相应联合调度图,分别应用分水比例法和补偿调节法对并联水库群和梯级水库群共同供水任务进行分配;Chang 等[6]利用补偿调节的方式对翡翠水库、玉石水库群进行供水调度;以发电为主的梯级水库群分配中,一般通过利用供需水判别式法[7,8]以蓄、供水期增发电量尽可能大、损失电能尽可能小为基本原则,确定水库蓄水供水顺序,达到优化目的,通常系统中判别式值大的水库在蓄水期优先蓄水,判别式小的水库在供水期优先放水,但蓄供水判别式存在增大系统弃水、缺乏对水量分配的考虑[9];Wu等[10]将水库群等效为一个聚合水库,引入动态供水因子作为成员水库间供水分配原则,其中供水分配因子根据水库当前的可供水量确定,且认为与当前时段的可供水量成正比,但没有考虑成员水库的供水顺序;Wang 等[11]引入目标蓄水量的概念,根据供水量与目标供水量、联合供水任务以及供水分配系数之间的相关关系,实现水库间联合供水的分配,并采用库容系数法对共同用户进行供水,但该方法在分配供水量的过程中没有考虑供水顺序。
对于并联水库,Chang 等[12]通过在某一成员水库单库调度图上添加联合供水调度线,根据成员水库蓄水量与联合供水调度线之间的位置关系决定哪个水库对共同供水用户进行供水;Guo 等[13]将库群系统聚合成等效水库,根据系统整体蓄水量与聚合水库调度图供水控制线的位置关系,制定水库群对共同用户的供水决策;参数式规则[14]是确定水库蓄放水次序与蓄水量空间的主要方法,但不能表达出水库蓄水空间与水库调节性能之间的关系;New York City Rule 和Space Rule 是在蓄水期调度中尽量减少系统中当有些水库弃水时而其他水库尚未蓄满的情况[15],在大多数情况下可得到最优或近似最优解,但目前尚没有较明确的蓄、供水期的划分标准,且难以指导调度操作;胡铁松等[16]基于并联供水水库两阶段调度问题的最优性条件,设计了并联水库调度问题的优化求解方法。平衡曲线法[17,18]用分段性关系描述并联水库系统总蓄水量与各库蓄水量之间的关系,此方法简单明了,但与独立用户的复杂系统难以结合,没有考虑并联水库分别独立承担的供水量,且认为并联水库余留期来水量具有相同的概率分布,只有距离较近的水库群才能满足这些条件,不具有普遍性,故论文应用平衡曲线进一步研究并联水库群空间蓄水量的合理分配规则。
复杂水库群联合供水调度种类繁多,关系复杂,既相互影响又相互制约,由于其在时空上水量分配的复杂性、动态性[19,20],制定科学、合理有效的共同供水任务的水库间分配规则,从而减少弃水量,提高供水保证率,是论文解决的重点内容。首先建立平衡曲线对并联水库群共同供水任务分配进行研究,揭示并联供水水库群间水量分配规则,进一步完善复杂水库群供水调度理论体系。
1 研究区概况
滦河是北方地区较丰沛的河流之一,多年平均径流量为46.94 亿m3,年际水量分配不均,具有连丰连枯的水文特性。而随着下游天津、唐山水资源供需矛盾日益突出。联合调度水库群包括潘家口、大黑汀、于桥、邱庄和陡河水库,其中潘家口水库年均径流量为24.50 亿m3,为多年调节水库;大黑汀水库位于潘家口水库下游,属于潘家口水库的反调节水库,为年调节水库;桃林口水库位于秦皇岛市滦河支流的青龙河上,是一座综合性的大型水库;于桥水库属于天津市一座最大的大型水库;邱庄水库是引滦入唐沿线上的中间调节水库;陡河水库位于唐山市以北15 km的陡河上游。水库间地理位置见图1。
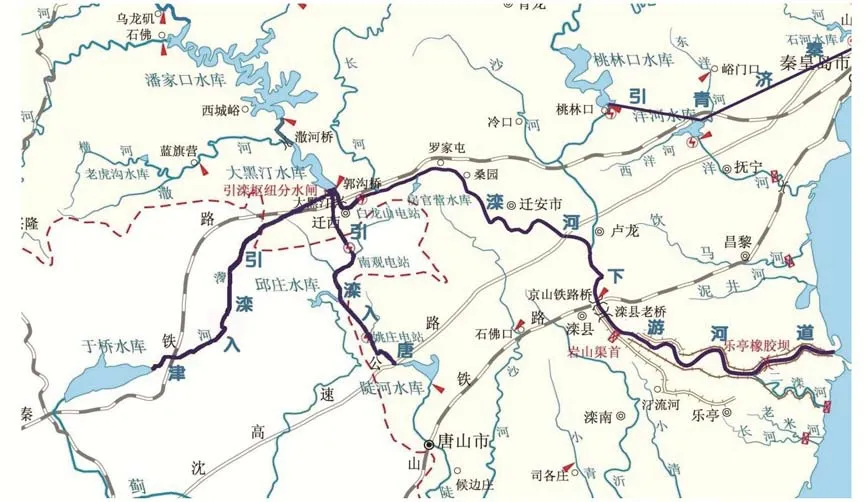
图1 水库间地理位置Fig.1 Geographical position among reservoirs
滦河下游水库群供水系统主要包括潘家口、大黑汀、于桥、邱庄、陡河和桃林口水库,主要供应天津、唐山、秦皇岛三市的城市生活用水、工业用水并向滦河下游农业灌溉。潘家口水库为多年调节水库,故由潘家口、大黑汀水库向于桥、邱庄、陡河水库补充供水;且潘家口、大黑汀和桃林口水库共同给滦河下游农业供水。其水库间的水力联系见图2所示。水库的特征参数如表1所示。
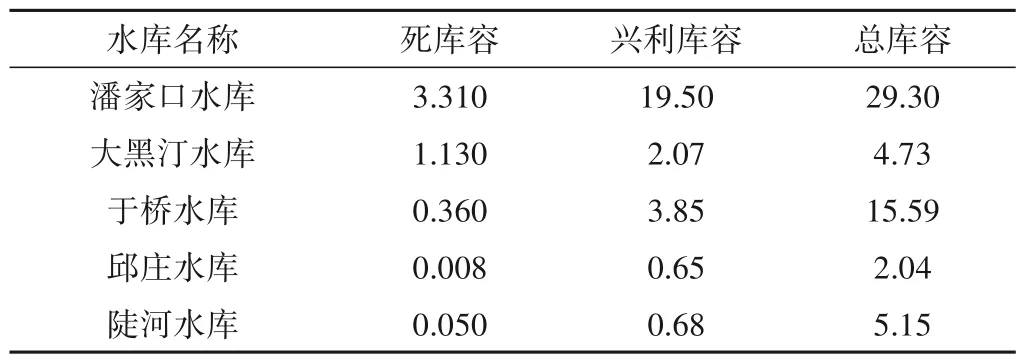
表1 各水库主要工程特性指标亿m3Tab.1 Main project characteristic indexes of each water supply reservoir
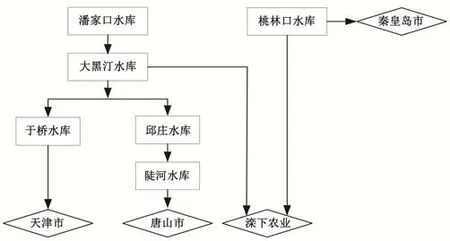
图2 水库间水力联系网络图Fig.2 The diagram of hydraulic connection network among reservoir group
邱庄、陡河水库为串联水库群共同向唐山市进行供水。对于研究的多水源、多用户的水库群对象,系统规模庞大、结构复杂,故首先将水库群供水系统进行聚合。其系统聚合见图3。
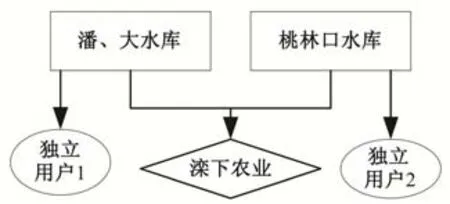
图3 水库群系统聚合图Fig.3 Aggregation diagram of reservoir group system
潘、大水库与桃林口水库为并联供水群共同向滦河下游农业供水,其中将潘家口、大黑汀水库聚合为“潘、大水库”;“独立用户1”为于桥水库、邱庄和陡河水库分别给天津市、唐山市供水,将水库和用户进行聚合,供水分解图见图4;“独立用户2”为秦皇岛市供水。
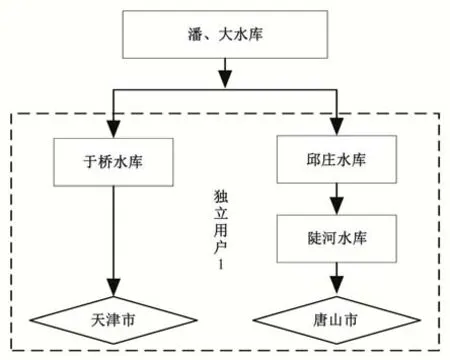
图4 潘、大水库给独立用户1供水分解图Fig.4 Water supply decomposition diagram for independent users1 of Pan and Da reservoir group
2 水库群供水调度模型
以供水区缺水率f1最小,弃水量f2最小为目标函数,建立水库群供水调度模型。
目标函数:
约束条件:
其中:
其中:ρL≤5%;ρI≤10%;ρA≤30%。
式中:i和N分别为水库序号和系统水库总数;t和T分别为调度时段和时段总数;Rit、Git、Qit分别为i水库t时段需水量、供水量、弃水量;R(1)it、R(2)it分别为i水库t时段独立需水量和共同用户需水量;G(1)it、G(2)it分别为i水库t时段独立供水量和对共同用户供水量;Vit、Vit+1分别为i水库时段初和时段末的蓄水量;Iit、Sit分别为i水库t时段入库流量和蒸发渗漏等损失水量;Vit,min一般为死库容,Vit,max为允许的最大库容,非汛期一般为正常蓄水位下的库容,汛期为防洪限制水位下的库容;水量及库容的单位为m3;ρ为用水户允许的破坏深度;ρL、ρI、ρA分别为供水区生活、工业、农业的最大破坏深度;且所有变量为非负约束。
将混联水库群分别划分为串联水库群系统和并联水库群系统,根据水库间不同的水利关系分别进行共同供水任务的分配研究。共同供水任务在水库间分配规则主要包括两个方面:①根据各水库当前蓄水状态,确定水库群对各用户是限制供水还是按需供水,即确定系统总的供水量;②按照一定的分配规则将共同供水任务分配到串联或并联的各成员水库,制定合理的蓄水量分配规则,即确定由某个水库供水。
以图5、6所示的串联、并联水库为例,各水库除了承担各自独立用户供水任务外,还有共同供水任务,其中独立用户供水量确定与单库供水规则相近。但在进行共同供水任务水量分配时,不仅要确定串联系统或并联系统总的共同供水量,还要考虑各水库的蓄水状态,根据每个任务水库的状态特征合理分配共同供水任务。其中串联水库间共同供水任务的关键是合理确定上游水库对下游水库的下泄量;并联水库是通过共同供水用户联系起来的。

图5 串联水库共同供水示意图Fig.5 Schematic of common tasks allocation in series
图5中,m、n分别为串联成员水库和并联成员水库的个数;且m+n≤N。
对于串联两库i- 1,i在某调度时段t供水调度的情况,采用作者提出的优先度原理[21]对串联水库群共同供水任务进行分配,既减少水量损失,又缩短供水流达时间。
3 并联水库群共同供水任务分配规则
3.1 基于平衡曲线的分配规则

图6 并联水库共同供水示意图Fig.6 Schematic of common tasks allocation in parallel
由于并联水库群是通过共同供水任务产生的水利关系,因此其蓄水空间分配问题更加复杂。如图2所示,每个水库都有独立供水要求,故先按单库调度规则,满足独立用户用水要求,重点求解G(2)it,即i水库t时段给共同用户的供水量。通过拟定合理的平衡曲线,描述调度时段末系统总蓄水量U与成员各库理想蓄水量V*it之间的关系,指示系统蓄水量在各成员水库中的最佳分布。
约束条件:
(1)水量平衡约束:
(2)系统对共同供水用户总供水量约束:
(3)平衡曲线约束:各库目标蓄水状态或实际蓄水状态之和等于系统总蓄水量。
(4)平衡曲线突变点约束(如图7所示)。
(5)变量非负约束。
式中:V*it、Vit为各成员水库t时段目标蓄水量和实际蓄水量、Ut为t时段并联水库系统总蓄水量,它们之间的关系是合理确定平衡曲线的关键问题;Gt为t时段并联水库系统为满足调度目标的供水总量,其定义为各成员水库t时段对共同用户供水量之和,且要求不小于t时段共同用户的最小供水量Rmint,不大于t时段共同用户的需水量Rt。
由于在水库群供水调度中,汛期及非汛期的来水、供水的不同,导致各库蓄水量的变化,因此,平衡曲线具有不同调度时期的分段性。即每段具有不同的斜率,假设并联水库由2 个成员水库组成,无论供水期还是蓄水期,平衡曲线统一采用3 段4节点进行表述,则平衡曲线示意图如图7所示。

图7 平衡曲线示意图Fig.7 Schematic diagram of the balancing curves
当水库入流大于需水时,库群系统需要存储多余的水量,因此通过对比不同分段内各成员水库平衡曲线的斜率,表明水库系统对共同供水任务在各成员水库中的分配情况。平衡曲线具有如下特征:
(1)由于各水库的蓄水量不大于并联水库群总蓄水量,斜率为0、1 或来水比例,故各成员水库在每段的斜率均在[0,1]之间;
(2)各库蓄水量之和等于系统总蓄水量,故在任意两个拐点之间成员水库的斜率之和等于1。如图7所示,mu3拐点之后水库2 的斜率为0,则水库1 的斜率必为1,物理意义表示:系统蓄水量的变化不改变水库2 的蓄水状态,多余水量不存放在此库中,而是全部存于水库1中;
(3)由于平衡曲线的横坐标为系统总蓄水量,因此横坐标中不包含成员水库的编号,且每个成员水库具有相同的拐点个数,且拐点横坐标都是一样的,因此平衡曲线拐点的坐标为(urt,vrit),其中r=(mu1,mu2,…,Mu),mu、Mu分别为拐点的序号和总数。图8中第一个和第四个拐点坐标已知,分别为:(Umin,Vimin)、(Umax,Vimax)。假设第二个、第三个拐点坐标分别为:(umu2t,)、(umu3t,),可由调度期末系统蓄水量插值得到两个拐点间坐标(Ut,V*it),则V*it即为i水库t时段末的目标蓄水量,从而在任何时段可对共同供水进行水量分配。

图8 以V*i,t+1为例的示意图Fig.8 An example of solution of the V*i,t+1
则:
3.2 平衡曲线关键点的优化
平衡曲线的确定重点是确定各成员水库拐点坐标及各分段的斜率,以便更好地对各成员水库蓄水进行分配,为制定合理的供水任务分配规则提供依据。在并联水库系统中,优秀的供水规则应使成员水库有较大的供水能力和较高的成员水库蓄水率同步性(即:成员水库力求同时达到蓄满或放空状态)。依据以上性质及各种约束,首先分析各拐点变化情况,如图9所示。

图9 平衡曲线拐点变化分析示意图Fig.9 Diagram of the analysis on the change of the inflection point of the balancing curve
由于系统来水、用水的随机性和不确定性,导致平衡曲线拐点的变化具有随机性,如图9中,以一个水库i为例,拐点由mu2 点变到mu2′点,则:拐点的纵横坐标产生变化,水库i拐点间的平衡曲线斜率也随之改变;成员水库中其他水库的拐点及相应的斜率也将产生变化。假设拐点的横纵坐标位移分别为Sdxt、Sdyt。
式中:xp、yp为(0,1)之间的随机数。
基于以上平衡曲线分配规则理论分析,以聚合水库调度图确定系统各时段的总供水量,以分段拐点和直线斜率为决策变量,采用3 段4 节点的平衡曲线分段形式进行表述,各成员水库拐点坐标确定以后,分段直线的斜率即可相应得到。基于以下原理及假定,确定拐点参数的个数:
假设有N个成员水库,由约束条件(13),各库蓄水状态之和等于系统总蓄水量,且在任意两个拐点之间成员水库的斜率之和等于1,故在每个t时段,只有N- 1个水库的平衡曲线需要估计;无论是供水期还是蓄水期,并联水库系统平衡曲线都具有分段性,其中分段数随着并联水库数量的增加而增加,且水库平衡曲线的拐点坐标和斜率的变化都是随着水库的蓄水、来水、供水的变化而变化;假设有MU个拐点,则有MU- 1段连接直线,如图9所示,第一个和最后一个拐点坐标已知,分别为:(Umin,Vimin)、(Umax,Vimax),故只有MU- 2 个拐点需要估计;每个成员水库具有相同的拐点个数,且拐点横坐标都是一样的。因此,由有N个成员水库组成的并联水库、每个水库的平衡曲线有MU个拐点,则有NDE个参数需要确定:
如:MU=5,N=2(图10所示)。
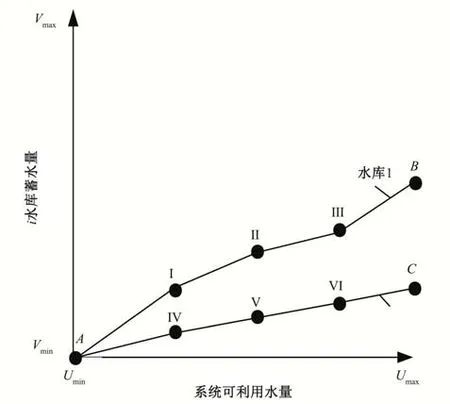
图10 平衡曲线拐点参数确定示意图Fig.10 Diagram of the parameter determination on the inflection point of the balancing curve
其中A、B、C三点坐标已知,假设水库1 中Ⅰ、Ⅱ、Ⅲ三个拐点的坐标分别为(a,y1)、(b,y2)、(c,y3),则水库2中Ⅳ、Ⅴ、Ⅵ三个拐点的坐标分别为(a,y4)、(b,y5)、(c,y6),需要确定的参数有9个,分别为:a,b,c,y1,y2,y3,y4,y5,y6。验证公式(21)的合理性。
采用作者提出的基于免疫进化的粒子群算法(IEAPSO)[22]对关键点进行优化,粒子群算法(Particle Swarm Optimization,PSO)作为一种高效并行优化方法,能够实现复杂空间中最优解的搜索分析,适用于求解一些非线性、不可微、多目标的复杂优化问题,但优化程度得不到保证,易陷入局部最优,且对初始种群有较大依赖性。免疫进化算法(Immune Evolutionary Algorithm,IEA)具有高度的全局性,但其局部搜索效果较差,且常出现进化缓慢的现象。因此,此论文提出基于免疫进化算法的粒子群优化算法(IEA-PSO),利用免疫进化算法的全局搜索特点,弥补粒子群算法的不足。在算法初期采用免疫进化算法进行全局搜索,根据粒子群中设置的群体规模M来确定免疫进化算法的进化代数K,即:使得K=M,将免疫进化算法中每次迭代生成的最优M个个体作为粒子群算法的初始粒子。同时取免疫进化算法中最优的个体作为粒子群群体中的邻域极值,并根据粒子群中各个粒子与邻域极值的差异来确定各个粒子的初始速度,其确定原则是:距离邻域极值越近的粒子初始速度越小,越远的粒子初始速度越大。然后再利用粒子群算法进行局部搜索,以加快算法后期的收敛速度。求解并更新平衡曲线的拐点,并基于平衡曲线对并联水库共同供水任务进行分配。其中算法流程图见图11所示。

图11 基于平衡曲线并联水库共同供水任务优化流程图Fig.11 The algorithm flowchart of allocation common water supply task of parallel reservoirs based on the balancing curves
4 实例分析
4.1 计算结果
(1)以水库群57年(1962-2018年)长系列天然入库径流、天津、唐山、秦皇岛、滦河下游农业需水量为输入资料,将水利年度划分为汛前(4-6月份)、汛期(7-9月份)、汛后(10-12月份)、干旱期(1-3月份)4个调度时段,首先应用优先度原理对串联水库群(邱庄水库、陡河水库)共同供水任务进行分配,调度结果见表1所示。
(2)根据水利年度的划分,设置并联水库群共同供水任务的平衡曲线的分段,并以关键点为决策变量通过模拟长时序调度,经优化模型进行修正,在IPSO算法中,免疫进化的群体规模设置为P=80,其中进化代数K=M=60,并经过多次计算证明,其参数取值分别为A=4、σε=0、α=1.8、β=3.5;粒子群优化算法中,设置惯性权重w=0.5、加速常数c1=1.5,c2=2.0、迭代代数Ks=100。为了检验所提出的调度规则与优化模型的有效性,在表3计算结果中同时给出动态规划和补偿调节的结果。

表3 潘大、桃林口水库并联水库群联合调度结果Tab.3 The regulation results of Pan-Da and Taolinkou reservoirs with different scheduling scheme
由表3可知,平衡曲线得到的库群系统供水量较补偿调节增加约5%,弃水量减少10%左右,与动态规划得到的年均供水量、年均弃水量及保证率接近,在一定程度上反映平衡曲线的合理性;由于在并联水库群供水系统中,优秀的供水调度规则使成员水库在枯水期同时达到空库的概率相同或蓄水率(各库蓄水量占兴利库容的比例)成正相关性,在蓄水期发生弃水的概率相同。
4.2 计算结果分析
(1)对于串联水库群的共同供水任务分配,水库群供水调度的复杂性不仅是由于变量维数的增加,主要是由于水库群之间的水力补偿关系,水库群的供水次序为自下而上原则,下游各水库(陡河水库)将本库的天然入流和有效蓄水利用智能优化算法配给供水区,当水量不足时要求上一级水库(邱庄水库)放水补给。水库间供水应遵循“有弃水无缺水,有缺水无弃水”的原则,即:当第一个水库(邱庄水库)产生弃水时,使弃水进入下一个水库(陡河水库)中进行调节,以此类推一直到末水库,如果依然产生弃水,将其视为弃水量。因此,这种情况,在水库群供水过程中应该考虑,将多余的水量储存在某个水库中,从而使得水库供水的水量损失最小;同时,在供水区缺水的情况下,如何以最快的速度供给供水区,缩小供水流达时间;当末水库库容达到库容下线(通常为死水位)时,供水区仍产生缺水时,不能作为供水区的最终缺水状态,因为它上一水库可以对其进行补偿调度,以此类推一直到第一个水库(邱庄水库),如果依然产生缺水,则将视为供水区的最终缺水状态,在这种情况下应从水库群的末水库(陡河水库)算起直到第一个水库(邱庄水库)。由表2可知,邱庄水库年均弃水量为256 万m3,占兴利库容(6 500 万m3)的3.9%;陡河水库年均弃水量为487 万m3,占兴利库容(6 840 万m3)的7.1%。
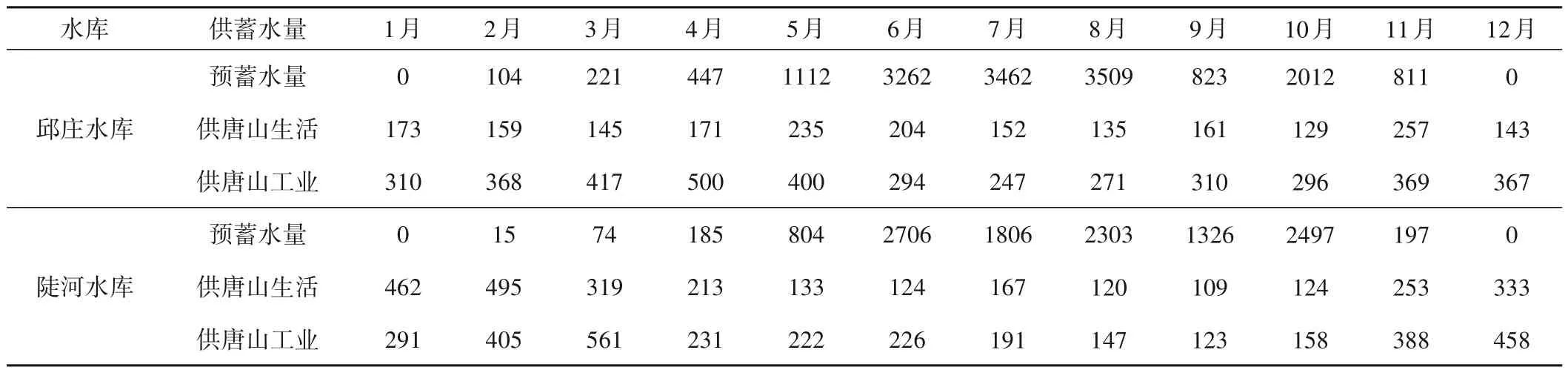
表2 水库群多年平均供水调度结果万m3Tab.2 The results of reservoir group for annual average water supply dispatching
(2)对于并联水库,图12分别为平衡曲线和补偿调节方案下潘大、桃林口水库的蓄水率(αP,αT)散点图,分析并联水库蓄水率的相关性。
图12结果表明,平衡曲线调度方案下,潘大水库与桃林口水库的蓄水率分别为0.70、0.59,潘大水库蓄水率较高主要由于独立用户1 的供水需求量比较大,除了在并联水库系统中满足共同供水任务外,还要兼顾独立用户;补偿调节调度方案下,潘大水库与桃林口水库的蓄水率分别为0.85、0.32,差别比较大,主要由于补偿调节中划定了水库群的蓄放水顺序,但未考虑径流间的补偿作用。平衡曲线和补偿调节得到的相关系数分别为0.88、0.35,显然,平衡曲线得到的并联水库群的同时蓄满和放空更具有同步性。
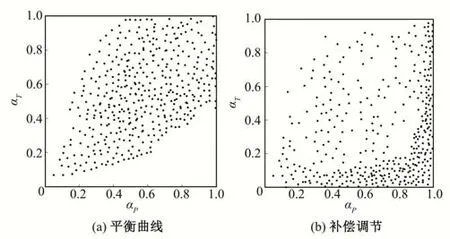
图12 不同调度方案的蓄水率分布Fig.12 Distribution of water storage rate with different scheduling schemes
图13、14分别给出汛期和非汛期并联水库的平衡曲线图,其中Z1、Z2分别为潘大水库、桃林口水库在当前调度时段的蓄水上限(汛期:Z1=21.57 亿m³,Z2=7.09 亿m³;非汛期:Z1=18.26 亿m³,Z2=7.09 亿m³),其中潘大水库的蓄水量为相应时段潘家口水库与大黑汀水库蓄水量之和。
由图13、14可以看出,两库曲线的斜率无论在汛期还是非汛期均从蓄水下限开始以低于1 的斜率延伸到蓄水上限。图13中在汛期潘大水库先蓄水,然后两库同时蓄水,为了减少桃林口水库的弃水量使两库发生弃水时处于同步蓄满状态;图14中非汛期时,两库同时放水,但由于潘大水库库容较大,故下泄水量较大(斜率较桃林口水库大)。

图13 汛期平衡曲线图Fig.13 Balancing curve of flood season
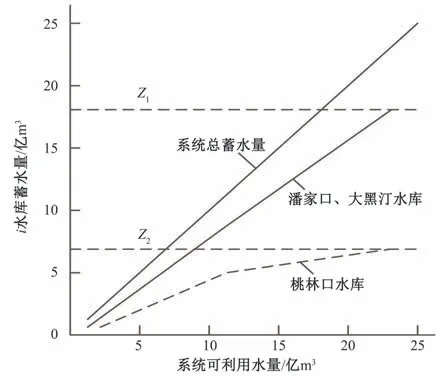
图14 非汛期平衡曲线图Fig.14 Balancing curve of non-flood season
5 结 论
通过拟定合理的平衡曲线,制定含有供水约束与独立用户的并联水库系统共同供水任务的分配机制,确定并联水库群共同供水任务的分配比例,以不同拐点和斜率描述平衡曲线的分段性,表征汛期、非汛期各水库蓄水量及供水量的变化,以缺水率最小和弃水量最小为目标函数建立优化模型对分配规则进行修正,并采用基于免疫进化的粒子群算法率定平衡曲线的决策变量突变点及斜率,最终得到相对优秀的供水规则。以滦河流域下游水库群为研究对象,计算结果表明:①拟定合理平衡曲线对并联水库群共同供水任务进行分配,其库群系统供水量较补偿调节增加约5%,弃水量减少10%左右,与动态规划得到的最大供水量、年均弃水量及保证率接近,在一定程度上反应平衡曲线的合理性;②平衡曲线能够得到相对优秀的供水规则——成员水库有较大的供水能力和较高的成员水库蓄水率同步性,潘大水库与桃林口水库的蓄水率分别为0.70、0.59;③水库间供水任务分配比例与其兴利库容的比值接近,也进一步说明了平衡曲线在分配共同供水任务中的合理性。

