基于索引调制OTFS 系统的应用

丁鹏鹏，和青山

（福州大学 先进制造学院，福建 泉州 362200）

0 引言

为了应对高移动性场景的挑战，HADANI R 提出了正交时频空（Orthogonal Time Frequency Space，OTFS）新型调制方案[1]。与传统的正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）调制相比[2]，OTFS 展现出更为卓越的性能。在OTFS 中，所有的传输符号都可以在延迟多普勒（Delay Doppler，DD）域复用，并在时频域扩展，充分利用了快时变信道的特性。同时，OTFS 利用了快时变信道中的延迟和多普勒维度上的分集增益能够将快时变信道转化为DD 域中的二维准时不变信道，极大地降低了接收端信道估计和符号检测的复杂度[3]。

索引调制（Index Modulation，IM）是无线通信中一种非常有前景的调制技术，具有高频谱效率和高能量效率。IM 方案中，除了通过星座符号载波传输信息比特外，还可以通过子块的索引传输[4]。在该方案中，多种类型的传输实体（如天线[5]、频率时隙[6]等）均可用于承载索引比特而不需要额外的能量消耗。考虑到IM 的显著优越性，文献[7]提出了新型结合索引调制的正交时频空（Orthogonal Time Frequency Space with Index Modulation，OTFS-IM）系统。OTFS-IM 不仅继承了OTFS 对多普勒频移不敏感的优点，而且在高移动场景下展现出比OTFS技术更为卓越的误码率（Bit Error Rate，BER）性能。最小均方误差结合最大似然方案（Minimum Mean Squared Error with Maximum Likelihood，MMSE-ML）在文献[7]中被提出，但该算法的复杂度极高，不利于在图像传输场景中的实现。

OFDM技术在图像传输方面的应用已经成熟[8]，但是OFDM 技术本身难以对抗较大的多普勒频偏。考虑到OTFS 和IM 的优势，本文拟将OTFS-IM 应用到图像传输中。广义近似消息传递（Generalized Approximate Message Passing，GAMP）算法[9]已被证明能够在OTFS 系统中在BER 性能和计算复杂度之间进行灵活的权衡，故本文提出的算法是在GAMP 算法上进行改进。

1 OTFS-IM 系统

1.1 IM 调制

原始图像经过像素值处理，得到二进制比特流，传入OTFS-IM 系统中。OTFS-IM 系统如图1 所示。假设一个完整的OTFS-IM 帧中，子载波数为M，符号数为N，总带宽为MΔf，Δf是子载波频率。共有二进制B比特流信息被平均分成G组，每组有b=B/G比特被映射到OTFS 的子块中。每个OTFS子块中的符号长度为n=MN/G，选择其中k个数据点作为传输星座符号，n-k个数据点处于静默位置（即默认传输的数据为0）；每个组中b比特由DD 域索引比特b1和符号比特b2组成。b1比特被用来选择索引位置，b2比特则用于选择发射的星座符号。

图1 OTFS-IM 系统框图

在IM 调制之前，第β个子块的索引选择表示为

式中：iβ,γ∈{1,…,n}，β={1,…,G}，γ={1,…,k}。剩下的b2比特选择发射的星座符号表示为

式中：sβ(γ)∈Q，β和γ的取值与式相同，Q 表示调制后的星座符号集合。

本文采用的索引选择方案是查表法，参数采用文献[7]中的参数，当n=4，k=2 时，所有的激活方案共有C42=6 种组合，但是采用2 比特信息作为索引比特长度，只能选择22=4 种激活组合，会产生其他两种无效的索引组合{1，3}、{2，4}，对检测信号产生干扰。

因此，第β个子块的实际DD 域传输表示为

其他子块也执行相同的操作，实际的OTFS-IM信号表示为

1.2 OTFS 调制解调

对信号x处理，得到DD 域发送符号Xdd∈CM×N，首先经过逆辛有限傅里叶变换（Inverse Symplecticfinite Fourier Transform，ISFFT）将DD 域信号转化为时频（Time-Frequency，TF）域信号Xtf为

式中：FM是M×M的归一化离散傅立叶变换矩阵，(·)H为共轭转置运算。

然后通过海森堡变换生成时域信号，表达式为

式中：在矩形脉冲整形中有Gtx=IM。时域信号传输到快时变信道之前需要进行向量化，表达式为

式中：⊗表示克罗内克积运算。经过信道后，接收的时域信号可以表示为

式中：Yt=invec(yt)。Ytf经过辛有限傅立叶变换（Symplecticfinite Fourier Transform， SFFT）得到DD域接收信号为

在DD 域上接收符号和发送符号关联为

式中：y是Ydd的向量化形式，He=(FN⊗IM)Ht是信道矩阵，且w满足均值为0、方差为σ2I的噪声矢量。

2 OTFS-IM 低复杂度算法设计

文献[7]中提出了一种MMSE-ML。MMSE 均衡的目的是得到接近发送向量x的估计值x，能够满足两者之间的均方误差在统计上达到最小，表达式为

式中：ρsnr是DD 域的平均信噪比，y是接收的DD域符号。由于涉及矩阵求逆运算，在硬件实现方面对计算要求较高，不利于实际使用。

2.1 低复杂度的GAMP 算法

由于信道矩阵具有稀疏性，可以采用信道矩阵的稀疏性来进行信号检测。消息传递（Message Passing，MP）算法能够实现优异的性能，但是其复杂度过高仍然不能够直接使用[10]。在信号检测问题中，发送向量x的先验概率密度为px，接收符号向量y是服从p(y|x)=p(y|Hex)的似然函数，其中v=Hex是无噪声形式的线性变换输出。信号检测是为了从已知的接受向量y和信道矩阵He中恢复出发送向量x，若采用最小化条件期望来进行建模，可表示为

分析可知，由于计算px|y(x|y)处理难度大，造成算法复杂度较高。传统的MP 算法通过在因子图的变量节点和观测节点之间迭代更新来传递消息，从而求出px|y(x|y)。虽然MP 算法的性能较优，但是该算法的因子图中需要传递的消息数量更多，复杂度仍然很高。

由于MP 算法复杂度高，文献[11] 提出了GAMP 算法。针对MP 算法的干扰项，GAMP 算法将其近似为高斯随机变量，应用泰勒展开做了近似，从而降低算法的复杂度。GAMP 算法消息传递也采用因子图进行计算。不同于MP 算法中的观测节点y，这里的观测节点是px|v(y|Hex)，x仍然是因子图中的变量节点。

虽然GAMP 算法能够降低复杂度，但是快时变信道的信道矩阵不服从独立同分布，所以存在收敛性问题。为了解决GAMP 的收敛性，文献[9]证明，当阻尼因子数目足够多时，收敛性可以得到保证。

2.2 改进的阻尼因子GAMP 算法

在式（11）的基础上，本文采用的检测算法是采用4 个阻尼因子的GAMP 算法，输入是信道矩阵He、接受向量y，最大迭代次数T，流程如下。

步骤1：初始化。设置迭代序号t=1，初始化xj的均值和方差τjx(t)：，τjx(t)=1。

步骤2：对每个i=1,…,2MN，设置s^(0)=0，计算vi的近似均值和方差τip(t)。

步骤3：令yi的似然函数对每一个i，计算Gi的导数和二阶导数τis，计算公式为

步骤4：令rj=xj+表示含有高斯白噪声的xj，均值为0，方差为τjr。对每个j，计算rj的均值和方差τjr(t)。

步骤5：更新和τjx(t)。对每个j，计算

式中：pc(t) 是第t次迭代的符号sc(t) 的概率，C=|Q|。在发送端，pc(t)的更新公式为

步骤6：更新迭代，令t=t+1，返回步骤2 进行下一次迭代，直到达到预先设置的最大迭代次数T次。

改进的GAMP 算法通过阻尼因子ξs、ξx、ξt以及ξp对s、x^、τx和pc四个变量加权计算，同时控制更新。阻尼因子选择合理，便能够提高GAMP 算法的收敛性。

2.3 基于概率排序的阻尼GAMP 算法

OTFS-IM 方案不同于OTFS 方案，发送向量x中存在着0 符号，其余部分为星座符号。接收端在GAMP 检测时，需要在变量节点x中添加0 元素，变量节点的取值集合Ω∈{0 ∪Q}。本文提出了一种概率排序的补偿措施，以确保检测端获得正确的激活数目[12]。具体方案是在使用GAMP进行迭代后，在进行数据符号判决之前，考虑子块的激活数目是否正确，并对每个数据符号进行判决。

式中：Pc(aj)表示一帧中第c个数据符号判决为aj的概率，可以通过式（21）迭代完成后计算得到。在判决第β个子块中n个数据符号取值的概率分布为{{Pc[Xβ(i)=aj,aj∈Q]},Pc[Xβ(i)=0]},i∈{1,…,n} （23）式中：Xβ(i)表示第β个子块中的第i个数据符号，{Pc[Xβ(i)=aj,aj∈Q]}、Pc[Xβ(i)=0]分别表示第β个子块中的第i个数据符号判决为aj和0 的概率。概率排序的补偿第1 步就是先计算出子块中每个数据符号所有取值为星座符号的概率分布占总体的比值，第i个数据符号取值为星座符号aj的概率的比重表示为

全部计算当前子块中n个数据符号后，第2 步是对每个数据符号取值为星座符号的比重进行排序，第β个子块第i个数据符号的所有取值的排序情况为

第3 步是比较子块中n个数据符号比重进行排序，取前k个最大值作为激活的数据符号。这保证了激活索引的数量正确，提升了系统的性能。

最后，得到检测后的信息比特，进行比特合并，恢复出原始图像。

3 仿真结果及分析

本章目的是评估基于概率排序的GAMP 算法的BER 性能，在相同的条件下与基于概率排序的MP 和MMSE-ML 算法进行比较。在图像传输过程中，模拟了5 条路径，调制方式采用4QAM，载波频率为4 GHz，子载波间隔设为15 kHz，最大速度设置为600 km·h-1，M=64，N=16，n=4，k=1。如图2所示，基于概率排序的阻尼GAMP 算法与基于概率排序的MP 算法性能相差不大，相比于MMSE-ML算法有明显的性能提升。

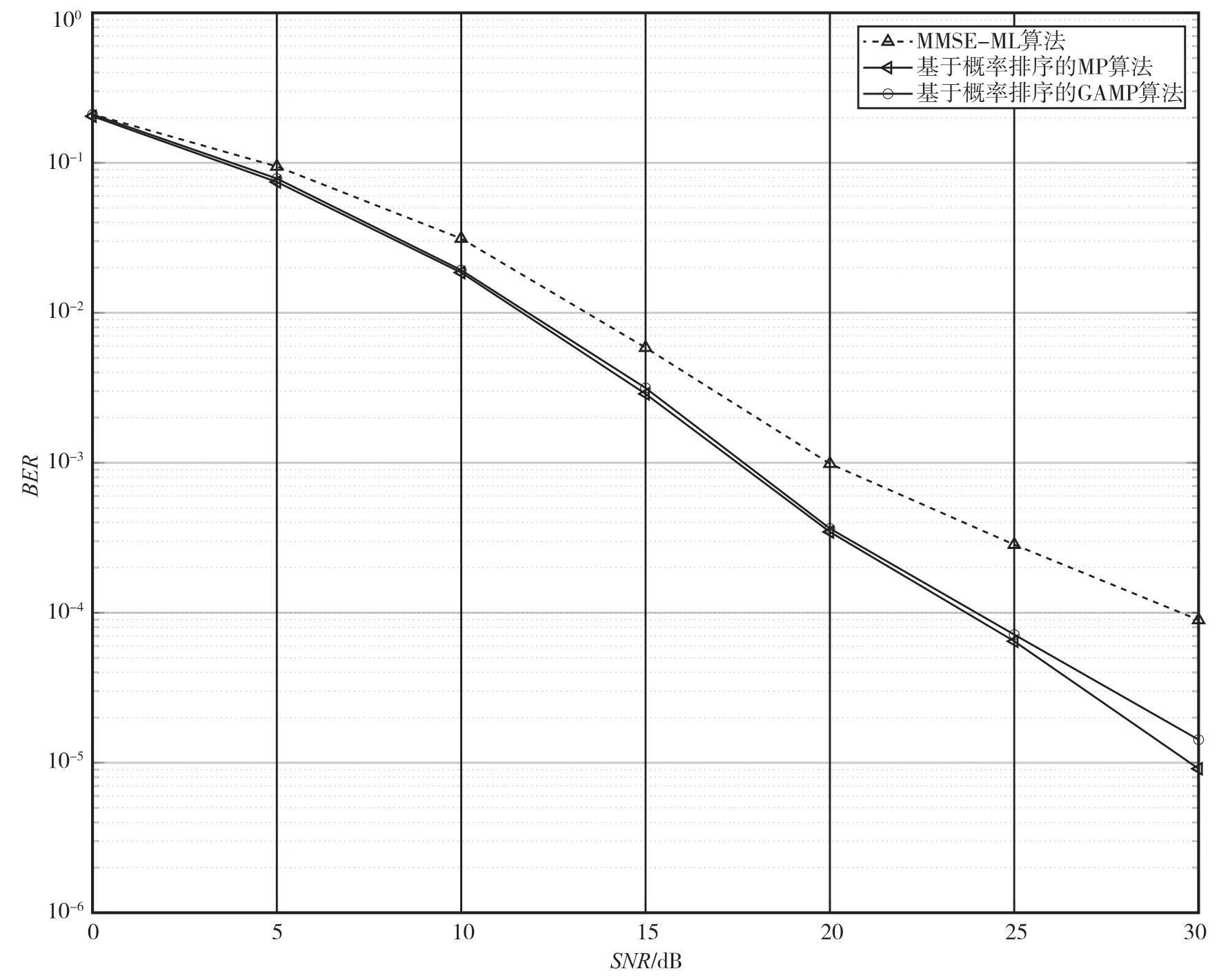
图2 不同算法的误码率表现

SNR=20 dB 时，OTFS-IM 系统的图像如图3所示，BER=0.000 35。

图3 OTFS-IM 系统的发送图像和恢复图像对比

对这几种常见的算法进行比较。MMSEML 的计算复杂度为o[(MN)3]，MP 算法复杂度是o(NMP|Q|T)，其中|Q|表示星座符号的个数，T表示迭代的次数，阻尼GAMP 算法的计算复杂度是o(NMPT)。结合图3 可知，基于概率排序的阻尼GAMP 算法相比于其他算法在计算复杂度上有着明显的优势。

4 结语

针对图像传输中OTFS-IM 的算法复杂度过高问题，本文在阻尼GAMP 算法的基础上提出了一种基于概率排序的阻尼GAMP 算法，降低了算法的复杂度。对于概率排序的阻尼GAMP 算法可以有效地防止接收端检测出现判决索引数目出错的情况，进而提升了系统的误码率性能。仿真结果表明，本文提出的基于概率排序的阻尼GAMP 算法在相对OTFS-IM 系统有一定的优势，更适用于图像传输方向的应用。