含裂隙储层模型数值模拟对比分析

李美琦

（广东省建设工程质量安全检测总站有限公司，广州 510000）

0 引言

地层介质中，孔隙作为一种储存空间，是油气资源运移或者扩散的重要通道，控制油气资源的产能。

深部介质受到上覆介质的压力，水平或者接近水平的裂隙空间被压实，高角度或者垂直的裂隙空间得到保留，HTI 模型是与高角度裂隙特别是垂直裂隙相适应的等效地质模型。含裂隙岩石模型的发展大致经历了建立含裂隙储层模型、建立含裂隙储层模型的理论基础、含裂隙储层数值模拟3 个阶段。

第一阶段，韩媛媛[1]对Eshelby 等效介质模型进行了综合论述和模型建立（如图1 所示）。

图1 Eshelby等效介质模型

图2 研究路线图

第二阶段，在各向同性介质的背景下，加入单一结构裂隙（如定向排列的垂直或平行裂隙）和多元结构裂隙（如同时存在多个单一结构的裂隙系统），但各向同性的背景在实际地质应用中不占优势，对各向异性背景的研究更有价值[2]。

第三阶段，用数值模拟方法研究各种含裂隙模型的响应特征和适用范围[3]，常见的数值模拟方法有波动方程法和有限差分法[4]。熊晓军等[5]用三维波动方程对缝洞地质模型进行了数值模拟。

本文采用波动方程方法对Hudson 模型和Cheng 模型进行数值模拟，比较、分析模型的优、缺点及适用范围，为研究含裂隙储层AVO 响应特征提供模型参考。

1 裂隙储层等效模型分析

1.1 Hudson 模型

Hudson[6-7]用椭球状裂隙近似模拟岩石介质中的扁平状裂隙，发展了含裂隙介质中的弹性波场理论。

Hudson 模型的假设有4 点。第一，弹性波的波长远大于定向排列的裂隙尺度。第二，裂隙分布稀疏、均匀，裂隙所占比重小。第三，裂隙分布不连续，每一个椭球状的裂隙彼此独立。第四，裂隙厚度超过裂隙长度。

对于具有三轴对称的横向各向同性材料，弹性刚度张量由c11、c13、c33、c44、c665 个独立的弹性常数表示：

其中，c12=c11-2c66。

在Hudson 的论著中，利用二阶扩展的等效模量研究介质中裂隙引起的横向各向同性介质方法：

一阶更正量：

二阶更正量：

其中，λ、μ为拉梅常数，ε为裂隙密度，ε与孔隙度(φ)、裂隙纵横比（α）的关系如下：

式（6）中U1、U3由裂隙包含物决定。对于液体填充的裂隙，Hudson 给出了如下U1、U3表达式：

该式子假设流体饱和度不影响介质的压缩模量，即裂隙纵横比α为0。对于干燥裂隙，U1、U3：

在式（8）、(9)中，裂隙纵横比为0。

Hudson 给出了对于“弱”包含物U1、U3的表达式：

其中，K'为包含物的体积模量，μ'为包含物的剪切模量。

根据Hudson 模型理论基础，可获得Hudson 模型中弹性刚度张量的独立弹性常数与裂隙密度之间的关系。c13、c66对裂隙密度变化的响应十分微弱，本文仅对c11、c33、c44进行数值模拟、分析。

在岩石物理研究中，通过纵波速度（Vp）、横波速度（Vs）、介质密度（ρ）建立岩石介质模型，进行数值模拟：

本文Hudson 模型参数见表1，裂隙密度变化范围从0 ～0.5，裂隙类型为干燥裂隙和液体填充裂隙。计算结果经标准化、归一化，所有的数据在相同的尺度（0 ～1）内，由此得到的量称为标准化等效模量。

表1 Hudson模型参数

图3 为Hudson 模型正演模拟结果。图3（a）为干燥裂隙一阶更正标准化等效模量与ρ的关系曲线，随着ρ的增加，等效模量线性减小，c11、c3、c4分别在ρ为0.56、0.23、0.51 处取0。

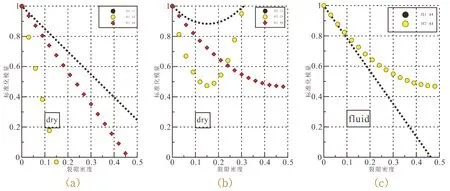
图3 Hudson模型正演模拟结果

图3（b）为干燥裂隙二阶更正标准化模量与ρ的关系，呈非线性关系，等效模量先减小再增加，c11、c3、c4分别在ρ为0.18、0.18、0.42 处取得最小值。

图3（c）为液体填充一阶、二阶更正标准化等效模量与ρ的关系。液体填充情况下c11、c3恒等于1.0。液体填充后，一阶c44与ρ依旧呈线性关系，在0.46 处为零，ρ继续增加，其将会小于零；二阶c44与ρ呈非线性关系，先减小后增加，在ρ在0.52 处取得最小值。

1.2 Cheng 模型

Cheng[8]在Hudson 模型的基础上提出了新的二阶扩展的各向异性模型，即Cheng 模型。Cheng 模型使用与Hudson 模型一样的物理模型。

将球状包含物的精确解和Padé 近似扩展，其等效弹性模量：

将Hudson 模型中关于裂隙密度ε的一阶、二阶更正量用Padé 近似系数表示：

图4 为Cheng 模型正演模拟结果。图4（a）为干燥裂隙环境下Cheng 模型标准化等效模量与ε的关系。曲线呈现非线性关系，随着ε的增加，标准化等效模量单调减小；在研究裂隙范围内，未出现最小值及反向增加情况。

图4 Cheng模型正演模拟结果

图4（b）为液体填充下Cheng 模型的标准化等效模量与ε的关系。液体填充情况下c11、c33近似，标准化模量值恒等于1.0。标准化模量与ε呈非线性关系，随着ε的增加，标准化等效模量非线性减小，在研究范围内，未出现最小值及反转增加情况。

1.3 模型对比

对Hudson 模型与Cheng 模型分别进行了干燥裂隙、液体填充裂隙的数值模拟，分别得到c11、c33、c44随裂隙密度的变化规律，比较这两种模型的优点、不足和适用范围。

图5 中（a）、（b）、（c）为干燥型裂隙中Hudson 模型的一阶更正、二阶更正和Cheng 模型拟合更正结果，分别对应c11、c33、c44的标准化模量随裂隙密度ε的变化规律。图5（d）图为液体填充型裂隙中c44随裂隙密度变化的Hudson 模型一阶更正、二阶更正、Cheng 模型拟合更正曲线。

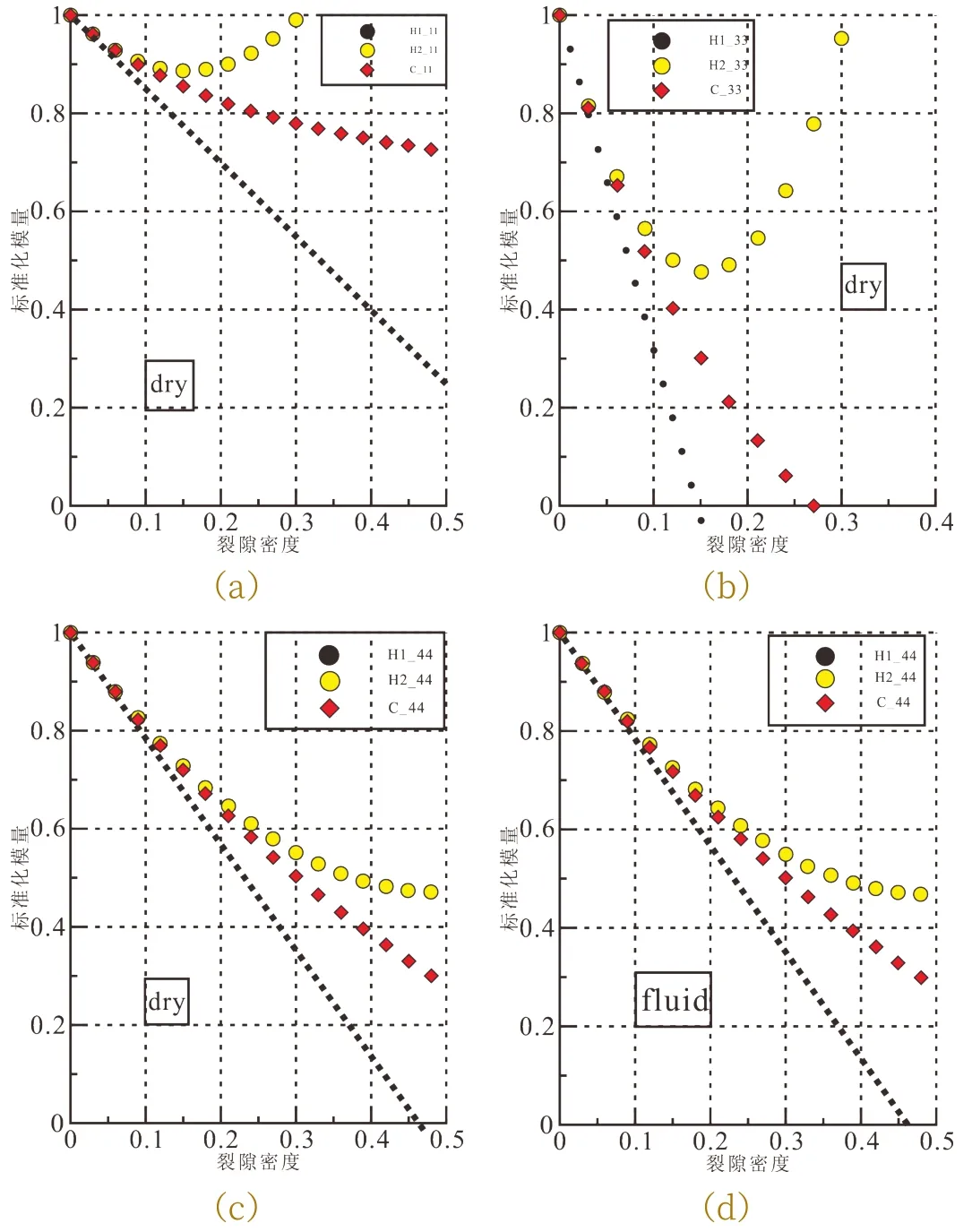
图5 Hudson模型与Cheng模型数值模拟对比

对比可知，Hudson 模型一阶更正和二阶更正表现出明显的局限性，仅在极小裂隙密度范围内具有良好的表现。Hudson 模型一阶更正与裂隙密度呈线性递减，标准化模量对模型参数的改变不敏感，难以刻画参数的微妙变化；Hudson 二阶更正出现标准化模量增加的现象，不符合实际物理模型弹性参数变化规律。Cheng 模型标准化等效模量随裂隙密度的变化具收敛性，不随裂隙密度的增加而无限减小，Cheng 模型的数学过程严谨，对参数变化的响应敏感；可以适应更广泛的裂隙密度，能够满足实际情况的需求。

2 结论

通过对Hudson 模型和Cheng 模型的模拟、对比、分析，得到以下结论。

（1）Cheng 模型拟合更正曲线落在Hudson 一阶更正曲线和二阶更正曲线之间，表明Cheng 模型适应的地层裂隙密度范围比Hudson 模型的更广，能适应实际情况中较大的裂隙密度数值。

（2）Cheng 模型中弹性常数随裂隙密度的增长具有一定的收敛性，合理地解决了二阶扩展的越界问题，能与实际物理原理相适应；Cheng 模型采用Padé 近似拟合的系数由Hudson 模型数学方法计算得到，在数理上Cheng 模型拟合更正与Hudson 模型二阶扩展同样有效，且计算性能更优越。