干式空心电抗器应变检测方法及低温条件下应变特性

赵春明， 冷 俊， 杨晶莹， 王永红， 庄 羽，于群英， 杨代勇， 李守学， 翟冠强

（1.国网吉林省电力有限公司电力科学研究院，吉林 长春 130021；2.哈尔滨理工大学 电气与电子工程学院，黑龙江 哈尔滨 150080）

0 引 言

干式空心电抗器是电网中常用的无功设备，近些年一直有较高的故障率，多数故障是因匝间绝缘缺陷击穿造成匝间短路[1-2]。近几年通过开展匝间过电压现场试验，查找出具有缺陷的干式空心电抗器，在运行过程中烧毁故障率明显降低[3-4]。虽然现场试验能够发现缺陷电抗器，但是不能从根本上解决存在匝间绝缘缺陷的问题。因此，干式空心电抗器一直面临着运行年限较低的问题[5]。

包封绝缘开裂是造成干式空心电抗器烧毁的主要原因之一[6-7]。在过电压、受潮和脏污等条件下，开裂位置发生局部放电逐渐破坏匝间绝缘，最终引起匝间短路，导致电抗器烧毁。在寒冷地区，干式空心电抗器在低温下运行，包封绝缘开裂尤其严重[8]。

一般认为包封绝缘开裂原因包括电动力破坏和热应力破坏。并联电抗器产生的电动力较小，压强不足以破坏绝缘[9]。由于并联电抗器包封绝缘经常发生开裂，可以确定热应力是导致绝缘开裂的主要原因。投入电抗器时温度会逐渐升高，切出运行电抗器时温度逐渐下降，由于包封内部铝导线、聚酯薄膜绝缘和环氧玻璃丝绝缘材料的热膨胀系数不同，投入和切出电抗器时温度骤变会产生热应力，导致实际运行的干式空心电抗器经常出现异常响动[10]。因此，研究降温和通流过程包封内部产生的热应力对包封绝缘的破坏性具有工程实际意义。

在热力学方面，针对干式空心电抗器温升和温度场分布等问题，国内外学者开展了大量的仿真和试验研究，获得了比较成熟的制造经验[11-13]。而针对热应力破坏问题研究较少，比较典型的研究成果包括：徐可新等[14]针对空心电抗器包封应变和应力进行仿真，认为微裂纹存在使包封绝缘材料上的应力集中导致包封绝缘开裂；周延辉等[15-16]利用光纤Bragg光栅传感技术，对干式空心电抗器固化和温升试验过程的温度和应变变化特性进行了测量，检测到固化和升温过程包封内部均出现负应变。现有的研究成果还不能说明在低温运行条件下的热应力是导致干式空心电抗器包封绝缘开裂的主要原因。

为了探索包封绝缘在低温运行条件下的开裂成因，本文对包封绝缘应变测量方法开展研究，制作干式空心电抗器试验模型，搭建试验系统，在低温条件下测试降温和通流过程包封绝缘的温度、轴向应变和周向应变，并根据应变试验结果，讨论热应力的破坏性。

1 试验模型制作及应变测试方法

1.1 试验模型制作方法

1.1.1 试验模型尺寸确定方法

干式空心电抗器普遍采用多包封、多线圈并绕结构。每个包封内部一般有2～6层线圈，外部缠绕环氧玻璃丝绝缘，包封间通过撑条支撑形成气道加强散热，各包封两端与星形架连接，通过高温固化形成一个整体。干式空心电抗器具有较大的几何尺寸，以一台GKBK-20000/66型干式空心并联电抗器为例，其直径和高度均达到3 m。如果按照它的尺寸制作试验模型，试验开展非常困难，试验模型需要小型化。

将干式空心电抗器包封内部结构分成内绝缘、线圈和外绝缘3部分，如图1所示。内绝缘的内、外半径分别为R1和R2，外绝缘的内、外半径分别为R3和R4。设包封内外绝缘厚度相等，绝缘厚度δ1和线圈厚度δ2分别如式（1）～（2）所示。

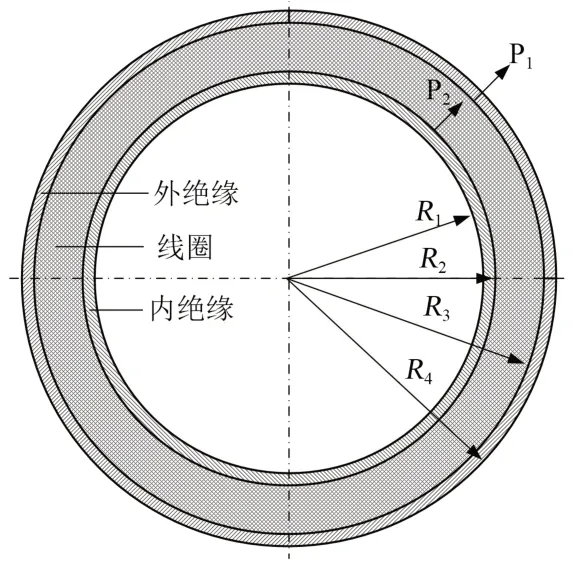
图1 包封内部结构Fig.1 The internal structure of encapsulate

对于干式空心电抗器，包封厚度约为20 mm，绝缘厚度和线圈厚度满足式（3）。在力学上包封属于薄壁管，周向应力远大于径向应力，径向应力可以忽略。

假设线圈处于热膨胀状态，外绝缘内侧承受线圈施加的压力P1方向向外，内绝缘外侧承受线圈施加的拉力P2方向也向外。

当满足式（3）条件时，忽略内部温差的影响，外绝缘及线圈周向应变与温度的关系如式（4）所示。

式（4）中：εθ1为内绝缘在R=R2处及外绝缘在R=R3处的周向应变；εθ2为上述两个位置线圈的周向应变；E1和E2为绝缘和线圈的弹性模量；μ1和μ2为绝缘和线圈的泊松比；α1和α2为绝缘和线圈的线膨胀系数；T0为初始温度；T为升温后温度。

轴向方向，包封绝缘和线圈相约束，两者长度相等。包封绝缘轴向应变εz1和线圈轴向应变εz2之间的关系如式（5）所示。

当满足式（3）关系时，得到式（4）周向应变与直径大小无关，但与包封绝缘厚度和线圈厚度有关。制作试验模型时，在满足式（3）条件下，包封绝缘的半径可以适当减小，包封内部绝缘厚度和线圈厚度不能改变。式（5）表明轴向应变间的关系与高度无关，可以适当降低试验模型高度。

1.1.2 试验模型线圈绕制方法

干式空心并联电抗器的损耗主要为电阻损耗，涡流损耗和杂散损耗较小。包封内部由多层线圈并绕构成，各层线圈有导线电阻和自感，线圈间有互感。外施电压为U，以4层线圈为例，电压方程如式（6）所示。

式（6）中：ω为角频率；R1～R4为各层线圈的导线电阻；L1～L4为各层线圈的自感；M1,2～M3,4为各层线圈间的互感，I1～I4为流过各层线圈的电流。

所有线圈的总电阻损耗如式（7）所示。

由式（6）可见，各线圈上的电压降包括导线电阻上的压降、自感上的压降和互感的感应势3部分，其中电阻上的压降非常小。要得到式（7）表述的电阻损耗，试验需要非常高的外施电压和电源容量。

如果采用无感绕法，将线圈1和线圈3正绕，线圈2和4反绕，电压方程如式（8）所示。

各线圈自感和互感上的电势相互抵消，如电阻损耗不变，仅需要非常低的外施电压和电源功率进行试验。

1.2 温度传感器和应变片预埋方法

本文选用温度传感器和应变片对测试点温度和应变进行测量。为了预埋方便，温度传感器选用体积较小的PT100型热电阻温度传感器，温度测量范围为-70～500℃，测量准确度为0.1%。应变片选用美国OMEGA公司生产的SGD-7/350-LY13型精密应变片，应变片的长度为7 mm，测量最大值为50 000 με，偏差为±0.3%，使用温度范围为-70～200℃。

应变片的厚度薄且金属丝细，如果制作过程直接埋入试验模型中，包封绝缘缠绕过程容易破坏应变片。本研究首先将温度传感器和应变片固定在厚度为0.18 mm的Nomex410型绝缘薄纸上，再埋入包封绝缘中。

厚度为0.18 mm的Nomex410型绝缘薄纸的拉伸强度为130 MPa，伸长率为0.19%，估算弹性模量为0.7 GPa，而环氧玻璃丝弹性模量为14～45 GPa，说明Nomex比环氧玻璃丝更具有柔软性，两者粘接在一起不会对环氧玻璃丝绝缘产生大的热应力。

1.3 应变计算方法

在没有温差的条件下，如果包封绝缘是自由的，则不会产生热应力。虽然不产生热应力，包封绝缘由于热膨胀也会产生应变。应变必须已知，通过试验模型应变计算过程才能从总应变中求出热应力产生的应变，所以需要先制作一个包封绝缘模型，对包封绝缘热膨胀产生的应变进行测量。

在试验温度范围内取多个测量点，对包封绝缘模型的应变特性进行测量。在任一温度Ti下，轴向应变测量值为εz1,1(Ti)，周向应变测量值为εθ1,1(Ti)，它们具有各自的初始偏量；设20℃条件下轴向应变和周向应变为0，得到包封绝缘模型的轴向应变εz1,2(Ti)和周向应变εθ1,2(Ti)如式（9）～（10）所示。

通过数据拟合得到包封绝缘模型轴向应变和周向应变与温度函数关系，如式（11）～（12）所示。

试验模型长期存放在室温中，可以认为在20℃时热应力产生的应变为0。在降温和通流过程，对每个测试点的温度和应变进行测量，任一温度Tj下测量的轴向应变测量值为εz1,3(Tj)，周向应变测量值为εθ1,3(Tj)，则在热应力作用下，在该温度下包封绝缘轴向应变εz1(Tj)和周向应变εθ1(Tj)计算方法如式（13）～（14）所示。

式（13）和式（14）得到正值代表热应力使绝缘拉伸，负值代表热应力使绝缘压缩。

2 试验条件及试验方法

2.1 试验模型制作

本文试验模型采用1个包封，内部采用4层线圈绕制，第1层与第3层正绕，第2层和第4层反绕。每层线圈3股并绕，电磁线选用膜包圆铝导线，导线直径为3.38 mm，绝缘结构为两层聚酰亚胺、1层聚酯和1层聚酯纤维非织布。包封绝缘选用环氧玻璃丝纤维，玻璃丝纤维比重为70%～75%，沿周向顺玻璃丝缠绕。

试验模型委托北京电力设备总厂加工，绕制和固化加工工艺同GKBK-20000/66型电抗器加工工艺一样。试验模型的主要技术参数如表1所示，同时满足式（3）条件。

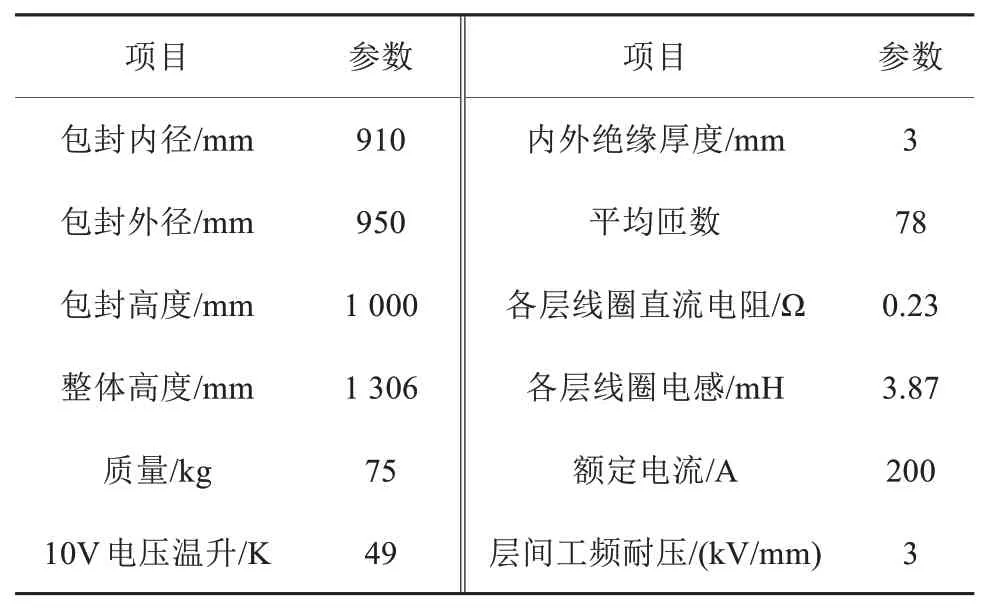
表1 试验模型的主要技术参数Tab.1 Main technical parameters of test model

本研究的温度传感器和应变片采用预埋方式，这种方式具有广泛的适用性。试验模型制作过程中，在线圈和包封外绝缘间，距离底部分别为200 mm（下部）、500 mm（中部）和850 mm（上部）处预埋温度传感器、轴向应变片和周向应变片，实物如图2所示。后续试验发现，仅上部轴向应变片损坏。

图2 温度传感器与应变片预埋方式Fig.2 Temperature sensor and strain gauge embedding method

为了求取自由膨胀包封绝缘的应变，同时制作内径为910 mm、厚度为3 mm、与试验模型包封绝缘材料一致的包封绝缘模型。固化后，在其外表面粘贴轴向和周向测量的应变片，包封绝缘模型如图3所示。

图3 包封绝缘模型Fig.3 Insulation model of encapsulation

2.2 试验设备

试验设备构成如图4所示，包括通流供电系统、低温舱及温度与应变测量系统3部分。

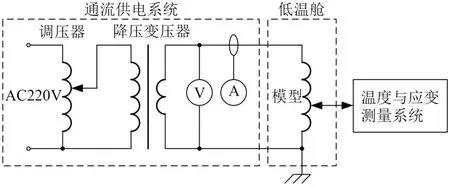
图4 试验设备构成Fig.4 Composition of test equipment

通流供电系统采用交流220 V供电，调压器用于调节输出电压大小，变压器用于降压，电压表和电流表测量输出电压和输出电流。供电系统额定输出电压为50 V，额定电流为800 A，电流测量准确度为1%。低温舱尺寸为2 m×2 m×2.5 m，控制温度范围为-40～120℃，控制精度为±1℃。温度和应变测量系统选用静态电阻应变仪，温度测量范围为-70～500℃，准确度为0.1%；应变测量范围为±20 000 με，准确度为0.2%±2 με；采样频率为0.01～2 Hz，通过计算机显示和存储试验数据。

2.3 试验方法

试验分为降温试验和通流试验，模拟电抗器投切过程温度骤变。

（1）降温试验

在寒冷地区环境温度变化非常大，冬季最低温度可以达到-40℃。试验温度选择-40、-30、-20、-10、0℃，共5个温度点。将试验模型在室温下放置24 h以上后再放入低温舱内，低温舱按照设定温度开始降温，持续3 h达到热稳定。

（2）通流试验

降温过程完成后，保持低温舱温度不变，对试验模型通电流，电流选择200 A，持续3 h达到热稳定。

上述两个试验过程中，按照10 s时间间隔，持续监测并保存试验模型上各测试点的温度和应变量。

3 结果与分析

3.1 应变校验

3.1.1 包封绝缘模型应变特性

将包封绝缘模型放置到低温舱内，温度范围为-40～120℃，间隔20℃，各温度点下持续放置3 h后进行轴向应变和周向应变测试，按照式（9）和式（10）计算应变值，结果如图5所示。从图5可以看出，随温度升高，包封绝缘轴向应变和周向应变均逐渐增加。数值上轴向应变大于周向应变，存在各向异性特征。轴向应变与温度成线性关系，周向应变与温度为非线性关系。

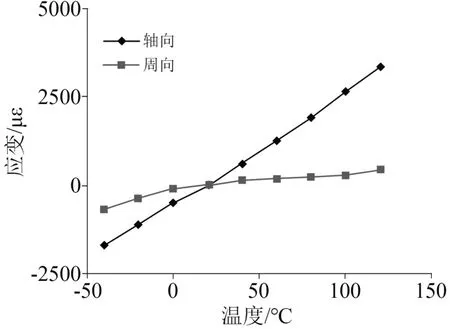
图5 包封绝缘模型应变-温度特性Fig.5 Strain-temperature characteristics of encapsulated insulation model

拟合图5结果，得到包封绝缘应变与温度函数关系如式（15）～（16）所示。

以上两式中温度变量的系数为线膨胀系数，单位为10-6℃-1，常数项的单位为με。

常温下玻璃丝和环氧树脂的线膨胀系数如表2所示。从表2可以看出，玻璃丝的线膨胀系数远小于环氧树脂的线膨胀系数[17]。

表2 玻璃丝和环氧树脂绝缘的线膨胀系数Tab.2 Linear expansion coefficient of glass fiber and epoxy resin insulation

温度高于0℃时，包封绝缘的轴向线膨胀系数为31.2×10-6℃-1，周向线膨胀系数为4.58×10-6℃-1，轴向线膨胀系数远大于周向线膨胀系数。包封绝缘的轴向线膨胀系数约为环氧树脂的55%，周向线膨胀系数与无碱玻璃丝的线膨胀系数相差不大，说明玻璃丝受力有取向性。温度低于0℃时，包封绝缘轴向线膨胀系数与常温时保持不变，周向线膨胀系数增加到14.8×10-6℃-1，，收缩时玻璃丝的取向减弱。

3.1.2 对比试验

为了验证预埋应变片测量的有效性，在试验模型外表面粘贴温度传感器、轴向和周向应变片，实物如图6所示，在室温下对试验模型通流200 A开展对比试验。按照式（13）和式（14）计算应变值，结果如图7所示。从图7可以看出，轴向应变为负值，随温度成线性下降；周向应变为正值，随温度成线性上升；周向应变大于轴向应变。应变由包封绝缘和线圈线膨胀系数决定，线圈主要为铝合金材料，其线膨胀系数为23×10-6℃-1，包封绝缘周向线膨胀系数小于线圈线膨胀系数，应变为正值；包封绝缘轴向线膨胀系数大于线圈线膨胀系数，应变为负值。试验结果与理论结果相一致。预埋的应变片与外侧新粘贴应变片测量的应变随温度变化规律一致，证明预埋应变片测量结果可信。应变测量结果具有较小分散性，这是因为试验模型采用手工绕制且不同位置存在一些结构差异。

图6 试验模型外表面粘贴应变片和温度传感器Fig.6 Strain sensor and temperature sensor pasted on the outer surface of test model

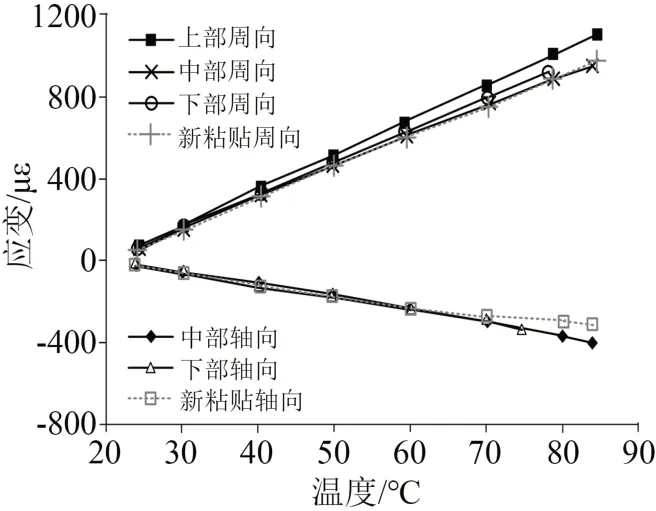
图7 对比试验结果Fig.7 Contrastive test results

3.2 应变试验结果

3.2.1 降温和通流过程温度变化

以试验温度为-40℃为例，降温及通流过程各测试点温度变化如图8所示。从图8可以看出，低温仓的降温速度接近2℃/min，降温过程各测试点温度缓慢下降，变化率先增大后减小，进入稳态需要2～3 h。降温完成后通流200 A，各测试点温度缓慢上升，变化率逐渐减小，进入稳态需要2 h左右，温升接近50 K。由于试验模型仅有单个包封且在低温仓上部、中部和下部的温升差异较小，温度特性满足热力学规律，与工程实践升温过程也一致，在此不再赘述。

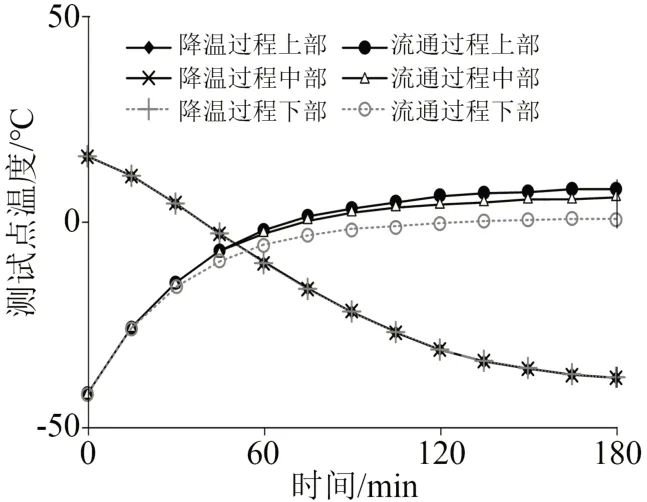
图8 降温与通流过程温度变化Fig.8 Temperature change during cooling and applying current

3.2.2 降温试验应变结果

不同舱温下，降温试验周向和轴向应变与温度的关系如图9所示。从图9可以看出，周向应变和轴向应变随温度降低变化规律存在较大差异。不同舱温下任一周向应变均为负值。周向应变随温度降低逐渐下降，同一舱温下的下降速度逐渐变缓，不同舱温下随温度降幅增加周向应变数值明显增大。这一规律与包封绝缘周向线膨胀系数小于线圈线膨胀系数相对应，也与应变和温度变化速度正相关相对应。舱温较高时轴向应变为正值，随温度降低逐渐转变成负值，轴向应变变化规律从随温度降低逐渐上升转化为逐渐下降。包封绝缘轴向线膨胀系数大于线圈线膨胀系数，降温过程中轴向应变应该为正值，并且随温度降低应变逐渐上升，但是随舱温降低，轴向应变极性和变化规律发生改变，原因是周向应变影响了轴向应变：周向应变大于轴向应变，周向压缩力造成绝缘轴向拉伸，降温过程绝缘轴向收缩量小于线圈的轴向收缩量，应变转化成负极性。

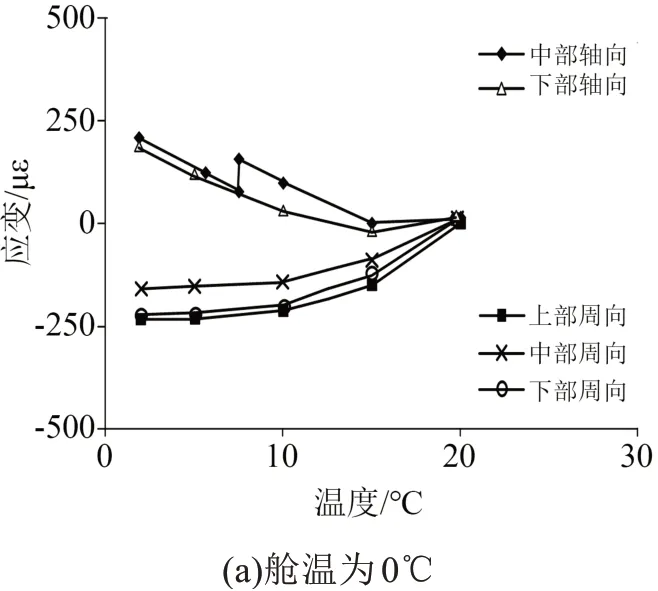
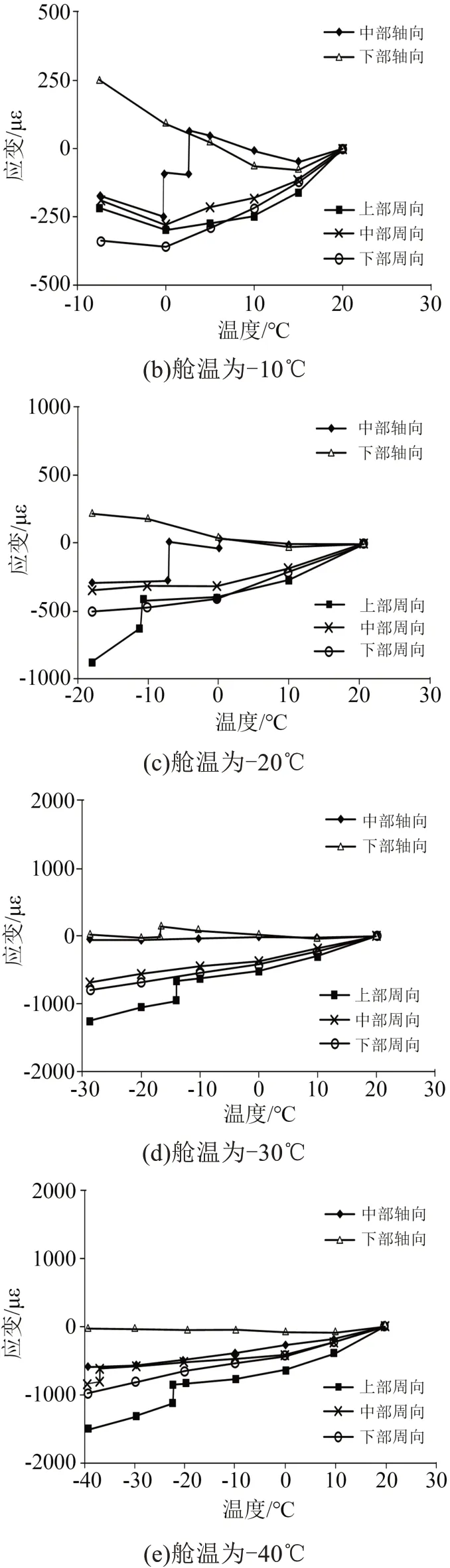
图9 降温过程应变-温度特性Fig.9 Strain-temperature characteristics of cooling process

降温过程轴向应变和周向应变多次出现负跳变，中部轴向应变和上部周向应变最明显。负跳变不符合热力学基本定律，可能包封绝缘由于压缩力出现收缩微裂纹，应变最大数值接近300 με。

3.2.3 通流试验应变结果

每次降温试验完成后继续进行通流试验，通流过程应变与温度关系如图10所示。从图10可以看出，在通流过程中，周向应变随温度升高成线性规律上升。周向应变上升梯度基本一致，如去除降温过程负跳变产生的分散性，它们的大小也基本一致。轴向应变随温度升高逐渐下降，每次试验随舱温升高伴随着周向应变影响引起的轴向拉伸逐渐变小，所以舱温越低轴向应变下降速度越缓。通流过程，周向应变及轴向应变均没有发生跳变。同时发现，降温过程出现的负跳变不能得到恢复。

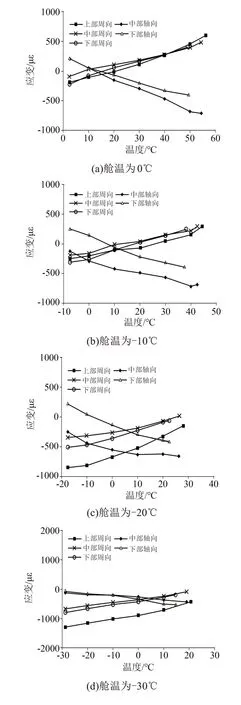
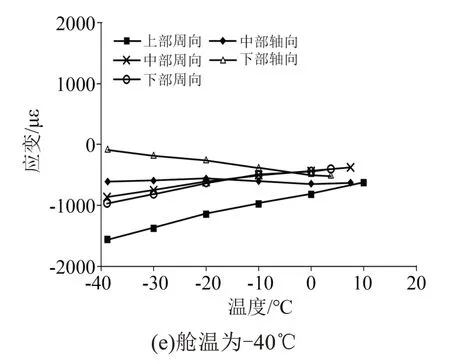
图10 通流过程应变-温度特性Fig.10 Strain-temperature characteristics during applying current

4 应力破坏性分析

工程上对复合绝缘材料强度判定理论包括最大应力理论、最大应变理论、Hill-蔡（SWTsai）强度理论和蔡-吴（EMWu）张量理论等，其中最大应力理论最为常用[17]。

按照热力学基本规律，轴向应力σz1和周向应力σθ1与应变的关系如式（17）所示。

环氧玻璃丝复合材料顺玻璃丝方向（周向）及垂直玻璃丝方向（轴向）的弹性模量、泊松比、拉伸强度和抗压强度特性如表3所示[18-19]。从表3可以看出，周向的单向复合绝缘材料有“抗拉不抗压”特性，轴向的单向复合绝缘有“抗压不抗拉”特性。

表3 环氧玻璃丝的材料特性Tab.3 Properties of epoxy glass fiber material

去除负跳变对最大应变值统计的影响，将多个测试点的最大应变值取算术平均，按照式（17）计算热应力，结果如表4所示，其中正值代表拉伸力，负值代表压缩力。

对比表4和表3发现，仅降温过程周向应力数值超出了周向方向的抗压强度42 MPa，其他值均远小于材料的拉伸强度或抗压强度。降温过程压缩力是造成绝缘开裂的原因，应变负跳变是这一结果的试验表象。

5 结 论

（1）本文探索了干式空心电抗器应变测试用试验模型的制作方法、应变片预埋方法和应变计算方法，通过试验验证了方法的可行性。

（2）实测了低温环境下降温和通流过程包封绝缘周向应变和轴向应变温度特性，发现降温过程出现收缩微裂纹，并通过热应力计算进行验证。包封绝缘周向线膨胀系数远小于线圈线膨胀系数以及周向抗压强度低是造成开裂的原因。增大包封绝缘周向线膨胀系数及提高抗压强度是减少开裂的重要措施。